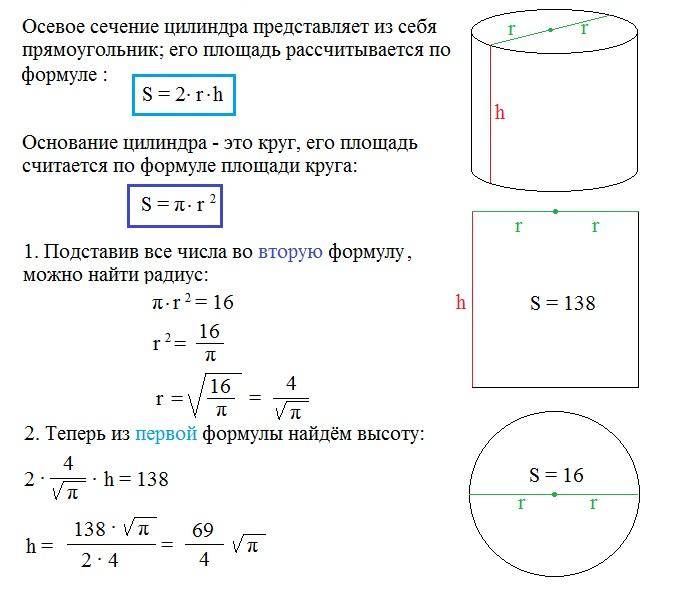
как найти высоту цилиндра,зная площадь сечения и площадь основания!???
Профи
(775),
закрыт
13 лет назад
Дополнен 13 лет назад
вот вся задача…. Площадь осевого сечения цилиндра равна 6 корень из пи, а площадь основания цилиндра равна 25.Найдите высоту цилиндра.
а) 2/3п б) п/2 в) 0,6п г) 2дм ПОМОГИТЕ!! =)
Михаил Зверев
Просветленный
(38577)
13 лет назад
Сечения бывают разные. Если имеется ввиду осевое сечение, то из площади основания можно найти диаметр и это будет одна сторона сечения. А зная одну сторону и площадь прямоугольника, легко найти др. сторону
ltlyfon
Вопрос по геометрии:
Как найти высоту цилиндра, если известна площадь основания и площадь осевого сечения цилиндра
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
kinina147
S cеч = d*h = D*h=2R*h (D- диаметр = d диагонали)
S осн = ПR²
Далее тебе дано основание выражаешь с этой формулы S осн = ПR² радиус
далее
s сеч = 2r*h
тебе дано площадь сечения и радиус подставляешь находишь h
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Как вычислить высоту цилиндра
У цилиндра имеется высота, которая перпендикулярна двум его основаниям. Способ определения ее длины зависит от набора исходных данных. Таковыми могут быть, в частности, диаметр, площадь, диагональ сечения.

Инструкция
Для любых фигур существует такой термин, как высота. Высотой обычно называется измеряемая величина какой -либо фигуры в вертикальном положении. У цилиндра высота -это линия, перпендикулярная двум его параллельным основаниям. Также у него есть образующая. Образующая цилиндра -это линия, вращением которой получается цилиндр. Она, в отличие от образующей других фигур, например конуса, совпадает с высотой.
Рассмотрим формулу, с помощью которой можно найти высоту:
V=πR^2*H, где R – радиус основания цилиндра, H – искомая высота.
Если вместо радиуса дан диаметр, данная формула видоизменяется следующим образом:
V=πR^2*H=1/4πD^2*H
Соответственно, высота цилиндра равна:
H=V/πR^2=4V/D^2
Также высоту можно определить, исходя из диаметра и площади цилиндра. Существует площадь боковой и площадь полной поверхности цилиндра. Часть поверхности цилиндра, ограниченная цилиндрической поверхностью, называют боковой поверхностью цилиндра. Площадь полной поверхности цилиндра включает в себя и площадь его оснований.
Площадь боковой поверхности цилиндра вычисляется по следующей формуле:
S=2πRH
Преобразовав данное выражение, найдите высоту:
H=S/2πR
Если дана площадь полной поверхности цилиндра, вычисляйте высоту несколько иным способом. Площадь полной поверхности цилиндра равна:
S=2πR(H+R)
Вначале преобразуйте данную формулу как показано ниже:
S=2πRH+2πR
Затем найдите высоту:
H=S-2πR/2πR
Через цилиндр можно провести прямоугольное сечение. Ширина этого сечения будет совпадать с диаметрами оснований, а длина – с образующими фигуры, которые равны высоте. Если провести через это сечение диагональ, то можно легко заметить, что образуется прямоугольный треугольник. В данном случае диагональ является гипотенузой треугольника, катет -диаметром, а второй катет- высотой и образующей цилиндра. Тогда высоту можно найти по теореме Пифагора:
b^2 =sqrt (c^2 -a^2)
Источники:
- Как вычислить объем цилиндра?
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти радиус основания цилиндра: формула через объем, площадь
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение радиуса цилиндра: формула и примеры
В данной публикации мы рассмотрим, как можно вычислить радиус цилиндра и разберем примеры решения задач для закрепления материала.
-
Формулы вычисления радиуса цилиндра
- 1. Через объем и высоту
- 2. Через площадь боковой поверхности
- 3. Через полную площадь поверхности
- Примеры задач
Формулы вычисления радиуса цилиндра
1. Через объем и высоту
Радиус цилиндра рассчитывается по формуле:
V – объем цилиндра; считается как произведение числа π на высоту фигуры на квадрат радиуса круга, являющего ее основанием.
V = πR2h
- R – радиус основания цилиндра, т.е. окружности;
- π – число, округленное значение которого равняется 3,14.
2. Через площадь боковой поверхности
Радиус цилиндра считается таким образом:
Sбок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2πR), являющейся основанием фигуры, на его высоту:
S = 2πRh
3. Через полную площадь поверхности
Радиус цилиндра равен:
Данная формула получена следующим образом:
S – полная площадь поверхности фигуры, равная:
S = 2πRh + 2πR2 или S = 2πR(h + R)
Возьмем первое выражение. Если перенести S в правую часть, получим:
2πR2 + 2πRh – S = 0
Можно заметить, что это квадратное уравнение вида ax2 + bx + c = 0, где:
- a = 2π
- b = 2πh
- c = -S
R является корнем данного уравнения (
x).
* в нашем случае – только один положительный корень, т.к. радиус не может быть отрицательным.
Примеры задач
Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см3. Вычислите его радиус.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:
Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см2, а высота составляет 7 см.
Решение:
Применим формулу, в которой задействованы заданные величины:
Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см
2, а высота – 10 см.
Решение:
Используем третью формулу для нахождения неизвестной величины:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Формула нахождения полной поверхности цилиндра.

Цилиндр (происходит из греческого языка, от слов «каток», «валик») — это геометрическое тело, которое ограничено снаружи поверхностью, называющейся цилиндрической, и двумя плоскостями. Данные плоскости пересекают поверхность фигуры и являются параллельными друг другу.
Цилиндрическая поверхность — это поверхность, которая получена прямой линии в пространстве. Эти движения таковы, что выделенная точка этой прямой линии совершает движение вдоль кривой плоского типа. Такая прямая линия называется образующей, а кривая линия — направляющей.
Цилиндр состоит из пары оснований и боковой цилиндрической поверхности. Цилиндры бывают нескольких видов:
1. Круговой, прямой цилиндр. У такого цилиндра основания и направляющая перпендикулярны образующей линии, и имеется
2. Наклонный цилиндр. У него угол между образующей линией и основанием не является прямым.
3. Цилиндр иной формы. Гиперболический, эллиптический, параболический и другие.
Площадь цилиндра, а также площадь полной поверхности любого цилиндра находится с помощью сложения площадей оснований этой фигуры и площади боковой поверхности.
Формула, по которой вычисляется полная площадь цилиндра для кругового, прямого цилиндра:
Sp = 2п Rh + 2п R2 = 2п R (h+R).
Площадь боковой поверхности ищется чуть сложнее, чем площадь цилиндра целиком, она вычисляется путем умножения длины образующей линии на периметр сечения, образованного плоскостью, которая перпендикулярна образующей линии.
Данная цилиндра для кругового, прямого цилиндра узнается по развертке этого объекта.
Развертка — это прямоугольник, который имеет высоту h и длину P, которая приравнивается периметру основания.
Отсюда следует, что боковая площадь цилиндра является равной площади развертки и может быть вычислена по данной формуле:
Если взять круговой, прямой цилиндр, то для него:
P = 2п R, а Sb = 2п Rh.
Если цилиндр наклонный, то площадь боковой поверхности должна быть равна произведению длины его образующей линии и периметра сечения, которое перпендикулярно данной образующей линии.
К сожалению, не существует простой формулы для выражения площади боковой поверхности наклонного цилиндра через его высоту и параметры его основания.
Чтобы вычислить цилиндра, необходимо знать несколько фактов. Если сечение своей плоскостью пересекает основания, то такое сечение всегда является прямоугольником. Но эти прямоугольники будут разными, в зависимости от положения сечения. Одна из сторон осевого сечения фигуры, которое перпендикулярно основаниям, равна высоте, а другая — диаметру основания цилиндра. А площадь такого сечения, соответственно, приравнивается произведению одной стороны прямоугольника на другую, перпендикулярную первой, или произведению высоты данной фигуры на диаметр его основания.
Если сечение будет перпендикулярно основаниям фигуры, но не будет проходить через ось вращения, то площадь этого сечения будет равна произведению высоты этого цилиндра и определенной хорды. Чтобы получить хорду, нужно построить окружность у основания цилиндра, провести радиус и отложить на нем расстояние, на котором находится сечение. А от этой точки нужно провести перпендикуляры к радиусу от пересечения с окружностью. Точки пересечения соединяются с центром.
С2 = А2 + В2.
Если сечение не затрагивает основания цилиндра, а сам цилиндр круговой и прямой, то площадь этого сечения находится как площадь окружности.
Площадь окружности равна:
S окр. = 2п R2.
Чтобы найти R, нужно ее длину C разделить на 2п:
R = C 2п, где п — число пи, математическая постоянная, вычисленная для работы с данными окружности и равная 3,14.
Формула радиуса цилиндра:
где V — объем цилиндра, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая).
Формула радиуса цилиндра:
где Sb — площадь боковой поверхности, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где S — площадь полной поверхности, h — высота
Цилиндр – это фигура, состоящая из цилиндрической поверхности и двух окружностей, расположенных параллельно. Расчет площади цилиндра – это задача геометрического раздела математики, которая решается достаточно просто. Существует несколько методов ее решения, которые в результате всегда сводятся к одной формуле.
Как найти площадь цилиндра – правила вычисления
- Чтобы узнать площадь цилиндра, необходимо две площади основания сложить с площадью боковой поверхности: S= Sбок.+ 2Sосн. В более развернутом варианте данная формула выглядит так: S= 2 π rh+ 2 π r2= 2 π r(h+ r).
- Площадь боковой поверхности данного геометрического тела можно высчитать, если известны его высота и радиус окружности, лежащей в основании. В данном случае можно выразить радиус из длины окружности, если она дана. Высота может быть найдена, если в условии задано значение образующей. В этом случае образующая будет равна высоте. Формула боковой поверхности данного тела выглядит так: S= 2 π rh.
- Площадь основания считается по формуле нахождения площади круга: S osn= π r 2 . В некоторых задачах может не даваться радиус, но задаваться длина окружности. С данной формулы радиус выражается достаточно легко. С=2π r, r= С/2π. Нужно также помнить о том, что радиус – это половина диаметра.
- При выполнении всех этих расчетов число π обычно не переводится в 3,14159… Его нужно просто дописывать рядом с числовым значением, которое было получено в результате проведения вычислений.
- Далее необходимо лишь умножить найденную площадь основания на 2 и прибавить к полученному числу вычисленную площадь боковой поверхности фигуры.
- Если в задаче указывается, что в цилиндре есть осевое сечение и это – прямоугольник, то решение будет немного другим. В таком случае ширина прямоугольника будет являться диаметром окружности, лежащей в основании тела. Длина фигуры будет равна образующей или высоте цилиндра. Необходимо высчитать нужные значения и подставить в уже известную формулу. В данном случае ширину прямоугольника нужно разделить на два, чтобы найти площадь основания. Для нахождения боковой поверхности длина умножается на два радиуса и на число π.
- Можно высчитать площадь данного геометрического тела через его объем. Для этого нужно из формулы V=π r 2 h вывести недостающую величину.
- В вычислении площади цилиндра нет ничего сложного. Нужно только знать формулы и уметь выводить из них величины, необходимые для проведения расчетов.
Представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.
Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:
Пример расчета площади цилиндра мы рассмотрим после того, как узнаем все необходимые формулы. Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить :
Мы помним, что в этих расчетах используется постоянное число Π = 3,1415926, которое рассчитано как соотношение длины окружности к ее диаметру. Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.
Площадь боковой поверхности цилиндра
Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:
А теперь рассмотрим задачу, в которой нам потребуется рассчитать полную площадь цилиндра.
= 4 см, r
= 2 см. Найдем полную площадь цилиндра.
Для начала рассчитаем площадь оснований:
Теперь рассмотрим пример расчета площади боковой поверхности цилиндра. В развернутом виде она представляет прямоугольник. Его площадь рассчитывается по приведенной выше формуле. Подставим в нее все данные:
Полная площадь круга представляет собой сумму двойной площади основания и боковой:
Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета :
Площадь каждого основания цилиндра равна πr
2 , площадь обоих оснований составит 2πr
2 (рис.).
Площадь боковой поверхности цилиндра равна площади прямоугольника, основание которого равно 2πr
, а высота равна высоте цилиндра h
, т.
.
Полная поверхность цилиндра составит: 2πr
2 + 2πrh
= 2πr
(r
+ h
).
За площадь боковой поверхности цилиндра принимается площадь развертки
его боковой поверхности.
Поэтому площадь боковой поверхности прямого кругового цилиндра равна площади соответствующего прямоугольника (рис.) и вычисляется по формуле
S б.ц. = 2πRH, (1)
Если к площади боковой поверхности цилиндра прибавить площади двух его оснований, то получим площадь полной поверхности цилиндра
S полн. =2πRH + 2πR 2 = 2πR (H + R).
Объем прямого цилиндра
Теорема.
Объем прямого цилиндра равен произведению площади его основания на высоту
, т. е.
где Q — площадь основания, а Н — высота цилиндра.
Так как площадь основания цилиндра равна Q, то существуют последовательности описанных и вписанных многоугольников с площадями Q n
и Q’ n
таких, что
(lim_{n rightarrow infty}) Q n
= (lim_{n rightarrow infty}) Q’ n
= Q.
Построим последовательности призм, основаниями которых являются рассмотренные выше описанные и вписанные многоугольники, а боковые ребра параллельны образующей данного цилиндра и имеют длину H. Эти призмы являются описанными и вписанными для данного цилиндра. Их объемы находятся по формулам
V n
= Q n
H и V’ n
= Q’ n
H.
Следовательно,
V= (lim_{n rightarrow infty}) Q n
H = (lim_{n rightarrow infty}) Q’ n
H = QH.
Следствие.
Объем прямого кругового цилиндра вычисляется по формуле
V = π R 2 H
где R — радиус основания, а H — высота цилиндра.
Так как основание кругового цилиндра есть круг радиуса R, то Q = π R 2 , и поэтому
Калькулятор высоты цилиндра
‘ Калькулятор высоты цилиндра ‘ — это бесплатный онлайн-инструмент, который помогает рассчитать высоту цилиндра с заданным радиусом и объемом.
Какова высота цилиндра Калькулятор?
В калькуляторе высоты цилиндра введите значения радиуса и объема, чтобы найти высоту цилиндра за несколько секунд.
Калькулятор высоты цилиндра
ПРИМЕЧАНИЕ: Введите радиус до трех цифр и объем до пяти цифр.
Как пользоваться калькулятором высоты цилиндра?
Следуйте инструкциям ниже, чтобы использовать калькулятор и найти высоту цилиндра:
- Шаг 1: Введите радиус и объем цилиндра в соответствующие поля ввода.
- Шаг 2: Нажмите кнопку «Рассчитать» , чтобы найти высоту цилиндра.
- Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как найти высоту цилиндра?
Чтобы найти высоту цилиндра, нам нужны входные значения радиуса и объема цилиндра. Объем цилиндра — это вместимость цилиндра или мера занимаемого им пространства. Он рассчитывается по формуле πr 2 h , , где r — радиус круглого основания, h — высота цилиндра, а π(Pi) — математическая константа с приблизительным значением 3.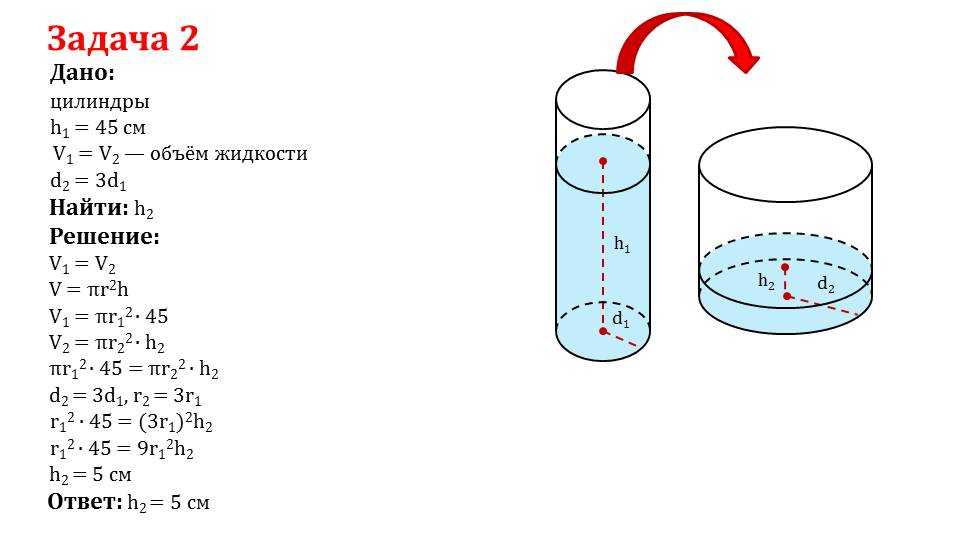
Таким образом, высота цилиндра рассчитывается по формуле V/ πr 2 .
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Решенные примеры расчета высоты цилиндра
Пример 1:
Цилиндр имеет радиус 4 единицы и объем 251,33 кубических единицы. Найдите высоту цилиндра и проверьте ее с помощью калькулятора высоты цилиндра.
Решение:
Формула для нахождения объема цилиндра = πr 2 ч. Радиус = 4 единицы, объем = 251,33 куб. Итак, подставим значения:
Объем цилиндра = πr 2 h
высота цилиндра = V/ πr 2 .
= 251,33 / 3,14 × 4 2
= 251,33 / 50,24
= 5,002 ед.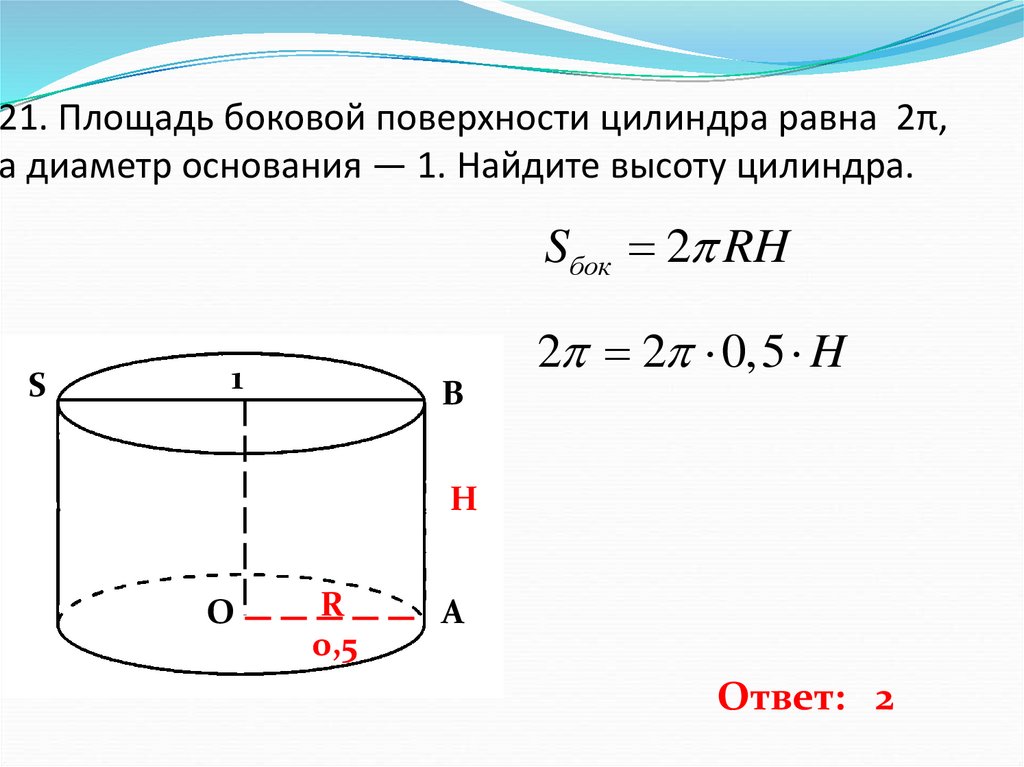
Следовательно, высота цилиндра = 5,002 единицы.
Пример 2:
Цилиндр имеет радиус 7 единиц и объем 300 кубических единиц. Найдите высоту цилиндра и проверьте ее с помощью калькулятора высоты цилиндра.
Решение:
Формула для нахождения объема цилиндра = πr 2 ч. Радиус = 7 единиц, объем = 300 кубических единиц. Итак, подставим значения:
Объем цилиндра = πr 2 h
высота цилиндра = V/ πr 2 .
= 300 / 3,14 × 7 2
= 1,95 ед.
Следовательно, высота цилиндра = 1,95 единицы.
Теперь вы можете попробовать калькулятор высоты цилиндра, чтобы найти высоту цилиндра со следующими размерами:
1) Найдите высоту цилиндра, радиус которого составляет 8 единиц, а объем – 1231,5 кубических единиц.
2) Найдите объем цилиндра, радиус которого 10 единиц, а высота 3455,75 кубических единиц.
☛ Связанные статьи:
- Цилиндр
- Объем цилиндра
☛ Математические калькуляторы:
Объем цилиндра — основы и примеры
00:00:03.
В этом уроке мы узнаем об объеме цилиндра.
00:00:07.090
Начнем, рассмотрим эту окружность радиусом r.
00:00:12.040
К этому моменту мы уже должны знать, что площадь A этого круга равна pi r квадрату.
00:00:18.080
Теперь давайте превратим этот круг в цилиндр.
00:00:22.140
После этого цилиндр имеет радиус r и высоту h.
00:00:29.000
Теперь, чтобы найти объем этого цилиндра V, мы просто умножаем площадь A на высоту h.
00:00:38.100
Следовательно, мы умножаем pi r в квадрате на h.
00:00:43.070
Это дает формулу объема цилиндра, V равно pi r квадрату h.
00:00:51.080
Теперь важно, чтобы мы включили единицу измерения громкости.
00:00:55.170
Поскольку единица измерения не указана, мы можем записать ее как кубическую единицу.
00:01:01.210
Хорошо, давайте рассмотрим несколько примеров нахождения объема цилиндра. Для этих примеров мы принимаем число пи равным 3,14.
00:01:11.200
Найдите объем цилиндра с радиусом 3см и высотой 5см.
00:01:18.140
Начнем с формулы: V равно пи r квадрату h.
00:01:24.040
Теперь, поскольку радиус равен 3 см, мы можем заменить ‘r’ на 3.
00:01:31.140
Теперь упростим 3 квадрата. Здесь мы видим, что 3 в квадрате равняется 3, умноженным на 3. Это дает 9. Давайте запишем это здесь.
00:01:46.180
Продолжим. Высота h равна 5 см. Следовательно, мы можем заменить h на 5.
00:01:54,240
Теперь мы можем упростить это уравнение, умножив 9 на 5. Это даст 45.
00:02:02,220
Далее число пи равно 3,14. Итак, давайте заменим пи на 3,14.
00:02:12.140
Наконец, мы можем найти объем, умножив 3,14 на 45. Это дает 141,30.
00:02:23.110
Обратите внимание, что это число не имеет смысла, если мы не включим для него единицу измерения.
00:02:28.190
Поскольку радиус и высота указаны в сантиметрах, объем будет в кубических сантиметрах.
00:02:34.200
Следовательно, объем этого цилиндра равен 141,30 кубического сантиметра.
00:02:42.130
Следующий пример: объем этого цилиндра составляет 50 кубических футов, а его радиус равен 2 футам. Найдите его высоту, h.
00:02:51.180
Теперь начнем с формулы V = pi r квадрат h.
00:02:57,130
Поскольку объем цилиндра равен 50, мы можем заменить V на 50.
00:03:03,230
Далее, поскольку радиус равен 2, мы можем заменить r на 2
00:03:10.050
Теперь упростим 2 квадрата. 2 квадрат на самом деле, 2 умножить на 2, что равно 4. Давайте запишем это здесь.
00:03:22.120
Далее мы можем заменить пи на 3,14.
00:03:27,120
Здесь мы можем упростить это уравнение, умножив 3,14 на 4.
00:03:33,120
Это дает 12,56.
00:03:36.240
Теперь у нас 12,56 ч равно 50. Давайте перепишем это уравнение, чтобы его было легче увидеть.
00:03:46.230
Затем, чтобы найти «H», мы разделим обе части уравнения на 12,56.
Как найти высоту цилиндра, если известна площадь основания и площадь осевого сечения цилиндра.
Вы перешли к вопросу Как найти высоту цилиндра, если известна площадь основания и площадь осевого сечения цилиндра?. Он относится к категории Геометрия,
для 1 – 4 классов. Здесь размещен ответ по заданным параметрам. Если этот
вариант ответа не полностью вас удовлетворяет, то с помощью автоматического
умного поиска можно найти другие вопросы по этой же теме, в категории
Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном
объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части
сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете
ознакомиться с вариантами ответов пользователей.