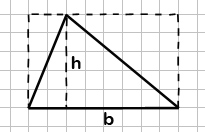
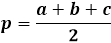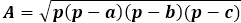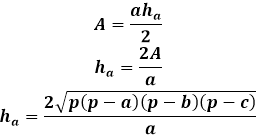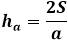Расчёт высоты треугольника по сторонам
Значащих цифр:
Определение треугольника
Треугольник это геометрическая фигура, которая состоит из трёх точек не лежащих на одной прямой и трёх отрезков попарно соединяющих эти точки. У треугольника сумма любых двух длинн сторон должна быть меньше третьей.
Определение высоты треугольника
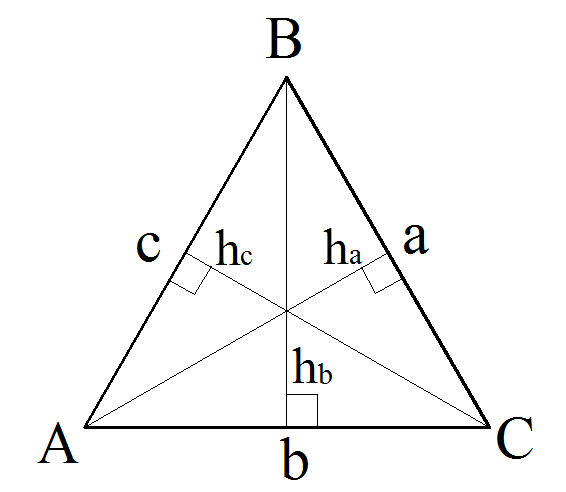
Высота треугольника это перпендикуляр опущенный с вершины на противоположную сторону.
Формулу высоты выведем из формулы Герона
color{#0000FF}{p = Large{frac{a + b + c}{2}}}
color{#0000FF}{S = sqrt{p(p-a)(p-b)(p-c)}}
Где a, b, c – длины сторон треугольника, p – полупериметр
и формулы площади треугольника
color{#0000FF}{S = Largefrac{1}{2}normalsize*b*h_b}
Выведем высоту треугольника
color{#0000FF}{Largefrac{1}{2}normalsize*b*h_b = sqrt{p(p-a)(p-b)(p-c)}}
Формулы высот треугольника
color{#0000FF}{h_b = Largefrac{2sqrt{p(p-a)(p-b)(p-c)}}{b}}
color{#0000FF}{h_a = Largefrac{2sqrt{p(p-a)(p-b)(p-c)}}{a}}
color{#0000FF}{h_c = Largefrac{2sqrt{p(p-a)(p-b)(p-c)}}{c}}
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
-
Нахождение высоты треугольника
-
Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
- Высота в прямоугольном треугольнике
- Высота в равностороннем треугольнике
-
Высота в разностороннем треугольнике
- Примеры задач
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Здесь рассмотрены все возможные способы нахождения высоты треугольников разных типов. Высота
треугольника – отрезок, проведенный из вершины треугольника перпендикулярно к противоположной
стороне. В задачах нахождение высоты часто является промежуточным звеном для поиска других значений.
Она и является катетом в треугольнике, который сама же образует, и участвует во многих формулах,
например, для нахождения площади.
- Высота разностороннего треугольника через площадь и длину
стороны - Высота разностороннего треугольника через длины всех
сторон - Высота разностороннего треугольника через длину прилежащей
стороны и синус угла - Высота разностороннего треугольника через стороны и радиус
описанной окружности - Высота равнобедренного треугольника через основание и
боковые стороны - Высота прямоугольного треугольника через длины отрезков,
образованных на гипотенузе - Высота прямоугольного треугольника через все стороны
треугольника - Высота равностороннего треугольника через сторону
треугольника
Через площадь и длину стороны разностороннего треугольника
Через площадь и длину высота находится по формуле:
h = 2S / a
где S – площадь треугольника, а – сторона треугольника.
Цифр после
запятой:
Результат в:
Согласно этой формуле высота равна удвоенной площади, деленной на длину стороны, к которой она
проведена.
Пример. Найдите высоту разностороннего треугольника, проведенную к стороне а,
площадь которого равна 27 см, а длина стороны а составляет одну треть от площади. Решение: Найдем
сторону а. Так как известно, что она составляет треть от площади, а = 27 / 3 = 9 см.
Теперь воспользуемся формулой для нахождения высоты: h = 2S / a. Подставим
известные значения. h = 2 * 27 / 9 = 6 см. Ответ: 6 см
Через длины всех сторон разностороннего треугольника
Через длины всех сторон высота разностороннего треугольника ищется по формуле:
h = (2 √(p (p-a)(p-b)(p-c))) / 2
p = (a + b + c) / 2
где h – высота, а, b, c – стороны треугольника, p – полупериметр треугольника.
Цифр после
запятой:
Результат в:
Полупериметр треугольника можно найти либо в два этапа через периметр, либо сразу по формуле. Этим
способом удобно пользоваться, когда треугольник разносторонний.
Пример. Периметр разностороннего треугольника равен 18 см. Длины сторон 6 см и 8 см. Найдите
высоту, проведенную к стороне а. Решение: P = a + b + c, значит с = P – a – b , то есть c = 18 – 8 – 6 = 4 см. Для
нахождения h будем использовать формулу h = (2 √(p (p-a)(p-b)(p-c))) / 2.
Сначала найдем полупериметр (p): p = p / 2 = 18 / 2 = 9 см. Подставим,
найденные значения в формулу высоты: h = (2 √(9 (9 — 6)(9 — 8)(9 — 4))) / 2 = √135 / 3 = 2,12 см
Через длину прилежащей стороны и синус угла разностороннего треугольника
Через длину прилежащей стороны и синус угла высота ищется по следующей формуле:
h = a * sin α
где а – длина стороны, sin α – синус прилежащей стороны.
Цифр после
запятой:
Результат в:
Пример. В разностороннем треугольнике высота проведена к стороне AB. Угол ACH равен
30˚, а длина стороны AB 12 см. Найдите длину высоты CH в треугольнике ABC. По теореме о сумме углов
в треугольнике найдем угол САН. ∠САН = 180 – (∠АСН + ∠АНС). ∠САН = 180 – 90 – 30 = 60˚ sin 60º = 1/2. СН = AB * sin ∠САН, СН = 12 * 1/2 = 6 см. Ответ:
6 см
Через стороны и радиус описанной окружности разностороннего треугольника
Через стороны и радиус описанной окружности высоту можно найти по следующей формуле:
h = bc / 2R
где r – радиус описанной около треугольника окружности, b,c – стороны треугольника
Цифр после
запятой:
Результат в:
Пример. Вокруг разностороннего треугольника описана окружность с радиусом 3 см. Из
вершины между сторонами b и с проведена высота. Стороны b и с соответственно равны 5 см и 6 см.
Найдите высоту. Решение: Найдем высоту, используя формулу h = 5 * 6 / 2 * 3 = 30 / 6 = 5 см. Ответ:
5 см.
Через длины отрезков прямоугольного треугольника, образованных на гипотенузе
Через длины отрезков образованных на гипотенузе высоту можно найти по следующей формуле:
h = √(C1 * C2)
где: C1, C2 — отрезки, образованные проведением высоты к гипотенузе.
Цифр после
запятой:
Результат в:
Пример. В прямоугольном треугольнике катеты равны 4 см и 3 см. Угол BAH равен 30˚.
Найдите высоту. По теореме Пифагора найдём сторону BC, которая является гипотенузой в треугольнике
ABC. BC² = AB² = AC², BC² = 4² + 3² = 16+9 = 25 см², BC = √25 = 5 см. Угол
АНВ равен 90˚, так как АН является высотой, то есть, проведена перпендикулярно к стороне ВС.
Следовательно, треугольник АНВ – прямоугольный. Сторона ВН лежит напротив угла 30˚ в прямоугольном
треугольнике, значит, ее длина равна половине длины гипотенузы. Найдем ВН. BH = 1/2 AB. BH = 1/2 × 4 = 2 см. BC = BH + HC,
значит, HC = BC – BH, HC = 5 – 2 = 3 см. По формуле найдем высоту
(АН). АН = √(2 * 3) = √6 = 2,4 см. Ответ: 2,4 см.
Через основание и боковые стороны равнобедренного треугольника
Через основание и боковые стороны высота равнобедренного треугольника находится по формуле:
h = √(b² — a²/4)
где а – основание треугольника, b – боковая сторона. Для равнобедренного треугольника.
Цифр после
запятой:
Результат в:
Пример. В равнобедренном треугольнике АВС боковая сторона равна 8 см. Из вершины В к
основанию АС проведена высота ВН. Отрезок АН равен 5 см. Найдите высоту. Решение: Так как по условию
треугольник АВС равнобедренный по условию, то АВ = ВС = 8 см высота ВН,
является и медианой, и биссектрисой. Значит, АН = НС, а АС = НС + АН, АС = 5 + 5 = 10 см. По
формуле найдем высоту ВН = √(АВ² — АС² / 4). ВН = √(8² — 10² / 4) = √(64 — 100 / 4) = √39 = 6 см.
Ответ: 6 см.
Высота прямоугольного треугольника через все стороны треугольника
Если известны все стороны прямоугольного треугольника, то можно найти его высоту по следующей
формуле:
h = ab / c
где a,b,c – стороны треугольника.
Цифр после
запятой:
Результат в:
Пример. В прямоугольном треугольнике угол между катетом и гипотенузой равен 45˚.
Длина стороны АС равна 6 см. Найти высоту АН. Решение: По теореме о сумме углов в треугольнике
найдем угол АСВ. ∠АСВ = 180˚ – (45˚ + 90˚) = 45˚. Так как АСВ = АСВ, то
треугольник АВС равнобедренный с основанием ВС. Таким образом, АС = АВ = 6 см. По теореме Пифагора найдем гипотенузу ВС. BC² = AB² + AC². BC² = 6² + 6² = 36 +36 = 72 см². ВС = √72 = 6√2 см. Найдем
высоту по формуле AH = AB * AC / BC. АН = 6 * 6 / 6√2= см. Домножим
полученное значение на √2: (6 * √2) / √2 * √2 = 6√2 / 2 = 3√2 см. Ответ:
3√2 см
Через сторону равностороннего треугольника
Высота равностороннего треугольника через сторону треугольника ищется по следующей формуле:
h = a√3 / 2
где a – сторона треугольника.
Цифр после
запятой:
Результат в:
Пример: Найдите высоту в равностороннем треугольнике, если известно, что его сторона
равна 4√3 см. Решение: Для нахождения высоты воспользуемся формулой h = a√3 / 2 = √3 * 4 √3 / 2 = 4 * 3 / 2 = 6 см. Ответ:
6 см
В зависимости от типа треугольника высота может располагаться по-разному:
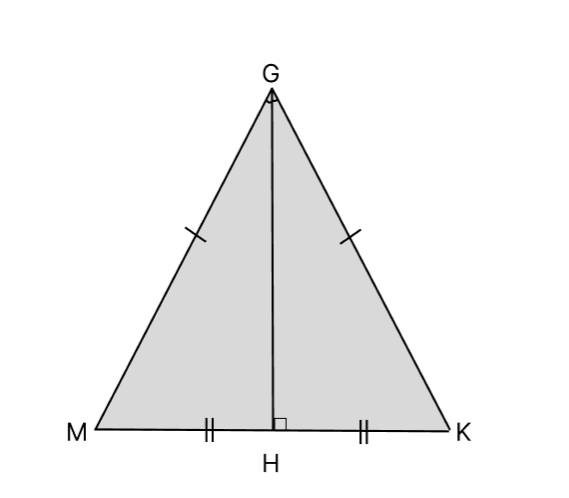
- Например, в треугольнике KGM высота GH, проведённая из вершины G к стороне находится внутри
треугольника, так как треугольник является остроугольным. Кроме того, треугольник в данном
примере равнобедренный, значит, она же является биссектрисой и медианой. Знание этого пригодится
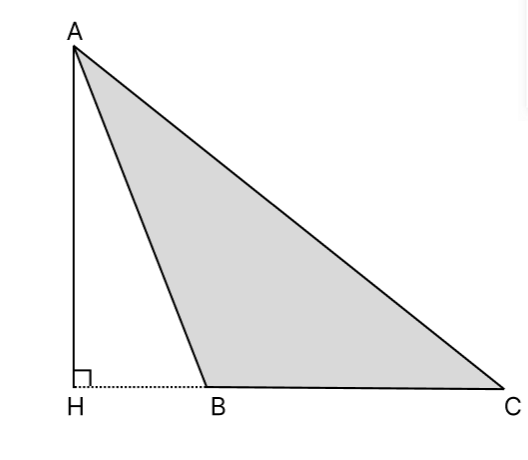
при решении задач, например таким образом можно будет найти основание. - В тупоугольном треугольнике высота будет выходить за его пределы и для того чтобы её провести
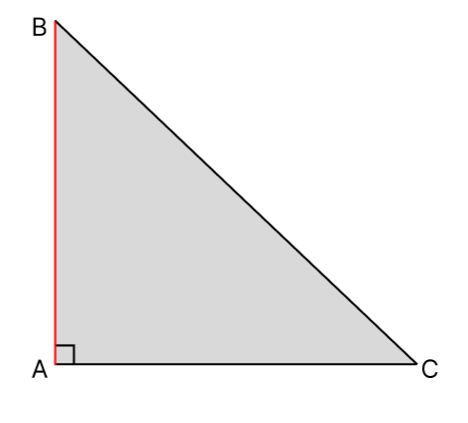
понадобится сначала продлить сторону. Например, на рисунке сторона ВС продлена до НС. - В случае, когда треугольник имеет прямой угол – высота совпадёт с одним из катетов, либо будет
внутри треугольника (как в первом рассмотренном варианте) и проведена к гипотенузе.
Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Высота треугольника
В произвольном треугольнике (у которого все стороны разной длины), высоты, проведенные к сторонам , медианы и биссектрисы представляют собой совершенно разные линии. Чтобы найти длину высоты в треугольнике, нельзя будет использовать свойства медианы или биссектрисы, как для равнобедренных или равносторонних треугольников, поэтому придется использовать другие методы.
Один из подобных методов заключается в использовании общего параметра треугольника – площади. Алгоритм вычислений строится на том, что площадь разностороннего треугольника можно найти несколькими способами, в том числе и через высоту. Зная три стороны треугольника, можно найти его площадь по формуле Герона, а затем используя другую формулу площади, выразить через нее высоту.
Чтобы вычислить площадь треугольника по формуле Герона, нужно сначала рассчитать полупериметр треугольника. Как следует из названия, полупериметр – это периметр, то есть сумма длин всех трех сторон, деленный на два.
Сама формула площади представляет собой произведение полупериметра на его разности с каждой стороной, все это выражение будучи заключенным под квадратным корнем.
С другой стороны та же площадь треугольника через высоту равна половине произведения стороны треугольника на высоту, на нее опущенную. Отсюда высота будет равна отношению удвоенной площади к стороне треугольника. Из предыдущей формулы можно выразить площадь через три стороны треугольника и заменить ее в формуле высоты.
Данная формула высоты через стороны треугольника применима для любых треугольников, произвольных, равнобедренных или равносторонних за отсутствием других.
Вычисляя высоту треугольника, зная три стороны, приходится идти длинным путем, используя формулы площади. Высота треугольника, выраженная через площадь, связана только с той стороной, на которую она опущена, поэтому чрезвычайно важно правильно указать для калькулятора порядок сторон и в ручном расчете подставить соответствующую сторону в формулу высоты.
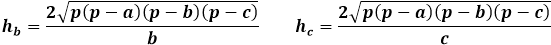
Формула высоты произвольного треугольника через площадь
Все формулы высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
[spoiler title=”источники:”]
http://allcalc.ru/node/992
http://www-formula.ru/heighttriangle
[/spoiler]
Условие задачи: как найти высоту в треугольнике
если известны все 3 стороны!
Иногда, задача имеет несколько решений.
Но в чем прелесть математики, то это – её простота для меня и сложность для того, кто не знает её!
Это – очередная задача от моих племянников, за которыми мне приходится все решать….
На самом деле – эта задача очень простая!
Нам понадобится 2 формулы.
- Формула Герона – нахождение площади треугольника по трём сторонам.
- Формула – определения площади через высоту.
Выразив высоту через площадь, и заменив площадь на формулу Герона получим высоту через периметр, т.е. через три стороны…
Мы уже разбирали, как найти площадь треугольника если известны все стороны, напоминаю формулу Герона:
где p равно
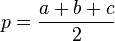
И, так же, мы разбирали, как найти площадь, если известна высота и одна из сторон, напоминаю формулу:
S = b х h / 2
Отсюда нам лишь нужно вывести чему равна высота треугольника:
Умножаем на 2:
2 S = b х h
Делим на сторону:
Перевернем для удобства и получим, что высота треугольника равна площади умноженную на 2 и деленную на сторону.
h = 2 S / b
Ну, и далее, площадь “S” нужно заменить на верхнюю формулу .
Вот и всё!
Написать что-нибудь…
найти , высоту треугольника , если известны 3 стороны , как найти высоту треугольника по 3 сторонам