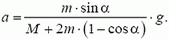Высота правого клина Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Длина края правого клина: 10 метр –> 10 метр Конверсия не требуется
Базовая ширина правого клина: 5 метр –> 5 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
9.68245836551854 метр –> Конверсия не требуется
4 Высота правого клина Калькуляторы
Высота правого клина формула
Высота правого клина = sqrt(((4*Длина края правого клина^2)-Базовая ширина правого клина^2)/4)
h = sqrt(((4*le^2)-wBase^2)/4)
Что такое правый клин?
Прямой клин — это клин с параллельными боковыми треугольниками. Он имеет прямоугольное основание, две прямоугольные грани и два равнобедренных треугольника.
Что такое клин?
В твердотельной геометрии клин представляет собой многогранник, состоящий из двух треугольников и трех граней трапеции. У него пять граней, девять ребер и шесть вершин. Это подкласс призматоидов с основанием и противоположным ребром в двух параллельных плоскостях. Его также можно отнести к диагональному куполу.
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
|||
|
Здравствуйте! Помогите, пожалуйста, с решением! Задача: тело массой m, двигаясь по горизонтальной плоскости со скоростью V, заезжает на гладкий клин массой M. Найдите, на какую высоту поднимется тело по клину. Трением пренебречь! Тело заезжает на клин плавно, без удара! Спасибо!
|
||
| Вернуться к началу |
|
||
|
vera |
Заголовок сообщения: Re: Закон сохранения энергии
|
|
не могли бы вы расписать необходимые формулы?
|
|
| Вернуться к началу |
|
|
vera |
|
||
|
mV=(m+M)U отсюда U=mV/(m+M) найдем кинетическую энергию клина. на вершине клина кинетическая энергия тела=0. а вот потом что делать не совсем понятно…
|
|||
| Вернуться к началу |
|
||
|
vera |
|
||
|
до взаимодействия у нас потенциальная энергия тела была равна нулю. мне представляется это так: mv^2/2=(M*(mV/(m+M))^2)/2 +mgh
|
|||
| Вернуться к началу |
|
||
|
vera |
|
||
|
Так, понятно, а до взаимодействия энергия системы будет равна кинетической энергии тела?
|
|||
| Вернуться к началу |
|
||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найдите, на какую максимальную высоту H поднимется груз
в форуме Школьная физика |
goldolov_na |
40 |
787 |
25 янв 2020, 04:08 |
|
На какую высоту поднимется груз привешеный к поршню
в форуме Молекулярная физика и Термодинамика |
Kikki |
1 |
1093 |
06 июн 2013, 16:27 |
|
На какую высоту можно поднять тело
в форуме Молекулярная физика и Термодинамика |
oksanakurb |
1 |
809 |
07 окт 2013, 08:36 |
|
Найти высоту
в форуме Геометрия |
ilyall3 |
1 |
172 |
23 окт 2019, 20:14 |
|
Найти высоту
в форуме Геометрия |
kicultanya |
13 |
1038 |
04 мар 2018, 19:46 |
|
Найти высоту СН
в форуме Геометрия |
kicultanya |
9 |
354 |
02 янв 2017, 12:18 |
|
Найти высоту параллелепипеда
в форуме Аналитическая геометрия и Векторная алгебра |
sfanter |
3 |
580 |
08 ноя 2015, 05:45 |
|
Найти высоту пирамиды
в форуме Геометрия |
lika01 |
5 |
1382 |
10 май 2014, 13:30 |
|
Найти высоту трапеции
в форуме Геометрия |
irusha |
10 |
1233 |
10 сен 2013, 11:37 |
|
Найти высоту параллелепипеда
в форуме Аналитическая геометрия и Векторная алгебра |
HUEHUEHUE |
1 |
3129 |
12 окт 2014, 19:54 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: Google [Bot] и гости: 1 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
В пазах
роторов и якорей располагаются обмотки,
на которые при вращении действуют
центробежные силы. Для предотвращения
перемещения в радиальном направлении
обмотки должны быть надежно закреплены.
Лобовые
части обмоток закрепляют бандажами,
намотанными из проволоки или стекловолокна.
Закрепление пазовой части обмотки
посредством бандажей можно применять
для машин постоянного тока относительно
небольшой мощности (при диаметрах якоря
до 300…350 мм), имеющих открытые пазы.
Бандажи располагают в специальных
канавках магнитопровода, которые
образуются в результате применения
листов меньшего диаметра, чем основные
(рис. 8.50).

Рис. 8.50. Якорь машины постоянного
тока с креплением обмотки бандажами
Применение
бандажей имеет определенные преимущества,
так как при этом уменьшается высота
зубца, что приводит к уменьшению
магнитного напряжения зубцов и потерь
при их перемагничивании. Однако при
больших скоростях (при
![]()
>
35 м/с) применение бандажей становится
нерациональным, так как бандажи
перекрывают чрезмерно большую поверхность
якоря, что ухудшает его отдачу. При
наличии проволочных бандажей из-за
потерь в них понижается КПД машины, а
при бандажах из магнитной проволоки
ухудшается коммутация. При наличии
кольцевых канавок увеличивается
воздушный зазор, а, следовательно, и
магнитное напряжение зазора. Поэтому
у более мощных машин постоянного тока,
имеющих на роторе (якоре) полузакрытые
пазы, крепление обмоток в активной части
производят клиньями.
Расчет
бандажей. Для
бандажей применяют магнитную или
стальную немагнитную проволоку или
стеклоленту. При частотах перемагничивания
более 50 Гц и в напряженных по коммутации
машинах на активной части преимущественно
применяют немагнитную проволоку. Диаметр
проволоки для бандажей предварительно
выбирают в пределах 0,8…2,0 мм (меньшие
диаметры проволоки берут для машины с
меньшим диаметром якоря).
Для
уменьшения потерь бандаж делят на части,
для чего по длине магнитопровода делают
несколько канавок. Длину каждой канавки
следует принимать не более 15.. .20 мм, а
общая длина всех канавок не должна
превышать 35% длины магнитопровода. На
лобовых частях обмотки ширина бандажей
может достигать 40 мм. Более широкие
бандажи также следует делить на части
или применять укладку в несколько слоев
по высоте.
Под
проволочными бандажами на пазовой и
лобовой частях обмотки якоря подкладывают
миканит толщиной 0,3. ..0,4 мм. Внешний
диаметр установленных бандажей не
должен превышать внешнего диаметра
якоря. Для укрепления бандажей по ширине
применяют скрепки из белой жести шириной
8. ..15 мм, припаиваемые оловянным припоем
(рис. 8.51).

Рис. 8.51. Крепление концов проволоки
бандажей якоря:
а — на
магнитопроводе; б
— на лобовых частях обмотки
По
сравнению с проволочными бандажи из
стеклоленты, пропитанной синтетическими
смолами, имеют преимущества. У них нет
собственных потерь, они не требуют
наложения изоляции между бандажом и
обмоткой, менее трудоемки в изготовлении.
Недостатком таких бандажей является
их большая толщина, так как стеклолента
имеет меньшую механическую прочность.
При
расчете бандажа исходят из того, что он
испытывает напряжение от центробежных
сил обмотки и самого бандажа. Число
витков проволочного бандажа
![]() ,
,
(8.103)
где
![]() — диаметр проволоки бандажа, м;
— диаметр проволоки бандажа, м;![]() — допустимое напряжение растяжения,
— допустимое напряжение растяжения,
принимаемое для стальной бандажной
проволоки равным 450·106
Па;
![]()
—
максимальная частота вращения, об/мин;
![]() — напряжение от центробежных сил
— напряжение от центробежных сил
бандажа, Па.
Для бандажей из
стали
![]() ,
,
(8.104)
При
определении числа витков бандажа,
располагаемого на магнитопроводе, в
(8.103) подставляют массу проводников
![]() и изоляции
и изоляции![]()
пазовой
части
обмотки,
кг:
![]() ,
,
(8.105)
где
![]()
—
число пазов якоря;
![]() —
—
полная длина магнитопровода якоря, м;![]() — по (8.101).
— по (8.101).
Для
нахождения винтов бандажа с одной
стороны лобовой части в (8.103) подставляют
массу
![]() ,
,
кг:
![]() ,
,
(8.106)
где
![]() — длина лобовой части проводника, м;
— длина лобовой части проводника, м;![]()
—
площадь поперечного сечения проводника,
м2;
коэффициент 1,2 приближенно учитывает
массу изоляции.
Число витков
бандажа из стеклоленты определяют по
формула
![]() ,
,
(8.107)
где
![]() —
—
площадь
поперечного сечения ленты, м2;
![]() — допустимое напряжение растяжения,
— допустимое напряжение растяжения,
равное 150·106
Па для стеклоленты класса нагревостойкости
![]() и 130·106
и 130·106
Па
для
класса![]() .
.
Для бандажей из
стеклоленты, Па,
![]() .
.
(8.108)
Для
бандажей используется лента ЛСБ (ТУ
6.11.22) толщиной 0,18. ..0,2 мм и шириной 10, 15,
20, 25, 30 мм. Высоту бандажных канавок на
магнитопроводе якоря выбирают равной
от 2 до 3,5 мм.
Пример. Двигатель
постоянного тока имеет данные:
![]() кВт, максимальная эксплуатационная
кВт, максимальная эксплуатационная
частота вращения (при ослаблении поля)
2200 об/мин,![]() м,
м,![]() м,
м,![]() ,
,![]() м,
м,![]() м;
м;![]() м2,
м2,
![]() м2.
м2.
Из (8.101)
![]() кг.
кг.
Масса пазовой части обмотки с изоляцией
по (8.105)
![]() кг.
кг.
Напряжение от центробежных сил по
(8.108)
![]() Па.
Па.
По (8.107)
![]() .
.
Расчет
клиньев. Клинья
изготовляют из гетинакса, текстолита,
стеклотекстолита и дерева (бука, клена,
ясеня). Клин рассчитывают на изгиб как
балку с сосредоточенной нагрузкой
посредине. Эта нагрузка
равна
центробежной силе пазовой части обмотки.
Расчет производится на 1 м. Исходя из
этого определяется предварительная
высота клина
![]() ,
,
(рис. 8.51), м:
![]() .
.
(8.109)
Центробежная сила
пазовой части обмотки на 1 м, Н/м,
![]() ,
,
где
![]() — по (8.101);
— по (8.101);![]()
— средняя
ширина клина, м (рис. 8.52),
![]() .
.
Допустимое
напряжение на изгиб
![]() для гетинакса равно 20 МПа, для текстолита
для гетинакса равно 20 МПа, для текстолита
— 35 МПа, для дерева при расположении
волокон поперек паза — 8 и вдоль паза —
4 МПа.
По
найденной высоте
![]() из табл. 8.9 подбирают нормализованные
из табл. 8.9 подбирают нормализованные
размеры клина. Приведенные в таблице
размеры даны в соответствии с рис. 8.52.
По производственным соображениям высота
клина должна составлять не менее 0,256![]() .
.
После
выбора клина проводят поверочный расчет.
Напряжение на изгиб, Па,
![]() .
.
(8.110)
Напряжение
на срез, Па,
![]() ,
,
(8.111)
где
![]()
—
в метрах по рис. 8.52 и табл. 8.9.
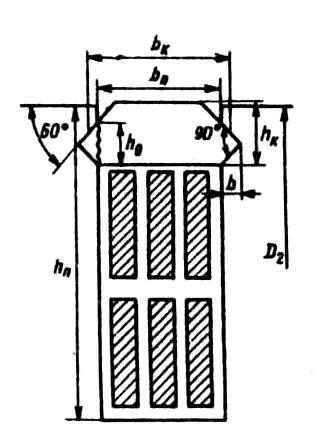
Рис. 8.52. К расчету пазового клина
Таблица 8.9. Размеры клина
|
|
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
2,5 |
3,5 |
4,5 |
5,5 |
6,5 |
7 |
Допустимое
напряжение на срез для гетинакса равно
10 МПа, для текстолита — 15 МПа, для дерева
при расположении волокон поперек паза
— 4 и вдоль паза — 2 МПа.
Пример. Тот же двигатель, что и в
предыдущем примере (![]() кВт). Размеры паза
кВт). Размеры паза![]() м. Остальные данные те же.
м. Остальные данные те же.
Из (8.101)
![]() кг.
кг.
Центробежная сила пазовой части обмотки
![]() Н/м.
Н/м.
Материал клина — текстолит с
![]() МПа. Выбираем
МПа. Выбираем![]() =14·10-3м.
=14·10-3м.
Из (8.109)
![]() м.
м.
По табл. 8.9 выбираем клин с
![]() =
=
4·10-3м;![]() = 12 + 1,2 = 13,2 мм;
= 12 + 1,2 = 13,2 мм;![]() = 3,5 мм.
= 3,5 мм.
Проводим проверку:
По (8.110)
![]() Па;
Па;
по (8.111)
![]() Па.
Па.
Выбранный клин имеет достаточную
механическую прочность.
Соседние файлы в папке Копылов учебник (doc)
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Высота – клин
Cтраница 1
Высота клина принимается равной / гк 2 5 мм, высота шлица Лш1 0 мм.
[1]
Высота клина принимается равной Ак 2 5 мм, высота шлица Аш 1 0 мм.
[3]
Высота клина Л, соответствующая сомкнутому положению ползунов, должна приниматься на 2 – 3 мм больше высоты отверстия, оформляемого указанным выше знаком.
[4]
Высота клина принимается равной йк 2 5 мм, высота шлица йш 1 0 мм.
[6]
Высота клина Л2 может быть определена из условий работы его на изгиб и на срез. Размеры клина, полученные при расчете на срез, не гарантируют его от изгиба; напротив, размеры клина, найденные из расчета на изгиб, исключают возможность среза.
[7]
Высота клина зависит от глубины промерзания. Угол заострения клина а при сколе грунта назначается в пределах 20 – 30; при этом лучше работает односкосный клин.
[9]
Высоту клина hcp определяют из расчета на изгиб. Средний участок клина, равный do, нагружен равномерно распределенной нагрузкой. Опасное сечение находится в середине пролета.
[10]
Высоту клина hcp определяют из расчета на изгиб. Средний участок клина, равный d0, нагружен равномерно распределенной нагрузкой. Опасное сечение находится в середине пролета.
[11]
Высоту клина определяем из расчета на изгиб [ а ] изг M / W M / ( dh2 / 6) [ а ] изг, где М l 25FD / 8 – изгибающий момент в опасном сечении клина; W – осевой момент сопротивления; [ о ] изг 100 150 МПа – допускаемое напряжение изгиба.
[13]
Определяют высоту клина из условия прочности на изгиб.
[14]
Если при уменьшении высоты клина натяг хвостовика валика недостаточен при капитальном ремонте тепловозов, его восстанавливают до чертежных размеров путем наплавки и последующей обработки клиновых пазов на раме тележки и буксах.
[15]
Страницы:
1
2
3
4
5
Черноуцан А.И. Кинематические связи в задачах динамики // Квант. — 1988. — № 2. — С. 57-62.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В задачах по механике часто встречается ситуация, когда движение тел не является свободным. Ограничения могут создавать твердые поверхности, нерастяжимые нити, жесткие стержни и т. п.
В простейших случаях мы учитываем подобные ограничения автоматически, часто даже не оговаривая их существования. Например, ускорение тела на плоскости мы направляем вдоль плоскости (учитывая наличие твердой поверхности), скорости буксира и баржи считаем одинаковыми (принимая во внимание присутствие нерастяжимого троса) и т. д. Однако иногда возникает необходимость выразить эти ограничения в виде специального уравнения, которое мы будем называть «кинематической связью». Начнем с такой задачи.
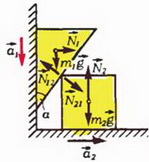
Задача 1. Найдите ускорения призмы массой m1 и куба массой m2, изображенных на рисунке 1, а. Трением пренебречь.
а
б
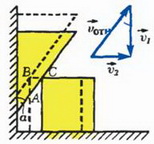
Рис. 1.
Запишем второй закон Ньютона для каждого тела (в проекции на направление, совпадающее с соответствующим ускорением):
m1·g – N·sin α = m1·a1, (1)
N·cos α = m2·a2. (2)
Мы учли, что по третьему закону Ньютона 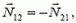 т. е. N12 = N21 = N. Написанные два уравнения содержат три неизвестных. Третье уравнение — кинематическая связь между а1 и a2 — должно отразить тот факт, что куб и призма остаются все время в контакте друг с другом. Это можно сделать несколькими способами.
т. е. N12 = N21 = N. Написанные два уравнения содержат три неизвестных. Третье уравнение — кинематическая связь между а1 и a2 — должно отразить тот факт, что куб и призма остаются все время в контакте друг с другом. Это можно сделать несколькими способами.
1) Рассмотрим два близких положения системы, разделенные промежутком времени Δt (рис. 1, б). В треугольнике ABC сторона АВ равна перемещению призмы Δx1, а сторона ВС — перемещению куба Δx2. Имеем
Δx2 = Δx1·tg α.
Разделив обе части равенства на Δt, получаем
υ2 = υ1·tg α.
Так как это соотношение справедливо для произвольного момента времени, из него следует искомое соотношение
a2 = a1·tg α. (3)
Такой подход к получению кинематической связи будем называть прямым методом.
2) Другой способ получения необходимой связи основан на переходе в такую систему отсчета, где условие контакта становится тривиальным. В системе отсчета, связанной с призмой (см. рис. 1, б), скорость куба 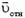 направлена вдоль ее поверхности, т. е. под углом α к вертикали. Записывая закон сложения скоростей
направлена вдоль ее поверхности, т. е. под углом α к вертикали. Записывая закон сложения скоростей
![]()
из соответствующего векторного треугольника получаем
υ2 = υ1·tg α и a2 = a1·tg α.
Решаем совместно уравнения (1)-(3) и находим
![]()
В этой задаче второй метод выглядит несколько искусственно. Однако в некоторых случаях именно правильный выбор системы отсчета позволяет существенно упростить проблему кинематических связей. Вот пример.
Задача 2. Клин высотой h с углом наклона α стоит на гладкой горизонтальной плоскости (рис. 2). Масса клина m1. С вершины клина начинает соскальзывать без трения брусок массой m2. Найдите ускорение клина и время соскальзывания бруска.
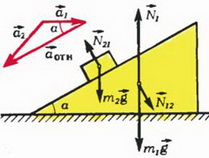
Рис. 2.
Начнем со второго закона Ньютона. Запишем его для клина в проекции на горизонтальное направление, а для бруска пока что в векторной форме:
N·sin α = m1·a1, (4)
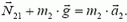 (5)
(5)
Как и раньше, 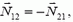 т. е. N12 = N21 = N. Выбор направления осей для бруска связан с решением вопроса о кинематической связи.
т. е. N12 = N21 = N. Выбор направления осей для бруска связан с решением вопроса о кинематической связи.
Кинематическая связь между ускорениями должна отразить тот факт, что в процессе движения брусок все время остается на поверхности клина. Записать это в виде прямого уравнения оказывается непросто. Вместо этого перейдем в систему отсчета, связанную с клином. В этой системе скорость бруска 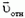 и его ускорение
и его ускорение 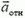 направлены вдоль клина. Тогда из закона сложения скоростей
направлены вдоль клина. Тогда из закона сложения скоростей 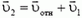 получаем закон сложения ускорений (см. рис. 2)
получаем закон сложения ускорений (см. рис. 2)
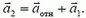 (6)
(6)
Отсюда видно, что от неизвестных a1 и a2 удобнее перейти к неизвестным a1 и aотн, решив тем самым проблему кинематической связи. Подставляя равенство (6) в уравнение (5) и проектируя это уравнение на направления вдоль поверхности клина и перпендикулярно к ней, получаем
m2·g·sin α = m2·(aотн – a1·cos α), (5׳)
N – m2·g·cos α = –m2·a1·sin α. (5״)
Из уравнений (4), (5′) и (5″) находим
![]()
Для ответа на второй вопрос задачи нам не надо искать a1, так как время соскальзывания выражается как раз через aотн:
![]()
Отсюда находим
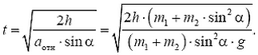
Как уже говорилось, ограничение на движение может определяться не только прямым контактом рассматриваемых тел, но и наличием в системе соединительных элементов — стержней, нитей и т. п. В большинстве случаев, даже если в условии это не оговорено, соединительные элементы считаются идеальными, т. е. нити — невесомыми и нерастяжимыми, стержни — невесомыми и абсолютно жесткими, для блоков кроме невесомости предполагается также отсутствие трения на оси. (На самом деле слово «невесомый» означает, что масса данного элемента пренебрежимо мала по сравнению с массами других тел системы, слово «нерастяжимый» — что удлинение элемента мало по сравнению с перемещениями тел системы и т. д.) Перед тем, как разбирать конкретные примеры, выясним, что следует из идеальности соединительных элементов. Рассмотрим три частных случая.
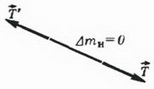
1. Невесомость нити. Напишем второй закон Ньютона для участка нити массой Δmн (рис. 3, а):
T – T´ = Δmн·a.
Так как Δmн = 0, то T – T´, т. е. сила натяжения не меняется вдоль нити.
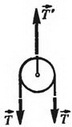
2. Невесомость подвижного блока и отсутствие трения на его оси. Для раскручивания невесомого блока, в котором нет трения, не нужен вращательный момент. Из этого следует, что натяжение одной и той же нити по обе стороны блока одинаково (рис. 3, б), кроме того
T´ – 2T = 0, т. е. T´ = 2T.
3. Невесомость стержня. Это условие означает, что сумма сил и сумма моментов сил, действующих на стержень, равны нулю. Например, если к стержню приложены две силы, то они равны по модулю, противоположны по направлению и действуют вдоль стержня (рис. 3, в). (В отличие от нити, стержень может быть не только в растянутом, но и в сжатом состоянии.)
а
б
![]()
в
Рис. 3.
Нерастяжимость и жесткость нитей и стержней приводит к появлению кинематических связей, которые мы разберем отдельно в следующих задачах.
Задача 3. Найдите ускорения грузов массой m1 и m2 после перерезания верхней нити (рис. 4). Нити и блок считать идеальными.
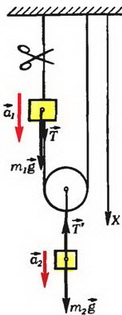
Рис. 4.
Выберем положительное направление оси вертикально вниз и запишем второй закон Ньютона для обоих тел:
T + m1·g = m1·a1, (7)
m2·g – 2T = m2·a2 (8)
(мы учли свойства блока и нити, описанные выше).
Для нахождения кинематической связи между a1 и а2 применим, как мы его назвали, прямой метод. Запишем длину нити в виде
l = x2 + π·R + (x2 – x1),
где х1 — координата груза массой m1, x2 — координата центра блока, R — его радиус, и учтем, что длина нити при движении грузов не изменяется. Тогда для перемещений грузов получим соотношение
2Δx2 – Δx1 = 0,
откуда
2υ2 – υ1 = 0,
2a2 – a1 = 0. (9)
Решая уравнения (7)-(9) совместно, находим
![]()
(Обратите внимание на то, что a1 > g. Подумайте, почему получился такой ответ.)
Задача 4. Невесомый стержень с одинаковыми грузами массой m на концах шарнирно закреплен на оси, которая делит его длину в отношении 2:1 (рис. 5). Стержень удерживают в горизонтальном положении и в некоторый момент освобождают. Найдите ускорения грузов сразу после этого, а также давление стержня на ось в этот момент.
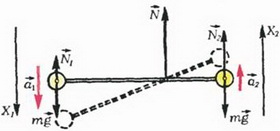
Рис. 5.
Запишем второй закон Ньютона для грузов, выбрав положительные направления осей в сторону соответствующих ускорений:
m·g – N1 = m·a1, (10)
N2 – m·g = m·a2, (11)
где N1 и N2 — силы, действующие на грузы со стороны стержня. Так как сумма моментов сил, действующих на невесомый стержень, равна нулю, то
![]()
где l — длина стержня. Отсюда
N2 = 2N1. (12)
Осталось записать кинематическую связь между a1 и а2. Для этого изобразим на рисунке 5 положение стержня через малый промежуток времени Δt после начала движения. Из подобия получаем
x1 = 2x2,
откуда
υ1 = 2υ2,
a1 = 2a2. (13)
Решая совместно уравнения (10)-(13), находим
![]()
Так как сумма сил, действующих на невесомый стержень, равна нулю, то сила реакции оси (равная по модулю силе давления на ось) равна
![]()
***
Во многих задачах, рассчитанных на применение закона сохранения энергии, требуется найти скорости тел к определенному моменту времени. В этом случае надо установить кинематические связи не между ускорениями, а между скоростями тел. При решении таких задач полезно использовать тот факт, что полная работа, совершаемая любым идеальным соединительным элементом, равна нулю. Физическая причина этого состоит в том, что в таком элементе не может запасаться никакая энергия — ни кинетическая (его масса равна нулю), ни потенциальная (элемент не деформируется).
Последнее утверждение требует пояснения. Может показаться, что даже при малой деформации очень жесткого стержня (или другого элемента) потенциальная анергия его деформации 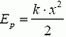 может быть велика — ведь она пропорциональна жесткости стержня k. Но если учесть, что сила F = k·x, возникающая при деформации, остается конечной при
может быть велика — ведь она пропорциональна жесткости стержня k. Но если учесть, что сила F = k·x, возникающая при деформации, остается конечной при 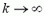 (она определяется движением тел, закрепленных на стержне), то потенциальная энергия
(она определяется движением тел, закрепленных на стержне), то потенциальная энергия 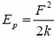 при больших k оказывается очень малой.
при больших k оказывается очень малой.
Эта и следующая задачи по своему уровню несколько выходят за пределы задач, предлагаемых обычно на вступительных экзаменах в вузы. Однако знакомство с ними для абитуриентов окажется небесполезным.
Задача 5. Груз массой М сначала удерживают на уровне блоков, а затем освобождают (рис. 6). Считая нити и блоки идеальными, размеры блоков малыми по сравнению с расстоянием 2l между ними, а массу m грузиков, висящих на концах нитей, известной, найдите скорость груза в тот момент, когда нити составляют угол α с вертикалью. Полученный ответ исследуйте.
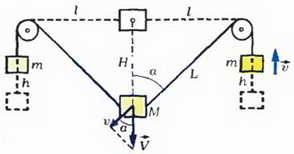
Рис. 6.
К рассматриваемому моменту груз массой М опустился на H = l·ctg α, а грузики массой m поднялись на 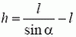 каждый. Согласно закону сохранения энергии,
каждый. Согласно закону сохранения энергии,
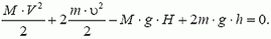 (14)
(14)
Для того чтобы найти связь между υ и V, можно, например, применить прямой метод. Из рисунка 6
l2 + H2 = L2.
Дифференцируя по времени (и учитывая, что l´ = 0), находим
2H·H´ = 2L·L´.
Так как L´ = υ, H´ = V, a H/L = cos α, то получаем искомую связь
υ = V·cos α. (15)
Однако проще получить это соотношение из следующих соображений. Раз расстояние L от груза массой М до блока в рассматриваемый момент увеличивается со скоростью υ (с такой скоростью вытягивается нить), то проекция скорости 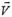 этого груза на направление нити должна быть равна υ. Учитывая, что скорость
этого груза на направление нити должна быть равна υ. Учитывая, что скорость 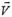 направлена вертикально, получаем уравнение (15).
направлена вертикально, получаем уравнение (15).
Из уравнений (14) и (15) находим
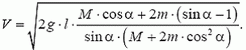
Выясним, будет ли центральный груз все время опускаться (мы считаем нити очень длинными) или при каком-то α он остановится и начнет подниматься. Уравнение V = 0 (условие остановки) преобразуется к виду
![]()
т. е. остановка и обратное движение грузов происходят только при М < 2m. Если М > 2m, то центральный груз будет все время перевешивать и его скорость будет неограниченно возрастать (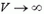 при
при 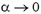 — проверьте это сами). Если же М = 2m, то при опускании центрального груза система все ближе подходит к равновесию, ускорения грузов стремятся к нулю, а их скорости — к предельному значению
— проверьте это сами). Если же М = 2m, то при опускании центрального груза система все ближе подходит к равновесию, ускорения грузов стремятся к нулю, а их скорости — к предельному значению 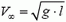 (убедитесь в этом самостоятельно).
(убедитесь в этом самостоятельно).
Хотелось бы обратить внимание на то, что при использовании закона сохранения энергии сила натяжения нити вообще не вошла в расчеты.
Последний пример иллюстрирует методы получения кинематических связей при движении твердых стержней (или других твердых связей). Напомним, что при движении твердого тела расстояние между любыми двумя его точками не изменяется.
Задача 6. Невесомый стержень длиной l с грузами массой m на концах соскальзывает по сторонам прямого двугранного угла (рис. 7, а). Найдите скорости грузов в тот момент, когда стержень составляет с горизонтом угол α. Трения нет. В начальный момент стержень находился в вертикальном положении.
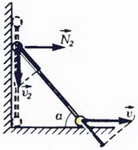
а
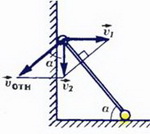
б
Рис. 7.
Из закона сохранения энергии получаем
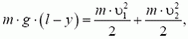 (16)
(16)
где y = l·sin α — координата второго груза в рассматриваемый момент. Для получения кинематической связи можно применить прямой метод, как это было сделано в предыдущей задаче (проделайте это сами). Быстрее же и нагляднее кинематическая связь получается из таких соображений. Раз расстояние между грузами остается неизменным, то в каждый момент скорость, с которой первый груз «удаляется» от второго, равна скорости, с которой второй груз «приближается» к первому. Иначе говоря, проекции скоростей грузов на стержень в любой момент времени одинаковы (см. рис. 7, a):
υ1·cos α = υ2·sin α. (17)
Подставляя (17) в (16), находим
![]()
В кинематике твердого тела часто используется «разложение» сложного движения на поступательное и вращательное. Чтобы продемонстрировать этот метод, применим его для получения кинематической связи (17). В системе отсчета, связанной с первым грузом, стержень совершает чисто вращательное движение. Значит, в этой системе скорость второго груза 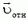 направлена перпендикулярно стержню. Применяя закон сложения скоростей
направлена перпендикулярно стержню. Применяя закон сложения скоростей 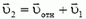 (см. рис. 7, б), получаем соотношение (17).
(см. рис. 7, б), получаем соотношение (17).
Может показаться, что найденные выражения для скоростей дают полное решение задачи. Однако в этой задаче содержится поучительный подвох, разбором которого мы и закончим статью.
Решение было бы полным, если бы второй груз не мог оторваться от вертикальной стены. (Для этого можно было бы, например, посадить грузы на гладкие штанги, а стержень присоединить к ним шарнирно). Однако в нашем варианте задачи (см. рис. 7, а) при некотором угле произойдет отрыв второго груза от вертикальной стены, после чего найденный ответ будет неприменим. Дело в том, что горизонтальный импульс системы определяется только движением первого груза, скорость которого, в соответствии с выражением для υ1, до некоторого угла возрастает, а потом начинает убывать. Это означает, что в какой-то момент должна изменить направление внешняя горизонтальная сила, действующая на систему. Но есть только одна горизонтальная сила — сила реакции вертикальной стенки, которая не может изменить свое направление. Таким образом, в тот момент, когда реакция стенки обращается в нуль, происходит отрыв второго груза от стенки. Дифференцируя выражение для υ1 по времени, находим, что υ1 максимальна при sin α = 2/3. При угле 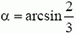 и происходит отрыв стержня от вертикальной стенки.
и происходит отрыв стержня от вертикальной стенки.
Упражнения
1. Найдите ускорения стержня и клина, изображенных на рисунке 8. Трения нет.
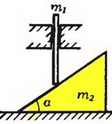
Рис. 8.
2. Найдите натяжение нити в системе, изображенной на рисунке 9.
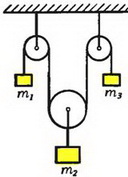
Рис. 9.
3. (для любителей каверз и ловушек). Чему равны ускорения грузов в системе, изображенной на рисунке 10?
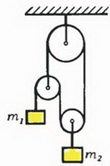
Рис. 10.
4. Найдите ускорение клина на рисунке 11. Трения нет. Указание. Примените метод, использованный при решении задачи 2 в статье.
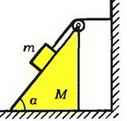
Рис. 11.
Ответы
1. 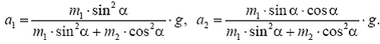
2. 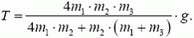
3. a1 = a2 = g.
4.