Как найти высоту когда даны только вектора

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Задача 22499 4. Зная две стороны vector = (-3;.

Условие

4. Зная две стороны vector = (-3; -2; 6), vector <ВС>= (-2; 4; 4) треугольника АВС, вычислить длину высоты AD.

Решение

Находим скалярное произведение векторов vector и vector.
vector=(3;2;-6)
vector *vector=(3)*(-2)+(2)*4-6*4=
=-22
Находим длины .векторов vector и vector.
|vector|^2=3^2+2^2+(-6)^2=49
|vector|=7
|vector|^2=(-2)^2+4^2+4^2=36
|vector|=6

cos(vector,vector)=-22/(7*6)=-11/21
sin(vector,vector)=sqrt(1-(-11/21)^2)=
=sqrt(1-(121/441))=8sqrt(5)/21

Как найти высоту пирамиды по векторам

Инструкция . Для решения подобных задач в онлайн режиме заполните координаты вершин, нажмите Далее . см. также по координатам треугольника найти.

• Решение онлайн
• Видеоинструкция
• Оформление Word

Пример №1 . В пирамиде SABC : треугольник ABC – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S . Сделать чертеж.
Решение: Координаты векторов находим по формуле: X = x₂ – x₁; Y = y₂ – y₁; Z = z₂ – z₁
Так, для вектора AB, это будут координаты: X = 0-2; Y = 3-0; Z = 0-0, или AB(-2;3;0).
AC(-2;0;1); AD(-2;2;3); BC(0;-3;1); BD(0;-1;3); CD(0;2;2) .
Длину вектора находим по формуле:

Пример №2 . В тетраэдре ABCD вычислить:

1. объем тетраэдра ABCD;
2. высоту тетраэдра, опущенную из вершины D на грань ABC.

A(2, 3, -2), B(3, 1, 0), C(-2, 2, 1), D(6, 1, -1)

Ответ

Проверено экспертом

Даны вершины пирамиды A(3;-2;3)B(-1;0;2)C(-3;1;-1)D(-3;-3;1) .

Находим векторы АВ, АС и АД.

Вектор АВ = (-4; 2; -1 ), модуль равен √(16+4+1) = √21 ≈ 4,58258.

Определяем векторное произведение АВ х АС.

-6 3 -4 | -6 3 = -8i + 6j – 12k – 16j + 3i + 12k = -5i – 10j = (-5; -10; 0).

Далее находим смешанное произведение (АВ х АС) х АД.

(АВ х АС) = (-5; -10; 0),

(АВ х АС) х АД = 30 + 10 + 0 = 40.

Объем пирамиды равен (1/6) этого произведения:

V = (1/6)*40 = (20/3) куб.ед.

Высота h пирамиды ABCD, опущенная из вершины D на плоскость основания ABC, равна: h = 3V/S(ABC).

Площадь основания АВС равна половине модуля векторного произведения АВ х АС.

S(ABC) = (1/2)*√((-5)² + (-10)² + 0²) = (1/2)√(25 + 100) = (5/2)√5 кв.ед.

h = (3*20/3)/((5/2)√5) = 8/√5 = 8√5/5 ≈ 3,5777.

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

A ( ; ; ), B ( ; ; ),
C ( ; ; ), D ( ; ; )

Примечание: дробные числа записывайте
через точку, а не запятую.

[spoiler title=”источники:”]

http://reshimvse.com/zadacha.php?id=22499

http://dudom.ru/kompjutery/kak-najti-vysotu-piramidy-po-vektoram/

[/spoiler]

Высота, проведенная к стороне АС, перпендикулярна к стороне АС по определению. Значит вектор высоты, обозначим его Х (х1,х2), должен быть перпендикулярным к вектору АС.

В качестве вектора высоты Х можно взять вектор
Х (с2-а2, -с1+а1). Чтобы проверить, что этот вектор перпендикулярен к вектору АС, надо посчитать скалярное произведение.
Получаем:
(с1-а1)*(с2-а2) + (с2-а2)*(-с1+а1) = 0
Раз скалярное произведение равно нулю, значит векторы перпендикулярны, что нам и нужно.

вектор a(2, -1, 1) вектор b (0, 4, 1)

задан 27 Янв ’14 18:40

Длины векторов легко находятся. Далее через скалярное произведение выражаем косинус угла. Зная косинус, находим синус. Через синус и длины выражаем площадь. Длина разности векторов — это противолежащая сторона. Поделив на неё удвоенную площадь, находим длину высоты.

Здравствуйте

Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

И в итоге: x+2y+z-9=0
это вы написали уравнение плоскости, проходящей через точку С перпендикулярно АВ.

Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости

I. «Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости»

Нужно найти не длину, а уравнение CH.

II. «Можно воспользоваться двойным векторным произведением. и найти направляющий вектор высоты. »
То есть:
AC<2,2,2>
AB

Нужно найти не длину, а уравнение CH. — Если найдёте `H`, то сможете написать уравнение по двум точкам.

Так? — Да. только вычисления не проверял. а в том, что получили, можно сократить на 36.

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---

---

---

---

---

---

---

---

Как найти высоту треугольника, если даны координаты точек

Высотой в треугольнике называют отрезок прямой линии, соединяющий вершину фигуры с противолежащей стороной. Этот отрезок обязательно должен быть перпендикулярен стороне, поэтому из каждой вершины можно провести лишь одну высоту. Поскольку вершин в этой фигуре три, высот в нем столько же. Если треугольник задан координатами своих вершин, вычисление длины каждой из высот можно произвести, например, воспользовавшись формулой нахождения площади и рассчитав длины сторон.

Инструкция

Исходите в расчетах из того, что площадь треугольника равна половине произведения длины любой из его сторон на длину высоты, опущенной на эту сторону. Из этого определения вытекает, что для нахождения высоты нужно знать площадь фигуры и длину стороны.

Начните с вычисления длин сторон треугольника. Обозначьте координаты вершин фигуры так: A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) и C(X₃,Y₃,Z₃). Тогда длину стороны AB вы сможете рассчитать по формуле AB = √((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²). Для двух других сторон эти формулы будут выглядеть так: BC = √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²) и AC = √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²). Например, для треугольника с координатами A(3,5,7), B(16,14,19) и C(1,2,13) длина стороны AB составит √((3-16)² + (5-14)² + (7-19)²) = √(-13² + (-9²) + (-12²)) = √(169 + 81 + 144) = √394 ≈ 19,85. Длины сторон BC и AC, рассчитанные таким же способом, будут равны √(15² + 12² + 6²) = √405 ≈ 20,12 и √(2² + 3² + (-6²)) = √49 = 7.

Знания длин трех сторон, полученных на предыдущем шагу, достаточно для вычисления площади треугольника (S) по формуле Герона: S = ¼ * √((AB+BC+CA) * (BC+CA-AB) * (AB+CA-BC) * (AB+BC-CA)). Например, после подстановки в эту формулу значений, полученных из координат треугольника-образца из предыдущего шага, эта формула даст такое значение: S = ¼*√((19,85+20,12+7) * (20,12+7-19,85) * (19,85+7-20,12) * (19,85+20,12-7)) = ¼*√(46,97 * 7,27 * 6,73 * 32,97) ≈ ¼*√75768,55 ≈ ¼*275,26 = 68,815.

Исходя из площади треугольника, рассчитанной на предыдущем шаге, и длин сторон, полученных на втором шаге, вычислите высоты для каждой из сторон. Так как площадь равна половине произведения высоты на длину стороны, к которой она проведена, для нахождения высоты делите удвоенную площадь на длину нужной стороны: H = 2*S/a. Для использованного выше примера высота, опущенная на сторону AB составит 2*68,815/16,09 ≈ 8,55, высота к стороне ВС будет иметь длину 2*68,815/20,12 ≈ 6,84, а для стороны АС эта величина будет равна 2*68,815/7 ≈ 19,66.

Источники:

• даны точки найти площадь треугольника

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Уравнение высоты треугольника по координатам его вершин

Чтобы составить уравнение высоты треугольника по координатам его вершин нужно:

1. Составить уравнение прямой, на которой лежит высота треугольника:

Так как высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону, то угловые коэффициенты перпендикулярных прямых связаны записанной выше пропорцией.

Уравнение высоты треугольника по координатам его вершин

Составить уравнение высоты треугольника. Пример

Дан треугольник АВС. Вершины треугольника имеют следующие координаты:

На сторону АС опущена высота ВН.

Составить уравнение высоты ВН.

Пример на составление уравнения высоты треугольника

Шаг 1

Составим уравнение прямой, проходящей через точки А и С.

Для этого воспользуемся уравнением прямой с угловым коэффициентом:

Подставим в это уравнение координаты точек А и С:

Уравнение стороны АС имеет вид:

Составить уравнение высоты треугольника. Шаг 1

Шаг 2

Так как прямые АС и ВН перпендикулярны, то, зная угловой коэффициент прямой АС, можем составить уравнение прямой ВН с угловым коэффициентом.

Итак, угловой коэффициент АС равен:

Отсюда, угловой коэффициент ВН будет равен:

Теперь можем записать уравнение высоты ВН:

Точка В(2,4) лежит на прямой ВН, значит, ее координаты удовлетворяют уравнению прямой ВН:

Таким образом, уравнение высоты ВН имеет вид:

Составить уравнение высоты треугольника. Шаг 2

Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач

Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.

Угол наклона прямой и угловой коэффициент прямой

Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.

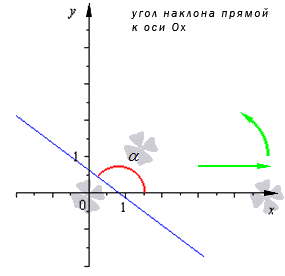
Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.

Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .

Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.

Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.

Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.

Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.

Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .

Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .

Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .

Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .

Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .

Ответ: α = a r c t g 3 .

Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .

Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:

α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .

Ответ: 5 π 6 .

Уравнение с угловым коэффициентом

Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .

Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.

Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.

Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.

Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.

Ответ: М 1 принадлежит прямой, а М 2 нет.

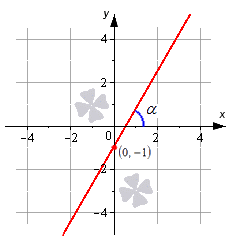
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .

Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку

Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .

Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .

Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .

Решение

По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .

Ответ: y = — 2 x + 7 .

Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .

По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:

y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно

Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.

Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .

Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.

Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.

Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:

y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3

Ответ: x 1 = y — 12 — 3 .

Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.

Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?

Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:

y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0

Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .

Решим задачу обратную данной.

Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .

Результат и является уравннием с угловым коэффициентом, который равняется — A B .

Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.

Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:

2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .

Ответ: y = 1 6 x + 1 4 .

Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:

x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .

Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1

Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.

Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:

y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .

Ответ: y = 3 2 x — 3 .

Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.

Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:

5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x

Ответ: y = 5 2 x — 6 .

Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.

Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .

Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:

x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .

Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:

x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1

Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .