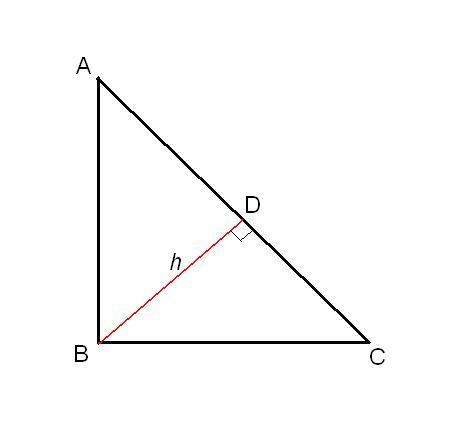
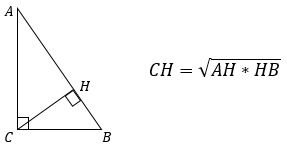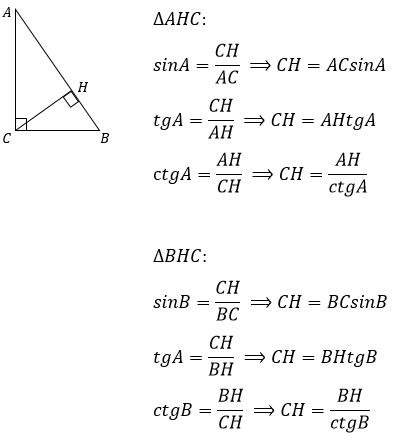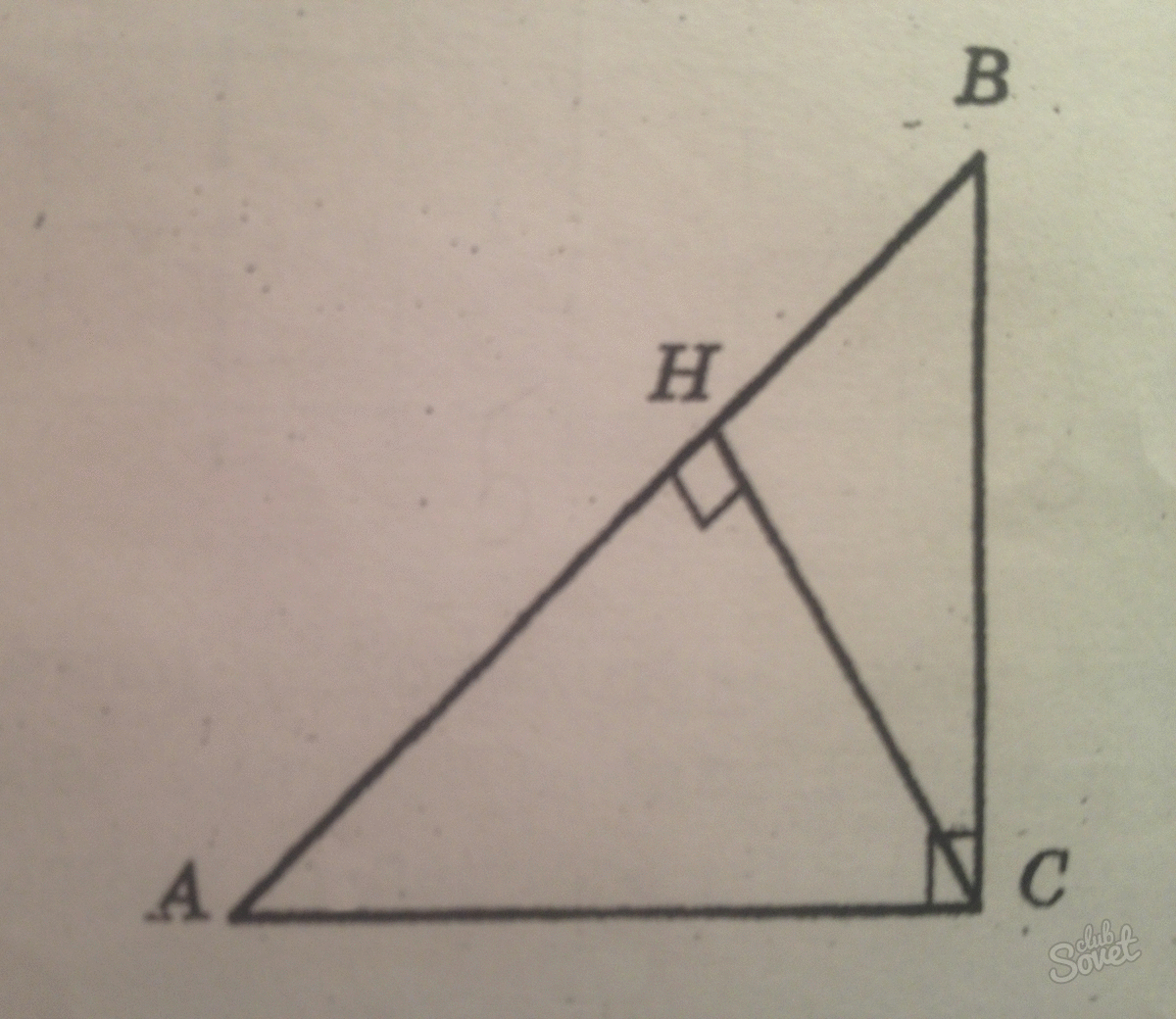В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.
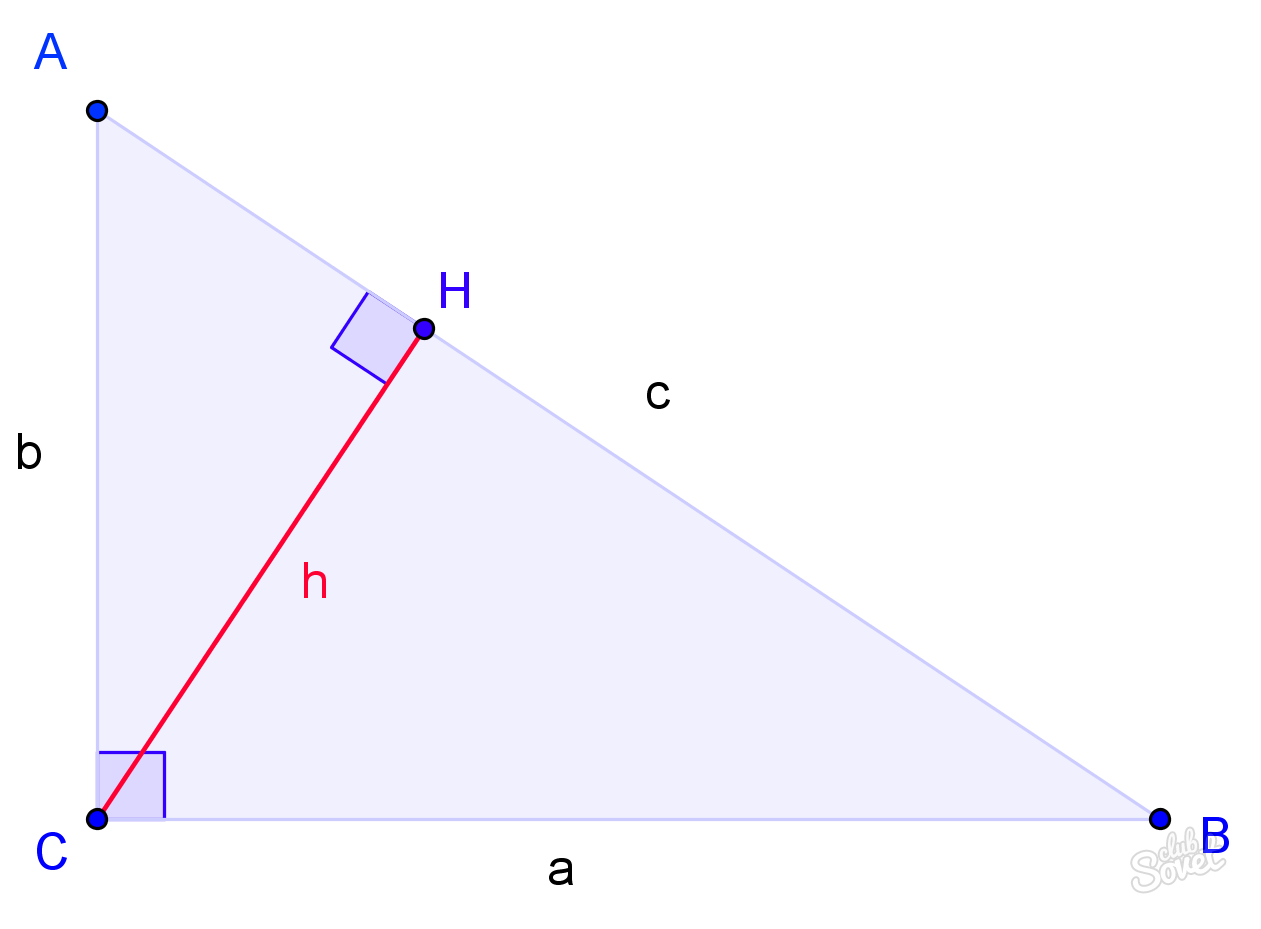
H – высота из прямого угла
a, b – катеты
с – гипотенуза
c1 , c2 – отрезки полученные от деления гипотенузы, высотой
α, β – углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
- Подробности
-
Опубликовано: 09 октября 2011
-
Обновлено: 13 августа 2021
Naumenko
Высший разум
(856096)
12 лет назад
ответ Сергея неверный.
сделайте так:
1. по т. Пифагора найдите второй катет.
2. высота. проведенная к гипотенузе, может быть найдена, если разделить произведение катетов на гипотенузу.
точно-точно!!!!
Ириск@
Знаток
(252)
12 лет назад
по теореме пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
a(квадрат) + b(квадрат) = c(квадрат)
Высота прямоугольного треугольника, проведенная к гипотенузе
Как и в любом треугольнике прямоугольный треугольник имеет три высоты. Две из них совпадают с катетами, а вот третья высота, проведенная к гипотенузе, постоянно будоражит наши умы.
Поэтому представляю вашему вниманию основные формулы для ее нахождения.
Начну с самой важной.
1. Высота, проведенная к гипотенузе равна корню квадратному из произведения проекций катетов на эту гипотенузу.
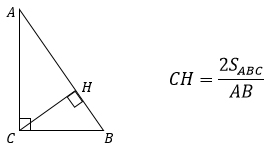
2. Высоту, проведенную к гипотенузе, можно найти, разделив удвоенную площадь прямоугольного треугольника на гипотенузу.
Такая формула получается из классический формулы нахождения площади треугольника: половина произведения основания на высоту, проведенную к этому основанию.
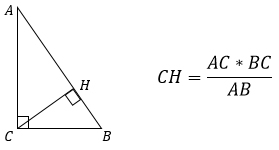
3. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на гипотенузу.
Эта формула получится из второй если заменить площадь на половину произведения катетов.
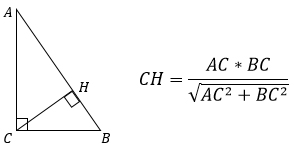
Т.к. АВ – гипотенуза, то ее можно выразить через катеты АС и ВС, используя теорему Пифагора. Тогда формула примет другой вид:
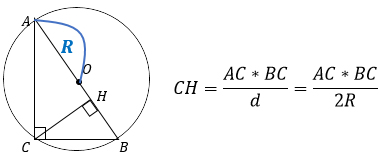
4. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на диаметр описанной вокруг треугольника окружности (или на удвоенный радиус).
Так получается потому, что центр описанной окружности лежит в середине гипотенузы, значит, гипотенуза равна 2R или d.
5. Высоту, проведенную к гипотенузе, можно найти, используя геометрические определения синуса, тангенса и котангенса.
Надеюсь, что данная статья оказалась полезной!)
Готовься к экзамену вместе с нами! Заходи на нашу страницу в ВК.
Как найти высоту в прямоугольном треугольнике
Высота—перпендикуляр, исходящий из вершины треугольника и проведенный до его противоположной стороны. Метод для решения задачи по нахождению высоты в прямоугольном треугольнике следует выбирать в зависимости от условия.
1
Найти высоту в прямоугольном треугольнике через формулу произведения
Если известны длины частей (или их соотношение), на которые высота делит гипотенузу, то найти её можно через произведение длин отрезков этих отрезков.
Формула расчета высоты:
CH=√BH*HA
2
Найти высоту в прямоугольном треугольнике через площадь треугольника
- Если по условию известна площадь треугольника, то можно без труда выразить формулу вычисления высоты: частное удвоенной площади треугольника и гипотенузы:
CH=2S/AB
CH—высота, S—площадь треугольника, AB—гипотенуза
- Также эту формулу можно записать в виде частного произведения катетов и гипотенузы:
CH=AC*BC/AB
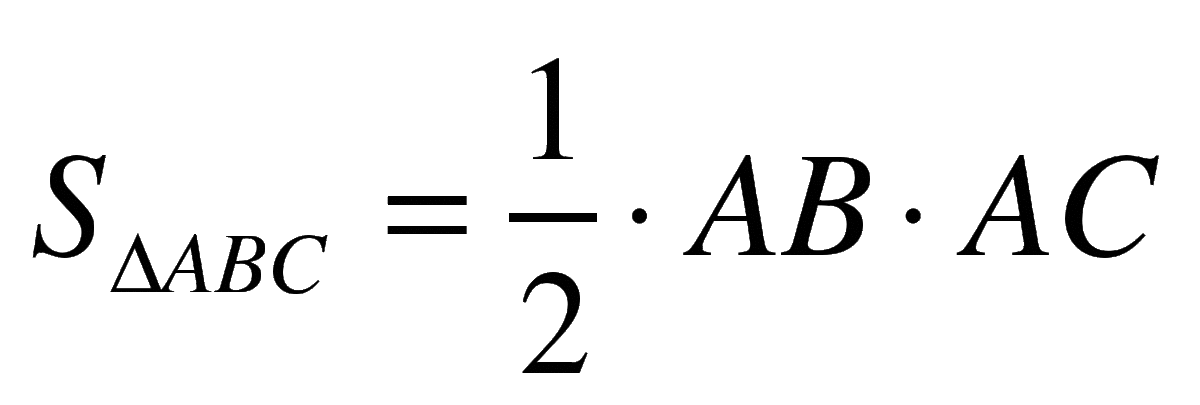
3
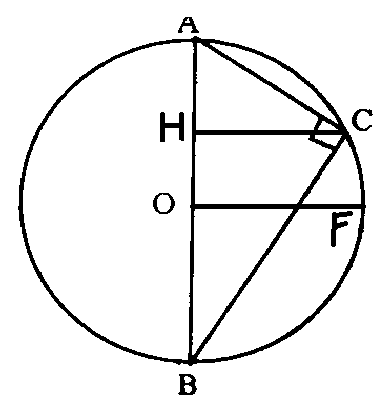
Найти высоту в прямоугольном треугольнике через радиус описанной окружности
Если вокруг треугольника описана окружность, известен её радиус, то высоту можно рассчитать с помощью формулы частного произведения катетов и удвоенного радиуса окружности.
HC=AC*CB/2FO
4
Найти высоту в прямоугольном треугольнике через синус угла
- Высоту можно найти, если умножить синус одного из острых углов на прилежащий катет.
Так выглядит формула:
h=AB* sin A
- Еще один вариант: умножаем отрезок гипотенузы на тангенс прилежащего острого угла.
h=DC*tg C
Используя данные формулы можно достаточно легко отыскать высоту прямоугольного треугольника. Знания о нахождении высоты часто используются в решении многих геометрических задач, поэтому это одни из самых базовых формул геометрии.
Как найти высоту в прямоугольном треугольнике, если известна только гипотенуза?
Найдите правильный ответ на вопрос ✅ «Как найти высоту в прямоугольном треугольнике, если известна только гипотенуза? …» по предмету 📘 Геометрия, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Дано треугольник OBS угол B=90 градусов угол S=45 градусов OB=1008 СМ Найти SB
Ответы (1)
Дано abcd-параллелограмм, BCA=31 градусов, BAC=25 градусов
Ответы (1)
Один угол параллелограмма в 4 разОдин угол параллелограмма в 4 раза больше другого. Найдите больший угол. Ответ дайте в градусах. а больше другого. Найдите больший угол.
Ответы (1)
NK на 19 см. больше MN, MK = 81 см. Найти : MK, NK
Ответы (1)
Начертите угол AOB и лучи ОК и ОМ, проходящие между сторонами этого угла, так, чтобы угол AOB = 90, AOK = 40, MOB = 30, Найдите KOM
Ответы (1)
Главная » Геометрия » Как найти высоту в прямоугольном треугольнике, если известна только гипотенуза?