|
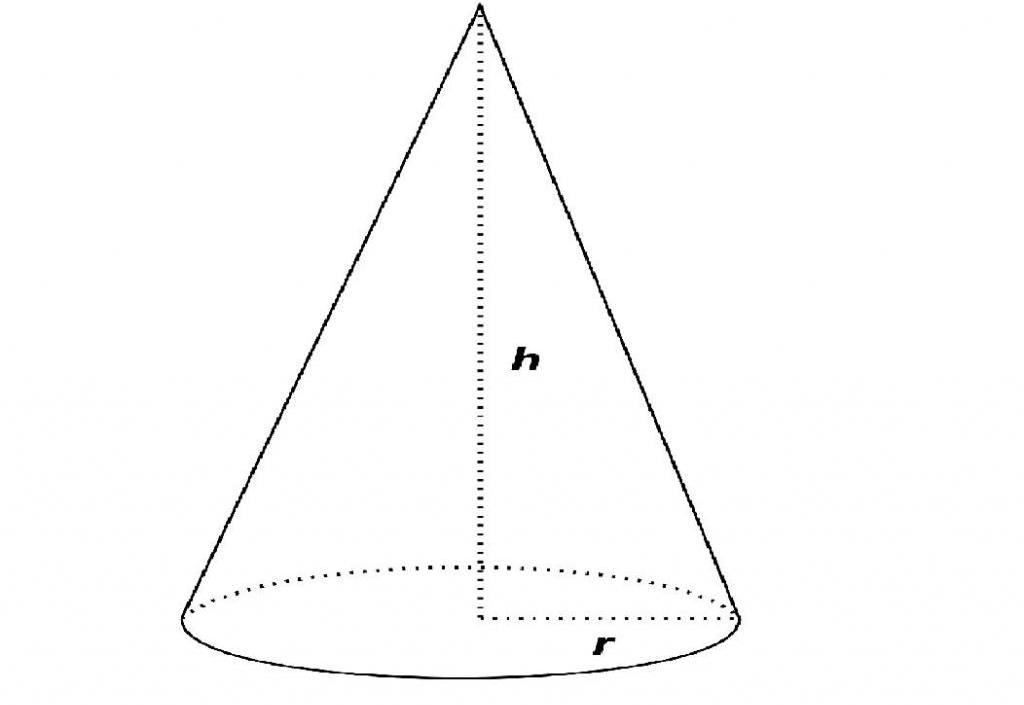
Длина отрезка линии опушенной перпендикулярно плоскости основания из вершины конуса является его высотой. Найти не сложно. Для этого нужно знать величину конуса. Если конус велик и внутри его полость, то достаточно опустить из вершины нитку с грузом до основания и измерить длину нитки. Если конус мал и умещается в руках, то достаточно измерить боковую сторону и ширину основания. Половина основания – это один катет. Боковая сторона гипотенуза. А высотой окажется другой катет воображаемого прямоугольного треугольника. К сожалению тут нарисовать не где. Далее, зная значения катета и гипотенузы по теореме Пифагора находим другой катет – высоту конуса. Если конус не симметричный и вершина сдвинута относительно середины, то для расчетов нужно знать угол между плоскостью основания и боковой стороной в месте их измерения. Далее геометрия… Формулы есть в любом справочнике. автор вопроса выбрал этот ответ лучшим Ксарфакс 5 лет назад Высота конусаЭто перпендикуляр, который опущен из вершины конуса на основание. Чтобы найти высоту конуса можно воспользоваться несколькими способами. 1) Если известно, чему равен объём конуса, то высоту можно вычислить по формуле: V = 1/3 Sосн * h -> h = 3V / Sосн. При этом для нахождения площади основания (площади круга) нам нужно знать радиус. 2) Образующая конуса, высота и радиус основания образуют прямоугольный треугольник. Поэтому если известна образующая (гипотенуза) и радиус (катет), то высоту можно выразить с помощью теоремы Пифагора. a² = c² – b², a = √(c² – b²). a – высота, b – радиус, c – образующая. Например: Радиус основания = 15 см, длина образующей – 17 см. Высота конуса будет равна √(17² – 15²) = √64 = 8 см. -Irinka- 4 года назад Для того, чтобы найти высоту конуса, необходимо иметь для решения какие-то вводные. Допустим, что мы знаем длина образующей конуса, она равна 10 см. и диаметр его основания равный 12 см. Находим радиус конуса R=D/2= 6 см. Вот наш конус, чертим нужные нам линии. Используем теорему Пифагора, получаем h²=a²-R², где а – длина образующей конуса (10 см), h искомая высота. h² = 100 – 36 = 64 h = √64 = 8 сантиметров Alexgroovy 5 лет назад Для поиска высоты конуса нужны входные данные. В качестве таких данных выступает радиус (или диаметр основания) и длина образующей конуса. На рисунке длина образующей обозначена буквой l, а диаметр основания как d. Например, по условию задачи l = 100, d = 56. Решение задачи будет следующим: 88SkyWalker88 5 лет назад Начертим конус, проведем его высоту и основание: Нам известна величина l – это образующая. Она равна 16. Угол между основанием и образующий будет равняться 30 градусам. У нас получился прямоугольный треугольник, в котором образующая (l) – это гипотенуза, а высота (h), которую нам необходимо найти, это катет. Так как нам известен угол, мы можем найти его синус. sin 30° = ½ Известно, что синус – это отношение противолежащего катета к гипотенузе. Следовательно, можно составить такую формулу: sin 30° = h/l = ½ Из этой формулы мы выводим h, высоту конуса. Получается формула и решение: h = sin 30°*l = ½ * 16 = 8. Чосик более года назад Зависит от данных, которые мы получили изначально. Для того, чтобы узнать высоту, необходимо знать радиус и апофему. В таком случае мы получим прямоугольный треугольник, где высота и радиус играют роль катетов, а апофема – гипотенузы. Если же мы знает площадь основания и объем конуса, то высота равна h = 3V/S. владсандрович более года назад Высоту конуса можно найти разными формулами, тут все зависит от того, что вам известно. В частности если известны площадь его основания и объем самого конуса, то тогда все просто, так как данные значения надо подставить под формулу h = 3V/S и просто посчитать. JuliGor 9 лет назад Если известны объем и площадь конуса, то высоту легко найти, так как объем конуса равен одной трети площади основания умноженная на высоту конуса. Также высоту конуса можно найти по теореме Пифагора, но это по-моему гораздо сложнее) moreljuba 5 лет назад Высоту конуса мы можем выразить из формулы, по которой мы определяем объём конуса: Так вот высота конуса из данной формулы будет равна: Высота конуса = 3 * объём конуса / пи * радиус основания в квадрате. Знаете ответ? |
Используя равнобедренный треугольник, где в качестве сторон выступают диаметр основания и образующие по обеим его сторонами, можно найти угол между образующей и основанием, равный половине разности угла раствора от 180 градусов. Затем через найденный угол с основанием в прямоугольном треугольнике с высотой и радиусом можно вычислить саму образующую и радиус конуса. (рис. 40.2, 40.1)
β=(180°-α)/2
l=h/sinβ
r=cotβ h
Подставив полученное значение радиуса в формулы основания, такие как диаметр, периметр и площадь, найдем их через угол и высоту конуса.
d=2r=2 cotβ h
P=2πr=2π cotβ h
S_(осн.)=πr^2=πh^2 cot^2β
Чтобы вычислить площадь боковой поверхности через угол раствора и высоту конуса необходимо воспользоваться полученным углом между образующей и основанием и тригонометрическими отношениями для радиуса и образующей конуса, подставив их в нужные формулы.
S_(б.п.)=πrl=π ( cotβ h^2)/sinβ =πh^2 cosβ
S_(п.п.)=S_(б.п.)+S_(осн.)=πh^2 (cosβ+cot^2β )
Объем конуса стандартно выражен через площадь основания и высоту, разделенные на три. Так как площадь основания равна произведению числа π на квадрат высоты и квадрат котангенса угла β, то необходимо подставить это выражение в формулу вместо площади, чтобы найти объем через угол раствора и высоту.
V=(hS_(осн.))/3=(πh^3 cot^2β)/3
Радиусы вписанной и описанной сфер около конуса могут быть найдены с использованием угла раствора и угла при основании конуса с тем небольшим изменением в формулах, что вместо радиуса будет подставлено произведение высоты на котангенс угла наклона. (рис.40.3, 40.4)
r_1=r tan〖β/2〗=h cotβ tan〖β/2〗
R=r/sinα =(cotβ h)/sinα
Прочитав данную статью, вы узнаете, как найти высоту конуса. Приведенный в ней материал поможет глубже разобраться в вопросе, а формулы окажутся весьма полезными в решении задач. В тексте разобраны все необходимые базовые понятия и свойства, которые обязательно пригодятся на практике.
Фундаментальная теория
Перед тем, как найти высоту конуса, необходимо разобраться с теорией.
Конус – фигура, которая плавно сужается от плоского основания (часто, хотя и необязательно, кругового) до точки, называемой вершиной.
Конус формируется набором отрезков, лучей или прямых, соединяющих общую точку с основанием. Последнее может ограничиваться не только окружностью, но и эллипсом, параболой или гиперболой.
Ось – это прямая (если таковая имеется), вокруг которой фигура имеет круговую симметрию. Если угол между осью и основой составляет девяносто градусов, то конус принято называть прямым. Именно такая вариация чаще всего встречается в задачах.
Если в основе лежит многоугольник, то объект является пирамидой.
Отрезок, соединяющий вершину и линию, ограничивающую основание, называют образующей.
Как найти высоту конуса
Подойдем к вопросу с другой стороны. Для начала используем объем конуса. Чтобы его найти нужно вычислить произведение высоты с третьей частью площади.
V = 1/3 × S × h.
Очевидно, что из этого можно получить формулу высоты конуса. Достаточно лишь сделать правильные алгебраические преобразования. Разделим обе части равенства на S и умножим на тройку. Получим:
h = 3 × V × 1/S.
Теперь вы знаете, как найти высоту конуса. Однако для решения задач вам могут понадобиться и другие знания.
Важные формулы и свойства
Приведенный ниже материал однозначно поможет вам в решении конкретных задач.
Центр массы тела находится на четвертой части оси, начиная от основы.
В проективной геометрии цилиндр – это просто конус, вершина которого находится на бесконечности.
Следующие свойства работают только для прямого кругового конуса.
- Даны радиус основания r и высота h, тогда формула для площади будет выглядеть так: П × r2. Соответственно изменится и окончательное уравнение. V = 1/3 × П × r2 × h.
- Вычислить площадь боковой поверхности можно перемножив число “пи”, радиус и длину образующей. S = П × r × l.
- Пересечение произвольной плоскости с фигурой является одним из конических сечений.
Часто встречаются задачи, где необходимо использовать формулу для объема усеченного конуса. Она выводится из обычной и имеет такой вид:
V = 1/3 × П × h × (R2 + Rr + r2), где: r -радиус нижнего основания, R – верхнего.
Всего этого будет вполне достаточно для решения разнообразнейших примеров. Разве что могут понадобиться знания, не связанные с этой темой, например, свойства углов, теорема Пифагора и другое.
Узнаем как найти высоту конуса. Теория и формулы
Прочитав данную статью, вы узнаете, как найти высоту конуса. Приведенный в ней материал поможет глубже разобраться в вопросе, а формулы окажутся весьма полезными в решении задач. В тексте разобраны все необходимые базовые понятия и свойства, которые обязательно пригодятся на практике.
Фундаментальная теория
Перед тем, как найти высоту конуса, необходимо разобраться с теорией.
Конус — фигура, которая плавно сужается от плоского основания (часто, хотя и необязательно, кругового) до точки, называемой вершиной.
Конус формируется набором отрезков, лучей или прямых, соединяющих общую точку с основанием. Последнее может ограничиваться не только окружностью, но и эллипсом, параболой или гиперболой.
Ось — это прямая (если таковая имеется), вокруг которой фигура имеет круговую симметрию. Если угол между осью и основой составляет девяносто градусов, то конус принято называть прямым. Именно такая вариация чаще всего встречается в задачах.
Узнаем как посчитать объем — формулы расчета
В статье речь идет о способах определения объема различных тел, прикладных задачах, связанных с…
Если в основе лежит многоугольник, то объект является пирамидой.
Отрезок, соединяющий вершину и линию, ограничивающую основание, называют образующей.
Как найти высоту конуса
Подойдем к вопросу с другой стороны. Для начала используем объем конуса. Чтобы его найти нужно вычислить произведение высоты с третьей частью площади.
V = 1/3 × S × h.
Очевидно, что из этого можно получить формулу высоты конуса. Достаточно лишь сделать правильные алгебраические преобразования. Разделим обе части равенства на S и умножим на тройку. Получим:
h = 3 × V × 1/S.
Теперь вы знаете, как найти высоту конуса. Однако для решения задач вам могут понадобиться и другие знания.
Важные формулы и свойства
Приведенный ниже материал однозначно поможет вам в решении конкретных задач.
Центр массы тела находится на четвертой части оси, начиная от основы.
В проективной геометрии цилиндр — это просто конус, вершина которого находится на бесконечности.
Следующие свойства работают только для прямого кругового конуса.
- Даны радиус основания r и высота h, тогда формула для площади будет выглядеть так: П × r2. Соответственно изменится и окончательное уравнение. V = 1/3 × П × r2 × h.
- Вычислить площадь боковой поверхности можно перемножив число «пи», радиус и длину образующей. S = П × r × l.
- Пересечение произвольной плоскости с фигурой является одним из конических сечений.
Часто встречаются задачи, где необходимо использовать формулу для объема усеченного конуса. Она выводится из обычной и имеет такой вид:
V = 1/3 × П × h × (R2 + Rr + r2), где: r -радиус нижнего основания, R — верхнего.
Всего этого будет вполне достаточно для решения разнообразнейших примеров. Разве что могут понадобиться знания, не связанные с этой темой, например, свойства углов, теорема Пифагора и другое.
Как найти объем прямого кругового конуса: формулы
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение объема конуса: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать объем прямого кругового конуса и разберем примеры решения задач.
-
Формула вычисления объема
- 1. Через площадь основания и высоту
- 2. Через радиус основания и высоту
- Примеры задач
Формула вычисления объема
1. Через площадь основания и высоту
Объем (V) конуса равняется одной третьей произведения его высоты на площадь основания:
2. Через радиус основания и высоту
Как мы знаем, основанием конуса является круг, площадь которого вычисляется по формуле: S = πR2.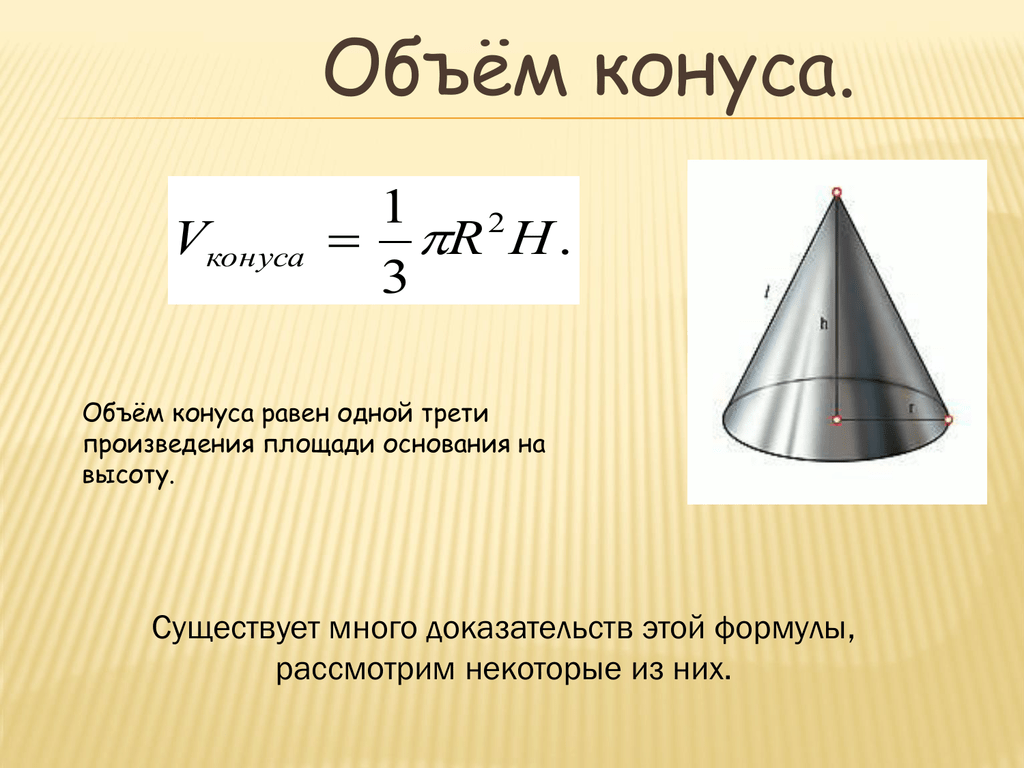
Следовательно, формулу для вычисления объема конуса можно представить в виде:
Т.е. объем конуса равняется одной третьей произведения его высоты на число π и на радиус основания в квадрате.
Примечание: в расчетах значение числа π округляется до 3,14.
Формула для нахождения объема усеченного конуса представлена в отдельной публикации.
Примеры задач
Задание 1
Найдите объем конуса, если известна площадь его основания – 50,24 см2, а также, высота – 9 см.
Решение:
Применим первую формулу, подставив в нее заданные значения:
Задание 2
Высота конуса равна 7 см, а его радиус – 3 см. Найдите объем фигуры.
Решение:
Воспользовавшись второй, более расширенной, формулой получаем:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Калькулятор высоты конуса
Создано Luciano Mino
Отзыв от Davide Borchia
Последнее обновление: 09 мая 2022 г.
Калькулятор высоты конуса поможет вам найти высоту любого конуса по двум параметрам .
Здесь вы узнаете:
- Как найти высоту конуса, зная его объем и радиус .
- Как найти высоту конуса без его объема, зная его радиус и наклонную высоту .
Пропорционален ли радиус конуса его высоте? Продолжайте читать, чтобы узнать ответ на этот вопрос, и прочитайте несколько примеров высоты конуса!
Определение конуса
Конус представляет собой трехмерную форму с круглым основанием и единственной вершиной, называемой вершиной . Это самый интуитивно понятный конус для воображения (например, дорожные конусы или мороженое).
Калькулятор высоты конуса работает с конусами, вершина которых расположена непосредственно над центром его основания. Они называются правильными круговыми конусами . Конусы с вершиной не выше центра основания называются косыми конусами 9{2}}h=π×r23×V
Посмотрим, когда применять каждое следующее.
Как найти высоту конуса, не зная его объема?
Чтобы найти высоту конуса, не зная его объема:
- Запишите радиус и наклонную высоту размеры.
- Введите их в формулу высоты конуса:
h = √(l² - r²)где:-
l— высота наклона; -
р— радиус; и -
h– результирующая высота.
-
- Вот так !
Как найти высоту конуса, зная его объем?
Чтобы найти высоту конуса, зная его радиус и объем:
- Запишите радиус и объем .
- Введите их в высоту конуса формула объема:
h = 3 × V/(π × r²)где:-
V— объем конуса; -
r— радиус; и -
h– результирующая высота.
-
- Это так просто !
Примеры с использованием калькулятора высоты конуса
Пример 1. Нахождение высоты по радиусу и наклонной высоте
Допустим, мы хотим найти высоту конуса с радиусом r=5 cmr = 5 text{cm} r=5 см и наклонная высота l=8 смl = 8 text{см}l=8 см. Тогда мы используем формулу высоты конуса без объема: 9{2}} \
h &=sqrt{39} ≈ 6,25 text{см}
end{align*}hh=(8 cm)2−(5 cm)2
=39
≈6,25 cm
объем конуса радиусом 20 см20 text{см}20 см равен V=1 L=1000 см³V = 1 text{L} = 1000 text{см³}V=1 L=1000 см³.
Глядя на формулу из предыдущего раздела, мы знаем, что высота будет равна:
h=3×1000 см³π×(20 см)2h≈2,39 смbegin{align*}
h &= frac{3 times 1000 text{cm³}}{pi times(20 text{cm})^{2}} \\
ч & ≈ 2,39 текст{см}
end{align*}hh=π×(20 cm)23×1000 cm³≈2,39 cm
Другие подобные инструменты
Обязательно ознакомьтесь с другими нашими калькуляторами, похожими на калькулятор высоты конуса!
- Правый круговой конус
- Радиус конуса
- Боковая часть конуса
- Наклонная высота конуса, а
- Диаметр конуса.
Часто задаваемые вопросы
Пропорционален ли радиус конуса его высоте?
№ . Радиус конуса и высота конуса не зависят друг от друга, если нет фиксированных переменных (например, объема конуса). Однако высота конуса и радиус прямо пропорциональны размеру его наклонной высоты.
Какова высота конуса с радиусом 10 см и высотой наклона 15 см?
5√5 = 11,18 . Чтобы найти высоту конуса 10 см радиуса и 15 см высоты наклона, вам нужно ввести эти параметры в формулу высоты конуса h = √(l² - r²) , где:
-
l— высота наклона конуса; и -
rэто радиус.
Лучано Миньо
Радиус (r)
Наклонная высота (l)
Объем (V)
Высота (h)
Посмотреть 21 похожий калькулятор 3d геометрии 📦
Площадь полушарияCubeCube Рассчитать: найти v, a, d… еще 18
Наклонная высота прямого конуса
Наклонная высота прямого конуса — Открытый справочник по математике
Открытый справочник по математике
Главная
Контакт
О
Тематический указатель
Определение:
Расстояние от вершины конуса вниз по стороне до точки на краю основания.
Попробуйте это
Перетащите оранжевые точки, чтобы отрегулировать радиус и высоту конуса, и обратите внимание, как изменится высота наклона.
Есть три измерения конуса.
- Вертикальная высота (или высота), которая является перпендикулярным расстоянием от вершины вниз до основания.
- Радиус круглого основания
- Наклонная высота, которая представляет собой расстояние от верха вниз сбоку до точки на окружности основания.
Эти три связаны, и нам нужны только два, чтобы определить конус. Затем мы можем найти третье недостающее измерение.
На рисунке выше мы видим, что три измерения образуют
прямоугольный треугольник,
с наклонной высотой
гипотенуза,
поэтому мы можем использовать
Теорема Пифагора для ее решения*.
Перетащите любую оранжевую точку на верхнем рисунке и обратите внимание, как высота наклона рассчитывается на основе радиуса и высоты.
* На самом деле мы можем использовать любой метод решения этого треугольника, который нам нравится.
См. Решение треугольника.
Нахождение наклонной высоты
Применяя теорему Пифагора, наклонная высота определяется формулой:
где r — радиус основания, а h — высота.
Если задана высота наклона
Переставляя термины в теореме Пифагора, мы можем решить для других длин:
- Радиус r можно найти по формуле
где s — наклонная высота, h — высота над уровнем моря. - Высоту h можно найти по формуле
где s — высота наклона, r — радиус основания.
Что попробовать
- На верхнем рисунке нажмите «скрыть подробности».
- Перетащите оранжевые точки, чтобы установить радиус и высоту конуса.
- Рассчитайте наклонную высоту конуса по формуле
- Нажмите «показать подробности», чтобы проверить свой ответ.
Похожие темы
- Определение лица
- Определение края
- Том
- Определение и свойства куба
- Объем, заключенный в куб
- Площадь поверхности куба
- Определение и свойства пирамиды
- Косые и правые пирамиды
- Объем пирамиды
- Площадь поверхности пирамиды
- Цилиндр – определение и свойства
- Цилиндр относительно призмы
- Цилиндр как геометрическое место линии
- Наклонные цилиндры
- Объем цилиндра
- Объем частично заполненного цилиндра
- Площадь поверхности цилиндра
- Размер призмы
- Объем призмы
- Площадь поверхности призмы
- Объем сферы
- Площадь поверхности сферы
- Определение конуса
- Наклонный и правый конусы
- Объем конуса
- Площадь поверхности конуса
- Вывод формулы площади конуса
- Высота наклона конуса
- Конические профили — круг
- Конические профили — эллипс
- Икосаэдр (20 граней равностороннего треугольника)
(C) 2011 Copyright Math Open Reference.
Онлайн-калькулятор
Общее определение конуса
Конус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.
Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.
Рассмотрим некоторые важные понятия.
Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной. Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.
Конус бывает нескольких типов:
Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.
Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.
Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.
Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.
Свойства кругового конуса
Выделяют несколько особенностей, которыми обладает фигура данного типа:
- Образующие кругового конуса равны друг другу.
- Чтобы найти центр тяжести фигуры, нужно её высоту поделить на четыре части.
- Место пересечения плоскости сечения и основы образует параболу. Если через вершину тела провести плоскость сечения, то получится равнобедренный треугольник.
Интересный факт!
Если вращать прямоугольный треугольник вокруг одного из катетов, то получится конус. При этом важно, чтобы угол вращения был не менее 360 градусов.
Связанные определения для конуса
Образующая конуса. Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
Образующая поверхность конуса. Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.
Коническая поверхность. Образующая поверхность конуса является конической поверхностью.
Высота конуса (H). Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.
Угол раствора конуса. Угол раствора конуса – угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
Прямой конус. Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется осью конуса.
Косой (наклонный) конус. Косой (наклонный) конус – конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
Круговой конус. Круговой конус – конус, основание которого является кругом.
Прямой круговой конус. Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).
Эллиптическим конус. Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
Усечённый конус. Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.
Виды конусов
- Прямой конус – имеет симметричное основание. Ортогональная проекция вершины данной фигуры на плоскость основания совпадает с центром этого основания.
- Косой (наклонный) конус – ортогональная проекция вершины фигуры на ее основание не совпадает с центром этого основания.
- Усеченный конус (конический слой) – часть конуса, которая остается между его основанием и секущей плоскостью, параллельной данному основанию.
- Круговой конус – основанием фигуры является круг. Также бывают: эллиптический, параболический и гиперболический конусы.
- Равносторонний конус – прямой конус, образующая которого равняется диаметру его основания.
Объем конуса
Объем конуса
равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
где V – объем конуса, So – площадь основания конуса, R – радиус основания конуса, h – высота конуса, π = 3.141592.
Вариации и обобщения
- В алгебраической геометрии конус
— это произвольное подмножество K {displaystyle K} векторного пространства V {displaystyle V} над полем F {displaystyle F} , для которого для любого λ ∈ F {displaystyle lambda in F} λ K = K . {displaystyle lambda K=K.} - В топологии конус над топологическим пространством X
есть фактор-пространство X × [ 0 , ∞ ) {displaystyle Xtimes [0,infty )} по отношению эквивалентности ( x , 0 ) ∼ ( y , 0 ) . {displaystyle (x,0)sim (y,0).}
Объем конуса через радиус
Данный треугольник
для получения конуса должен вращаться вокруг одного из своих
катетов
, который является не только осью вращения, но и высотой конуса.
Второй
же катет становится радиусом полученной в результате вращения окружности-основания конуса, а гипотенуза будет апофемой (высотой опущенной под прямым углом к линии окружности, а не центру).
Технически взаимосвязь конуса
с цилиндром идентична взаимосвязи пирамиды с кубом (параллелепипедом), единственное, что вывод
формулы
проходит через отношения интегралов их сферических углов, но тем не менее, он точно также как и пирамида занимает одну треть цилиндра, в который он может быть вписан.
Поэтому его объем
равен произведению площади основания на высоту, деленному на три, или произведению числом
π
на квадрат радиуса и высоту, деленному на три.
Определение конуса
Далее мы будем рассматривать самый распространенный вид конуса – прямой круговой. Остальные возможные варианты фигуры перечислены в последнем разделе публикации.
Итак, прямой круговой конус – это трехмерная геометрическая фигура, полученная путем вращения прямоугольного треугольника вокруг одного из своих катетов, который в данном случае будет являться осью фигуры. Ввиду этого иногда такой конус называют конусом вращения.
Конус на рисунке выше получен в результате вращения прямоугольного треугольника ACD (или BCD) вокруг катета CD.
Объем усеченного конуса
Усеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом.
Первый способ вычисления объема усеченного конуса
Объем усеченного конуса вычисляется по формуле:
[ LARGE V = frac{1}{3} left( Hcdot S_2 + h cdot s_1 right) ]
где: V – объем конуса h – расстояния от плоскости верхнего основания до вершины H – расстояния от плоскости нижнего основания до вершины S1 – площадь верхнего (ближнего к вершине) основания S2 – площадь нижнего основания
Второй способ вычисления объема усеченного конуса
Объем усеченного конуса вычисляется по формуле:
[ LARGE V = frac{1}{3} pi h left( R^2 + R cdot r + r^2 right) ]
где: V – объем конуса h – высота конуса R – радиус нижнего основания r – радиус верхнего основания
Развёртка
— высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника
r
— радиус в основании конуса. Гипотенузой прямоугольного треугольника является
l
— образующая конуса.
В создании развёртки конуса могут использоваться всего две величины r
и
l
. Радиус основания
r
определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности
l
, являющаяся радиусом сектора боковой поверхности. Угол сектора φ {displaystyle varphi } в развёртке боковой поверхности конуса определяется по формуле:
φ = 360°·(r
/
l
).
Элементы конуса
Определение. Вершина конуса
– это точка (K), из которой исходят лучи.
Определение. Основание конуса
– это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.
Определение. Образующей конуса
(L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.
Формула. Длина образующей
(L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора): L2 = R2 + H2
Определение. Направляющая
конуса – это кривая, которая описывает контур основания конуса.
Определение. Боковая поверхность
конуса – это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.
Определение. Поверхность
конуса состоит из боковой поверхности и основания конуса.
Определение. Высота
конуса (H) – это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.
Определение. Ось
конуса (a) – это прямая, проходящая через вершину конуса и центр основания конуса.
Определение. Конусность (С)
конуса – это отношение диаметра основания конуса к его высоте. В случае усеченного конуса – это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:
где C – конусность, D – диаметр основания, d – диаметр меньшего основания и h – расстояние между основаниями. Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:
где R – радиус основы, а H – высота конуса.
Определение. Осевое сечение
конуса – это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника – это диаметр основания конуса.
Определение. Касательная плоскость
к конусу – это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.
Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим
или
параболическим
конусом (последние два имеют бесконечный объем).
Определение. Прямой
конус – это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.
Формула. Объём кругового конуса
:
где R – радиус основы, а H – высота конуса.
Формула. Площадь боковой поверхности
(Sb) прямого конуса через радиус R и длину образующей L: Sb = πRL
Формула. Общая площадь поверхности
(Sp) прямого кругового конуса через радиус R и длину образующей L: Sp = πRL + πR2
Определение. Косой (наклонный)
конус – это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.
Формула. Объём любого конуса
:
где S – площадь основы, а H – высота конуса.
Определение. Усеченный
конус – это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.
Формула. Объём усеченного конуса
:
где S1 и S2 – площади меньшей и большей основы соответственно, а H и h – расстояние от вершины конуса до центра нижней и верхней основы соответственно.
Основные элементы конуса
- R – радиус круга, являющегося основанием конуса. Центр круга – точка D, диаметр – отрезок AB.
- h (CD) – высота конуса, одновременно являющаяся осью фигуры и катетом прямоугольных треугольников ACD или BCD.
- Точка C – вершина конуса.
- l (CA, CB, CL и CM) – образующие конуса; это отрезки, соединяющие вершину конуса с точками на окружности его основания.
- Осевое сечение конуса – это равнобедренный треугольник ABC, который образуется в результате пересечения конуса плоскостью проходящей через его ось.
- Поверхность конуса – состоит из его боковой поверхности и основания. Формулы для расчета площади поверхности, а также объема прямого кругового конуса представлены в отдельных публикациях.
Между образующей конуса, его высотой и радиусом основания есть взаимосвязь (согласно теореме Пифагора):
l2 = h2 + R2
Развёртка конуса – боковая поверхность конуса, развернутая в плоскость; является круговым сектором.
- длина дуги сектора равняется длине окружности основания конуса (т.е. 2πR);
- α – угол развёртки (или центральный угол);
- l – радиус сектора.
Примечание: Основные свойства конуса мы рассмотрели в отдельной публикации.
Основные свойства кругового конуса
1. Все образующие прямого кругового конуса равны между собой.
2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус.
3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус.
4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус)
5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3).
6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис. 4).
7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение).
8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы.
Определение и элементы конуса
Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние.
При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.
Обратите внимание!
Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.
Хотелось бы рассмотреть ещё несколько понятий по этой теме:
1. Под конусностью понимают отношение диаметра основания фигуры и её высоты:
Важно!
Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.
2. Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:
3. Касательная— это плоскость, которая соприкасается с образующей конуса. При этом важно, чтобы она была перпендикулярна осевому сечению.
Введите радиус основания и высоту конуса
| Радиус конуса r |
| Высота конуса h |
| Результат |
| Расчет объема куба, пирамиды, конуса, цилиндра, шара (объема всех фигур). |
| Объемы фигур |
| Радиус: |
| Высота: |
| Конус – геометрическое тело, которое состоит из круга (основание конуса), точки, не лежащей в плоскости этого круга (вершина конуса), и всех точек, соединяющих вершину конуса с точками основания. Формула объема конуса: , где R – радиус основания, h – высота конуса |
Нормальные углы и конусы инструментов
НОРМАЛЬНЫЕ УГЛЫ ( ГОСТ 8908-81 )
Таблица не распространяется на угловые размеры конусов. При выборе углов 1-й ряд следует предпочитать 2-му, а 2-й — 3-му.
НОРМАЛЬНЫЕ КОНУСНОСТИ и УГЛЫ КОНУСОВ ( ГОСТ 8593-81 )
Стандарт распространяется на конусности и углы конусов гладких конических элементов деталей.
Примечание. Значения конусности или угла конуса, указанные в графе «Обозначение конуса», приняты за исходные при расчете других значений, приведенных в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.
КОНУСЫ ИНСТРУМЕНТОВ УКОРОЧЕННЫЕ ( ГОСТ 9953-82 )
Стандарт распространяется на укороченные инструментальные конусы Морзе.
*z — наибольшее допускаемое отклонение положения основной плоскости, в которой находится диаметр D от теоретическогот положения. ** размеры для справок.
| Обозначение конуса | Конус Морзе | D | D1 | d | d1 | l1 | l2 | a, не более |
b | c |
| B7 | 0 | 7,067 | 7,2 | 6,5 | 6,8 | 11,0 | 14,0 | 3,0 | 3,0 | 0,5 |
| B10 B12 | 1 | 10,094 12,065 | 10,3 12,2 | 9,4 11,1 | 9,8 11,5 | 14,5 18,5 | 18,0 22,0 | 3,5 3,5 | 3,5 3,5 | 1,0 1,0 |
| B16 B18 | 2 | 15,733 17,780 | 16,8 18,0 | 14,5 16,2 | 15,0 16,8 | 24,0 32,0 | 29,0 37,0 | 5,0 5,0 | 4,0 4,0 | 1,5 1,5 |
| B22 B24 | 3 | 21,793 23,825 | 22,0 24,1 | 19,8 21,3 | 20,5 22,0 | 40,5 50,5 | 45,5 55,5 | 5,0 5,0 | 4,5 4,5 | 2,0 2,0 |
| B32 | 4 | 31,267 | 31,6 | 28,6 | — | 51,0 | 57,5 | 6,5 | — | 2,0 |
| B45 | 5 | 44,399 | 44,7 | 41,0 | — | 64,5 | 71,0 | 6,5 | — | 2,0 |
| Размеры D1 и d являются теоретическими, вытекающими соответственно из диаметра D и номинальных размеров а и l1 |
КОНУСНОСТЬ НАРУЖНЫХ И ВНУТРЕННИХ КОНУСОВ И КОНУСОВ С РЕЗЬБОВЫМ ОТВЕРСТИЕМ
| Обозначение величины конуса | Конусность | Угол конуса 2α |
| B7 B10, B12 B16, B18 B22, B24 B32 B45 | 1 : 19,212 = 0,05205 1 : 20,047 = 0,49880 1 : 20,020 = 0,04995 1 : 19,922 = 0,05020 1 : 19,954 = 0,05194 1 : 19,002 = 0,05263 | 2°58′54″ 2°51′26″ 2°51′41″ 2°52′32″ 2°58′31″ 3°00′53″ |
| угол конуса 2α подсчитан по величине конусности с округлением до 1″. |
РЕКОМЕНДУЕМЫЕ РАЗМЕРЫ ЦЕНТРОВОГО ОТВЕРСТИЯ УКОРОЧЕННОГО КОНУСАКОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ НАРУЖНЫЕ ( ГОСТ 25557-2006 )
| Тип конуса | Метрический | Морзе | Метрический | |||||||||||
| Обозн. | 4 | 6 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 80 | 100 | 120 | 160 | 200 |
| D | 4,0 | 6,0 | 9,045 | 9,065 | 17,78 | 23,825 | 31,267 | 44,399 | 63,348 | 80 | 100 | 120 | 160 | 200 |
| D1 | 4,1 | 6,2 | 9,2 | 12,2 | 18,0 | 24,1 | 31,6 | 44,7 | 63,8 | 80,4 | 100,5 | 120,6 | 160,8 | 201,0 |
| d* | 2,9 | 4,4 | 6,4 | 9,4 | 14,6 | 19,8 | 25,9 | 37,6 | 53,9 | 70,2 | 88,4 | 106,6 | 143 | 179,4 |
| d1 | — | — | — | М6 | М10 | М12 | М16 | М20 | М24 | М30 | М36 | М36 | М48 | М48 |
| d4 max |
2,5 | 4,0 | 6,0 | 9,0 | 14,0 | 19,0 | 25,0 | 35,7 | 51,0 | 67,0 | 85,0 | 102,0 | 138,0 | 174,0 |
| l min |
— | — | — | 16,0 | 24,0 | 24,0 | 32,0 | 40,0 | 47,0 | 59,0 | 70,0 | 70,0 | 92,0 | 92,0 |
| l1 | 23,0 | 32,0 | 50,0 | 53,5 | 64,0 | 81,0 | 102,5 | 129,5 | 182,0 | 196,0 | 232,0 | 268,0 | 340,0 | 412,0 |
| l2 | 25,0 | 35,0 | 53,0 | 57,0 | 69,0 | 86,0 | 109,0 | 136,0 | 190,0 | 204,0 | 242,0 | 280,0 | 356,0 | 432,0 |
| l11 | — | — | — | 4,0 | 5,0 | 5,5 | 8,2 | 10,0 | 11,5 | — | — | — | — | — |
| * — размер для справок. — угол конусов Морзе №0-№5 соответствует углу укороченных конусов Морзе; №6 — 1:19,180 = 0,05214 — угол метрических конусов — 1:20 = 0,05. |
Профиль резьбового отверстия соответствует отверстию центровому форма Р
по
ГОСТ ГОСТ 14034-74
.
В ГОСТ 25557-2006 все размеры центрового отверстия приводятся в общей таблице. Стандарт также определяет размеры пазов канавок и отвестий, необходимых для конструирования конусов, в случае подачи смазочно-охлаждающей жидкости (СОЖ) через инструмент.
В зависимости от конструкции инструментальный хвостовик может иметь соответствующее обозначение:
BI
— внутренний конус с пазом;
BE
— наружный конус с лапкой;
AI
— внутренний конус с отверстием по оси;
АЕ
— наружный конус с резьбовым отверстием по оси;
BIK
— внутренний конус с пазом и отверстием для подачи СОЖ;
ВЕК
— наружный конус с лапкой и отверстием для подачи СОЖ;
AIK
— внутренний конус с отверстием по оси и отверстием для подачи СОЖ;
АЕК
— наружный конус с резьбовым отверстием по оси и отверстием для подачи СОЖ.
КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ ВНУТРЕННИЕ ( ГОСТ 25557-2006 )КОНУСЫ ВНУТРЕННИЕ И НАРУЖНЫЕ КОНУСНОСТЬЮ 7 : 24 ( ГОСТ 15945-82 )
Допуски конусов внутренних и наружных конусностью 7:24
по ГОСТ 19860-93.
КОНУСЫ ИНСТРУМЕНТОВ Предельные отклонения угла конуса и допуски формы конусов ( ГОСТ 2848-75 )
Степень точности инструментальных конусов обозначается допуском угла конуса заданной степени точности по ГОСТ 8908-81 и определяется предельными отклонениями угла конуса и допусками формы поверхности конуса, числовые значения которых указаны ниже.
Примечания: 1. Отклонения угла конуса от номинального размера располагав в «плюс» — для наружных конусов, в «минус» — для внутренних. 2. ГОСТ 2848-75 для наружных конусов предусматривает также степени точности АТ4 и АТ5. Допуски по ГОСТ 2848-75 распространяются на конусы инструментов по ГОСТ 25557-2006 и ГОСТ 9953-82.
Пример обозначения конуса Морзе 3, степени точности АТ8:
Морзе 3 АТ8 ГОСТ 25557-2006
То же метрического конуса 160, степени точности АТ7:
Метр. 160 АТ7 ГОСТ 25557-2006
То же укороченного конуса В18, степени точности АТ6:
Морзе В18 АТ6 ГОСТ 9953-82
Похожие документы:
ГОСТ 2848-75 — Конусы инструментов. Допуски. Методы и средства контроля ГОСТ 7343-72 — Конусы инструментов с конусностью 1:10 и 1:7. Размеры ГОСТ 10079-71 — Развертки конические с коническим хвостовиком под конусы Морзе. Конструкция и размеры ГОСТ 22774-77 — Конусы и трубки шлифовальные. Типы и размеры ГОСТ 25548-82 — Основные нормы взаимозаменяемости. Конусы и конические соединения. Термины и определения
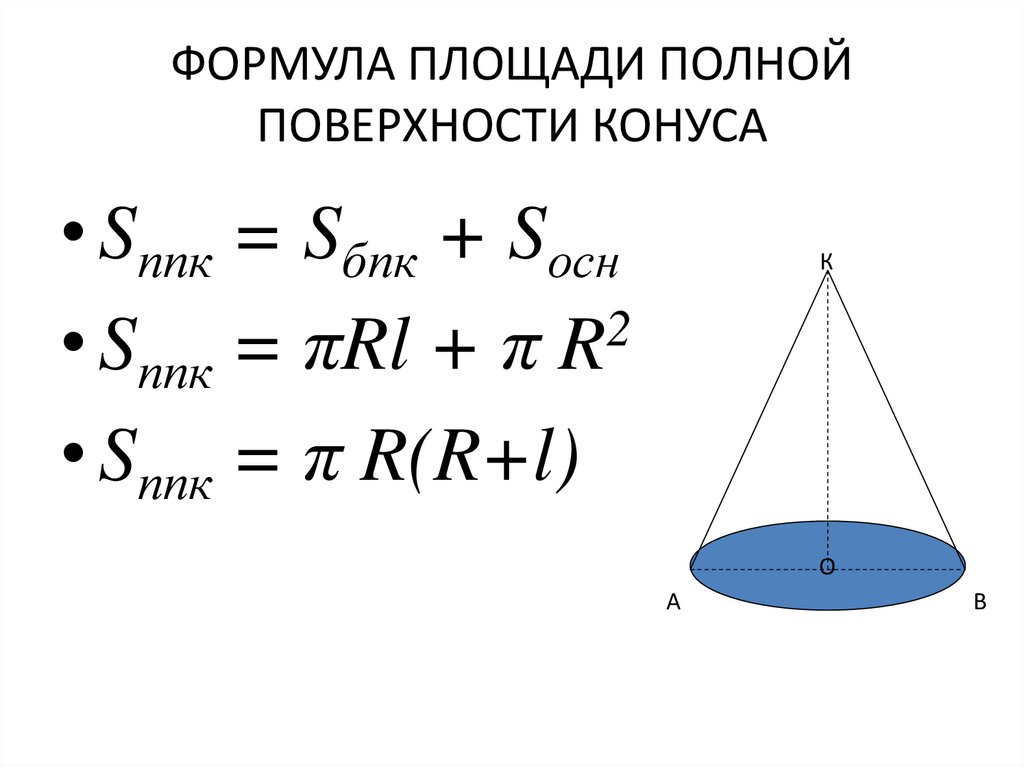
Формула площади конуса
Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:
S = Sбок.пов + Sосн = πRL + πR2
Источники
- https://studwork.org/spravochnik/matematika/obemy-figur/obem-konusa
- https://calcsbox.com/post/formula-obema-konusa.html
- https://worksbase.ru/matematika/formuly/37-konus.html
- https://ru.onlinemschool.com/math/formula/volume/
- https://allcalc.ru/node/36
- https://ru.onlinemschool.com/math/formula/cone/
- https://www.calc.ru/1430.html
- https://MicroExcel.ru/obyom-konusa/
- https://www.calc.ru/obyem-konusa.html
- https://mnogoformul.ru/obem-konusa-formula-i-raschet-onlayn
Площадь усечённого конуса
Для нахождения данного параметра нужно воспользоваться формулами:
- площади боковой поверхности усечённого конуса Sбок;
- полной площади усечённой фигуры Sпол, которая равна сумме площадей двух оснований и площади боковой поверхности:
Здесь l — длина образующей, а R и r — радиусы большего и меньшего оснований соответственно.