Как найти высоту крнуса

Длина отрезка линии опушенной перпендикулярно плоскости основания из вершины конуса является его высотой. Найти не сложно. Для этого нужно знать величину конуса. Если конус велик и внутри его полость, то достаточно опустить из вершины нитку с грузом до основания и измерить длину нитки. Если конус мал и умещается в руках, то достаточно измерить боковую сторону и ширину основания. Половина основания – это один катет. Боковая сторона гипотенуза. А высотой окажется другой катет воображаемого прямоугольного треугольника. К сожалению тут нарисовать не где. Далее, зная значения катета и гипотенузы по теореме Пифагора находим другой катет – высоту конуса. Если конус не симметричный и вершина сдвинута относительно середины, то для расчетов нужно знать угол между плоскостью основания и боковой стороной в месте их измерения. Далее геометрия… Формулы есть в любом справочнике. автор вопроса выбрал этот ответ лучшим Ксарф­акс [156K] 5 лет назад  Высота конуса Это перпендикуляр, который опущен из вершины конуса на основание. Чтобы найти высоту конуса можно воспользоваться несколькими способами. 1) Если известно, чему равен объём конуса, то высоту можно вычислить по формуле: V = 1/3 Sосн * h -> h = 3V / Sосн. При этом для нахождения площади основания (площади круга) нам нужно знать радиус. 2) Образующая конуса, высота и радиус основания образуют прямоугольный треугольник. Поэтому если известна образующая (гипотенуза) и радиус (катет), то высоту можно выразить с помощью теоремы Пифагора. a² = c² – b², a = √(c² – b²). a – высота, b – радиус, c – образующая. Например: Радиус основания = 15 см, длина образующей – 17 см. Высота конуса будет равна √(17² – 15²) = √64 = 8 см. -Irink­a- [281K] 4 года назад  Для того, чтобы найти высоту конуса, необходимо иметь для решения какие-то вводные. Допустим, что мы знаем длина образующей конуса, она равна 10 см. и диаметр его основания равный 12 см. Находим радиус конуса R=D/2= 6 см. Вот наш конус, чертим нужные нам линии. Используем теорему Пифагора, получаем h²=a²-R², где а – длина образующей конуса (10 см), h искомая высота. h² = 100 – 36 = 64 h = √64 = 8 сантиметров Alexg­roovy [14.6K] 5 лет назад  Для поиска высоты конуса нужны входные данные. В качестве таких данных выступает радиус (или диаметр основания) и длина образующей конуса. На рисунке длина образующей обозначена буквой l, а диаметр основания как d. Например, по условию задачи l = 100, d = 56. Решение задачи будет следующим: 88Sky­Walke­r88 [428K] 5 лет назад  Начертим конус, проведем его высоту и основание: Нам известна величина l – это образующая. Она равна 16. Угол между основанием и образующий будет равняться 30 градусам. У нас получился прямоугольный треугольник, в котором образующая (l) – это гипотенуза, а высота (h), которую нам необходимо найти, это катет. Так как нам известен угол, мы можем найти его синус. sin 30° = ½ Известно, что синус – это отношение противолежащего катета к гипотенузе. Следовательно, можно составить такую формулу: sin 30° = h/l = ½ Из этой формулы мы выводим h, высоту конуса. Получается формула и решение: h = sin 30°*l = ½ * 16 = 8. Чосик [208K] более года назад  Зависит от данных, которые мы получили изначально. Для того, чтобы узнать высоту, необходимо знать радиус и апофему. В таком случае мы получим прямоугольный треугольник, где высота и радиус играют роль катетов, а апофема – гипотенузы. Если же мы знает площадь основания и объем конуса, то высота равна h = 3V/S. владс­андро­вич [766K] более года назад  Высоту конуса можно найти разными формулами, тут все зависит от того, что вам известно. В частности если известны площадь его основания и объем самого конуса, то тогда все просто, так как данные значения надо подставить под формулу h = 3V/S и просто посчитать. JuliG­or [3.2K] 9 лет назад  Если известны объем и площадь конуса, то высоту легко найти, так как объем конуса равен одной трети площади основания умноженная на высоту конуса. Также высоту конуса можно найти по теореме Пифагора, но это по-моему гораздо сложнее) morel­juba [62.5K] 5 лет назад  Высоту конуса мы можем выразить из формулы, по которой мы определяем объём конуса: Так вот высота конуса из данной формулы будет равна: Высота конуса = 3 * объём конуса / пи * радиус основания в квадрате. Знаете ответ?

Высота конуса опускается из его вершины ровно в середину основания, являющуюся по совместительству центром окружности, представляющей основание конуса. Для того чтобы найти высоту конуса, необходимо соединить центр окружности с апофемой конуса. Проведенный радиус создаст прямоугольный треугольник внутри конуса, в котором высота и радиус основания будут катетами, а апофема конуса – гипотенузой. Из теоремы Пифагора, высота конуса может быть найдена как квадратный корень из разности квадрата радиуса от квадрата апофемы:

Прочитав данную статью, вы узнаете, как найти высоту конуса. Приведенный в ней материал поможет глубже разобраться в вопросе, а формулы окажутся весьма полезными в решении задач. В тексте разобраны все необходимые базовые понятия и свойства, которые обязательно пригодятся на практике.

Фундаментальная теория

Перед тем, как найти высоту конуса, необходимо разобраться с теорией.

Конус – фигура, которая плавно сужается от плоского основания (часто, хотя и необязательно, кругового) до точки, называемой вершиной.

Конус формируется набором отрезков, лучей или прямых, соединяющих общую точку с основанием. Последнее может ограничиваться не только окружностью, но и эллипсом, параболой или гиперболой.

Ось – это прямая (если таковая имеется), вокруг которой фигура имеет круговую симметрию. Если угол между осью и основой составляет девяносто градусов, то конус принято называть прямым. Именно такая вариация чаще всего встречается в задачах.

Если в основе лежит многоугольник, то объект является пирамидой.

Отрезок, соединяющий вершину и линию, ограничивающую основание, называют образующей.

Как найти высоту конуса

Подойдем к вопросу с другой стороны. Для начала используем объем конуса. Чтобы его найти нужно вычислить произведение высоты с третьей частью площади.

V = 1/3 × S × h.

Очевидно, что из этого можно получить формулу высоты конуса. Достаточно лишь сделать правильные алгебраические преобразования. Разделим обе части равенства на S и умножим на тройку. Получим:

h = 3 × V × 1/S.

Теперь вы знаете, как найти высоту конуса. Однако для решения задач вам могут понадобиться и другие знания.

Важные формулы и свойства

Приведенный ниже материал однозначно поможет вам в решении конкретных задач.

Центр массы тела находится на четвертой части оси, начиная от основы.

В проективной геометрии цилиндр – это просто конус, вершина которого находится на бесконечности.

Следующие свойства работают только для прямого кругового конуса.

• Даны радиус основания r и высота h, тогда формула для площади будет выглядеть так: П × r². Соответственно изменится и окончательное уравнение. V = 1/3 × П × r² × h.
• Вычислить площадь боковой поверхности можно перемножив число “пи”, радиус и длину образующей. S = П × r × l.
• Пересечение произвольной плоскости с фигурой является одним из конических сечений.

Часто встречаются задачи, где необходимо использовать формулу для объема усеченного конуса. Она выводится из обычной и имеет такой вид:

V = 1/3 × П × h × (R² + Rr + r²), где: r -радиус нижнего основания, R – верхнего.

Всего этого будет вполне достаточно для решения разнообразнейших примеров. Разве что могут понадобиться знания, не связанные с этой темой, например, свойства углов, теорема Пифагора и другое.

Геометрия, 11 класс

Урок №7. Конус

Перечень вопросов, рассматриваемых в теме:

• коническая поверхность, образующая конической поверхности, её вершина, ось;
• конус, основание конуса, вершина конуса, образующие конуса, ось конуса, высота конуса;
• боковая поверхность конуса, полная поверхность конуса;
• сечение конуса и его виды;
• усечённый конус и его элементы.
• площади поверхностей усеченного конуса.

Глоссарий по теме

Коническая поверхность – это поверхность, образованная прямыми, проходящими через все точки окружности, и точку, не лежащую в плоскости этой окружности.

Эти прямые – образующие конической поверхности.

Прямая, проходящая через центр окружности, перпендикулярно к плоскости – ось конической поверхности.

Конус– тело, ограниченное конической поверхностью, точкой и кругом.

Круг – основание конуса; точка – вершина конуса, отрезки образующих, заключённые между основанием и вершиной – образующие конуса; образованная ими часть конической поверхности – боковая поверхность конуса.

Ось конической поверхности называется осью цилиндра.

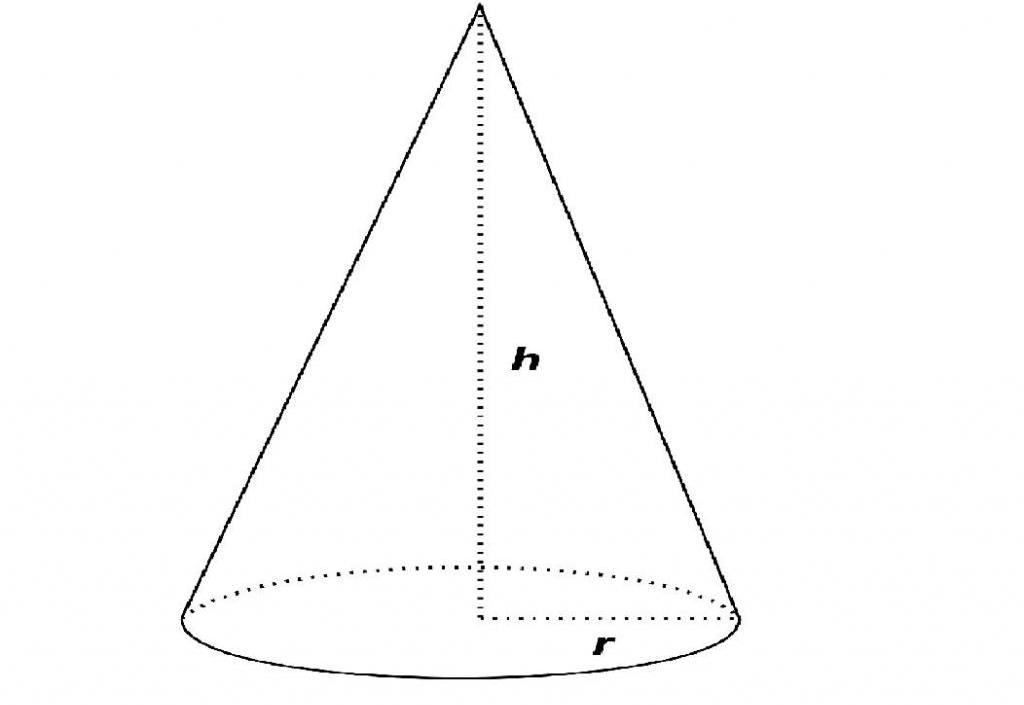
Расстояние от вершины до основания конуса называется высотой конуса, а радиус основания – радиусом конуса.

Сечение – изображение фигуры, образованной рассечением тела плоскостью.

Осевое сечение – вариант сечения, при котором плоскость проходит через ось тела.

Развёртка боковой поверхности конуса – сектор, радиус которого – образующая конуса, а длина дуги – длина окружности основания конуса.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 130-133.

Дополнительная литература:

Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. Учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-79.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

1. Основные определения

В плоскости 𝛂 построю окружность L с центром в точке О. Проведу прямую ОР перпендикулярно плоскости 𝛂. Соединю точку Р со всеми точками окружности L прямыми линиями. Поверхность, состоящую из этих прямых, называют конической поверхностью, сами прямые называют образующими конической поверхности, точку Р называют вершиной, а прямую ОР – осью конической поверхности.

Ввожу новые понятия конуса, основания конуса, вершины конуса, образующих конуса, боковой поверхности конуса, оси конуса и высоты конуса.

Определение

Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом.

Определение

Круг называют основанием конуса.

Определение

Вершину конической поверхности называют вершиной конуса.

Определение

Отрезки образующих, заключённые между вершиной и основанием называют образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса.

Определение

Ось конической поверхности называют и осью конуса, а её отрезок, заключённый между вершиной и основанием называют высотой конуса.

Отмечу, что все образующие конуса равны друг другу. Это легко доказать, если рассмотреть различные прямоугольные треугольники, в которых один катет – это высота конуса, а вторыми катетами являются радиусы основания конуса. Тогда образующие, являясь гипотенузами этих прямоугольных треугольников с равными катетами, также будут равны.

Конус можно получить ещё одним способом – вращением прямоугольного треугольника вокруг одного из катетов. Тогда этот катет (вокруг которого происходит вращение) будет совпадать с осью конуса и будет его высотой, гипотенуза станет образующей и будет образовывать боковую поверхность, а оставшийся катет образует основание, одновременно являясь его радиусом.

2. Сечения конуса различными плоскостями

1. Пусть секущая плоскость проходит через ось конуса. Такое сечение называют осевым. Оно представляет собой равнобедренный треугольник, боковые стороны которого – образующие конуса, а его основанием является диаметр основания конуса.

1. Если секущая плоскость перпендикулярна оси конуса, то сечение представляет собой круг с центром, расположенном на оси.

Это два основных вида сечения конуса, которые изучаются в средней школе на базовом уровне. Следует упомянуть, что существуют и другие сечения конусов, вид которых зависит от расположения секущей плоскости относительно оси.

3. Основные формулы

Формула для вычисления площади боковой поверхности конуса: S_бок=𝛑RL.

Площадь полной поверхности конуса: S_полн=𝛑R(R+L).

4. Усеченный конус

Если взять произвольный конус и провести секущую плоскость перпендикулярно его оси, то исходный конус разделится на две части. Верхняя часть представляет собой конус меньших размеров, а оставшуюся часть называют усечённым конусом.

Определение

Основание исходного конуса и круг, получившийся в сечении, называют основаниями усечённого конуса.

Определение

Отрезок, соединяющий центры оснований, называют высотой усечённого конуса.

Определение

Часть конической поверхности, ограничивающая усечённый конус, называется боковой поверхностью усечённого конуса.

Определение

Отрезки образующих, заключённые между основаниями, называются образующими усечённого конуса. Отмечу, что все образующие усечённого конуса равны друг другу.

Усечённый конус можно получить ещё одним способом – вращением прямоугольной трапеции вокруг той боковой стороны, которая перпендикулярна основанию.

Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью конуса и будет его высотой, другая боковая сторона станет образующей и при вращении будет образовывать боковую поверхность, а основания трапеции станут соответственно радиусами верхнего и нижнего оснований усечённого конуса.

5. Формула для вычисления площадей поверхностей усеченного конуса

S_{бок.пов.ук}=π(r+R)L

S_{.полн.пов.ук}=π(rL+RL+r²+R²)

Примеры и разбор решения заданий тренировочного модуля

1. Найти высоту конуса, если площадь его осевого сечения равна 6, а площадь основания равна 8.

Решение:

Сделаем чертеж:

S_ABC=6.

Его высота SO является высотой конуса.

S_ABC=SO·OB.

OB – радиус основания.

Его найдем из равенства: S_осн=πR².

8= πR².

R===OB.

Теперь найдем высоту:

6=SO·OB=SO·.

Отсюда: SO=3

Ответ: 3.

2. Прямоугольная трапеция с основаниями 4 и 7 и меньшей боковой стороной 4 вращается вокруг меньшей стороны. Найдите элементы усеченного конуса.

Величина

Высота конуса

Образующая конуса

Радиус меньшего основания

Радиус большего основания

Площадь боковой поверхности конуса

Площадь осевого сечения

Площадь полной поверхности конуса

Решение:

Сделаем чертеж:

Трапеция ABCD вращается вокруг стороны AD.

Тогда:

AD – высота усеченного конуса, AD=4.

АВ – радиус меньшего основания, AB=4.

DC – радиус большего основания, DC=7.

Площадь боковой поверхности конуса вычислим по формуле: S_{бок.пов.ук}=π(r+R)L.

Для того чтобы найти площадь боковой поверхности, нужно найти образующую.

Ее найдем из треугольника BHC: BC=5 (это египетский треугольник).

Теперь найдем площадь боковой поверхности.

S_б.п. =π(4+7)·5=55π.

Площадь боковой поверхности равна 55π.

Осевое сечение представляет собой равнобедренную трапецию с основаниями 8 и 14 и высотой, равной 4.

Так что площадь этой трапеции равна: S=4(4+7)=44.

Для того чтобы найти площадь полной поверхности, нужно к площади боковой поверхности прибавить площади ее оснований.

S_п.п.=55π+16π+49π=120π.

Величина	Значение
Высота конуса	4
Образующая конуса	5
Радиус меньшего основания	4
Радиус большего основания	7
Площадь боковой поверхности конуса	55π
Площадь осевого сечения	44
Площадь полной поверхности конуса	120π

Как найти высоту конуса?

КИИ

Ученик

(192),
закрыт

9 лет назад