Как найти высоту куба вписанного в шар - Сайт, где вы сможете решить свои вопросы

Содержание

В полушар радиусом (корень из 3 / 2) вписан куб таким образом, что четыре его вершины лежат в большом круге шара, а остальные четыре вершины лежат на поверхности шара?
Куб вписан в шар радиуса корень из 3?
Шар радиуса 4см вписан в куб вычислить объем шара и объем куба?
Куб вписан в шар радиуса корень из 3?
Куб с ребром, равным корень из 2 см, вписан в шар?
В куб вписан шар?
Куб вписан в шар радиуса корень из 3 ?
В куб вписан шар радиус 3?
Куб вписан в шар радиусом 3?
Куб вписан в шар (вершины куба лежат на поверхности шара)?
Куб вписан в шар?
Куб вписанный в полушар
Куб вписанный в полушар
Как написать хороший ответ?
Куб вписанный в полушар

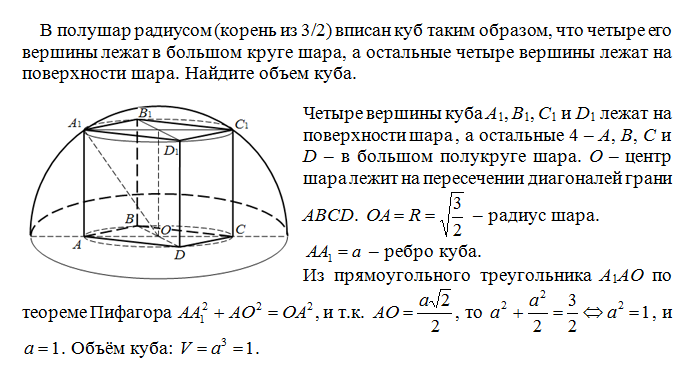
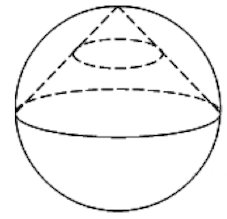
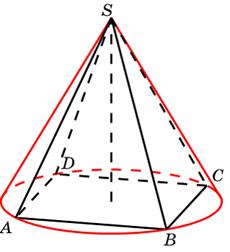
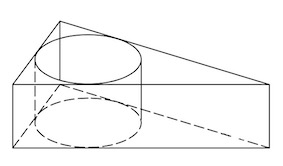
В полушар радиусом (корень из 3 / 2) вписан куб таким образом, что четыре его вершины лежат в большом круге шара, а остальные четыре вершины лежат на поверхности шара?

В полушар радиусом (корень из 3 / 2) вписан куб таким образом, что четыре его вершины лежат в большом круге шара, а остальные четыре вершины лежат на поверхности шара.

Решение во вложенном файле.

Куб вписан в шар радиуса корень из 3?

Куб вписан в шар радиуса корень из 3.

Шар радиуса 4см вписан в куб вычислить объем шара и объем куба?

Шар радиуса 4см вписан в куб вычислить объем шара и объем куба.

Куб вписан в шар радиуса корень из 3?

Куб вписан в шар радиуса корень из 3.

Найдите площадь поверхности куба.

Куб с ребром, равным корень из 2 см, вписан в шар?

Куб с ребром, равным корень из 2 см, вписан в шар.

В куб вписан шар?

Найдите объем шара, если объем куба равен 30.

Куб вписан в шар радиуса корень из 3 ?

Куб вписан в шар радиуса корень из 3 .

Найдите площадь поверхности куба.

В куб вписан шар радиус 3?

В куб вписан шар радиус 3.

Куб вписан в шар радиусом 3?

Куб вписан в шар радиусом 3.

Куб вписан в шар (вершины куба лежат на поверхности шара)?

Куб вписан в шар (вершины куба лежат на поверхности шара).

Поверхность куба равна 18.

Куб вписан в шар?

Найдите радиус шара, если ребро куба равно 10 корень из 3.

На этой странице вы найдете ответ на вопрос В полушар радиусом (корень из 3 / 2) вписан куб таким образом, что четыре его вершины лежат в большом круге шара, а остальные четыре вершины лежат на поверхности шара?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

А) просто чертишь 1 прямую линию и обозначаешь 4 любых точки(например а, б, с) б)чертишь также прямую и обозначашь 5 любых точки(например а, б, с, д) в)и опять же чертишь прямую линию и обозначашь 6 любых точек(например а, б, с, д, е).

Вписанный угол равен половине градусной меры дуги, на которую он опирается)).

PA = x PB = x + AB = x + 6 x + x + 6 = 9 2x = 3 x = 1. 5 PA = 1. 5 PB = 1. 5 + 6 = 7. 5.

2 угла = 151градус( т. К. вертикальные) Другие 2 угла = 180 — 151 = 29 градусов ( т. К. углы смежные с первыми углами).

Пусть меньшая сторона равна х см, тогда большая сторона параллелограмма равна х + 4 см . По условию (х + 4) / х = 4 / 3, 3х + 4·3 = 4х, х = 12. Одна сторона параллелограмма равна 12 см, другая 12 + 4 = 16 см. Ответ 12 см, 16 см.

1. Через середины сторон треугольника проходят средние линии. Длина средней линии в два раза меньше, чем длина параллельной ей стороны. Т. е. Длины средних линий будут 4, 2. 5, 3. 5см, а периметр p = 4 + 2. 5 + 3. 5 = 10 см. 2. прямая, опущен..

Рисуем стороны, углы. Отнимаем, получаем 77 градусов.

Ответ : Угол между векторами равен arccos(0, 316) ≈ 71, 58°. Объяснение : Угол α между векторами a и b вычисляется по формуле : cosα = (Xa * Xb + Ya * Yb) / [√(Xa² + Ya²) * √(Xb² + Yb²)]. В нашем случае : скалярное произведение Xa * Xb + Ya * Yb = ..

Источник

Куб вписанный в полушар

Переложите пирамиду из 10 кубиков (см. рисунок) так, чтобы её форма осталась прежней, но каждый кубик соприкасался только с новыми кубиками.

В музее Гугенхайм в Нью-Йорке есть скульптура, имеющая форму куба. Жук, севший на одну из вершин, хочет как можно быстрее осмотреть скульптуру, чтобы перейти к другим экспонатам (для этого достаточно попасть в противоположную вершину куба). Какой путь ему выбрать?

Можно ли расставить на ребрах куба числа от 1 до 12 так, чтобы все суммы чисел на гранях были одинаковыми?

На прозрачном столе стоит куб 3×3×3, составленный из 27 одинаковых кубиков. Со всех шести сторон (спереди, сзади, слева, справа, сверху, снизу) мы видим квадрат 3×3. Какое наибольшее число кубиков можно убрать так, чтобы со всех сторон был виден квадрат 3×3 и при этом оставшаяся система кубиков не разваливалась?

На гранях кубика расставлены числа от 1 до 6. Кубик бросили два раза. В первый раз сумма чисел на четырёх боковых гранях оказалась равна 12, во второй — 15. Какое число написано на грани, противоположной той, где написана цифра 3?

Страница: 1 2 3 4 5 6 7 >> [Всего задач: 204]

Проект осуществляется при поддержке и .

Источник

Куб вписанный в полушар

В полушар радиусом (корень из 3/2) вписан куб таким образом, что четыре его вершины лежат в большом круге шара, а остальные четыре вершины лежат на поверхности шара. Найдите объем куба.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Решение во вложенном файле.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Источник

Куб вписанный в полушар

В куб с ребром 21 вписан шар. Найдите объем этого шара, деленный на

Радиус вписанного в куб шара равен половине длины ребра куба: Тогда объем шара

Аналоги к заданию № 27126: 75315 75317 75319 Все

В прямоугольный параллелепипед вписана сфера с радиусом 4. Найдите объём параллелепипеда.

Поскольку сфера вписана в прямоугольный параллелепипед, прямоугольный параллелепипед — это куб, ребро которого равно двум радиусам вписанной сферы. Объём куба равен кубу его ребра. Следовательно,

В прямоугольный параллелепипед вписана сфера с радиусом 5. Найдите объём параллелепипеда.

Аналоги к заданию № 525402: 525447 Все

Шар, объём которого равен 6π, вписан в куб. Найдите объём куба.

Ребро куба равно двум радиусам вписанного в куб шара, поэтому объем куба, выраженный через радиус вписанного в него шара, даётся формулой Объём шара вычисляется по формуле откуда имеем:

Тем самым, объём куба равен 36.

Шар, объём которого равен вписан в куб. Найдите объём куба.

Тем самым, объём куба равен 210.

Шар, объём которого равен 28π, вписан в куб. Найдите объём куба.

Тем самым, объём куба равен 168.

Шар, объём которого равен 44π, вписан в куб. Найдите объём куба.

Тем самым, объём куба равен 264.

Известно, что AB, AC, AD, DE, DF — рёбра куба. Через вершины E, F и середины рёбер AB и AC проведена плоскость P, делящая шар, вписанный в куб, на две части.

б) Найдите отношение объёма меньшей части шара к объёму всего шара.

а) Проведем TK, KF и ET и получим искомое сечение — равнобедренную трапецию FKTE.

б) Введем обозначения, как показано на рисунке. Пусть точка O — середина высоты куба и центр вписанного шара, точки O₁ и O₂ — центры нижней и верхней граней куба соответсвенно, а также точки касания шара с гранями. Пусть R — радиус шара. Очевидно, что сечением шара плоскостью P является круг, центр которого лежит на NO₂, где N — середина TK. Более того, центром данного круга является точка H — основание перпендикуляра из O на NO₂, а радиусом — HO₂. Наша задача сводится к нахождению объема шарового сегмента. Основание шарового сегмента есть круг с центром H и радиусом HO₂, высотой сегмента является отрезок, равный Найдем значения этих элементов.

Тогда по формуле объема шарового сегмента находим

Следовательно, отношение объемов равно

Ответ:

Источник: А. Ларин: Тренировочный вариант № 87.

Источник

Adblock
detector

Источник

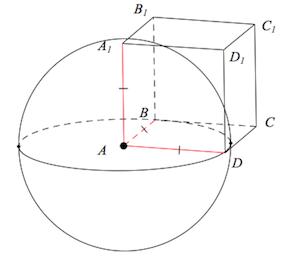
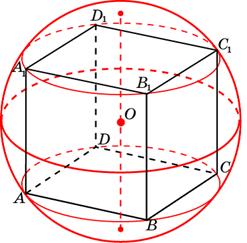
Шар является описанным около куба, если все вершины куба находятся на поверхности шара.

Центр шара (O) — точка пересечения диагоналей куба.

Около любого куба можно описать шар.

Общие точки шара и куба — восемь вершин куба.

Чертится диагональное сечение.

AC1

CA1

— диагонали куба.

Радиус шара равен половине диагонали куба.

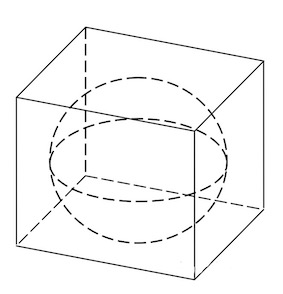
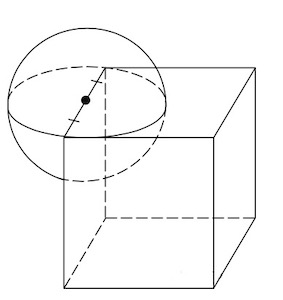
Шар является вписанным в куб, если он касается всех его граней.

Центр шара (O) находится в точке пересечения диагоналей куба.
В любой куб можно вписать шар.
Общие точки шара и куба — центры шести граней куба (точки касания шара и куба).

Чертится сечение плоскостью, которая параллельна грани куба и проходит через центр шара.

Радиус шара — половина стороны куба.

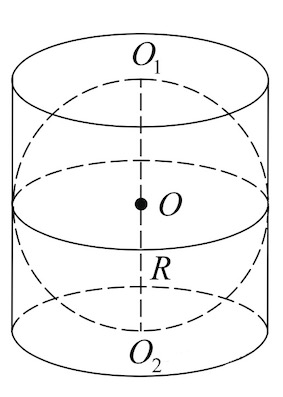
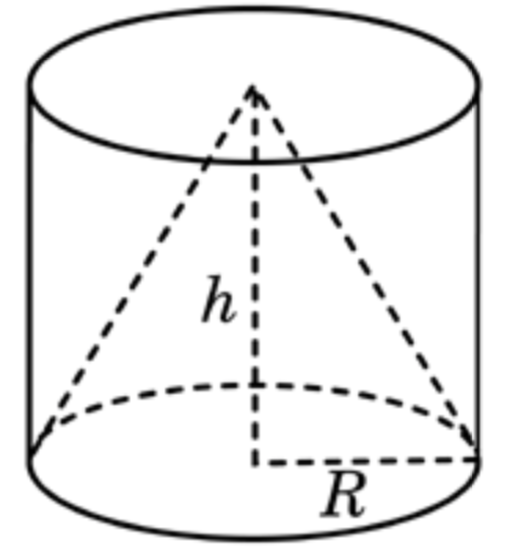
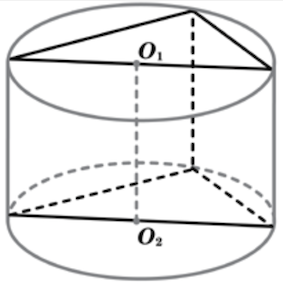
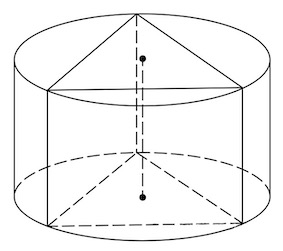
Шар является описанным около цилиндра, если окружности оснований цилиндра лежат на поверхности шара.

Центр шара (O) находится в середине высоты цилиндра.

Общие элементы — две окружности.

Около любого цилиндра можно описать шар.

Чертится осевое сечение.

Радиус шара — половина диагонали осевого сечения цилиндра.

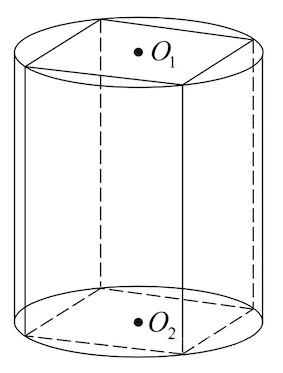
Шар является вписанным в цилиндр, если касается оснований цилиндра и всех его образующих.

Центр шара (O) — середина высоты цилиндра.

Осевое сечение — квадрат с вписанной в него окружностью.

Радиус шара равен радиусу цилиндра и половине высоты цилиндра.

Источник

В данной публикации мы рассмотрим, как можно найти радиус вписанного в куб шара (сферы), если известна длина ребра куба или его диагональ.

Примечание: Напомним, что в любой куб можно вписать шар.

Для начала выполним чертеж.

шар касается всех 6 граней куба (на рисунке показаны только 4 точки касания);
центр шара – точка O, которая также является центром куба.

Радиус шара (R), вписанного в куб, равняется половине его ребра, т.е.:

R = a/2, где “a” – ребро куба (является стороной его грани).

Чтобы было понятнее, выполним сечение, параллельное одной из граней куба и проходящее через точки касания шара двух других параллельных друг другу граней. Это сечение, в том числе, проходит через середины соответствующих сторон.

Таким образом, мы получим квадрат со вписанной окружностью, радиус которой равняется половине его стороны, которая в свою очередь равна ребру куба.

Радиус вписанного шара через диагональ куба

Если известна длина диагонали куба (примем ее за “d”), радиус вписанного в него шара (R) можно вычислить так:

Источник

Светило науки – 7292 ответа – 165986 раз оказано помощи

Диаметр вписанного в куб шара равен длине ребра куба, а радиус – половине длины ребра.

Площадь полной поверхности куба равна сумме площадей его 6-ти граней.

Площадь одной грани равна а² =1170/π :6=195/π

R²= (a/2)²=195/4π

Из формулы площади поверхности шара

S=4πR²=4π•195/4π=195 (ед. площади)

Окружности, ограничивающие основания вписанного цилиндра изнутри касаются шара.

Осевое сечение цилиндра – прямоугольник, проходит через центр шара, при этом диаметр шара является диагональю этого прямоугольника.

Из формулы площади поверхности сферы 4πR²=100π находим её радиус R=5 ⇒ D=10

Диаметр основания цилиндра d=2r=8.

Из прямоугольного ∆ АВС высота ( образующая) цилинда ВС=6 ( по т.Пифагора или обратив внимание на отношение катета АС и гипотенузы АВ 4:5 – отношение сторон “египетского” треугольника)

Высота цилиндра – 6 ед. длины.

Источник

Задача 1. Объем прямоугольного параллелепипеда, описанного около сферы, равен Найдите радиус сферы.

Решение: + показать

Задача 2. В куб вписан шар радиуса Найдите объем куба.

Решение: + показать

Задача 3. Шар, объём которого равен вписан в куб. Найдите объём куба.

Решение: + показать

Задача 4. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен Объем параллелепипеда равен Найдите высоту цилиндра.

Решение: + показать

Задача 5. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны Найдите объем параллелепипеда.

Решение: + показать

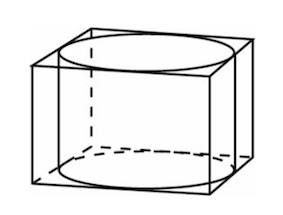
Задача 6. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны Найдите площадь боковой поверхности призмы.

Решение: + показать

Задача 7. В основании прямой призмы лежит квадрат со стороной . Боковые ребра равны $frac{5}{pi}.$ Найдите объем цилиндра, описанного около этой призмы.

Решение: + показать

Задача 8. Около шара описан цилиндр, площадь поверхности которого равна Найдите площадь поверхности шара.

Решение: + показать

Задача 9. Цилиндр описан около шара. Объем цилиндра равен Найдите объем шара.

Решение: + показать

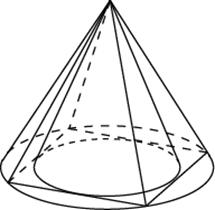
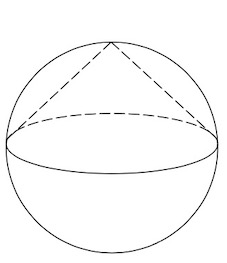
Задача 10. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен Найдите объем конуса.

Решение: + показать

Задача 11. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен Найдите объем шара.

Решение: + показать

Задача 12. Середина ребра куба со стороной является центром шара радиуса Найдите площадь части поверхности шара, лежащей внутри куба. В ответе запишите $frac{S}{pi}.$

Решение: + показать

Задача 13. Вершина куба со стороной является центром сферы, проходящей через точку . Найдите площадь части сферы, содержащейся внутри куба. В ответе запишите величину $frac{S}{pi}$ .

Решение: + показать

Задача 14. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен

Решение: + показать

Задача 15. Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса.

Решение: + показать

Задача 16. Конус описан около правильной четырехугольной пирамиды со стороной основания и высотой Найдите его объем, деленный на .

Решение: + показать

Задача 17. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Решение: + показать

Задача 18. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен Найдите объем конуса.

Решение: + показать

Задача 19. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен Найдите образующую конуса.

Решение: + показать

Задача 20. В основании прямой призмы лежит прямоугольный треугольник с катетами и Боковые ребра равны $frac{6}{pi}$ . Найдите объем цилиндра, описанного около этой призмы.

Решение: + показать

Задача 21. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна

Решение: + показать

Задача 22. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен а высота равна

Решение: + показать

Задача 23. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен

Решение: + показать

Задача 24. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна

Решение: + показать

Задача 25. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна