В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
-
Нахождение высоты треугольника
- Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
-
Высота в прямоугольном треугольнике
- Высота в равностороннем треугольнике
- Примеры задач
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Как найти в треугольнике высоту?
Анонимный вопрос
25 января 2018 · 91,7 K
Мне интересны множество тем: от психологии до космоса…) · 14 нояб 2018
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (для тупого угла – на продолжение стороны треугольника).
В зависимости от входных данных, высоту треугольника можно найти разными способами.
- Если известны длины всех сторон
h = 2/a √p(p-a)(p-b)(p-c),
где h – длина высоты треугольника, p – полупериметр, a – длина стороны, на которую падает высота (основание), b и c – длины двух других сторон треугольника.
- Если известна длина одной из сторон треугольника и угол между этой стороной и основанием треугольника
h = b ∙ sinγ = c ∙ sinβ
- Если известна длина основания и площадь треугольника
h = 2S/a
- Если известны длины двух сторон треугольника и радиус описанной вокруг треугольника окружности
h = 2S/a
51,9 K
1 это для нахождения площади
Комментировать ответ…Комментировать…
Высота треугольника это перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону, или на ее продолжение (сторона, на которую опускается перпендикуляр, в данном случае называется основанием треугольника). Все формулы для расчета высоты треугольника можно посмотреть на http://www-formula.ru/heighttriangle
14,7 K
Комментировать ответ…Комментировать…
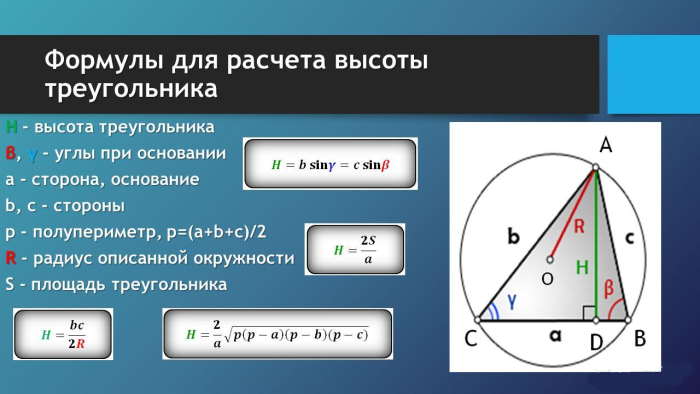
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

a – сторона, основание
b, c – стороны
β, γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
- Подробности
-
Опубликовано: 09 октября 2011
-
Обновлено: 13 августа 2021
Download Article
Download Article
To calculate the area of a triangle you need to know its height. To find the height follow these instructions. You must at least have a base to find the height.
-
1
Recall the formula for the area of a triangle. The formula for the area of a triangle is
A=1/2bh.
[1]
- A = Area of the triangle
- b = Length of the base of the triangle
- h = Height of the base of the triangle
-
2
Look at your triangle and determine which variables you know. You already know the area, so assign that value to A. You should also know the value of one side length; assign that value to “‘b'”.
Any side of a triangle can be the base,
regardless of how the triangle is drawn. To visualize this, just imagine rotating the triangle until the known side length is at the bottom.
Example
If you know that the area of a triangle is 20, and one side is 4, then:
A = 20 and b = 4.Advertisement
-
3
Plug your values into the equation A=1/2bh and do the math. First multiply the base (b) by 1/2, then divide the area (A) by the product. The resulting value will be the height of your triangle!
Example
20 = 1/2(4)h Plug the numbers into the equation.
20 = 2h Multiply 4 by 1/2.
10 = h Divide by 2 to find the value for height.
Advertisement
-
1
Recall the properties of an equilateral triangle. An equilateral triangle has three equal sides, and three equal angles that are each 60 degrees. If you
cut an equilateral triangle in half, you will end up with two congruent right triangles.
[2]
- In this example, we will be using an equilateral triangle with side lengths of 8.
-
2
Recall the Pythagorean Theorem. The Pythagorean Theorem states that for any right triangle with sides of length a and b, and hypotenuse of length c:
a2 + b2 = c2.
We can use this theorem to find the height of our equilateral triangle![3]
-
3
Break the equilateral triangle in half, and assign values to variables a, b, and c. The hypotenuse c will be equal to the original side length. Side a will be equal to 1/2 the side length, and side b is the height of the triangle that we need to solve.
- Using our example equilateral triangle with sides of 8, c = 8 and a = 4.
-
4
Plug the values into the Pythagorean Theorem and solve for b2.[4]
First square c and a by multiplying each number by itself. Then subtract a2 from c2.Example
42 + b2 = 82 Plug in the values for a and c.
16 + b2 = 64 Square a and c.
b2 = 48 Subtract a2 from c2. -
5
Find the square root of b2 to get the height of your triangle! Use the square root function on your calculator to find Sqrt(2. The answer is the height of your equilateral triangle!
- b = Sqrt (48) = 6.93
Advertisement
-
1
Determine what variables you know. The height of a triangle can be found if you have 2 sides and the angle in between them, or all three sides. We’ll call the sides of the triangle a, b, and c, and the angles, A, B, and C.
- If you have all three sides, you’ll use
Heron’s formula
, and the formula for the area of a triangle.
- If you have two sides and an angle, you’ll use the formula for the area given two angles and a side.
A = 1/2ab(sin C).[5]
- If you have all three sides, you’ll use
-
2
Use Heron’s formula if you have all three sides. Heron’s formula has two parts. First, you must find the variable
s, which is equal to half of the perimeter of the triangle.
This is done with this formula:
s = (a+b+c)/2.[6]
Heron’s Formula Example
For a triangle with sides a = 4, b = 3, and c = 5:
s = (4+3+5)/2
s = (12)/2
s = 6
Then use the second part of Heron’s formula, Area = sqr(s(s-a)(s-b)(s-c). Replace Area in the equation with its equivalent in the area formula: 1/2bh (or 1/2ah or 1/2ch).
Solve for h. For our example triangle this looks like:
1/2(3)h = sqr(6(6-4)(6-3)(6-5).
3/2h = sqr(6(2)(3)(1)
3/2h = sqr(36)
Use a calculator to calculate the square root, which in this case makes it 3/2h = 6.
Therefore, height is equal to 4, using side b as the base. -
3
Use the area given two sides and an angle formula if you have a side and an angle. Replace area in the formula with its equivalent in the area of a triangle formula: 1/2bh. This gives you a formula that looks like 1/2bh = 1/2ab(sin C). This can be simplified to
h = a(sin C)
, thereby eliminating one of the side variables.[7]
Note that angle C and side a are both positioned across from the height that you need to find (both on the right side from it, or both on the left side).Finding Height with 1 Side and 1 Angle Example
For example, with a = 3, and C = 40 degrees, the equation looks like this:
h = 3(sin 40)
Use your calculator to finish the equation, which makes h roughly 1.928.
Advertisement
Practice Problems and Answers
Add New Question
-
Question
How do I find the area of an equilateral triangle when only the height is given?
H = height, S = side, A = area, B = base. You know that each angle is 60 degrees because it is an equilateral triangle. If you look at one of the triangle halves, H/S = sin 60 degrees because S is the longest side (the hypotenuse) and H is across from the 60 degree angle, so now you can find S. The base of the triangle is S because all the sides are the same, so B = S. Using A = (1/2)*BH, you get A = (1/2)*SH, which you can now find.
-
Question
How do I calculate the height of a right triangle, given only the length of the base and the interior angle at the base?
Look up the tangent of the angle in a trigonometry table. Multiply the tangent by the length of the base.
-
Question
How do I determine the height of a triangle when I know the length of all three sides?
You already know the base, so calculate the area by Heron’s formula. Then, substitute the values you know in the formula. Area=1/2 * base * height or height=2 * Area/base and find your answer.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
References
About This Article
Article SummaryX
If you know the base and area of the triangle, you can divide the base by 2, then divide that by the area to find the height. To find the height of an equilateral triangle, use the Pythagorean Theorem, a^2 + b^2 = c^2. Cut the triangle in half down the middle, so that c is equal to the original side length, a equals half of the original side length, and b is the height. Plug a and c into the equation, squaring both of them. Then subtract a^2 from c^2 and take the square root of the difference to find the height. If you want to learn how to calculate the area if you only know the angles and sides, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 2,397,778 times.
Reader Success Stories
-
“My Geometry teacher is not the best teacher, and I usually have to look up terms and lessons so I can teach myself…” more
Did this article help you?
Определение высоты треугольника
Перед тем как изучать формулы рассмотрим само определение. Это базовая информация, которая позволяет понять значение и предназначение такого показателя.
Высота треугольника – перпендикуляр, который проводится от вершины фигуры к прямой, имеющей противоположную сторону.
Критерии, зависящие от типа треугольника:
-
Внутри геометрической фигуры (подходит для остроугольных).
-
Совпадает с его стороной (подходит для прямоугольных).
-
Проходит вне фигуры (подходит для тупоугольных).
Как найти высоту треугольника
Можно воспользоваться одной из предложенных формул. Наиболее подходящая выбирается, исходя из известных значений. Это поможет не запутаться на середине решения и не пересчитывать по каждой формуле числа, делая из них уравнения. Существует множество выражений, способных в этом помочь. Ниже приведены самые распространенные и простые варианты определения этого показателя.
Через площадь треугольника
Этот способ можно использовать для всех видов фигуры. Чтобы воспользоваться формулой, должны быть известны площадь фигуры со стороной с проведенной высотой. В любой форме перпендикуляры не будут равны, поэтому вычислять возможно лишь одну высоту для одной стороны.
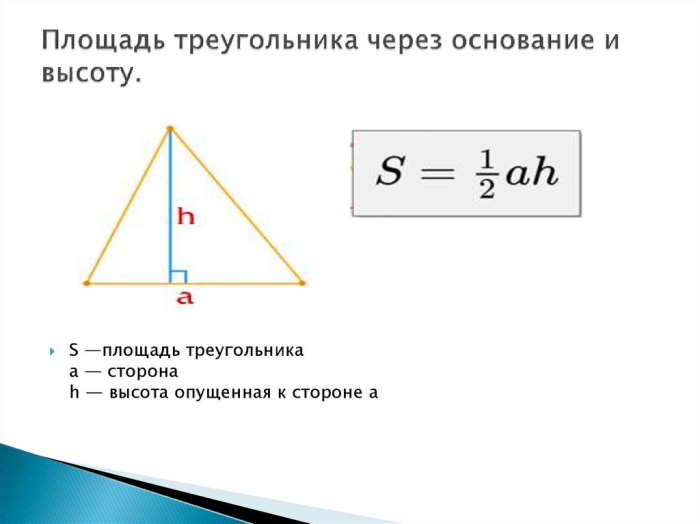
Формула площади треугольника:
S=½∗bh, где b – сторона фигуры, h – проведенная к стороне высота
Таким образом можно выразить перпендикуляр. С этой целью существует следующее выражение:
h=2∗S/b
Пример 1. Чему равна высота равностороннего треугольника АВС, если его площадь составляет 24 см, а длина стороны А составляет одну треть от площади.
Решение:
А=24/3=8 см
h=2∗S/b=2*24/8=6 см
Через теорему Пифагора
Для данного способа хорошо подойдут равнобедренные или равносторонние формы. В случае нахождения высоты равнобедренного треугольника следует знать, где находится основание. Это поможет в определении его боковых сторон, которые в данной форме уравненные и определении высоты, имеющей некоторые свойства:
-
совпадение высоты с биссектрисой и медианой;
-
деление основания пополам.
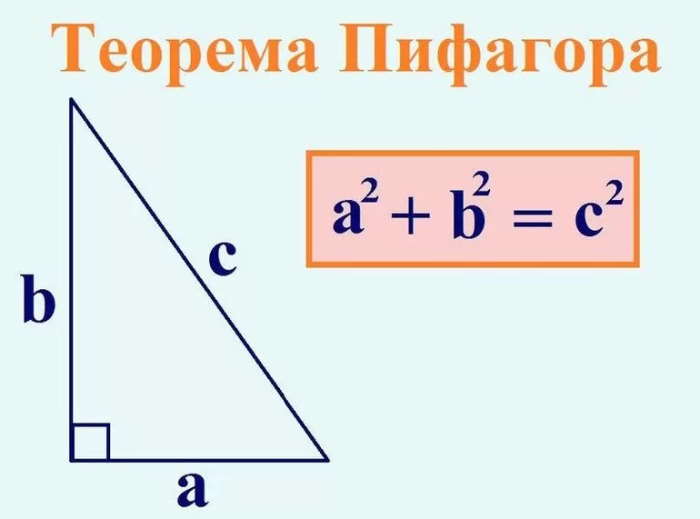
Формула определения высоты треугольника через теорему Пифагора:
BD=√(BC2−HC2)
Пример 2. Длина катетов прямоугольного треугольника равна 7 см. Вычислите длину его гипотенузы.
Исходя из теоремы Пифагора, длина гипотенузы прямоугольной формы, возведенной в квадрат, равна сумме, полученной в результате сложения квадратов длин его катетов:
х² = 7^2+7^2
Извлекаем квадрат из обеих частей равенства:
x = √(7² + 7²)= √(49+49) = √98 = √49*2 = 7√2=9,89 см
Через тригонометрическую функцию
Такой способ может помочь в решении задачи, если известны как сторона, так и угол при основании. В этом может помочь тригонометрическая функция.
Формула выражения высоты фигуры через тригонометрическую функцию:
BH=BC∗cos(60°)
Пример 3. Дан треугольник АВС. Угол C равен 90°, АС=2,4, sinA=7/25 Найдите AB.
Зная, что sinA=7/25, можно найти cosA. Для этого воспользуемся следующими формулами:
cosA = √1- sin2A = √1 -49/625=24/25
AB = AC/cosA = 4,8:24/25 = 4,8*25/24 = 48/10*25/24 = 5.