Как найти высоту между двумя горизонталями

Задачи

Определяют отметку
точки Р,
лежащей между горизонталями. Высоту
точки, расположенной между горизонталями,
определяют линейной интерполяцией по
высотам соседних с ней горизонталей.

Высоты двух соседних
горизонталей равны большей 77,00 и меньшей
78,00; высоту сечения рельефа обозначим
h_сеч.
Через точку Р
проводим
прямую, примерно перпендикулярно этим
горизонталям. На плане измеряем отрезки.
Высоту точки Р
находят из выражения:

=>
, (18)

H_p
=H_г
+
h₀, (19)

d₀
= 5мм

d
= 13мм.

высота сечения
рельефа h_сеч
= 1метр

h₀
= 1 * 5 / 13 = 0,38

Н_p
= 78 + 0,38 = 78,38м.

6.2 Построение профиля по заданному направлению

Строят профиль
АВ. В отведенном для построения профиля
месте плана проводят линию условного
горизонта, на которой в масштабе плана
наносят расстояния между точками, это
пересечение лини АВ с горизонталями.
Для быстроты выполнения к линии АВ
прикладывают полоску бумаги, на которой
отмечают расстояния между горизонталями
по линии АВ. Затем их, перенося на линию
условного горизонта. Высоту линии
условного горизонта принимают так,
чтобы самые низкие точки профиля
находились выше этой линии на 1-2см. К
нанесённым точкам на линии условного
горизонта восстанавливают перпендикуляры,
на которых откладывают высоты точек в
масштабе 1:100. Соединяют между собой
отложенные по перпендикулярам точки,
получают профиль по заданному направлению.
Ниже линии условного горизонта строят
графы профиля (высоты точек, горизонтальные
расстояния). Эти графы заполняют данными,
полученными непосредственно с плана.

1:2000

в
1см 20м

Масштаб
горизонтального 1:2000

вертикального 1:100

0,75 
20= 15

0,70 
20= 14

1

В

А

,03 
20= 20,6

1,12 
20= 22,4

6.3 Построение график уклонов.

Расчеты для
построения графика заложений выполняют
исходя из заданных уклонов через 0,01 и
высоты сечения рельефа h
= 1 м по формуле:

, (20)

где d
– величина заложения,

i
– задаваемый уклон.

Весь расчёт удобно
выполнить в таблице1:

Таблица 1

i	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09	0,10
d, м	100	50	33	25	20	16	14	12	11	10
d, см	5	2,5	1,7	1,3	1	0,9	0,7	0,6	0,6	0,5

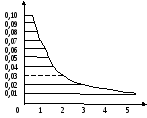
Рисунок 10 – График
уклонов

По вычисленным
значениям заложений (соответствующим
заданным уклоном) строят график. Для
этого проводят две взаимно перпендикулярные
линии (горизонталь и вертикально) и на
одной из них откладывают одинаковые
отрезки (примерно через 0,5 см), на концах
которых последовательно (снизу вверх)
подписывают уклоны, а по другой откладывают
отрезки, соответствующие значениям
заложений. Концы отрезков соединяют
плавной кривой (рис.10).

После чего
проектируют нужный уклон на плане
(например, 0,03), соединяя две соседние
горизонтали высот.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Определение отметок точек и превышений

Системы вертикальных (высотных) координат

Основной величиной в этой системе является высота. Высотой точки называется расстояние по отвесной линии от уровенной поверхности до данной точки. Числовое значение высоты точки является ее отметкой.

Если высоты отсчитываются от основной уровенной поверхности, то они называются абсолютными и входят в абсолютную систему высот. Если же высоты отсчитываются от любой другой уровенной поверхности, условно принятой за начальную, то они называются условными и входят в условную систему высот.

В России и сопредельных государствах положение основной уровенной поверхности, совпадающей со средним многолетним уровнем Балтийского моря, фиксируется нулевым горизонтальным штрихом на бронзовой доске, прикрепленной к устою моста через обводной канал в Кронштадте. Эта доска с нулевым штрихом, от которого ведется отсчет абсолютных высот, называется Кронштадским футштоком.

Высота одной точки (В) относительно другой (А) называется относительной высотой или превышением (h). Из рисунка видно, что превышение равно разности абсолютных или условных высот двух точек:

Рис. Абсолютные (HA и HB), условные H’A и H’B и относительные (h) высоты Рельеф земной поверхности и его изображение

На топографических картах

Рельеф – это совокупность всех неровностей земной поверхности, различных по своей форме и размерам. Изображение рельефа на топокартах должно быть наглядным, отражать количественные характеристики неровностей местности (абсолютные высоты, превышения точек, крутизну склонов и др.). Рельеф на топокартах изображается горизонталями в сочетании с отметками высот и условными обозначениями форм, которые нельзя изобразить горизонталями. Способ изображения рельефа горизонталями позволяет геометрически наиболее точно передать форму рельефа и отразить его особенности.

Горизонтали– это кривые линии, соединяющие на карте точки с одинаковыми высотами. Горизонтали представляют проекции сечения местности уровенными поверхностями через определенные высоты.

При изображении рельефа местности горизонталями обязательным является условие, чтобы уровенные поверхности, рассекающие земную поверхность, отстояли одна от другой на одно и то же расстояние h, называемое высотой сечения рельефа. Горизонтали проектируются на горизонтальную плоскость М (или на поверхность эллипсоида) для изображения их на плане (или карте). Для того чтобы отличить изображения положительных (гор) и отрицательных (котловин) форм рельефа, от одной или нескольких горизонталей проводятся скатштрихи (бергштрихи) в сторону понижения ската (рис. 1). Отметки горизонталей, кратные высоте сечения, подписываются либо в разрыве горизонталей, либо у их концов так, чтобы нижняя часть цифр располагалась ниже по скату, указывая на понижение рельефа. Высота сечения выбирается в зависимости:

— от масштаба карты (плана): чем крупнее масштаб, тем меньше высота сечения;

— от характера местности: для горной местности высота сечения больше, чем для равнинной;

— от требуемой точности и детальности, определяемой хозяйственно-техническими соображениями: чем точнее и детальнее требуется изобразить рельеф, тем меньше должна быть высота рельефа.

Как мы уже выяснили, расстояние между соседними секущими уровенными поверхностями называется высотой сечения рельефа h. Расстояние на карте между смежными горизонталями называется заложением d. Высота сечения рельефа зависит от масштаба карты и характера рельефа местности. Нормальной высотой сечения принято считать высоту, равную 0,02 см в масштабе карты. В зависимости от условий рельефа местности для различных масштабов карт установлены стандартные нормальные высоты сечения рельефа. Так, в пределах равнинных территорий для топокарт масштаба 1:10 000 – 2,5 м; 1:25 000 – 5 м; 1:50 000 – 10 м; 1:100 000 – 20 м.

Горизонтали нормального сечения проводят сплошными линиями коричневого цвета толщиной 0,12–0,15 мм и называют основными или сплошными горизонталями. Для улучшения читаемости рельефа каждая пятая горизонталь (для масштаба 1:10 000 – каждая десятая), вычерчивается утолщенной линией 0,2 – 0,25 мм. Такие горизонтали называются утолщенными. Для отражения форм рельефа, не выражающихся основными горизонталями применяются дополнительные и вспомогательные горизонтали. Дополнительные, или полугоризонтали проводятся в половине основного сечения прерывистыми линиями длиной штрихов 5 мм, а вспомогательные или четвертьгоризонтали – в ¼ высоты сечения длиной штрихов – 2 мм. Формы рельефа, не выражающиеся горизонталями, изображаются специальными условными знаками. Это – обрывы, оползни, осыпи, овраги, промоины, воронки, курганы и др. Изображение элементов местности горизонталями представлено на рис. 3.10.

Горизонтали имеют следующие свойства:

1. Все точки, лежащие на одной горизонтали, имеют одинаковые отметки высот, кратные принятой высоте сечения рельефа.

2. Горизонтали – непрерывные замкнутые линии. Если горизонталь не замыкается внутри карты, то может обрываться только у рамки карты.

3. Горизонтали никогда не пересекаются, т. к. относятся к разным по высоте плоскостям.

4. Горизонтали одного и того же склона имеют внешнее сходство в рисунке.

5. Расстояние между горизонталями характеризует крутизну склона (ската).

Для улучшения читаемости рельефа, на карте подписываются абсолютные отметки вершин, седловин, тальвегов, перегибов склонов, а также относительные высоты обрывов, курганов, уступов террас, которые отсчитываются от подошв и бровок.

1. Отметка точки, расположенной на горизонтали, равна отметке этой горизонтали (напр., на рис. 6 Н₁=152,5 м).

2. Отметку точки, расположенной между горизонталями (напр., точки 2), определяют из выражения:

,

(1)

где Н_мл. – отметка младшей горизонтали, (Н_мл.= 150,0 м), Δh₁ – превышение точки 2 над младшей горизонталью; d–заложение ската,l₁–расстояние в плане от младшей горизонтали до точки; h – высота сечения рельефа, м.

Для приведенного на рис. 6 примера

.

Для контроля отметку точки следует определить относительно старшей горизонтали как

.

(2)

3. Отметку точки, расположенной между горизонталями с одинаковыми отметками (точка 3 – седловина) либо внутри замкнутой горизонтали (точка 4 – вершина), можно определить лишь приближенно. При этом отметку точки принимают меньше или больше отметки этой горизонтали на половину высоты сечения рельефа, т. е. 0,5 h. Например:

;

.

Превышения между точками определяют как разность отметок последующей и предыдущей отметок, т. е.

.

(3)

Определение отметок точек и превышений

Точки	Отметки точек Н, м	Превышения h, м
152,50
— 1,50
151,00
+ 2,75
153,75
+ 7,50
161,25
— 8,75
152,50

Контролем правильности вычислений является равенство нулю суммы всех превышений т. е. .

Лучшие изречения:

Студент всегда отчаянный романтик! Хоть может сдать на двойку романтизм. © Эдуард А. Асадов
==> читать все изречения. 391 — | 269 —

Источник

Определение отметки (высоты) точки

При определении высоты точки по карте могут встретиться следующие случаи:

1.Точка лежит на горизонтали. Ее отметка равна отметке горизонтали.

2.Точка М лежит между горизонталями с отметками НК и НN (Рис.1.). В этом

случае отметку точки определяют посредством интерполирования, для чего измеряют расстояния d1 и d2 от точки М до ближайших горизонталей с помощью линейки.

Отметку НМ точки М вычисляют дважды с учетом направления понижения местности:

НМ = НК + (h*d1)/( d1 + d2); НМ = НN — (h*d2)/( d1 + d2),

где НК, НN – отметки горизонталей, м ; d1 и d2 – расстояния от точки М до горизонталей, м ; h – высота сечения рельефа ( на рис.1 h = 2,5 м).

За окончательное значение принимают среднюю отметку.

3.Точка расположена внутри замкнутой горизонтали. Точка Р лежит внутри замкнутой горизонтали и является вершиной высоты. Очевидно, что ее отметка НР больше отметки горизонтали, окружающей точку, на величину, меньшую высоты сечения рельефа. Можно принять, что отметка НР приближенно равна отметке соседней горизонтали плюс половина высоты сечения рельефа, т.е. НР = 151,25 м. Если точка является дном котловины, ее отметка будет меньше высоты ближайшей горизонтали на величину, равную половине высоты сечения рельефа. Точность определения отметки точки по горизонталям на среднепересеченной местности равна примерно 1/3 высоты сечения рельефа.

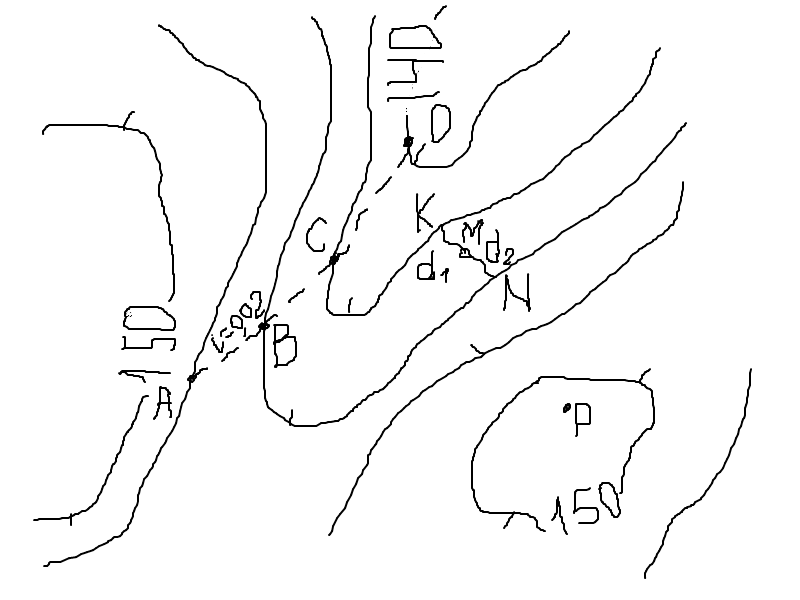
Рис.1 — Определение отметки (высоты) точки.

5) вычислить превышение точки 2 над точкой 1;

6) определить расстояние между точками 1 и 2;

7) вычислить уклон линии 1- 2;

Вычисление уклона линии.

Решение данной задачи можно выполнить двумя способами: по масштабу (графику) заложений и по приближенной формуле.

При первом способе в раствор циркуля-измерителя берется расстояние между двумя смежными горизонталями по линии наибольшей крутизны, т. е. по кратчайшему расстоянию между ними и, приложив иглы циркуля к графику заложений, определить угол наклона (рис.3). График заложений (рис.2) помещается под южной стороной рамки листа топографической карты. В случае очень близкого расположения горизонталей друг к другу, когда затруднительно взять расстояние между ними, крутизну склона определяют между утолщенными горизонталями, пользуясь при этом графиком заложений между утолщенными горизонталями (правый график заложений).

Пусть требуется определить крутизну ската вдоль отрезка ef. Взяв отрезок в раствор циркуля-измерителя, перемещаем нижнюю ножку циркуля вдоль основания основного (левого) масштаба заложений до тех пор, пока верхняя точка не окажется на кривой. В данном примере крутизна ската равна 2,5˚

Приближенная формула для определения величина угла ν, характеризующего крутизну склона, следующая: i = tg = h/d ; где h – превышение (высота сечения рельефа); d– заложение в метрах на местности. Эту формулу можно использовать для определения среднего угла наклона для двух точек, лежащих на одном склоне (рис.1).

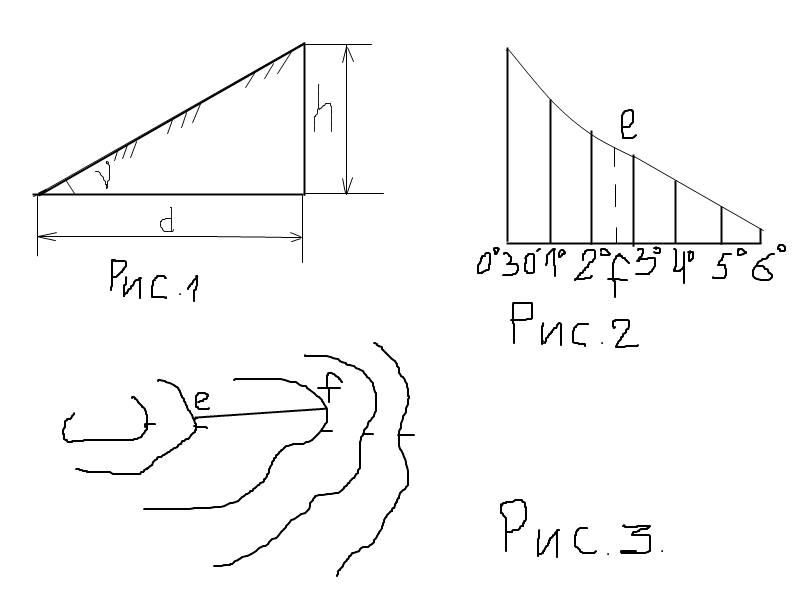
8) определить дирекционный угол линии 1 – 2 и обратный 2 – 1;

Источник

6. Определение отметок точек по горизонталям

Рассмотрим три случая:

1-й случай: точка А находится на горизонтали;

2-й случай: точки В и С находятся между горизонталями;

3-й случай: точка Д находится между точкой с отметкой и горизонталью.

Когда точка А расположена на горизонтали (1-й случай), то ее отметка равна отметке горизонтали. Отметка горизонтали может быть определена следующим образом:

– под южной рамкой карты указывается высота сечения рельефа, т.е. превышение между двумя сплошными соседними горизонталями (h_с);

– отыскиваем в районе расположения точки А подписанную горизонталь или точку с отметкой и устанавливаем, в какую сторону от точки А идет понижение рельефа. Понижение отметок рельефа можно определить по расположению бергштрихов, по надписанным горизонталям (основание цифры обращено в сторону понижения отметок) или по вторичным признакам (понижение идет к рекам, ручьям и т.д.). Зная высоту сечения рельефа h_с, производим оцифровку горизонталей (все сплошные горизонтали имеют высоты, кратные h_с; в нашем примере высоты горизонталей оканчиваются на 2,5м; 5м; 7,5 м; 0 м, горизонтали, вычерченная штрих-пунтирной линией — полугоризонталь отличается по высоте от сплошной горизонтали на ½ высоты сечения (в нашем случае на 1,25м).

В нашем случае ( рис.14) высота сечения рельефа h_с равна 2,5 м, тогда, учитывая, что точка А лежит на горизонтали, расположенной на 3 сечения выше, чем горизонталь с отметкой 100м, получим

Рис. 14. Определение отметок по горизонталям.

Сплошные горизонтали проведены через 2,5 м

Если точка расположена между горизонталями (случай 2), то вначале производят оцифровку сплошных горизонталей и полугоризонталей, так, как описано в первом случае, а затем производят интерполяцию по расстоянию до ближайшей горизонтали.

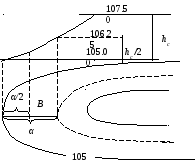
Рис. 15. Определение высоты точки В

На рис. 15 точка В расположена между сплошной горизонталью 105 м и полугоризонталью 106,25 м посередине, поэтому ее высота будет равна

Точка С расположена выше горизонтали 102,5 на величину Δh, которая находится из пропорции

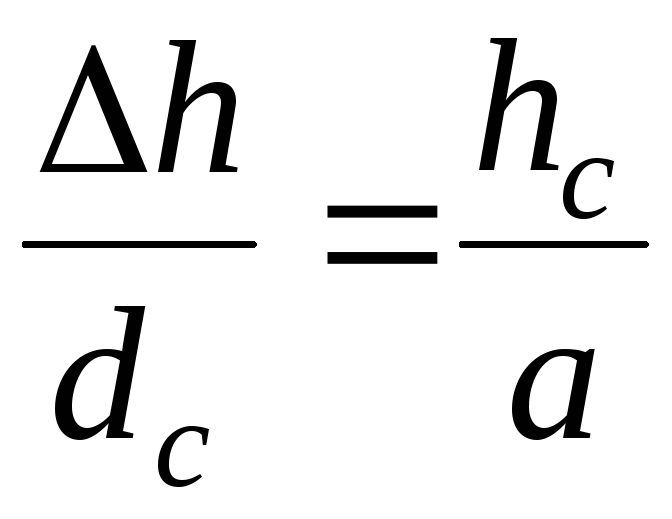, (27)

где 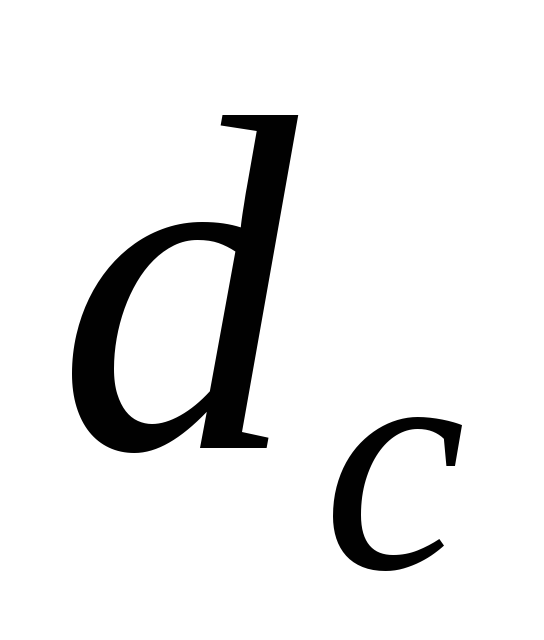– расстояние от горизонтали с отметкой 102,5м до точки С; – заложение расстояния между горизонталями в плане.

Отметка точки С будет равна:

Если точка Д находится между горизонталью и точкой К с известной отметкой (случай 3), то ее отметка находится так же, как и у точек В и C. Разница в данном случае только в том, что отметка точки К уже известна.

где

; ; .

Тогда

Построение продольного профиля по заданному направлению

На карте задано направление, например АВ, для которого необходимо построить продольный профиль (рис. 17)

Источник