Достаточно знать длину бокового ребра пирамиды, количество сторон многоугольника, лежащего в основании пирамиды, а также длину стороны основания (сторону многоугольника).
В основании правильной пирамиды всегда лежит правильный многоугольник. Любой правильный многоугольник можно вписать в окружность.
Есть такая формула:
a — длина стороны n-угольника (для правильного многоугольника).
L – длина окружности, описывающей этот многоугольник.
n – это количество сторон этого многоугольника
Если выразить эту формулу наоборот, то можно по стороне многоугольника найти длину окружности.
L=a*π/sin(180/n)
Зная длину окружности, можно найти радиус этой окружности:
L=2πR
R=L/(2π)
Подставляя L из первой формулы, получаем:
R = L/(2π) = a*π/(2π*sin(180/n)) = a/(2sin(180/n))
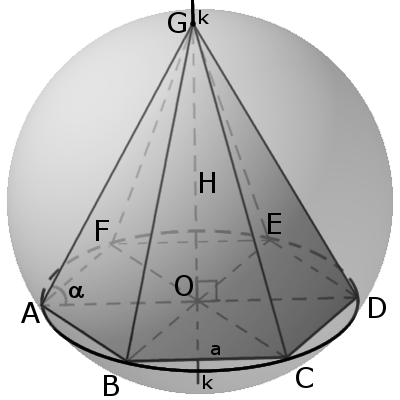
Теперь если приглядитесь к рисунку, то увидите, что радиус описанной окружности является также и катетом в прямоугольном треугольнике (игреком “y” на левой картинке).
А вертикальное ребро пирамиды это гипотенуза этого прямоугольного треугольника.
А искомая нам высота это второй катет этого прямоугольного треугольника.
По теореме Пифагора:
X²=Y²+h²
h²=X²-Y²
h=√(X²-Y²)
X нам известен – это длина боковой стороны пирамиды.
Y тоже известен – это расстояние от одного из углов основания пирамиды до центра пирамиды, и это же радиус описанной вокруг этого многоугольника окружности.
Y=R, а R равен: R=a/(2sin(180/n))
Итак подведём итог:
h=√(X²-Y²) = √(X²-R²) = √(X²-(a/(2sin(180/n)))²)
X – размер боковой стороны (ребра) пирамиды.
n – количество сторон многоугольника в основании.
a – размер стороны этого многоугольника в основании.
Более удобно эту формулу я отразил на рисунке.
Наклонная высота квадратной пирамиды – это расстояние между ее вершиной, или вершиной , до земли вдоль одной из ее сторон. Вы можете определить наклонную высоту, представив ее как один элемент треугольника. Таким образом, вы можете использовать теорему Пифагора для сравнения высоты наклона с высотой пирамиды и длиной сторон
Нахождение высоты наклона в виде треугольника
Чтобы определить высоту уклона, вы можете понимать высоту уклона как одну линию в прямоугольном треугольнике внутри пирамиды. Две другие линии треугольника будут высотой от центра пирамиды до ее вершины и линией, равной половине длины одной из сторон пирамиды, которая соединяет центр с нижней частью уклона. Длина уклона – это сторона треугольника, противоположная прямому углу – эта сторона называется гипотенузой .
Теорема Пифагора – это математическая формула, которая рассказывает, как разные стороны прямоугольного треугольника связаны друг с другом. Если a и b – две стороны, соединенные прямым углом, а c – гипотенуза, то:
а ^ 2 + б ^ 2 = с ^ 2
«^ 2» в формуле означает, что вы возводите числа в квадрат . Квадрат числа означает, что вы умножаете его на себя. Таким образом, с ^ 2 так же, как с раз с.
Нахождение высоты и базы
Если вы знаете высоту пирамиды и длину одной из сторон ее квадратного основания, вы можете использовать теорему Пифагора для определения высоты наклона. «A» и «b» в теореме будут высотой и половиной длины одной стороны, а «c» будет высотой наклона, поскольку высота наклона является гипотенузой треугольника:
высота ^ 2 + половина длины ^ 2 = наклонная высота ^ 2
Скажем, у вас есть пирамида высотой 4 дюйма и квадратное основание со сторонами 6 дюймов в длину. Чтобы найти половину длины стороны, разделите длину стороны на 2. Таким образом, эта пирамида будет иметь высоту 4 дюйма и половину длины 3 дюйма.
Выравнивание высоты и основания
В теореме Пифагора квадрат гипотенузы равен сумме квадратов двух других сторон. Теперь возведите в квадрат высоту и половину длины и сложите квадратные числа вместе.
Возьмите пирамиду с высотой 4 дюйма и половиной длины 3 дюйма. Квадраты 4 и 3. Помните, что число в квадрате – это число, умноженное на себя. Так:
4 ^ 2 + 3 ^ 2 = высота наклона ^ 2 4 x 4 + 3 x 3 = высота наклона ^ 2
Затем вы добавляете эти два числа вместе:
16 + 9 = высота наклона ^ 2 25 = высота наклона ^ 2
Таким образом, наклонная высота в квадрате равна 25.
Принимая квадратный корень
Теперь вы знаете, что квадрат наклонной высоты – или умноженный на нее – равен 25. Чтобы найти высоту наклонной части, найдите число, умноженное на себя, равное 25. Это называется взятием квадратного корня из 25. Если вы проверяете малые числа, умноженные на себя, вы обнаружите, что 5 умножить на 5 равно 25. Итак:
5 дюймов = наклонная высота
Не всегда можно найти квадратные корни чисел, угадывая и проверяя. Многие числа не имеют точных квадратных корней, поэтому вам может понадобиться калькулятор, чтобы найти приближение.
Необходимо построить наклонную пирамиды по известному основанию и высоте.
Для решения задачи необходимо знать теоретический материал:
— способы восстановления перпендикуляра к плоскости;
— определение натуральных величин методом вращения;
— определение видимости на чертеже с помощью конкурирующих точек (рассматривали в задаче 1).
Порядок решения задачи
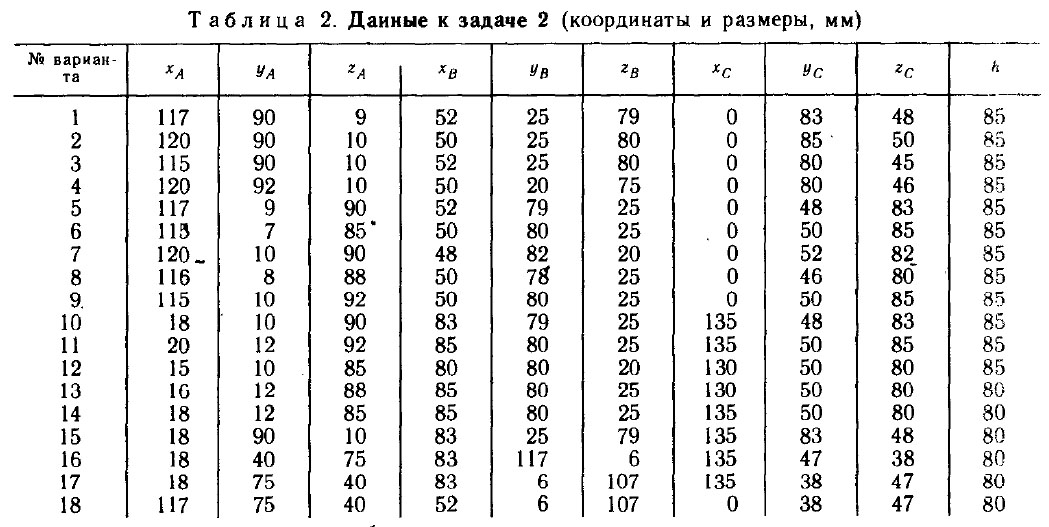
1. Согласно варианту задания наносим на комплексный чертеж координаты точек основания пирамиды, получаем плоскость в виде треугольника ABC(A’B’C’; ABC) (рис.2.1.a).

Рис. 2.1
2. Для нахождения вершины пирамиды по заданной высоте необходимо к указанной плоскости провести перпендикуляр через точку А (A’; A) т.к. величина высоты задана SA, для чего:
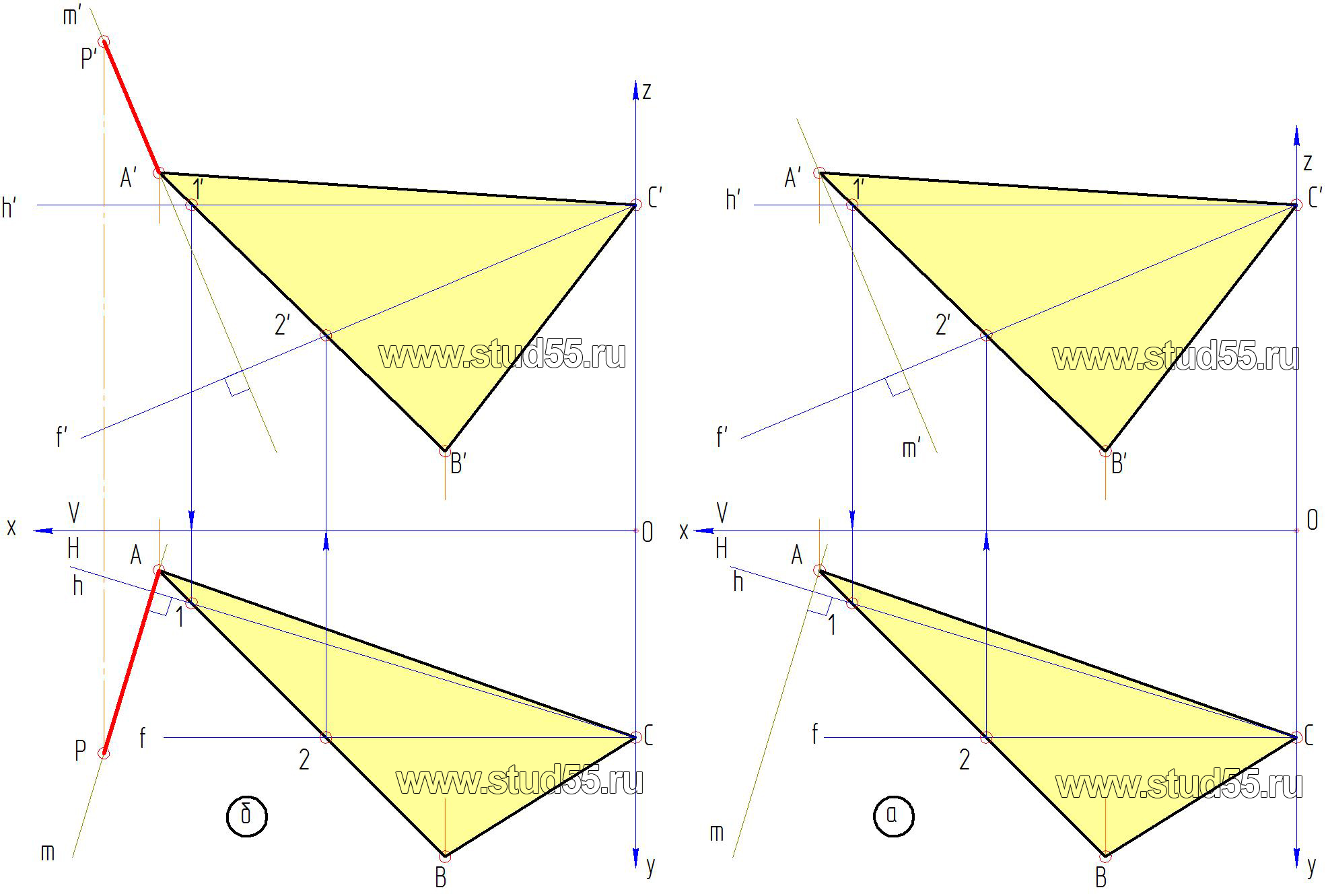
— в заданной плоскости треугольника основания пирамиды проводим горизонталь h’и h и фронталь – f’ и f (рис.2.1.б).
— к проекциям горизонтали и фронтали, которые выражены в натуральной величине через точку А(A’; A) проводим перпендикуляр m (рис.2.2.а).
Рис.2.2
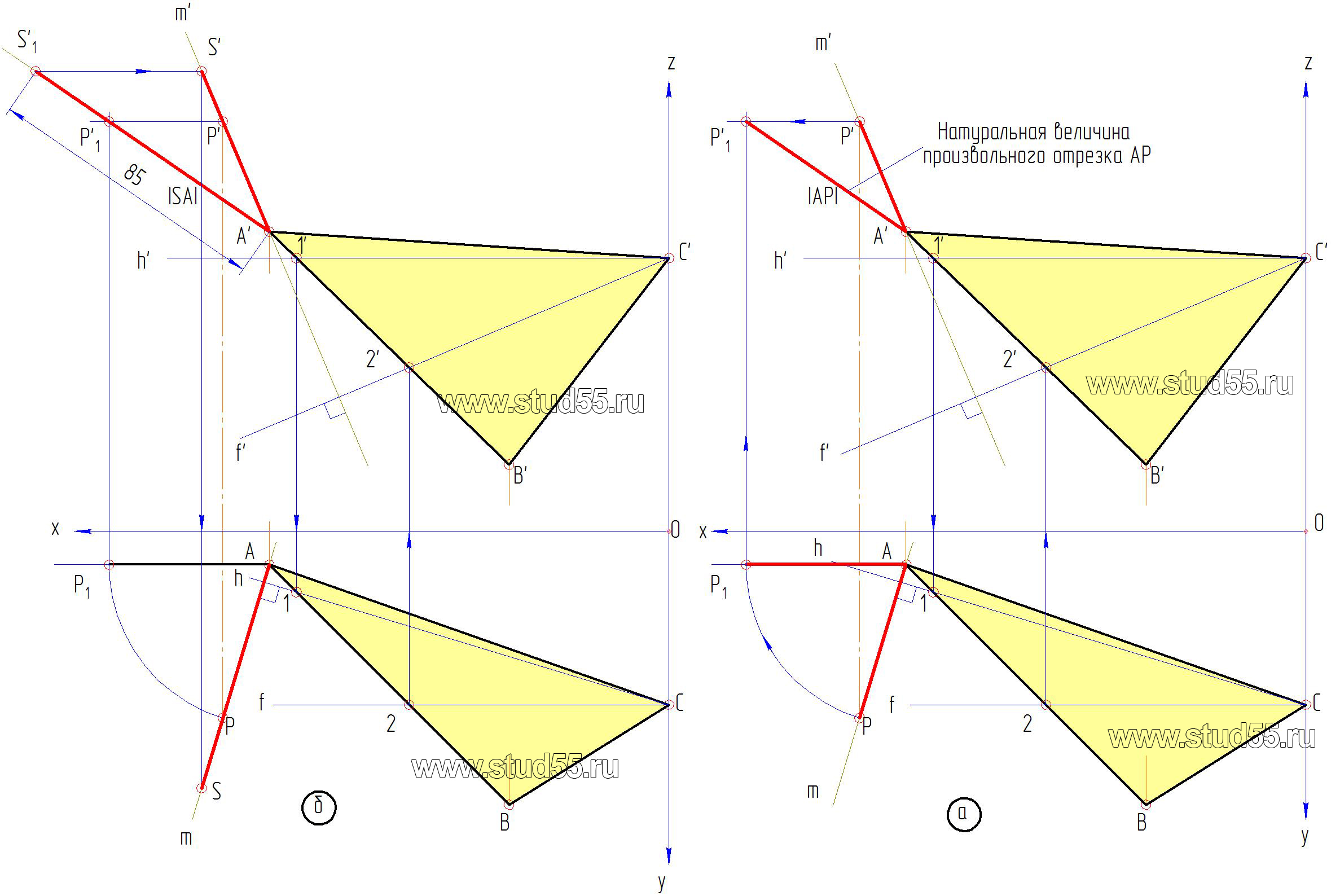
3. Так как высота пирамиды задана в натуральной величине, а проведенный перпендикуляр — в проекциях, необходимо получить линию натуральной величины произвольного отрезка на перпендикуляре. Для этого воспользуемся методом вращения:
-на проекциях перпендикуляра возьмем произвольную точку P (P’ и Р) (рис.2.2.б);
— отрезок AР в горизонтальной проекции переведем в частное положение путем разворота его вокруг точки A, до параллельности оси х, получим точку P1 (рис.2.3.а).
— можно отметить, что при вращении точки в какой-то плоскости ее проекция на сопряженной плоскости движется по прямой параллельной оси х. Проведем ее из точки P’ и тогда по линиям связи на ней находим фронтальную проекцию точки P —P’1
— соединив P’1 и A’ получим линию натуральной величины отрезка перпендикуляра, на котором откладываем заданное расстояние SA (h=85мм), получая S’1 — истинное положение вершины пирамиды.
4. Переведем истинную вершину пирамиды S’1 на фронтальную проекцию перпендикуляра по линии параллельной оси х получаем S’ — фронтальную проекцию вершины пирамиды. По линии связи получаем ее горизонтальную проекцию – S (рис.2.3.б).
Рис.2.3
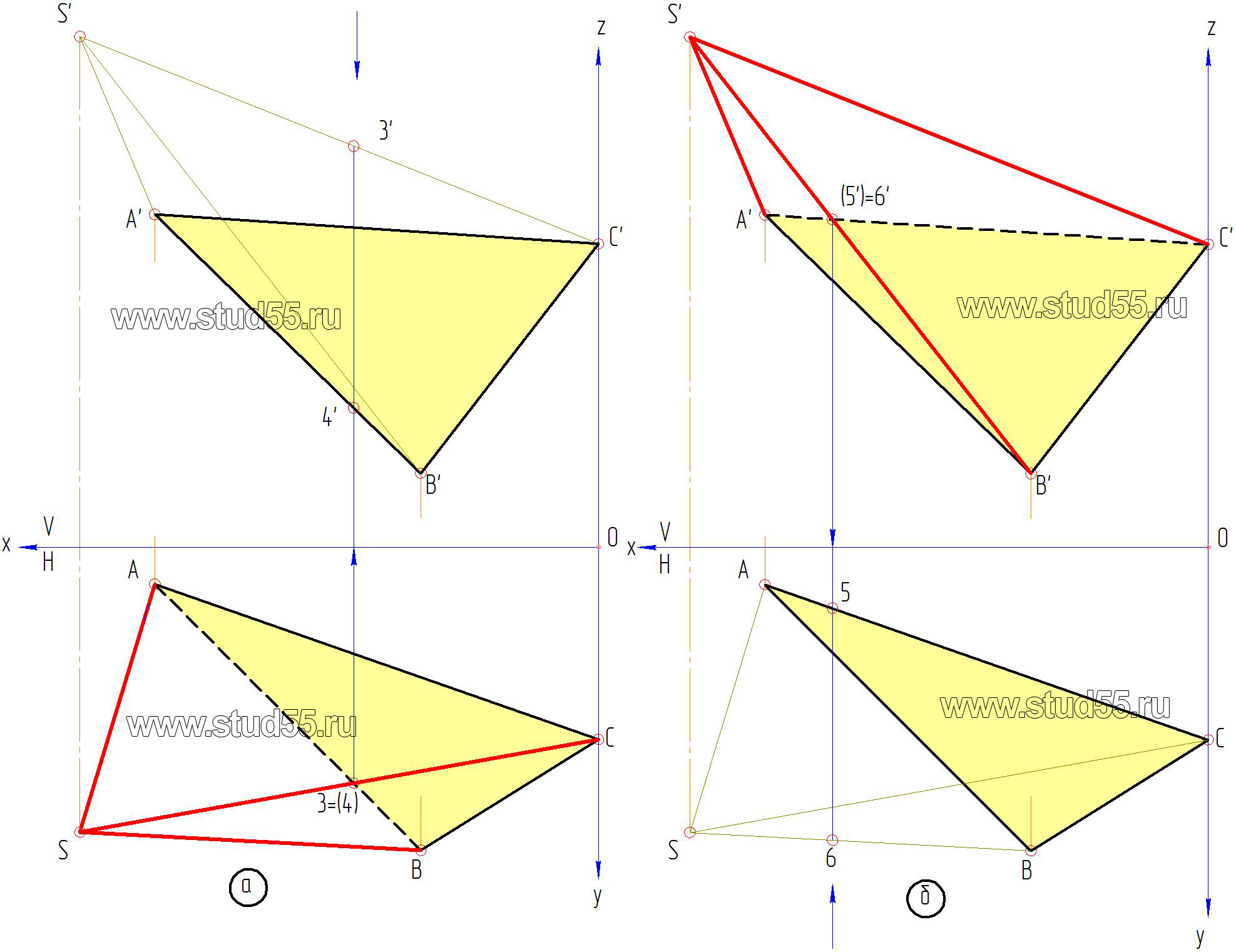
5. Таким образом, вершина пирамиды S (S’ и S) построена, соединяем ее с основанием и в заключение определяем видимость ребер пирамиды, для чего:
— возьмем на горизонтальной проекции две конкурирующие точки 3 и 4, принадлежащие соответственно линиям SC и AB спроецируем данные точки на фронтальную плоскость, получим 3’ и 4’ на линиях S’C’ и A’B’;
— по правилу определения видимости с помощью конкурирующих точек определяем, что прямая SC, в горизонтальной проекции будет видимой, т.к. ордината точки 3’, находящаяся на ней во фронтальной плоскости больше, чем ордината точки 4’, а линия AB будет невидимой (рис.2.4.а);
— аналогично определяем видимость во фронтальной плоскости, беря пару конкурирующих точек 5’ и 6’, находящихся на прямых S’B’ и A’C’. По выше изложенному правилу S’B’ на фронтальной плоскости проекций будет видимой, а A’C’–невидимой (рис.2.4.б).
Рис.2.4
Рис.2.5
У меня есть все готовые решения задач с такими координатами, купить можно >>здесь<<
Купленные чертежи по начертательной геометрии из книжки Фролова Вы легко можете скачать сразу после оплаты или я вышлю Вам на почту. Они находятся в ZIP архиве в различных форматах:
*.jpg – обычный цветной рисунок чертежа в масштабе 1 к 1 в хорошем разрешении 300 dpi;
*.cdw – формат программы Компас 12 и выше или версии LT;
*.dwg и .dxf — формат программы AUTOCAD, nanoCAD;
Раздел: Начертательная геометрия /
- Рекомендуем
- Комментарии
- Наши товары
Многогранник, одна грань которого является (n)-угольником, а остальные грани — треугольники с общей вершиной, называется пирамидой, (n)-угольник называется основанием пирамиды, а треугольники — боковыми гранями.
Общая вершина боковых граней называется вершиной пирамиды.
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются рёбрами пирамиды.
В зависимости от количества сторон основания пирамиды могут быть треугольными, четырёхугольными, пятиугольными и т. д.
Перпендикуляр, проведённый из вершины пирамиды к плоскости основания, называется высотой пирамиды.
Важно знать, где на плоскости основания находится проекция вершины пирамиды, она может быть в центре основания, на стороне основания, за пределами многоугольника основания. Решение задачи в большей степени зависит от расположения этой точки.
Чтобы нарисовать пирамиду, нужно соблюдать определённый порядок:
1. первым рисуется основание,
2. по условию задачи находится проекция вершины на плоскости основания,
3. вертикально проводится высота,
4. проводятся рёбра.
На рисунке изображена четырёхугольная пирамида (SABCD)
(первой пишут букву вершины).
Основание — четырёхугольник (ABCD).
Вершина проецируется в точку пересечения диагоналей (O) — основание высоты или проекция вершины.
(SA), (SB), (SC), (SD) — рёбра пирамиды,
(AB), (BC), (CD), (DA) — стороны основания.
В курсе средней школы в основном есть задачи, в которых даны:
– правильная пирамида (вершина проецируется в центр основания);
– пирамида, вершина которой проецируется в центр описанной окружности;
– пирамида, вершина которой проецируется в центр вписанной окружности;
– пирамида, высота которой совпадает с боковым ребром;
– пирамида, высота которой также является высотой боковой грани.
Углы, которые образованы боковой гранью и основанием пирамиды, называются двугранными углами при основании пирамиды.
Двугранный угол между боковой гранью (SCD) и гранью основания равен линейному углу
∠
(OES). Этот угол образован отрезками (OE) и (SE), лежащими в этих гранях и перпендикулярных их общей прямой (CD). То есть (OE)
⊥CD
и (SE)
⊥CD
.
Чтобы определить этот угол, часто нужно использовать теорему о трёх перпендикулярах.
Углы, которые образованы боковым ребром и его проекцией на плоскость основания, называются углами между боковым ребром и плоскостью основания.
На рисунке
∠
(OCS).
Угол, который образован двумя боковыми гранями, называется двугранным углом при боковом ребре пирамиды.
Угол, который образован двумя боковыми рёбрами одной грани пирамиды, называется углом при вершине пирамиды.
Основные формулы пирамиды
Площадь боковой поверхности равна сумме площадей всех боковых граней пирамиды:
S=S1+S2+S3+…
(Некоторые формулы годятся только для определённых видов пирамиды.)
Площадь полной поверхности
Sп.п.=S+Sоснования
.
Объём пирамиды (V =)
13Sоснования
(H), где (H) — высота пирамиды.
Формула объёма используется для пирамид любого вида.
Источники:
Рис. 1. Пирамида, © ЯКласс.
Пирамида. Формулы и свойства пирамиды
Определение.
Пирамида — это многогранная объемная фигура, ограниченная плоским многоугольником (основой) и треугольниками, имеющих общую вершину, не лежащую в плоскости основания.
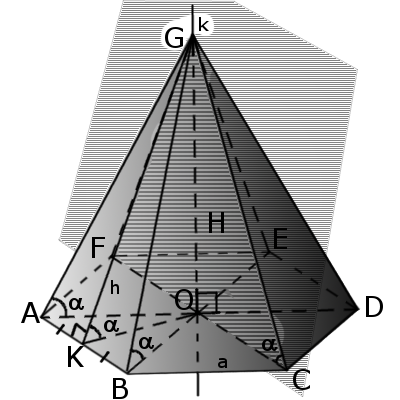 |
| Рис.1 |
Определение. Боковая грань – это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).
Определение. Боковые ребра – это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
Определение. Высота пирамиды – это перпендикуляр, опущенный из вершины на основание пирамиды.
Определение. Апофема – это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.
Определение. Диагональное сечение – это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение. Правильная пирамида – это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.
Объём и площадь поверхности пирамиды
Формула. Объём пирамиды через площадь основы и высоту:
Определение. Боковая поверхность пирамиды – это совокупная площадь всех боковых граней пирамиды.
Определение. Полная поверхность пирамиды – это совокупность площадей боковой поверхности и площади основания пирамиды.
Формула. Площадь боковой поверхности правильной пирамиды через периметр основания и апофему:
Свойства пирамиды
Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.
Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.
Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.
Свойства правильной пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые ребра наклонены под одинаковыми углами к основанию.
4. Апофемы всех боковых граней равны.
5. Площади всех боковых граней равны.
6. Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.
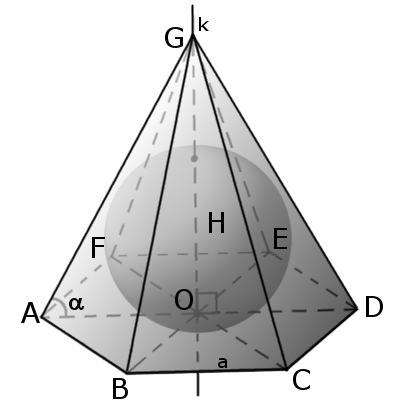
8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n, где n – это количество углов в основании пирамиды.
Связь пирамиды со сферой
Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Связь пирамиды с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.
Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.
Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.
Связь пирамиды с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.
Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.
Определение. Усеченная пирамида (пирамидальная призма) – это многогранник, который находится между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом пирамида имеет большую основу и меньшую основу, которая подобна большей. Боковые грани представляют собой трапеции.
Определение. Треугольная пирамида (четырехгранник) – это пирамида в которой три грани и основание являются произвольными треугольниками.
В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол.
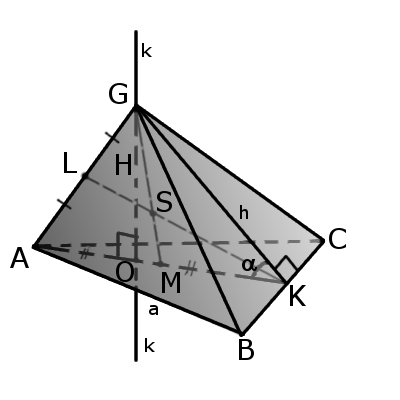
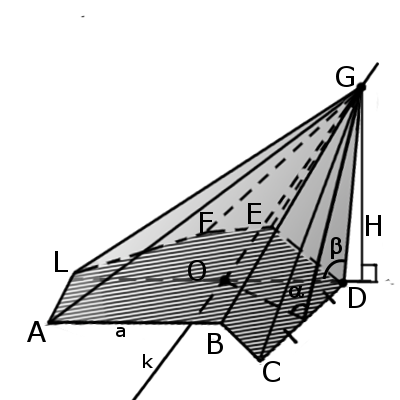
Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника (GM).
Бимедианой называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.
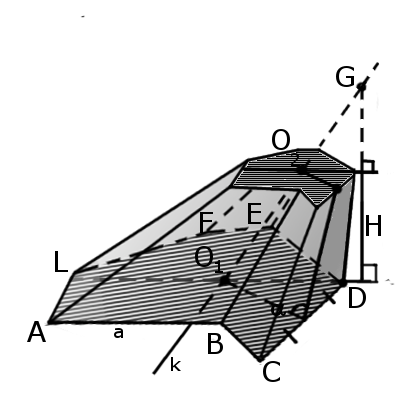
Определение. Наклонная пирамида – это пирамида в которой одно из ребер образует тупой угол (β) с основанием.
Определение. Прямоугольная пирамида – это пирамида в которой одна из боковых граней перпендикулярна к основанию.
Определение. Остроугольная пирамида – это пирамида в которой апофема больше половины длины стороны основания.
Определение. Тупоугольная пирамида – это пирамида в которой апофема меньше половины длины стороны основания.
Определение. Правильный тетраэдр – четырехгранник у которого все четыре грани – равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.
Определение. Прямоугольный тетраэдр называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Определение. Равногранный тетраэдр называется четырехгранник у которого боковые грани равны между собой, а основание – правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.
Определение. Ортоцентричный тетраэдр называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.
Определение. Звездная пирамида называется многогранник у которого основой является звезда.
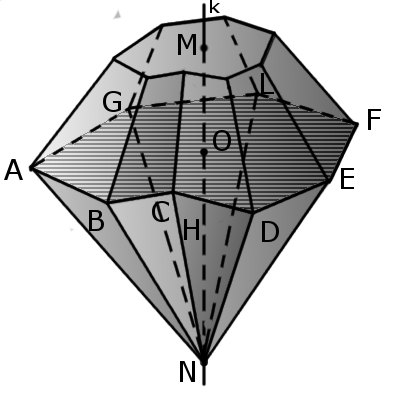
Определение. Бипирамида – многогранник, состоящий из двух различных пирамид (также могут быть срезаны пирамиды), имеющих общую основу, а вершины лежат по разные стороны от плоскости основания.