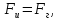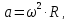Как найти высоту орбиты вокруг земли

Вычисление параметров геостационарной орбиты Радиус орбиты и высота орбиты

На геостационарной
орбите спутник не приближается к Земле
и не удаляется от неё, и кроме того,
вращаясь вместе с Землёй, постоянно
находится над какой-либо точкой на
экваторе. Следовательно, действующие
на спутник силы гравитации и центробежная
сила должны уравновешивать друг друга.
Для вычисления высоты геостационарной
орбиты можно воспользоваться методами
классической механики и, перейдя в
систему отсчета спутника, исходить из
следующего уравнения:

где
– сила инерции, а в данном случае,
центробежная сила;– гравитационная сила. Величину
гравитационной силы, действующую на
спутник, можно определить по закону
всемирного тяготения Ньютона:

где
– масса спутника,– масса Земли в килограммах,– гравитационная постоянная, а– радиус орбиты (расстояние в метрах
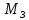
от спутника до центра Земли).

Величина центробежной
силы равна:

где
– центростремительное ускорение,
возникающее при круговом движении по
орбите.

Как можно видеть,
масса спутника присутствует в выражениях
и для центробежной силы, и для гравитационной
силы. То есть, высота орбиты не зависит
от массы спутника, что справедливо для
любых орбит и является следствием
равенства гравитационной и инертной
массы. Следовательно, геостационарная
орбита определяется лишь высотой, при
которой центробежная сила будет равна
по модулю и противоположна по направлению
гравитационной силе, создаваемой
притяжением Земли на данной высоте.

Центростремительное
ускорение равно:

где
– угловая скорость вращения спутника,
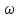
в радианах в секунду.

Исходя из равенства
гравитационной и центробежной сил,
получаем:

Отсюда
.

Угловая скорость
ωвычисляется делением угла,
пройденного за один оборот на период
обращения (время, за которое совершается
один полный оборот по орбите: один
сидерический день, или 86 164 секунды).
Получаем:рад/с

Расчетный радиус
орбиты составляет 42 164 км. Вычитая
экваториальный радиус Земли, 6 378 км,
получаем высоту ГСО 35 786 км.

Орбитальная скорость

Скорость движения
по геостационарной орбите вычисляется
умножением угловой скорости на радиус
орбиты:
км/с

Это примерно в 2.5
раза меньше, чем первая космическая
скорость равная 8 км/с для околоземной
орбиты (с радиусом 6400 км). Так как квадрат
скорости для круговой орбиты обратно
пропорционален её радиусу, то уменьшение
скорости по отношению к первой космической
достигается увеличением радиуса орбиты
более чем в 6 раз.

Длина орбиты

Длина геостационарной
орбиты:
.
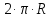
При радиусе орбиты 42 164 км получаем
длину орбиты 264 924 км. Длина орбиты
крайне важна для вычисления «точек
стояния» спутников.

Удержание спутника
в орбитальной позиции на геостационарной
орбите. Спутник, обращающийся на
геостационарной орбите, находится под
воздействием ряда сил (возмущений),
изменяющих параметры этой орбиты. В
частности, к таким возмущениям относятся
гравитационные лунно-солнечные
возмущения, влияние неоднородности
гравитационного поля Земли, эллиптичность
экватора и т.д. Деградация орбиты
выражается в двух основных явлениях:

1) Спутник смещается
вдоль орбиты от своей первоначальной
орбитальной позиции в сторону одной из
четырёх точек стабильного равновесия,
так называемых «потенциальных ям
геостационарной орбиты» (их долготы
75,3°E, 104,7°W, 165,3°E, и 14,7°W) над экватором
Земли;

2) Наклонение орбиты
к экватору увеличивается (от первоначального
=0) со скоростью порядка 0,85 градусов в
год и достигает максимального значения
15 градусов за 26,5 лет.

Для компенсации
этих возмущений и удержания спутника
в назначенной точке стояния спутник
оснащается двигательной установкой
(химической или электроракетной).
Периодическими включениями двигателей
малой тяги (коррекция «север-юг» для
компенсации роста наклонения орбиты и
«запад-восток» для компенсации дрейфа
вдоль орбиты) спутник удерживается в
назначенной точке стояния. Такие
включения производятся по нескольку
раз в несколько (10—15) суток. Существенно,
что для коррекции «север-юг» требуется
значительно большее приращение
характеристической скорости (около
45—50 м/с в год), чем для долготной коррекции
(около 2 м/с в год). Для обеспечения
коррекции орбиты спутника на протяжении
всего срока его эксплуатации (12—15 лет
для современных телевизионных спутников)
требуется значительный запас топлива
на борту (сотни килограммов, в случае
применения химического двигателя).
Химический ракетный двигатель спутника
имеет вытеснительную систему подачи
топлива (газ наддува – гелий), работает
на долгохранимых высококипящих
компонентах (обычно несимметричный
диметилгидразин и азотный тетраксид).
На ряде спутников устанавливаются
плазменные двигатели. Их тяга существенно
меньше, чем у химических, однако большая
эффективность позволяет (за счет
продолжительной работы, измеряемой
десятками минут для единичного маневра)
радикально снизить потребную массу
топлива на борту. Выбор типа двигательной
установки определяется конкретными
техническими особенностями аппарата.

Эта же двигательная
установка используется, при необходимости,
для маневра перевода спутника в другую
орбитальную позицию. В некоторых случаях
– как правило, в конце срока эксплуатации
спутника, для сокращения расхода топлива
коррекция орбиты «север-юг» прекращается,
а остаток топлива используется только
для коррекции «запад-восток». Запас
топлива является основным лимитирующим
фактором срока службы спутника на
геостационарной орбите.

Соседние файлы в папке 02-12-2014_07-07-59

• #
• #

Высота орбиты
спутника

Подобно тому, как места в театре позволяют по-разному взглянуть на представление, различные орбиты спутников дают перспективу, каждая из которых имеет свое назначение. Одни кажутся висящими над точкой поверхности, они обеспечивают постоянный обзор одной стороны Земли, в то время как другие кружат вокруг нашей планеты, за день проносясь над множеством мест.

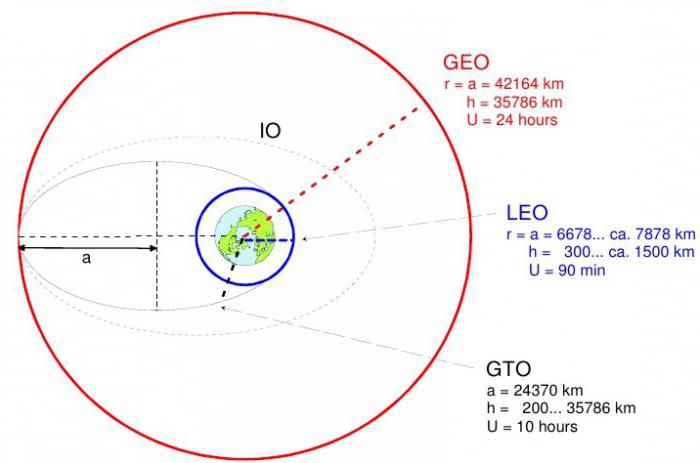
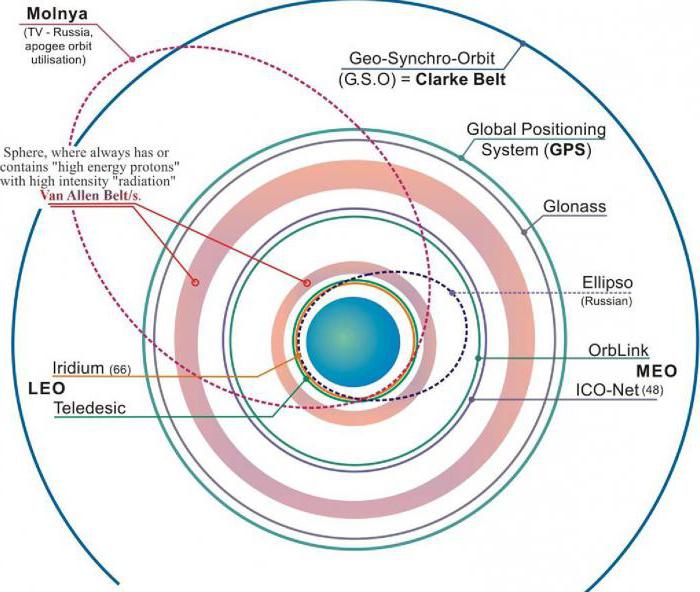
Типы орбит

На какой высоте летают спутники? Различают 3 типа околоземных орбит: высокие, средние и низкие. На высокой, наиболее удаленной от поверхности, как правило, находятся многие погодные и некоторые спутники связи. Сателлиты, вращающиеся на средней околоземной орбите, включают навигационные и специальные, предназначенные для мониторинга конкретного региона. Большинство научных космических аппаратов, в том числе флот системы наблюдения за поверхностью Земли НАСА, находится на низкой орбите.

От того, на какой высоте летают спутники, зависит скорость их движения. По мере приближения к Земле гравитация становится все сильнее, и движение ускоряется. Например, спутнику НАСА Aqua требуется около 99 минут, чтобы облететь вокруг нашей планеты на высоте около 705 км, а метеорологическому аппарату, удаленному на 35 786 км от поверхности, для этого потребуется 23 часа, 56 минут и 4 секунды. На расстоянии 384 403 км от центра Земли Луна завершает один оборот за 28 дней.

Аэродинамический парадокс

Изменение высоты спутника также изменяет его скорость движения по орбите. Здесь наблюдается парадокс. Если оператор спутника хочет повысить его скорость, он не может просто запустить двигатели для ускорения. Это увеличит орбиту (и высоту), что приведет к уменьшению скорости. Вместо этого следует запустить двигатели в направлении, противоположном направлению движения спутника, т. е. совершить действие, которое на Земле бы замедлило движущееся транспортное средство. Такое действие переместит его ниже, что позволит увеличить скорость.

Характеристики орбит

В дополнение к высоте, путь движения спутника характеризуется эксцентриситетом и наклонением. Первый относится к форме орбиты. Спутник с низким эксцентриситетом движется по траектории, близкой к круговой. Эксцентричная орбита имеет форму эллипса. Расстояние от космического аппарата до Земли зависит от его положения.

Наклонение – это угол орбиты по отношению к экватору. Спутник, который вращается непосредственно над экватором, имеет нулевой наклон. Если космический аппарат проходит над северным и южным полюсами (географическими, а не магнитными), его наклон составляет 90°.

Все вместе – высота, эксцентриситет и наклонение – определяют движение сателлита и то, как с его точки зрения будет выглядеть Земля.

Высокая околоземная

Когда спутник достигает ровно 42164 км от центра Земли (около 36 тыс. км от поверхности), он входит в зону, где его орбита соответствует вращению нашей планеты. Поскольку аппарат движется с той же скоростью, что и Земля, т. е. его период обращения равен 24 ч, кажется, что он остается на месте над единственной долготой, хотя и может дрейфовать с севера на юг. Эта специальная высокая орбита называется геосинхронной.

Спутник движется по круговой орбите прямо над экватором (эксцентриситет и наклонение равны нулю) и относительно Земли стоит на месте. Он всегда расположен над одной и той же точкой на ее поверхности.

Геостационарная орбита чрезвычайно ценна для мониторинга погоды, так как спутники на ней обеспечивают постоянный обзор одного и того же участка поверхности. Каждые несколько минут метеорологические аппараты, такие как GOES, предоставляют информацию об облаках, водяном паре и ветрах, и этот постоянный поток информации служит основой для мониторинга и прогнозирования погоды.

Кроме того, геостационарные аппараты могут быть полезны для коммуникации (телефонии, телевидения, радио). Спутники GOES обеспечивают работу поисково-спасательного радиомаяка, используемого для помощи в поиске кораблей и самолетов, терпящих бедствие.

Наконец, многие высокоорбитальные сателлиты Земли занимаются мониторингом солнечной активности и отслеживают уровни магнитного поля и радиации.

Вычисление высоты ГСО

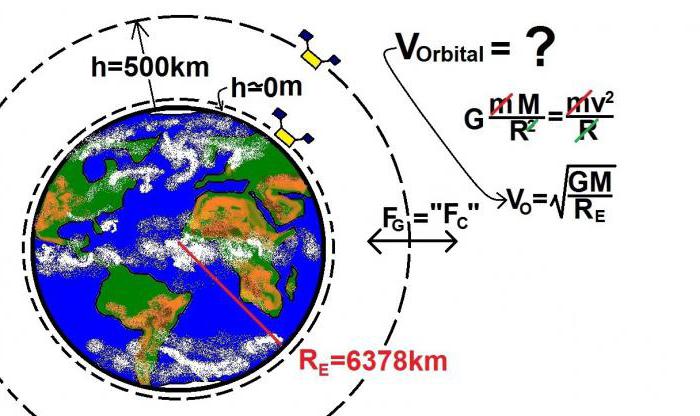
На спутник действует центростремительная сила F_ц=(M₁v²)/R и сила тяжести F_т=(GM₁M₂)/R². Так как эти силы одинаковы, можно уравнять правые части и сократить их на массу M₁. В результате получится равенство v²=(GM²)/R. Отсюда скорость движения v=((GM₂)/R)^1/2

Так как геостационарная орбита представляет собой окружность длиной 2πr, орбитальная скорость равна v=2πR/T.

Отсюда R³=T²GM/(4π²).

Так как T=8,64×10⁴с, G=6,673×10^-11 Н·м²/кг², M=5,98×10²⁴ кг, то R=4,23×10⁷ м. Если вычесть из R радиус Земли, равный 6,38×10⁶ м, можно узнать, на какой высоте летают спутники, висящие над одной точкой поверхности – 3,59×10⁷ м.

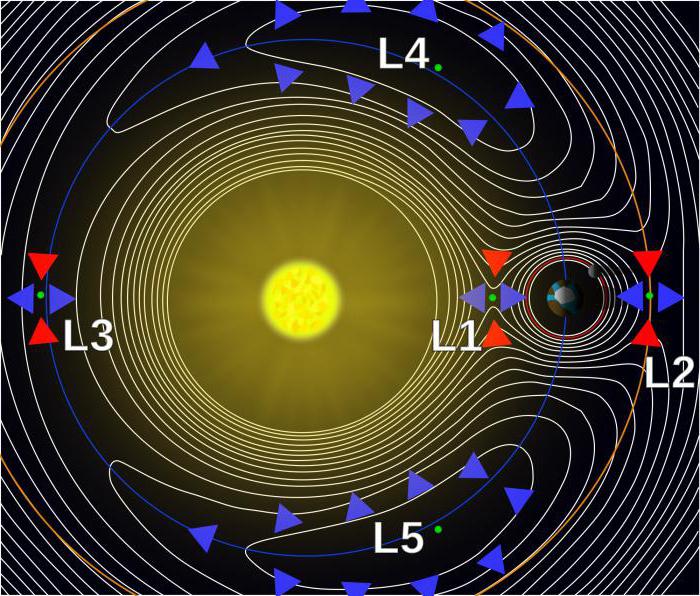
Точки Лагранжа

Другими замечательными орбитами являются точки Лагранжа, где сила притяжения Земли компенсируется силой тяжести Солнца. Все, что там находится, в равной степени притягивается к этим небесным телам и вращается с нашей планетой вокруг светила.

Из пяти точек Лагранжа в системе Солнце-Земля только две последних, называемых L4 и L5, являются стабильными. В остальных спутник подобен мячу, балансирующему на вершине крутого холма: любое незначительное возмущение будет выталкивать его. Чтобы оставаться в сбалансированном состоянии, космические аппараты здесь нуждаются в постоянной корректировке. В последних двух точках Лагранжа спутники уподобляются шару в шаре: даже после сильного возмущения они вернутся обратно.

L1 расположена между Землей и Солнцем, позволяет сателлитам, находящимся в ней, иметь постоянный обзор нашего светила. Солнечная обсерватория SOHO, спутник НАСА и Европейского космического агентства следят за Солнцем из первой точки Лагранжа, в 1,5 млн км от нашей планеты.

L2 расположена на том же расстоянии от Земли, но находится позади нее. Спутникам в этом месте требуется только один тепловой экран, чтобы защититься от света и тепла Солнца. Это хорошее место для космических телескопов, используемых для изучения природы Вселенной путем наблюдения фона микроволнового излучения.

Третья точка Лагранжа расположена напротив Земли с другой стороны Солнца, так что светило всегда находится между ним и нашей планетой. Спутник в этом положении не будет иметь возможность общаться с Землей.

Чрезвычайно стабильны четвертая и пятая точки Лагранжа в орбитальной траектории нашей планеты в 60° впереди и позади Земли.

Средняя околоземная орбита

Находясь ближе к Земле, спутники двигаются быстрее. Различают две средние околоземные орбиты: полусинхронную и «Молнию».

На какой высоте летают спутники, находящиеся на полусинхронной орбите? Она почти круглая (низкий эксцентриситет) и удалена на расстояние 26560 км от центра Земли (около 20200 км над поверхностью). Сателлит на этой высоте совершает полный оборот за 12 ч. По мере его движения Земля вращается под ним. За 24 ч он пересекает 2 одинаковые точки на экваторе. Эта орбита последовательна и весьма предсказуема. Используется системой глобального позиционирования GPS.

Орбита «Молния» (наклонение 63,4°) используется для наблюдения в высоких широтах. Геостационарные спутники привязаны к экватору, поэтому они не подходят для дальних северных или южных регионов. Эта орбита весьма эксцентрична: космический аппарат движется по вытянутому эллипсу с Землей, расположенной близко к одному краю. Так как спутник ускоряется под действием силы тяжести, он движется очень быстро, когда находится близко к нашей планете. При удалении его скорость замедляется, поэтому он больше времени проводит на вершине орбиты в самом дальнем от Земли краю, расстояние до которого может достигать 40 тыс. км. Период обращения составляет 12 ч, но около двух третей этого времени спутник проводит над одним полушарием. Подобно полусинхронной орбите сателлит проходит по одному и тому же пути через каждые 24 ч. Используется для связи на крайнем севере или юге.

Низкая околоземная

Большинство научных спутников, многие метеорологические и космическая станция находятся на почти круговой низкой околоземной орбите. Их наклон зависит от того, мониторингом чего они занимаются. TRMM был запущен для мониторинга осадков в тропиках, поэтому имеет относительно низкое наклонение (35°), оставаясь вблизи экватора.

Многие из спутников системы наблюдения НАСА имеют почти полярную высоконаклонную орбиту. Космический аппарат движется вокруг Земли от полюса до полюса с периодом 99 мин. Половину времени он проходит над дневной стороной нашей планеты, а на полюсе переходит на ночную.

По мере движения спутника под ним вращается Земля. К тому времени, когда аппарат переходит на освещенный участок, он находится над областью, прилегающей к зоне прохождения своей последней орбиты. За 24-часовой период полярные спутники покрывают большую часть Земли дважды: один раз днем и один раз ночью.

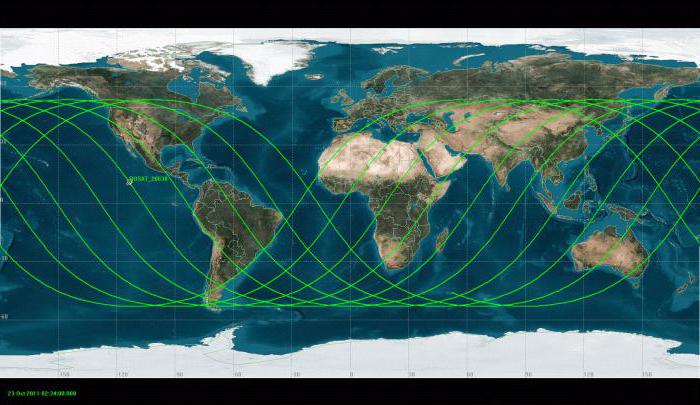
Солнечно-синхронная орбита

Подобно тому как геосинхронные спутники должны находиться над экватором, что позволяет им оставаться над одной точкой, полярно-орбитальные имеют способность оставаться в одном времени. Их орбита является солнечно-синхронной – при пересечении космическим аппаратом экватора местное солнечное время всегда одно и то же. Например, спутник Terra пересекает его над Бразилией всегда в 10:30 утра. Следующее пересечение через 99 мин над Эквадором или Колумбией происходит также в 10:30 по местному времени.

Солнечно-синхронная орбита необходима для науки, так как позволяет сохранять угол падения солнечного света на поверхность Земли, хотя он будет меняться в зависимости от сезона. Такое постоянство означает, что ученые могут сравнивать изображения нашей планеты одного времени года в течение нескольких лет, не беспокоясь о слишком больших скачках в освещении, которые могут создать иллюзию изменений. Без солнечно-синхронной орбиты было бы сложно отслеживать их с течением времени и собирать информацию, необходимую для изучения изменений климата.

Путь спутника здесь очень ограничен. Если он находится на высоте 100 км, орбита должна иметь наклон 96°. Любое отклонение будет недопустимым. Поскольку сопротивление атмосферы и сила притяжения Солнца и Луны изменяют орбиту аппарата, ее необходимо регулярно корректировать.

Выведение на орбиту: запуск

Запуск спутника требует энергии, количество которой зависит от расположения места старта, высоты и наклона будущей траектории его движения. Чтобы добраться до удаленной орбиты, требуется затратить больше энергии. Спутники со значительным наклоном (например, полярные) более энергозатратны, чем те, которые кружат над экватором. Выведению на орбиту с низким наклоном помогает вращение Земли. Международная космическая станция движется под углом 51,6397°. Это необходимо для того, чтобы космическим челнокам и российским ракетам было легче добраться до нее. Высота МКС – 337–430 км. Полярные спутники, с другой стороны, от импульса Земли помощи не получают, поэтому им требуется больше энергии, чтобы подняться на такое же расстояние.

Корректировка

После запуска спутника необходимо приложить усилия, чтобы удержать его на определенной орбите. Поскольку Земля не является идеальной сферой, ее гравитация в некоторых местах сильнее. Эта неравномерность, наряду с притяжением Солнца, Луны и Юпитера (самой массивной планеты Солнечной системы), изменяет наклон орбиты. На протяжении всего своего срока службы положение спутников GOES корректировалось три или четыре раза. Низкоорбитальные аппараты НАСА должны регулировать свой наклон ежегодно.

Кроме того, на околоземные спутники оказывает воздействие атмосфера. Самые верхние слои, хотя и достаточно разрежены, оказывают достаточно сильное сопротивление, чтобы притягивать их ближе к Земле. Действие силы тяжести приводит к ускорению спутников. Со временем они сгорают, по спирали опускаясь все ниже и быстрее в атмосферу, или падают на Землю.

Атмосферное сопротивление сильнее, когда Солнце активно. Так же, как воздух в воздушном шаре расширяется и поднимается при нагревании, атмосфера поднимается и расширяется, когда Солнце дает ей дополнительную энергию. Разреженные слои атмосферы поднимаются, а их место занимают более плотные. Поэтому спутники на орбите Земли должны изменять свое положение примерно четыре раза в год, чтобы компенсировать сопротивление атмосферы. Когда солнечная активность максимальна, положение аппарата приходится корректировать каждые 2-3 недели.

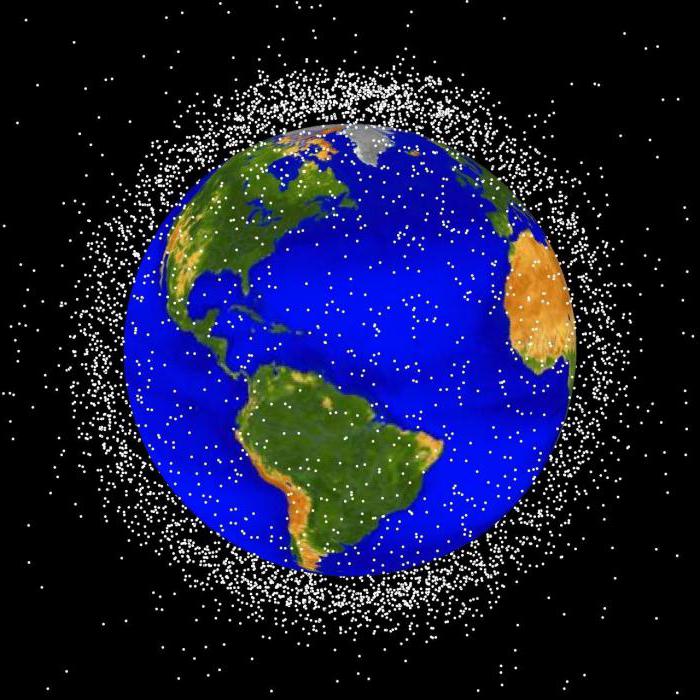
Космический мусор

Третья причина, вынуждающая менять орбиту – космический мусор. Один из коммуникационных спутников Iridium столкнулся с нефункционирующим российским космическим аппаратом. Они разбились, образовав облако мусора, состоящее из более чем 2500 частей. Каждый элемент был добавлен ​​в базу данных, которая сегодня насчитывает свыше 18000 объектов техногенного происхождения.

НАСА тщательно отслеживает все, что может оказаться на пути спутников, т. к. из-за космического мусора уже несколько раз приходилось менять орбиты.

Инженеры центра управления полетами отслеживают положение космического мусора и сателлитов, которые могут помешать движению и по мере необходимости тщательно планируют маневры уклонения. Эта же команда планирует и выполняет маневры по регулировке наклона и высоты спутника.