Как найти высоту параллелепипеда если известно основание

Геометрические фигуры. Прямоугольный параллелепипед.

Прямоугольный параллелепипед — прямой параллелепипед с прямоугольником в основании. У прямоугольного параллелепипеда каждая из шести граней является прямоугольником.

Примерами прямоугольного параллелепипеда являются спортивный зал, коробок спичек или системный блок компьютера.

Формулы прямоугольного параллелепипеда.

Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба являются равными квадратами.

Обозначим длину ребра куба как n, тогда площадь 1-ой грани:

Площадь поверхности куба:

У прямоугольного параллелепипеда есть еще одно измерение – объем параллелепипеда (обозначается как V).

Прямоугольники, которые составляют поверхность параллелепипеда, являются гранями параллелепипеда.

Прямоугольный параллелепипед определяют 3-мя измерениями:

Высота (обозначают как h) равняется длине ребра № 1.

Длина (обозначают как m) равняется длине ребра № 2.

Ширина (обозначают как n) равняется длине ребра № 3.

Площадь всей поверхности параллелепипеда обозначают как S:

В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.

Прямоугольный параллелепипед

Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

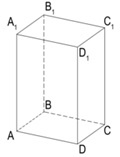
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.

Свойства прямоугольного параллелепипеда:

1. В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
2. Противоположные грани попарно равны и параллельны.
3. Все двугранные углы прямоугольного параллелепипеда – прямые.
4. Диагонали прямоугольного параллелепипеда равны.
5. Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$с$ — высота(она же боковое ребро);

$P_$ — периметр основания;

$S_$ — площадь основания;

$S_$ — площадь боковой поверхности;

$S_$ — площадь полной поверхности;

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

$S_=P_·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.

Дополнительные сведения, которые пригодятся для решения задач:

$а$ — длина стороны.

$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Объем любой пирамиды равен трети произведения основания и высоты.

В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

• $S=/$, где $h_a$ — высота, проведенная к стороне $а$.
• $S=/$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
• Формула Герона $S=√

  $, где $р$ — это полупериметр $p=/$.

• $S=p·r$, где $r$ — радиус вписанной окружности.
• $S=/$, где $R$ — радиус описанной окружности.
• Для прямоугольного треугольника $S=/$, где $а$ и $b$ — катеты прямоугольного треугольника.
• Для равностороннего треугольника $S=/$, где $а$ — длина стороны.

В основании лежит четырехугольник.

1. Прямоугольник.
   $S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб.
   $S=/$, где $d_1$ и $d_2$ — диагонали ромба.
   $S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
3. Трапеция.
   $S=/$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
4. Квадрат.
   $S=a^2$, где $а$ — сторона квадрата.

Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.

Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.

Объем пирамиды, в основании которой лежит прямоугольник

Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.

В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.

Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Измерения прямоугольного параллелепипеда и его свойства

Что такое прямоугольный параллелепипед — определение

Параллелепипед — это призма с шестью гранями, в основании которой лежит параллелограмм.

Согласно другому определению, это многогранник, состоящий из шести сторон-параллелограммов.

В математике в целом, и в геометрии в частности, выделяют несколько основных видов параллелепипеда:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

• прямоугольный;
• прямой — параллелепипед, у которого 4 боковые грани являются прямоугольниками;
• наклонный — боковые грани объемной фигуры не перпендикулярны основаниям;
• ромбоэдр — шестигранная призма, грани которой — это ромбы;
• куб — состоит из квадратных граней.

Прямоугольный параллелепипед — это шестигранная призма, каждая из сторон которой в общем случае является прямоугольником. Также это — многогранник, в основании которого лежит прямоугольник, а боковые грани перпендикулярны основанию.

Прямоугольных параллелепипедов в окружающем человека мире множество: комната, закрытая книга, системный блок компьютера, закрытая коробка для подарка, спичечный коробок и т. д.

Прямоугольный параллелепипед, как и любой другой, состоит из:

• основания;
• граней — противоположных, т. е. не имеющих общего ребра, и смежных — тех, которые имеют общее ребро;
• ребер — отрезков, соединяющих соседние вершины объемной шестигранной фигуры;
• диагоналей — отрезков, соединяющих противоположные вершины;
• диагоналей граней;
• высоты — отрезка, соединяющего верхнее и нижнее основания шестигранной призмы.

В некоторых базовых задачах просят найти количество составляющих элементов шестигранной призмы. Эти числа можно запомнить: объемная фигура состоит из 8 вершин, 12 ребер и 6 граней.

Измерениями прямоугольного параллелепипеда называют его длину, ширину и высоту.

Свойства параллелепипеда, какими обладают противолежащие грани

Вне зависимости от вида параллелепипеда, все они обладают 4 свойствами:

1. Противолежащие грани равны друг другу и попарно параллельны.
2. Все 4 диагонали шестигранника пересекаются в одной точке, которой делятся пополам. Любой отрезок, проходящий через середину диагонали, и концы которого принадлежат поверхности, также делится пополам.
3. Фигура симметрична относительно середины диагонали.
4. Квадрат длины диагонали равен сумме квадратов трех измерений.

Прямоугольный параллелепипед обладает всеми этими свойствами и несколькими специфичными, свойственными только ему.

1. Все стороны — прямоугольники.
2. Все углы, состоящие из двух граней, равны 90°.
3. Любую сторону можно принять за основание.
4. Если все ребра равны и перпендикулярны, то такой шестигранник считается кубом.

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда равен длине, умноженной на ширину и высоту.

где V — объем, a — длина, b — ширина, h — высота.

Площадь боковой поверхности равна сумме площадей боковых граней.

Площадь полной поверхности равна сумме площадей боковых граней и оснований.

Как найти диагональ и ширину прямоугольного параллелепипеда

В соответствии с одним из основных свойств параллелепипеда, квадрат длины диагонали равен сумме квадратов трех измерений. Запишем в виде формулы:

Следовательно, длина диагонали равна квадратному корню из суммы трех измерений фигуры:

Длина, ширина и высота, как правило, вычисляются через формулу объема:

Существует и второй вариант, как возможно найти одно из измерений. Если известно смежное ему измерение и диагональ общей стороны шестигранника, то можно вычислить вторую сторону через теорему Пифагора или по свойствам диагонали.