Объем параллелепипеда, построенного на векторах онлайн
Объём параллелепипеда равен смешанному произведению векторов на которых он построен:
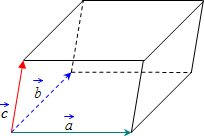
Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела – всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Задача 61425 Объём параллелепипеда, построенного на.
Условие
![]()
Объём параллелепипеда, построенного на векторах a, b, c, равен V = 12.
Площадь параллелограмма, построенного на векторах a, b, равна S = 3. Найти высоту
параллелепипеда, построенного на векторах 2a + b, a − b, a + b + 4c, которая опущена из
конца третьего вектора на грань, построенную на первых двух.
Решение
![]()
По условию:
S_(данного параллелограмма)=3 ⇒[m] |[vec × vec]|=3[/m]
Найдем векторное произведение:
Найдем смешанное произведение
V_( параллелепипеда)=S_( основания )*Н=S_( параллелограмма)*Н
Смешанное, векторное и скалярное произведение векторов
Задача:
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Найти:
Решение:
- а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA1). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.
| (AB AD AA1) | = |
|
= | 20 — 18 + 0 — 0 — 30 + 16 | = | -12 | . |
|---|
Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
VABCDA1B1C1D1=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. SABCD= |[AB AD]|.
| [AB AD] | = |
|
= | 6i — 8j — 2k | , |
|---|
Теперь найдём модуль этого вектора:
| SABCD= |[AB AD]|=√ | (36+64+4) | =2√(26). |
|---|
| [AD AA1] | = |
|
= | 9i — 16j — k | , |
|---|
SADD1A1= |[AD AA1]|=√(81+256+1)=13√2.
| h | = |
|
= |
|
= |
|
= |
|
. |
|---|
| cos(λ1) | = |
|
. |
|---|
Координаты вектора AB мы имеем, от вектор B1D надо найти. Для этого используем следующую формулу:
B1D = B1A1 + A1A + AD = — AB — AA1 + AD1 = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты. )
Сделав вычисления по этой формуле, мы найдём, что вектор B1D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B1D:
|AB|=√(16+9+0)=5, |B1D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B1D, (AB B1D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:
| cos(λ1) | = |
|
= |
|
. |
|---|
д) Что бы найти cos(λ2), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD1A1 мы можем взять вектор [AD AA1], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.
| cos(λ2) | = |
|
= |
|
. |
|---|
Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD1A1.
[spoiler title=”источники:”]
http://reshimvse.com/zadacha.php?id=61425
http://matemonline.com/primeru/zada4a-na-vektor/
[/spoiler]
Параллелепипед – это частный случай призмы, у которой основание и грани представляют собой параллелограмм.
Различают несколько разновидностей этой геометрической фигуры – прямой / прямоугольный параллелепипед, наклонный параллелепипед.
Высота параллелепипеда – это отрезок, который соединяет плоскости верхнего основания и нижнего основания параллелепипеда.
Высота перпендикулярна плоскости нижнего основания.

Для того, чтобы найти высоту параллелепипеда, можно воспользоваться традиционной формулой:
H = V / S.
H – высота параллелепипеда, V – объём параллелепипеда, S – площадь основания.
При этом объём параллелепипеда вычисляется по формуле: S = a * b * c, где a,b и c – это длины 3 измерений.
Что касается площади основания, то здесь может быть несколько случаев.
Если основание представляет собой параллелограмм, то S = a * b * sin(ab) – произведение 2 сторон на синус угла между ними.
Если мы имеем дело с прямоугольным параллелепипедом, то S = a * b – произведение 2 сторон.
Пример:
Боковое ребро наклонного параллелепипеда равно 10 см. Стороны основания равны 4 и 6 см, а угол между ними равен 30 градусов. Нужно найти высоту параллелепипеда.
1) V = 4 * 6 * 10 = 240 см3.
2) S = 4 * 6 * sin30° = 24 * 0,5 = 12 см.
3) H = V / S = 240 / 12 = 20 см.
Значит, высота параллелепипеда будет равна 20 см.
_
В случае с прямоугольным параллелепипедом всё немного проще.
Здесь высота будет совпадать с длиной грани (ребром) данной фигуры. Поэтому для нахождения высоты достаточно вычислить, чему равно боковое ребро.
Как найти высоту параллелипипеда зная длину и ширину при неизвестном обьёме
Найди верный ответ на вопрос ✅ «Как найти высоту параллелипипеда зная длину и ширину при неизвестном обьёме …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Математика » Как найти высоту параллелипипеда зная длину и ширину при неизвестном обьёме
Геометрические фигуры. Прямоугольный параллелепипед.
Прямоугольный параллелепипед — прямой параллелепипед с прямоугольником в основании. У прямоугольного параллелепипеда каждая из шести граней является прямоугольником.

Примерами прямоугольного параллелепипеда являются спортивный зал, коробок спичек или системный блок компьютера.
Формулы прямоугольного параллелепипеда.
Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба являются равными квадратами.
Обозначим длину ребра куба как n, тогда площадь 1-ой грани:
Площадь поверхности куба:
У прямоугольного параллелепипеда есть еще одно измерение – объем параллелепипеда (обозначается как V).
Прямоугольники, которые составляют поверхность параллелепипеда, являются гранями параллелепипеда.
Прямоугольный параллелепипед определяют 3-мя измерениями:
Высота (обозначают как h) равняется длине ребра № 1.
Длина (обозначают как m) равняется длине ребра № 2.
Ширина (обозначают как n) равняется длине ребра № 3.
Площадь всей поверхности параллелепипеда обозначают как S:
В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.
Прямоугольный параллелепипед
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.
Свойства прямоугольного параллелепипеда:
- В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
- Противоположные грани попарно равны и параллельны.
- Все двугранные углы прямоугольного параллелепипеда – прямые.
- Диагонали прямоугольного параллелепипеда равны.
- Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$с$ — высота(она же боковое ребро);
$P_$ — периметр основания;
$S_$ — площадь основания;
$S_$ — площадь боковой поверхности;
$S_$ — площадь полной поверхности;
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_=P_·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
Дополнительные сведения, которые пригодятся для решения задач:
$а$ — длина стороны.
$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Объем любой пирамиды равен трети произведения основания и высоты.
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
- $S=/$, где $h_a$ — высота, проведенная к стороне $а$.
- $S=/$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√
$, где $р$ — это полупериметр $p=/$.
- $S=p·r$, где $r$ — радиус вписанной окружности.
- $S=/$, где $R$ — радиус описанной окружности.
- Для прямоугольного треугольника $S=/$, где $а$ и $b$ — катеты прямоугольного треугольника.
- Для равностороннего треугольника $S=/$, где $а$ — длина стороны.
В основании лежит четырехугольник.
- Прямоугольник.
$S=a·b$, где $а$ и $b$ — смежные стороны. - Ромб.
$S=/$, где $d_1$ и $d_2$ — диагонали ромба.
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами. - Трапеция.
$S=/$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции. - Квадрат.
$S=a^2$, где $а$ — сторона квадрата.
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.
Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.
Объем пирамиды, в основании которой лежит прямоугольник
Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.
В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.
Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Измерения прямоугольного параллелепипеда и его свойства
Что такое прямоугольный параллелепипед — определение
Параллелепипед — это призма с шестью гранями, в основании которой лежит параллелограмм.
Согласно другому определению, это многогранник, состоящий из шести сторон-параллелограммов.
В математике в целом, и в геометрии в частности, выделяют несколько основных видов параллелепипеда:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- прямоугольный;
- прямой — параллелепипед, у которого 4 боковые грани являются прямоугольниками;
- наклонный — боковые грани объемной фигуры не перпендикулярны основаниям;
- ромбоэдр — шестигранная призма, грани которой — это ромбы;
- куб — состоит из квадратных граней.
Прямоугольный параллелепипед — это шестигранная призма, каждая из сторон которой в общем случае является прямоугольником. Также это — многогранник, в основании которого лежит прямоугольник, а боковые грани перпендикулярны основанию.
Прямоугольных параллелепипедов в окружающем человека мире множество: комната, закрытая книга, системный блок компьютера, закрытая коробка для подарка, спичечный коробок и т. д.
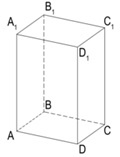
Прямоугольный параллелепипед, как и любой другой, состоит из:
- основания;
- граней — противоположных, т. е. не имеющих общего ребра, и смежных — тех, которые имеют общее ребро;
- ребер — отрезков, соединяющих соседние вершины объемной шестигранной фигуры;
- диагоналей — отрезков, соединяющих противоположные вершины;
- диагоналей граней;
- высоты — отрезка, соединяющего верхнее и нижнее основания шестигранной призмы.
В некоторых базовых задачах просят найти количество составляющих элементов шестигранной призмы. Эти числа можно запомнить: объемная фигура состоит из 8 вершин, 12 ребер и 6 граней.
Измерениями прямоугольного параллелепипеда называют его длину, ширину и высоту.
Свойства параллелепипеда, какими обладают противолежащие грани
Вне зависимости от вида параллелепипеда, все они обладают 4 свойствами:
- Противолежащие грани равны друг другу и попарно параллельны.
- Все 4 диагонали шестигранника пересекаются в одной точке, которой делятся пополам. Любой отрезок, проходящий через середину диагонали, и концы которого принадлежат поверхности, также делится пополам.
- Фигура симметрична относительно середины диагонали.
- Квадрат длины диагонали равен сумме квадратов трех измерений.
Прямоугольный параллелепипед обладает всеми этими свойствами и несколькими специфичными, свойственными только ему.
- Все стороны — прямоугольники.
- Все углы, состоящие из двух граней, равны 90°.
- Любую сторону можно принять за основание.
- Если все ребра равны и перпендикулярны, то такой шестигранник считается кубом.
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен длине, умноженной на ширину и высоту.
где V — объем, a — длина, b — ширина, h — высота.
Площадь боковой поверхности равна сумме площадей боковых граней.
Площадь полной поверхности равна сумме площадей боковых граней и оснований.
Как найти диагональ и ширину прямоугольного параллелепипеда
В соответствии с одним из основных свойств параллелепипеда, квадрат длины диагонали равен сумме квадратов трех измерений. Запишем в виде формулы:
Следовательно, длина диагонали равна квадратному корню из суммы трех измерений фигуры:
Длина, ширина и высота, как правило, вычисляются через формулу объема:
Существует и второй вариант, как возможно найти одно из измерений. Если известно смежное ему измерение и диагональ общей стороны шестигранника, то можно вычислить вторую сторону через теорему Пифагора или по свойствам диагонали.
