Высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны параллелограмма на прямую, содержащую противоположную сторону. Высотой параллелограмма также называют длину этого перпендикуляра. Для нахождения его высоты необходимо умножить синус угла на сторону.
.
Поделиться расчетом:
Вычислить высоту параллелограмма
зная длину стороны и угол
Основание параллелограмма a
Угол параллелограмма α°
Вычислить
|
В параллелограмме ABCD известно, что АВ=18, ВС=27, sin∠C=8/9. Найдите большую высоту параллелограмма.
1) Есть правило, что большая высота параллелограмма проведена к меньшей его стороне. Проведём высоту DH на сторону AB как меньшую (18<27). DH – искомая высота.
2) Получим прямоугольный треугольник ADH, в котором
Тогда из определения синуса как отношения противолежащего катета к гипотенузе получаем: DH/AD = 8/9 DH/27 = 8/9 DH = 8/9 * 27 DH = 8 * 3 DH = 24. Ответ: 24. автор вопроса выбрал этот ответ лучшим Знаете ответ? |
Примечание. Это часть урока с задачами по геометрии (раздел параллелограмм). Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме.
См. также: Свойства и площадь параллелограмма.
|
Обозначения в формулах эквивалентны обозначениям на рисунках, а именно: а – стороны, параллелограмма, параллельные друг другу b – боковые стороны параллелограмма h – высота параллелограмма d – диагональ параллелограмма S – площадь параллелограмма α – острый угол при основании параллелограмма Высота параллелограмма равна соотношению площади к основанию (Формула 1) Высота параллелограмма равна произведению боковой стороны на синус угла при основании (Формула 2) Соотношение оснований параллелограмма равно обратно пропорциональному соотношению высот, опущенных на соответствующие стороны (Формула 3) Высоты параллелограмма, опущенные из одной вершины, образуют угол, равный углу параллелограмма при соседней вершине (Рисунок 2) Высота параллелограмма равна, корню из разности квадрата боковой стороны и квадрата длины отрезка, образующего прямоугольный треугольник, другими сторонами которого являются боковая сторона и высота (Формула 4) Высота параллелограмма равна корню из разности квадрата диагонали, из которой опущена высота и квадрата длины отрезка между точкой, из которой проведена диагональ и точкой пересечения высоты и основания (Формула 5) |
Позначення у формулах еквівалентні позначенням на малюнках, а саме: а – сторони, паралелограма, паралельні один одному b – бічні сторони паралелограма h – висота паралелограма d – дiагональ паралелограма S – площа паралелограма α – гострий кут при основі паралелограма Висота паралелограма дорівнює співвідношенню площі до підстави (Формула 1) Висота паралелограма дорівнює твору бічної сторони на синус кута при його основі (Формула 2) Співвідношення підстав паралелограма дорівнює обернено пропорційному співвідношенню висот, опущених на відповідні сторони (Формула 3) Висоти паралелограма, опущені з однієї вершини, утворюють кут, рівний куту паралелограма при сусідній вершині (Малюнок 2) Висота паралелограма рівна, корню з різниці квадрата бічної сторони і квадрата довжини відрізка, створюючого прямокутний трикутник, іншими сторонами якого є бічна сторона і висота (Формула 4) Висота паралелограма дорівнює корню з різниці квадрата діагоналі, з якої опущена висота і квадрата довжини відрізка між точкою, з якої проведена діагональ і точкою пересічення висоти і основання (Формула 5) |
Решение.
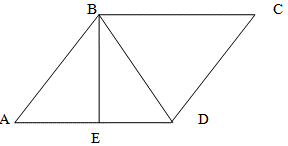
Поскольку, по условию задачи, AE=ED, то треугольники ABE и DBE равны между собой (по первому признаку равенства треугольников: равны две стороны и угол между ними, AE=ED и BE – общая сторона, а BE образует с AD угол 90 градусов). Таким образом, угол ADB равен 30 градусам. Соответственно, угол DBC также равен 30 градусам как внутренние накрест лежащие при параллельных прямых BC и AD.
Из прямоугольного треугольника ABE определим, что угол ABE равен 180 – 90 – 30 = 60 градусов. Откуда (из равенства треугольников ABE и DBE) угол EBD также равен 60 градусов. Таким образом, диагональ образует со вторым основанием угол ABD = 60 + 60 = 120 градусов. BDC = ABD = 120 градусов как внутренние накрест лежащие.
Найдем длину диагонали.
BE / BD = cos ∠EBD
BE / BD = cos 60
Подставим значение косинуса 60 градусов и получим:
BE / BD = 1/2
По условию задачи BE = 5 см, откуда
5 / BD = 1/2
BD = 10
Ответ: длина диагонали параллелограмма равна 10 см, углы, которые образует диагональ с основаниями равны 30 и 120 градусов.
 Главная
Главная  Учёба
Учёба  Вычислить высоту параллелограмма зная длину стороны и угол
Вычислить высоту параллелограмма зная длину стороны и угол
Вычислить высоту параллелограмма зная длину стороны и угол
Вам нужно указать основание параллелограмма (a) и угол параллелограмма (α).
Формула расчёта высоты параллелограмма зная длину стороны и угол: h=a*sin(α).
Умножаем сторону на угол в градусах.

| Основание параллелограмма (a) | ||
| Угол параллелограмма (градусы) (α) |
Найти длину стороны параллелограмма зная диагональ и сторону
Периметр параллелограмма
Площадь параллелограмма
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
Оставить комментарий
Заполните все поля.
Ваше имя:
| Оценка |

СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Задания
Версия для печати и копирования в MS Word
Задания Д15 № 27436 

В параллелограмме ABCD
Найдите большую высоту параллелограмма.
Спрятать решение
Решение.
выразим высоты параллелограмма через :
Однозначно, что
Ответ: 18.
Аналоги к заданию № 27436: 44407 44409 44411 … Все
Спрятать решение
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023


