Всего: 104 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Тип 17 № 65
i
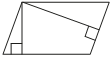
Найдите площадь параллелограмма, изображённого на рисунке.
Тип 17 № 91
i
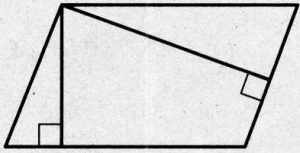
Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
Какие из следующих утверждений верны?
1) Если площади фигур равны, то равны и сами фигуры.
2) Площадь трапеции равна произведению суммы оснований на высоту.
3) Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.
4) Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то площадь этого параллелограмма равна 10.
Если утверждений несколько, запишите их номера в порядке возрастания.
На клетчатой бумаге с размером клетки 1см × 1см изображён параллелограмм. Найдите длину его большей высоты. Ответ дайте в сантиметрах.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(5 вар)
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.5)
Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар.)
В трапеции проведен отрезок, параллельный основаниям и делящий ее на две трапеции одинаковой площади. Найдите длину этого отрезка, если основания трапеции равны см и
см.
Источник: ГИА-2012. Математика. Диагностическая работа №2 (2 вар.)
Найдите площадь параллелограмма, изображённого на рисунке.
В параллелограмме ABCD проведены высоты BH и BE к сторонам AD и CD соответственно, при этом BH = BE. Докажите, что ABCD — ромб.
Найдите площадь параллелограмма, изображённого на рисунке.
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Площадь трапеции равна произведению средней линии на высоту.
Если утверждений несколько, запишите их номера в порядке возрастания.
Источник: Банк заданий ФИПИ
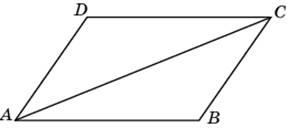
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
Источник: Банк заданий ФИПИ
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOB.
Источник: Банк заданий ФИПИ
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
Источник: Банк заданий ФИПИ
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKB.
Источник: Банк заданий ФИПИ
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника COD.
Источник: Банк заданий ФИПИ
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CMD.
Источник: Банк заданий ФИПИ
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BMC.
Источник: Банк заданий ФИПИ
Всего: 104 1–20 | 21–40 | 41–60 | 61–80 …
|
Площадь параллелограмма S можно вычислить по формуле S=ah, где a – сторона параллелограмма, h — высота, проведенная к этой стороне. Пользуясь этой формулой, найдите высоту h, если площадь параллелограмма равна 18, а сторона а равна 3,6. Известно, что площадь S параллелограмма равна произведению длины а стороны параллелограмма на длину h его высоты, проведённой к данной стороне параллелограмма. Следовательно, длина высоты h равна частному от деления площади S на длину а: h = S/a = 18/3,6 = 5. Ответ: h = 5. автор вопроса выбрал этот ответ лучшим Знаете ответ? |

Один из видов заданий из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, которые могут вам попасться на реальном экзамене в этом году. Это задание с кратким ответом. Обратите внимание, что нужно записать только одно из найденных значений – либо большее, либо меньшее.
В данной задаче достаточно воспользоваться первой формулой нахождения площади параллелограмма:
S=ah, где а – сторона параллелограмма, а h – высота, опущенная к этой стороне,
и выразить отсюда высоту.
Реальные задания по геометрии из банка ФИПИ
Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найдите его высоты. В ответе укажите бо́льшую высоту.
Решение:
Площадь параллелограмма
S=ah, где а – сторона параллелограмма, а h – высота, опущенная к этой стороне.
h=S/a
Тогда первая высота:
h1=40/5=8;
вторая высота:
h2=40/10=4.Ответ: 8
925604
Площадь параллелограмма равна 36, а две его стороны равны 6 и 12. Найдите его высоты. В ответе укажите бо́льшую высоту.
Решение:
Площадь параллелограмма
S=ah, где а – сторона параллелограмма, а h – высота, опущенная к этой стороне.
h=S/a
Тогда первая высота:
h1=36/6=6;
вторая высота:
h2=36/12=3.Ответ: 6
0D236F
Площадь параллелограмма равна 32, а две его стороны равны 8 и 16. Найдите его высоты. В ответе укажите бо́льшую высоту.
Решение:
Площадь параллелограмма
S=ah, где а – сторона параллелограмма, а h – высота, опущенная к этой стороне.
h=S/a
Тогда первая высота:
h1=32/8=4;
вторая высота:
h2=32/16=2.Ответ: 4
8DCDA9
Площадь параллелограмма равна 45, а две его стороны равны 5 и 15. Найдите его высоты. В ответе укажите бо́льшую высоту.
Решение:
Площадь параллелограмма
S=ah, где а – сторона параллелограмма, а h – высота, опущенная к этой стороне.
h=S/a
Тогда первая высота:
h1=45/5=9;
вторая высота:
h2=45/15=3.Ответ: 9
214369
Площадь параллелограмма равна 30, а две его стороны равны 6 и 10. Найдите его высоты. В ответе укажите бо́льшую высоту.
Решение:
Площадь параллелограмма
S=ah, где а – сторона параллелограмма, а h – высота, опущенная к этой стороне.
h=S/a
Тогда первая высота:
h1=30/6=5;
вторая высота:
h2=30/10=3.Ответ: 5
9E760F
Площадь параллелограмма равна 28, а две его стороны равны 14 и 7. Найдите его высоты. В ответе укажите бо́льшую высоту.
Решение:
Площадь параллелограмма
S=ah, где а – сторона параллелограмма, а h – высота, опущенная к этой стороне.
h=S/a
Тогда первая высота:
h1=28/14=2;
вторая высота:
h2=28/7=4.Ответ: 4
DE5CEA
Площадь параллелограмма равна 48, а две его стороны равны 8 и 16. Найдите его высоты. В ответе укажите меньшую высоту.
Решение:
Площадь параллелограмма
S=ah, где а – сторона параллелограмма, а h – высота, опущенная к этой стороне.
h=S/a
Тогда первая высота:
h1=48/8=6;
вторая высота:
h2=48/16=3.Ответ: 3
FE1E2B
Площадь параллелограмма равна 54, а две его стороны равны 9 и 18. Найдите его высоты. В ответе укажите меньшую высоту.
Решение:
Площадь параллелограмма
S=ah, где а – сторона параллелограмма, а h – высота, опущенная к этой стороне.
h=S/a
Тогда первая высота:
h1=54/9=6;
вторая высота:
h2=54/18=3.Ответ: 3
74F13B
Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите бо́льшую высоту.
Решение:
Площадь параллелограмма
S=ah, где а – сторона параллелограмма, а h – высота, опущенная к этой стороне.
h=S/a
Тогда первая высота:
h1=60/4=15;
вторая высота:
h2=60/20=3.Ответ: 15
336633
Площадь параллелограмма равна 56, а две его стороны равны 7 и 28. Найдите его высоты. В ответе укажите меньшую высоту.
Решение:
Площадь параллелограмма
S=ah, где а – сторона параллелограмма, а h – высота, опущенная к этой стороне.
h=S/a
Тогда первая высота:
h1=56/7=8;
вторая высота:
h2=56/28=2.Ответ: 2
EA5060
И небольшой лайфхак, позволяющий сэкономить время. Если нужно узнать бо́льшую высоту, то делим только на меньшую сторону; если меньшую высоту – делим на большую сторону, а вторую считать не имеет практического смысла.
Площадь параллелограмма равна 48, а две его стороны равны 8 и 16. Найдите его высоты. В ответе укажите меньшую высоту.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
S▱ = 48
a1 = 8
a2 = 16
h1 – ?
h2 – ?
Площадь параллелограмма находится по формуле:
S▱ = a·h
Найдём высоты данного параллелограмма:
48 = 8·h1
h_{1}=frac{48}{8}=6
48 = 16·h2
h_{2}=frac{48}{16}=3
Меньшая высота равна 3.
Ответ: 3.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.3 / 5. Количество оценок: 18
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
РЕШЕНИЕ ЗАДАНИЙ ОГЭ по теме «ПАРАЛЛЕЛОГРАММ»
Памятка.
Четырехугольник, у которого противоположные стороны параллельны, называется параллелограммом.
Свойства:
-
В параллелограмме противоположные стороны равны.
-
В параллелограмме противоположные углы равны.
-
В параллелограмме сумма углов, прилегающих к одной стороне, равна 180°.
-
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
-
Диагональ параллелограмма делят его на два равных треугольника.
Признаки:
-
Если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам, то этот четырехугольник параллелограмм.
-
Если в четырехугольнике две противоположные стороны параллельны и равны, то этот четырехугольник параллелограмм.
-
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник параллелограмм.
-
Если в четырехугольнике противоположные углы попарно равны, то этот четырехугольник параллелограмм.
Свойство диагоналей параллелограмма:
-
Диагонали параллелограмма пересекаются и в точке пересечения делятся пополам.
Свойство противоположных сторон и углов параллелограмма:
-
У параллелограмма противоположные стороны и углы равны.
Это интересно:
-
Если провести биссектрисы двух противоположных углов параллелограмма, то они будут параллельны или совпадут.
-
Если провести биссектрисы двух углов, прилегающих к одной стороне параллелограмма, то они будут перпендикулярны.
Площадь параллелограмма.
S = ah, S = 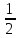
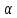
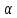
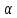
В параллелограмме можно из одного угла провести 2 высоты.
Меньшая высота проведена к большей стороне.
Большая – к меньшей.
Если в четырехугольник вписана окружность, то суммы противоположных сторон равны.
АD + BC = AB + CD
РЕШЕНИЕ ЗАДАЧ.
1.Диагональ параллелограмма образует с двумя его сторонами углы 26° и 34°. Найдите больший угол параллелограмма. Ответ дайте в градусах.
Решение.


Ответ. 120
2.Диагональ параллелограмма образует с двумя его сторонами углы 33° и 11°. Найдите больший угол параллелограмма. Ответ дайте в градусах.
3. Диагональ параллелограмма образует с двумя его сторонами углы 24° и 47° . Найдите больший угол параллелограмма. Ответ дайте в градусах.
4.В параллелограмме ABCD диагональ АС в 2 раза больше стороны АВ и 
Решение. Пусть CD = x, тогда и ОС = х, ОС = СD, 

5. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=1°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
6. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=166°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
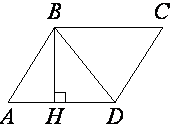
7. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Решение.AD = 1 + 28 = 29. BH = 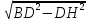
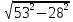
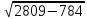
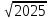
S = AH•BH, S = 29•45 = 1305.
8. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
9. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=8 и HD=40. Диагональ параллелограмма BD равна 50. Найдите площадь параллелограмма.
10. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла Aобразует со стороной BC угол, равный 15°. Ответ дайте в градусах.
Решение. ВС 








11. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 33°. Ответ дайте в градусах.
12. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
13. Найдите площадь параллелограмма, изображённого на рисунке.
14.
15. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма. Ответ дайте в градусах.
16. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
17. На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
1. 2. 3.
18. Площадь параллелограмма ABCD равна 24. ТочкаE – середина стороны CD. Найдите площадь трапеции ABED.
Решение. Пусть DE = x, тогда АВ = 2х, Sтрапеции = •h =
Sпаралл. = CD•h = 2x•h = 24, xh = 12, тогдаSтр= = 18
19.Площадь параллелограмма равна 189. Точка
— середина стороны
. Найдите площадь трапеции
.
20. Площадь параллелограмма равна 123. Точка
— середина стороны
. Найдите площадь трапеции
.
ОТВЕТЫ.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Ответ |
120 |
136 |
109 |
38 |
89,5 |
7 |
1305 |
1024 |
1440 |
30 |
|
№ |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Ответ |
66 |
82 |
120 |
20 |
105 |
45 |
1) 28 2) 10 3) 20 |
18 |
141,75 |
92,25 |
II часть.
1.Биссектриса угла параллелограмма
пересекает сторону
в точке
. Найдите периметр параллелограмма, если
,
.
Решение.
АК – биссектриса, поэтому



2.Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=5, CK=14. Ответ. 38
Решите самостоятельно:
1. Диагональ параллелограмма образует с двумя его сторонами углы 52° и 10°. Найдите больший угол параллелограмма. Ответ дайте в градусах.
2. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=173°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
3. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=7 и HD=24. Диагональ параллелограмма BD равна 51. Найдите площадь параллелограмма.
4. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 40°. Ответ дайте в градусах.
5. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
II часть.
1. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=8, CK=13.