Задания
Версия для печати и копирования в MS Word
Тип 18 № 311400 

i
На клетчатой бумаге с размером клетки 1см × 1см изображён параллелограмм. Найдите длину его большей высоты. Ответ дайте в сантиметрах.
Спрятать решение
Решение.
Большей будет высота, проведённая к меньшей стороне. По рисунку видно, что длина большей высоты параллелограмма равна 5 см.
Ответ: 5.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(5 вар)
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Спрятать решение
·
Помощь
Рубрика Задание 3, Решаем ЕГЭ по математике Комментарии (0)
Задание. На клетчатой бумаге с размером клетки 1 на 1 изображен параллелограмм. Найдите длину его большей высоты.

Решение:
Проведем высоты параллелограмма (см. рисунок).
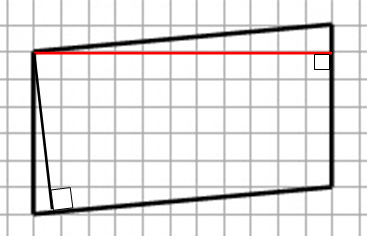
Большей высотой является высота красного цвета. Длину этой высоты легко подсчитать по клеточкам, ее длина будет равна 11.
Ответ: 11
Понравилось? Нажмите
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6c6314d09a5f7b7f • Your IP : 178.45.231.185 • Performance & security by Cloudflare
На клетчатой бумаге с размером клетки 1×1 изображен параллелограмм. Найдите его площадь.
Задача #1 (номер задачи на fipi.ru — 71E23E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Площадь параллелограмма вычисляется по формуле:
где a — основание параллелограмма, h — высота параллелограмма.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 7, а высота: h = 4.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 28 ед. кв.
Задача #2 (номер задачи на fipi.ru — 3BD9B6). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5. Из рисунка также находим высоту параллелограмма: h = 3.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 15 ед. кв.
Задача #3 (номер задачи на fipi.ru — 5C5046). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5. Из рисунка также находим высоту параллелограмма: h = 4.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 20 ед. кв.
Задача #4 (номер задачи на fipi.ru — 566A4E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 3.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 18 ед. кв.
Задача #5 (номер задачи на fipi.ru — 0275CC). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 6.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 36 ед. кв.
Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике
Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.
Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.
Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.
Больше полезных формул — в нашем ЕГЭ-Справочнике.
В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.
Вычисление длин отрезков, величин углов и площадей фигур по формулам
1. На клетчатой бумаге с размером клетки  изображена трапеция. Найдите длину средней линии этой трапеции.
изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:
2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на
4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки  Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:
 , где и — диагонали.
, где и — диагонали.
Получим: 
5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки  Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Нахождение площадей многоугольников сложной формы
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.
6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.
Согласно формуле Пика, площадь многоугольника равна В+Г/2-1
где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.
Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.
Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.
Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 – 1 = 10,5.
Выбирайте — какой способ вам больше нравится.
8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.
Площадь каждого из больших треугольников равна
Площадь каждого из маленьких треугольников равна
Тогда площадь четырехугольника
9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 

На рисунке изображен ромб с вырезанным из него квадратом.
Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.
Площадь фигуры равна 36 – 4 = 32.
Площадь круга, длина окружности, площадь части круга
Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.
Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.
10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.
Значит, нам надо умножить площадь круга на . Получим:
12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 – 9 = 7.
Задачи на координатной плоскости
13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда
14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/zadanie-3-zadachi-na-kletchatoj-bumage-ili-koordinatnoj-ploskosti/
[/spoiler]
Задание №3 из ЕГЭ прошлых лет
Задача № 1
Найдите высоту треугольника ABC, опущенную на сторону BC, если стороны квадратных клеток равны √5 (Рис. 1)
Рис. 1
Решение
В этой задаче важным моментом является то, что размер квадратных клеток равен не «1», а √5. В остальном алгоритм решения таких задач идентичен другим подобным.
Проанализируем рисунок (Рис. 1). На рисунке изображен равнобедренный треугольник: AB = AC, поэтому высота, проведенная к основанию ВС, является медианой. В то же время она является диагональю прямоугольника со сторонами 1×2 клетки (Рис. 2).

Рис. 2
По теореме Пифагора, с учетом нестандартных размеров клетки, получим:

Ответ: 5.
Задача № 2
На клетчатой бумаге с размером клетки 1 на 1 изображён параллелограмм (Рис. 3). Найдите длину его большей высоты.
Рис. 3
Решение
Сделаем дополнительные построения (Рис. 4). Проведем высоту DH из вершины D. Данная высота будет наибольшей. По рисунку найдем ее длину.

Рис. 4
Длина DH равна 4.
Ответ: 4.
Задача № 3
На клетчатой бумаге с размером клетки 1см на 1см изображена трапеция (Рис. 5). Найдите длину средней линии этой трапеции.
Рис. 5
Решение
Построим среднюю линию заданной трапеции (Рис. 6).

Рис. 6
Мы знаем, что средняя линия трапеции равна полусумме её оснований. Воспользуемся этой формулой и вычислим МК:

Ответ: 3.
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Рассмотрим несколько задач на данную тему.
| #1 | #2 | #3 | #4 | #5 |
Задача #1
(Номер задачи на fipi.ru — 71E23E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
![]()
Прежде чем приступать к решению задачи, вспомним теорию >>
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Площадь параллелограмма вычисляется по формуле:
где a — основание параллелограмма, h — высота параллелограмма.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 7, а высота: h = 4.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
![]()
Ответ: площадь параллелограмма равна: 28 ед. кв.
Задача #2
(Номер задачи на fipi.ru — 3BD9B6). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
![]()
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5. Из рисунка также находим высоту параллелограмма: h = 3.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
![]()
Ответ: площадь параллелограмма равна: 15 ед. кв.
Задача #3
(Номер задачи на fipi.ru — 5C5046). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
![]()
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5. Из рисунка также находим высоту параллелограмма: h = 4.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
![]()
Ответ: площадь параллелограмма равна: 20 ед. кв.
Задача #4
(Номер задачи на fipi.ru — 566A4E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
![]()
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 3.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
![]()
Ответ: площадь параллелограмма равна: 18 ед. кв.
Задача #5
(Номер задачи на fipi.ru — 0275CC). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
![]()
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 6.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
![]()
Ответ: площадь параллелограмма равна: 36 ед. кв.
