Параллелепипед – это частный случай призмы, у которой основание и грани представляют собой параллелограмм.
Различают несколько разновидностей этой геометрической фигуры – прямой / прямоугольный параллелепипед, наклонный параллелепипед.
Высота параллелепипеда – это отрезок, который соединяет плоскости верхнего основания и нижнего основания параллелепипеда.
Высота перпендикулярна плоскости нижнего основания.
Для того, чтобы найти высоту параллелепипеда, можно воспользоваться традиционной формулой:
H = V / S.
H – высота параллелепипеда, V – объём параллелепипеда, S – площадь основания.
При этом объём параллелепипеда вычисляется по формуле: S = a * b * c, где a,b и c – это длины 3 измерений.
Что касается площади основания, то здесь может быть несколько случаев.
Если основание представляет собой параллелограмм, то S = a * b * sin(ab) – произведение 2 сторон на синус угла между ними.
Если мы имеем дело с прямоугольным параллелепипедом, то S = a * b – произведение 2 сторон.
Пример:
Боковое ребро наклонного параллелепипеда равно 10 см. Стороны основания равны 4 и 6 см, а угол между ними равен 30 градусов. Нужно найти высоту параллелепипеда.
1) V = 4 * 6 * 10 = 240 см3.
2) S = 4 * 6 * sin30° = 24 * 0,5 = 12 см.
3) H = V / S = 240 / 12 = 20 см.
Значит, высота параллелепипеда будет равна 20 см.
_
В случае с прямоугольным параллелепипедом всё немного проще.
Здесь высота будет совпадать с длиной грани (ребром) данной фигуры. Поэтому для нахождения высоты достаточно вычислить, чему равно боковое ребро.
Тоня
Знаток
(279)
15 лет назад
Это шутка?Какая формула может быть у высоты?
Вот объем параллелепипеда такой: длину умножить на ширину и на высоту.
Отсюда,зная площадь,можно и высоту найти
Егор ГаанУченик (104)
5 лет назад
Объём прямоугольного параллепипеда 48 высота 8 надо найти площадь помогите пж
Aннушка
Гуру
(4523)
15 лет назад
ну да. согласная. вот формула
Объем прямого цилиндра равен произведению площади его основания на высоту.
Следствие 1. Объем прямоугольного параллелепипеда равен произведению трех его измерений, т.е. имеет место формула , V=a*b*c где a,b , c- –ребра параллелепипеда.
если высота а – то a= V/ (b*c) например v=a*b*c 24=2*3*4 2= 24/12
/ – знак разделить
Evgeniy Maklakov
Мастер
(1368)
15 лет назад
Она обсалютно прова >>>
Aннушка
Добавить в друзья
ну да. согласная. вот формула
Объем прямого цилиндра равен произведению площади его основания на высоту.
Следствие 1. Объем прямоугольного параллелепипеда равен произведению трех его измерений, т.е. имеет место формула , V=a*b*c где a,b , c- –ребра параллелепипеда.
Как найти высоту, если известна длина и ширина
В основании многих геометрических фигур лежат прямоугольники и квадраты. Наиболее распространен среди них параллелепипед. Также к ним относятся куб, пирамида и усеченная пирамида. Все эти четыре фигуры имеют параметр, называемый высотой.

Инструкция
Начертите простейшую изометрическую фигуру, называемую прямоугольным параллелепипедом. Она получила свое название по той причине, что ее гранями являются прямоугольники. Основание данного параллелепипеда также является прямоугольником, имеющим ширину a и длину b.
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту: V = S*h. Поскольку в основании параллелепипеда лежит прямоугольник, площадь этого основания равна S=a*b, где a – длина, b – ширина. Отсюда, объем равен V=a*b*h, где h – высота (причем, h = c, где c – ребро параллелепипеда). Если в задаче требуется найти высоту параллелепипеда, преобразуйте последнюю формулу следующим образом: h=V/a*b.
Существуют прямоугольные параллелепипеды, в основаниях которых лежат квадраты. Все его грани представляют собой прямоугольники, из которых квадратами являются два. Это означает, что его объем равен V=h*a^2, где h – высота параллелепипеда, a – длина квадрата, равная ширине. Соответственно, высоту данной фигуры найдите следующим образом: h=V/a^2.
У куба квадратами с одинаковыми параметрами являются все шесть граней. Формула для вычисления его объема выглядит так: V=a^3. Вычислять любую из его сторон, если известна другая, не требуется, поскольку все они равны между собой.
Все вышеперечисленные способы предполагают вычисление высоты через объем параллелепипеда. Однако существует и другой способ, позволяющий вычислить высоту при заданной ширине и длине. Им пользуются в том случае, если в условии задачи вместо объема приведена площадь. Площадь параллелепипеда равна S=2*a^2*b^2*c^2. Отсюда, c (высота параллелепипеда) равна с=sqrt(s/(2*a^2*b^2)).
Существуют и другие задачи по вычислению высоты при заданных длине и ширине. В некоторых из них фигурируют пирамиды. Если в задаче дан угол при плоскости основания пирамиды, а также ее длина и ширина, найдите высоту, используя теорему Пифагора и свойства углов.
Для того, чтобы найти высоту пирамиды, сначала определите диагональ основания. Из чертежа можно сделать вывод, что диагональ равна d=√a^2+b^2. Поскольку высота падает в центр основания, половину диагонали найдите следующим образом: d/2=√a^2+b^2/2. Высоту найдите, используя свойства тангенса: tgα=h/√a^2+b^2/2. Отсюда следует, что высота равна h=√a^2+b^2/2*tgα.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание
- – Как найти высоту длину ширину параллелепипеда?
- – Как узнать длину если есть ширина и высота?
- – Как находить длину прямоугольного параллелепипеда?
- – Как найти высоту параллелепипеда формула?
- – Как находить длину параллелепипеда?
- – Как найти высоту по объему?
- – Как найти длину и ширину если известна площадь 3 класс?
- – Как найти длину если известна ширина?
- – Как вычислить объем параллелепипеда формула?
- – Что нужно сделать чтобы найти ширину?
- – Как найти высоту прямоугольного параллелепипеда если его объём?
V = a × b × h, где а – длина, b – ширина, h – высота.
Как найти высоту длину ширину параллелепипеда?
Это означает, что его объем равен V=h*a^2, где h – высота параллелепипеда, a – длина квадрата, равная ширине. Соответственно, высоту данной фигуры найдите следующим образом: h=V/a^2.
Как узнать длину если есть ширина и высота?
То есть воспользуйтесь формулой:Д = П / Ш, где:Д – длина стороны прямоугольника, Ш – ширина прямоугольника, П – его площадь. Например, если площадь прямоугольника равна 20 см², а его ширина – 5 см, то длина его стороны будет: 20 / 5 = 4 см.
Как находить длину прямоугольного параллелепипеда?
V = a × b × h, где а – длина, b – ширина, h – высота. 2) Из формулы нахождения объёма парвллелепипеда выразим формулу нахождения длины: Объём параллелепипеда 40 м.
Как найти высоту параллелепипеда формула?
V= S*h. – основная формула, из нее можно вывести высоту. V- объем. S(осн) – Площадь основания.
Как находить длину параллелепипеда?
Длина прямоугольного параллелепипеда
a = V / (b * h). Итак, длина прямоугольного параллелепипеда равна отношению его объема к произведению ширины и высоты.
Как найти высоту по объему?
Как найти высоту комнаты зная объём и площадь
Объем делишь на площадь и получаешь высоту.
Как найти длину и ширину если известна площадь 3 класс?
как найти длину и ширину прямоугольника если известна площадь площадь поделить на длина+ширина!
Как найти длину если известна ширина?
С условия задачи известна ширина прямоугольника и его периметр. Для того, чтобы найти длину этого прямоугольника нужно из данной величины периметра вычесть две ширины прямоугольника и полученный результат разделить на два.
Как вычислить объем параллелепипеда формула?
Объем параллелепипеда равен произведению площади основания на высоту. где V – объем параллелепипеда, So – площадь основания, h – длина высоты.
Что нужно сделать чтобы найти ширину?
Ширину можно вычислить по длине, если известна еще площадь или периметр прямоугольника. Например, зная площадь и длину, можно найти ширину по формуле а = S/b. А зная периметр и длину, можно вычислить ширину по формуле a = (P – 2b) / 2.
Как найти высоту прямоугольного параллелепипеда если его объём?
Ответ или решение1
- Находим ширину параллелепипеда. Делим известное значение длины на разницу, которая равна 2. Будет: 10 / 2 = 5 см.
- Определяем площадь основания прямоугольного параллелепипеда. Умножаем его длину на ширину. Получим: 10 * 5 = 50 см2
- Находим высоту фигуры.
Интересные материалы:
Как спокойно пройти полиграф?
Как спорт влияет на мозг?
Как спорт влияет на сосуды головного мозга?
Как справиться с повышенным давлением?
Как справиться с зависимостью от алкоголя?
Как спрягать глагол хотеть?
Как спрягать глаголы увидеть?
Как спрятать чат в Телеграм?
Как стать администратором своего ПК?
Как стать партнером Твич?
Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).
Рисунок 1
Определение
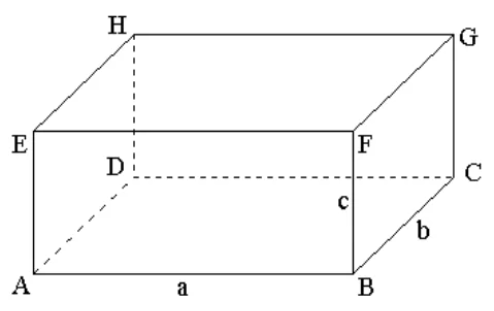
Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.
Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.
У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.
Рисунок 2
Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.
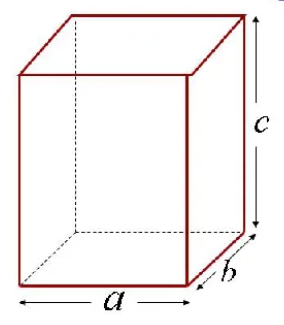
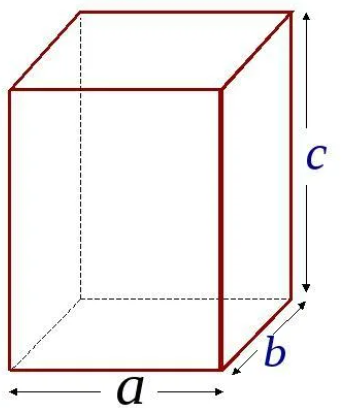
Длина, ширина, высота
Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.
Рисунок 3
Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.
Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.
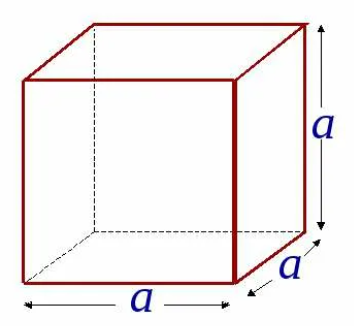
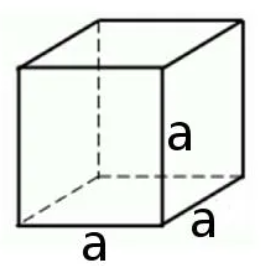
Куб
Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).
Рисунок 4
Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a2. Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a2
Объем прямоугольного параллелепипеда
Рисунок 5
С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.
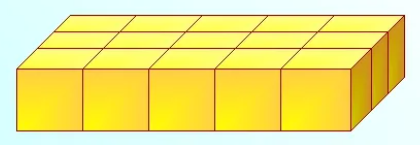
Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.
Рисунок 6
За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.
Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм3; с ребром 1 см – кубическим сантиметром (см3) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.
Формула объема прямоугольного параллелепипеда
Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.
Рисунок 7
Объем куба
Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:
V=a3
Рисунок 8
Пирамида
Рисунок 9
Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).
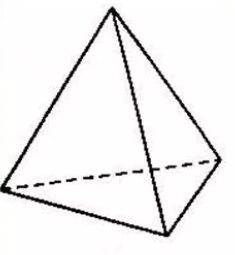
Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).
Рисунок 10
Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.
Рисунок 11
Даниил Романович | Просмотров: 1k