Помогите. Как найти высоту пирамиды если известна площадь основания и объем пирамиды
Профи
(548),
закрыт
10 лет назад
Юрий
Знаток
(499)
10 лет назад
площадь на основание надо разделить кажется так” Но мой совет геометрию можно не учить !!!она в жизни не пригодиться! сам не знаю задач за 7 класс не решу! с отличием закончил институт! Так что не парься !
Источник: Личный опыт
Станислав Греблюрве
Просветленный
(27346)
10 лет назад
Викусик! Ну, это же не задача, а упражнение! Объем пирамиды равен V =(1/3)*S*h; Отсюда: h = 3V/S. Или, еще проще: Разделите объем пирамиды на площадь и умножьте на 3, пожалуйста! Это и будет высота. Успеха Вам и “питерки”! * Примечание. Когда начинал писать ответ, других не было.. . Не ломился бы в открытую дверь!
Источник: захотелось помочь ребенку
Главная » Образование » Школа » Как найти высоту в пирамиде: треугольной, четырехугольной, правильной
Как найти высоту в пирамиде: треугольной, четырехугольной, правильной
![]()
33774 Просмотров 0

Высота основания в пирамиде – тема, на которую часто попадаются задачи на экзаменах и в старших классах. Решать такие задачи просто, если понимать принцип решения и знать формулы.
В нашей статье, вы без лишних формул и теории сможете понять, как решать задачи на нахождение высоты в пирамиде. Обратите внимание, что в разделе «формулы» отсутствуют все формулы правильной пирамиды, так как наша цель – научить решать задачи на нахождение высоты.
Содержание этой статьи:
- Теория
- Часто задаваемые вопросы
- Типичные ошибки на ЕГЭ
- Полезные советы
Теория
Это интересно: Как оформлять реферат в школе по ГОСТу + образец титульного листа 2019
Правильная пирамида
Правильная пирамида имеет в основании многоугольник, а высота проходит через центр основания. Боковые грани – равнобедренные треугольники. Напомним, что в равнобедренном треугольнике две стороны равны, следовательно, боковые ребра в правильной пирамиде тоже равны. Многоугольник в основании правильный, т.е. его стороны равны.
Для решения задач понадобится знать теоремы равнобедренного треугольника:
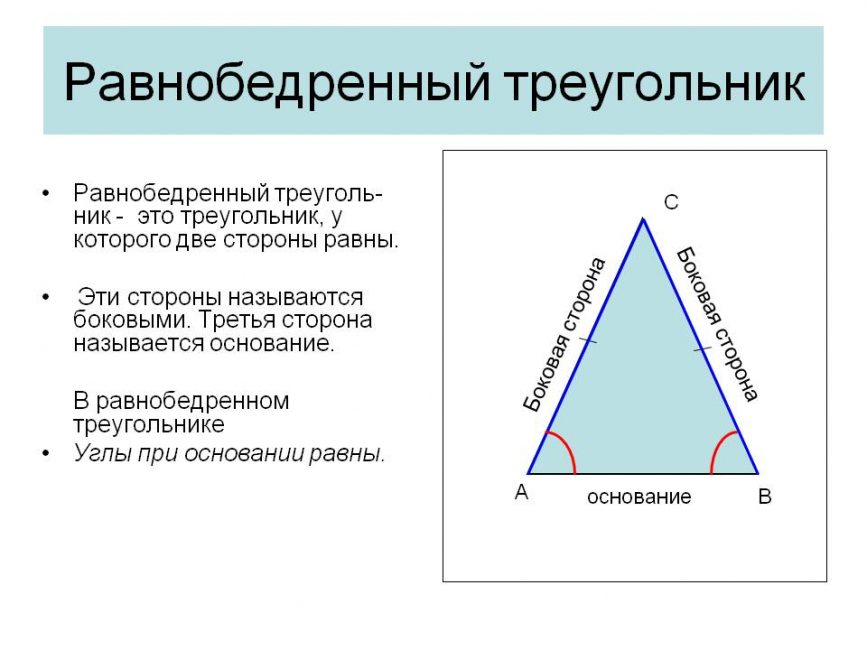
Равнобедренный треугольник
Основные свойства
1В правильную пирамиду можно вписать и описать сферу, так как при пересечении диагоналей, основание делится на равные части. Сферу нельзя вписать в любую фигуру.
2Площадь боковой поверхности – половина произведения периметра основания на апофему. Апофема есть на каждой грани, а не только на одной.
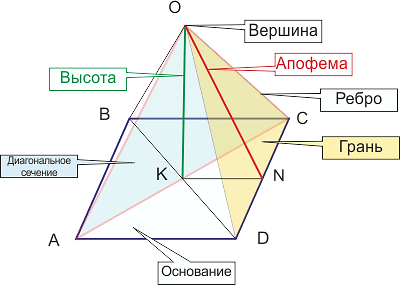
Пирамида
Четырехугольная пирамида
В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.

Четырехугольная пирамида
Треугольная пирамида
Читайте также: Как решать задачи по математике 5 класс
В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.
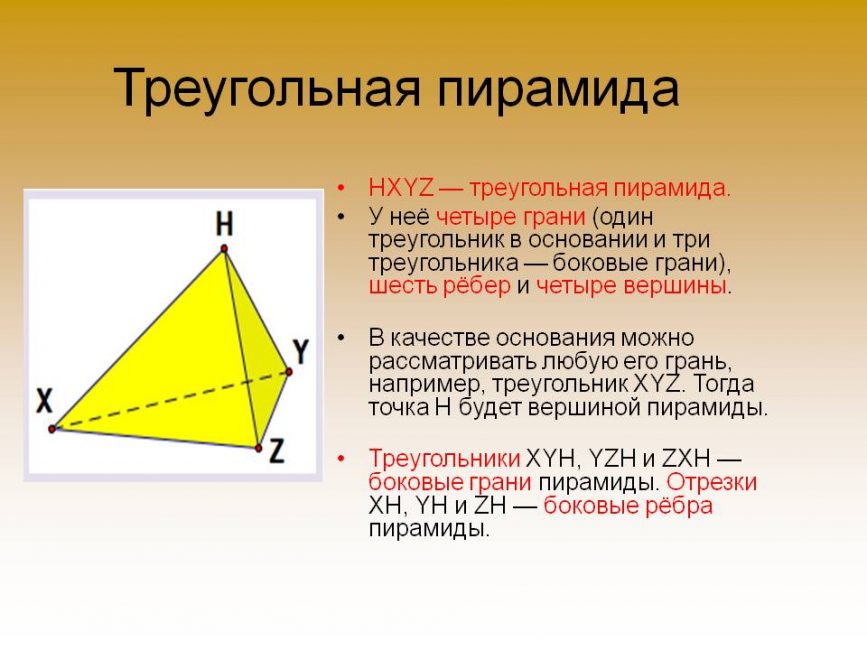
Треугольная пирамида
Необходимые знания для нахождения высоты
1Нужно понимать, что из себя представляют треугольники: свойства, формулы, определение. Большинство задач решается через треугольники (боковые грани).
2Понимать, что такое сечение и как оно влияет на геометрическую фигуру.
3Что такое правильные многоугольники: виды, свойства, формулы.
Когда теория закреплена, можно переходить к формулам.
Формулы для нахождения высоты
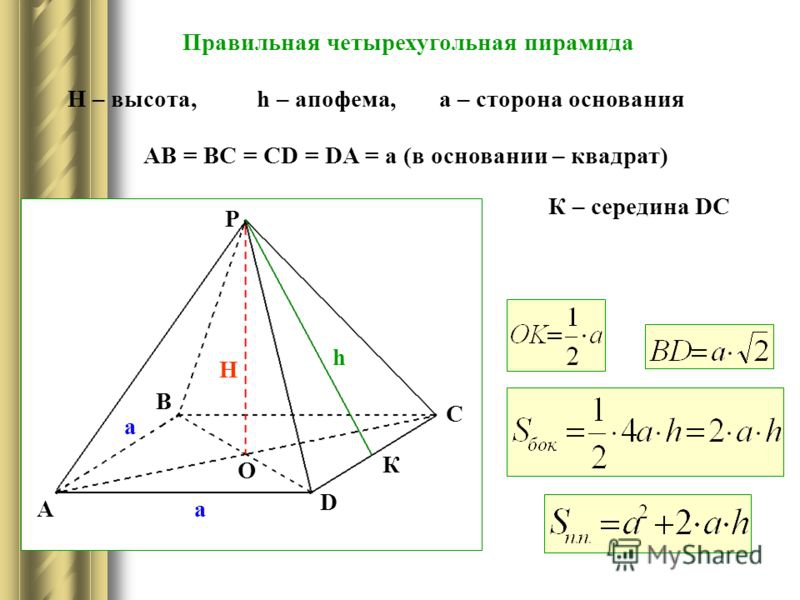
Формулы
Запомните, что маленькая буква h – это апофема, а большая H – высота.
В некоторых задачах, высоту можно найти через объем:
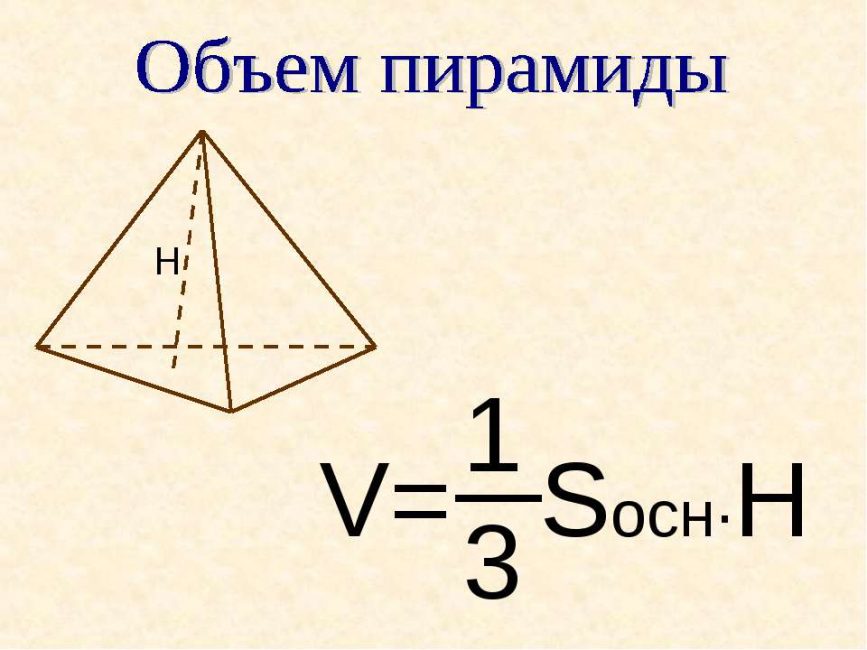
Объем пирамиды
ВИДЕО: Примеры решения задач
Нахождение высоты в правильной пирамиде
Нахождение высоты в правильной пирамиде
Ниже будут представлены текстовые решения часто встречающихся задач.
Треугольная пирамида
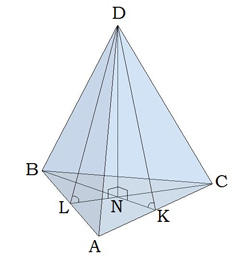
Треугольная пирамида
Задача 1
В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.
DN – высота, следовательно, объем фигуры можно выразить по формуле:
DN = 3V/S основания = 3*12/4 = 9
Ответ: 9
Задача 2
DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.
Пользуясь формулой объема, получается:
DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6
Ответ: 6
Четырехугольная пирамида
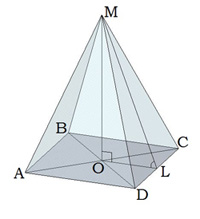
Четырехугольная пирамида
Задача 1
Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.
ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:
OL = ½*12 = 6
Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:
MO ² = √ML ² — √OL ² = √100- √36 = √64
MO = 8
Задача 2
Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.
Найдем OL
В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).
Пользуясь теоремой Пифагора, находим OL:
OL² = √OC² — √LC² = √100 – √36 = √64 = 8
Задача 3
Ищем MO
Пользуясь той же теоремой, находим высоту:
MO² = √ML² – √OL² = 100 – 64 = 36
Ответ: 36
Задача 4
Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.
Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.
Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема. Пользуясь формулами, найдем высоту.
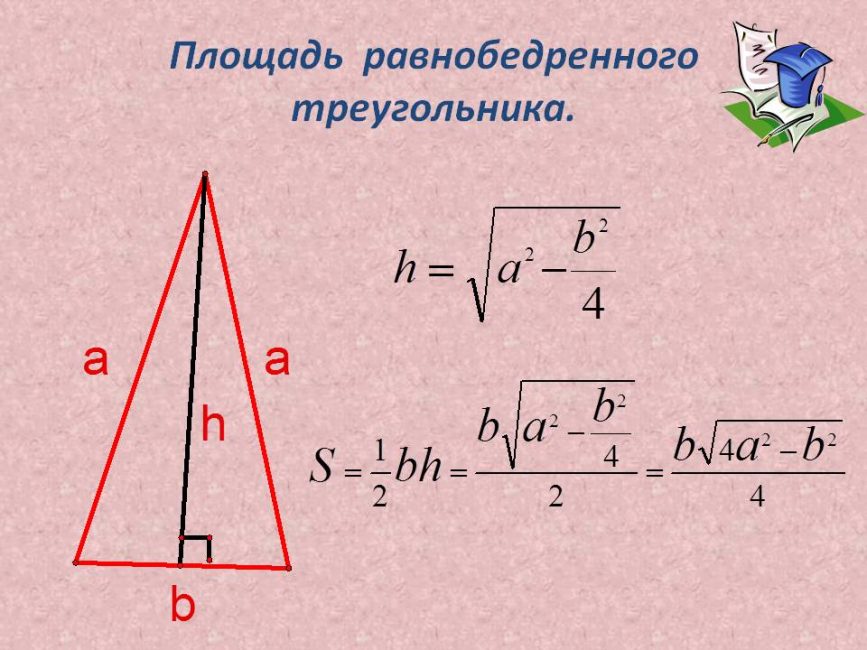
Площадь равнобедренного треугольника
36 = ½ * 4 *h
36 = 2h
H = 18
Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.
MO = ML – OL = 18 – 6 = 12
Ответ: 12
Часто задаваемые вопросы
1Как понять, что пирамида правильная, если в условии это не указано?
Часто в задании не указывают какой тип фигуры, чтобы человек сам догадался и применил нужные формулы. Понять какой тип фигуры легко – начните решение задачи с рассмотрения основания и заучивания свойств фигуры.
Зная определения и свойства, определить тип фигуры очень легко.
2Могут ли быть указаны в задании лишние данные?
Чтобы решать задачи, человек должен включать логику, а не подставлять исходные числа в знакомые формулы. С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.
3Обязательно ли оформлять высоту большой буквой H? Нужно ли выделять апофему?
Для удобства, человек может не выделять отдельно высоту, а сразу писать, например, BE (если B – вершина, а E – основание). То же с апофемой. Важно, чтобы сам человек осознавал, что это за линия и как ее использовать в решении.
4Как можно быстро изучить стереометрию?
Ключ к пониманию стереометрии – умение визуализировать объекты в пространстве. Если в дополнение к этому умению, знать формулы, свойства и теорию – задачи будут решаться быстро и безошибочно.
4Как искать высоту, если известен объем?
Если выразить высоту через формулу объема, то получится следующее:
H = (3*V)/ S;
Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²
H = 3*70/30 = 7см
Типичные ошибки на ЕГЭ
Незнание темы
Когда человек не знает, где находится апофема и что для нее есть определенные формулы, задачу может и можно решить, но тогда необходимо выполнить в 2 раза большей действий.То же обстоит с теорией – если человек не знает свойства многоугольников, то и решить задание он не сможет. Для того, чтобы понимать геометрию, не нужно обладать особенными способностями. Даже при отсутствии способностей к математике, зная теорию, вы будете понимать геометрию.
Отсутствие проверки
Хотите потерять балл на ЕГЭ? – не перепроверяйте решения. Часто, задания решаются хаотично и на листе бумаге разные решения намешаны в кучу. Когда приходит время написать ответ, человек по невнимательности либо забывает выполнить последнее действие, либо вписывает не тот ответ.Решайте задачи по действиям, проставляйте пункты и делайте проверку ответа, каким бы он ни был.
Задачи под копирку
Решая сотни аналогичных задач, человек настолько привыкает, что теряет бдительность, игнорируя многие исходные данные. Придя на экзамен, в задании может быть вопрос с подвохом и человек ошибается в теме, которую он знал идеально. Помните, к каждой задаче нужен индивидуальный подход, как бы хорошо вы в ней не разбирались.
Запись
Структурируйте решения, прописывая каждое действие и каждый полученный вывод. Это необходимо для того, чтобы не запутаться. Решая задания хаотично, можно легко записать неправильное число, не тот ответ, подставить не те числа, и задача уже решена неверно. Обидно получать низкий балл из-за невнимательности.
Подсчеты в уме
На экзамене все нервничают и переживают, а потому зарабатывают баллы ниже, чем планировалось изначально. Когда человек нервничает, уровень концентрации и внимания резко снижается. Он может упустить что-то важное, не поставить запятую или запутаться в ходе размышлений.Считая примеры в столбик, вы обезопасите себя от глупых ошибок.
Незнание структуры экзамена
Очень обидные ошибки допускают люди, пересдающие ЕГЭ через несколько лет, либо обучающиеся в экстернате. Как правило, они плохо знакомы с процедурой заполнения бланков и внесения ответов.Заполнение бланков для части А и С – различно. Внимательно посмотрите, как необходимо их заполнять, так как неправильное внесение ответа (например, запятая и число в одной клетке) будет приравниваться к ошибке и ответ будет не засчитан.Также, если вы самостоятельно готовитесь к экзамену, учитесь рассчитывать время на каждое задание.
Поспешные решения
В случае, если ответ был записан с ошибкой, его можно внести в графе ниже, заменив неправильный ответ на правильный. Однако, клетки для внесения результатов ограничены в количестве, а заданий в общей сложности 19!Несколько раз перепроверьте ответы, прежде чем внести их в бланк ответов.
Незнание степеней числа
В теореме Пифагора будут использованы не только маленькие числа (до 10). В профильной математике, могут быть крупные числа, которые тяжело посчитать в столбик.Также, степени числа могут понадобиться для других заданий. Выучите значение чисел в квадрате и кубе от 1 до 20. Помните, что на профильном экзамене, пользовать методической таблицей нельзя!
Полезные советы
- Если в задаче указан объем – ищите высоту через него.
- Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
- Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
- Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.
- Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.
6.5 Total Score
Чтобы успешно решить задачу для нахождения высоты пирамиды, достаточно знать теорию и формулы. Добавив к своим знаниям немного практики и внимательности, вы легко и быстро будете решать подобные задачи!
Если вы не согласны с рейтингом статьи, то просто поставьте свои оценки и аргументируйте их в комментариях. Ваше мнение очень важно для наших читателей. Спасибо!
Достоверность информации
8.5
Актуальность информации
7.5
ПЛЮСЫ
- Благодаря доступной информации можно легко научиться решать задачи по геометрии
МИНУСЫ
- Необходимы знания математики
Добавить отзыв
Пирамида – это многогранник, в основании которого лежит многоугольник. Все грани в свою очередь образуют треугольники, которые сходятся в одной вершине. Пирамиды бывают треугольными, четырехугольными и так далее. Для того чтобы определить, какая пирамида перед вами, достаточно посчитать количество углов в ее основании. Определение “высота пирамиды” очень часто встречается в задачах по геометрии в школьной программе. В статье попробуем рассмотреть разные способы ее нахождения.
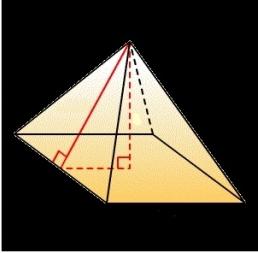
Части пирамиды
Каждая пирамида состоит из следующих элементов:
- боковые грани, которые имеют по три угла и сходятся в вершине;
- апофема представляет собой высоту, которая опускается из ее вершины;
- вершина пирамиды – это точка, которая соединяет боковые ребра, но при этом не лежит в плоскости основания;
- основание – это многоугольник, на котором не лежит вершина;
- высота пирамиды представляет собой отрезок, который пересекает вершину пирамиды и образует с ее основанием прямой угол.
Как найти высоту пирамиды, если известен ее объем
Через формулу объема пирамиды V = (S*h)/3 (в формуле V – объем, S – площадь основания, h – высота пирамиды) находим, что h = (3*V)/S. Для закрепления материала давайте сразу же решим задачу. В треугольной пирамиде площадь основания равна 50 см2, тогда как ее объем составляет 125 см3. Неизвестна высота треугольной пирамиды, которую нам и необходимо найти. Здесь все просто: вставляем данные в нашу формулу. Получаем h = (3*125)/50 = 7,5 см.
Как найти высоту пирамиды, если известна длина диагонали и ее ребра
Как мы помним, высота пирамиды образует с ее основанием прямой угол. А это значит что высота, ребро и половина диагонали вместе образуют прямоугольный треугольник. Многие, конечно же, помнят теорему Пифагора. Зная два измерения, третью величину найти будет несложно. Вспомним известную теорему a² = b² + c², где а – гипотенуза, а в нашем случае ребро пирамиды; b – первый катет или половина диагонали и с – соответственно, второй катет, или высота пирамиды. Из этой формулы c² = a² – b².
Теперь задачка: в правильной пирамиде диагональ равна 20 см, когда как длина ребра – 30 см. Необходимо найти высоту. Решаем: c² = 30² – 20² = 900-400 = 500. Отсюда с = √ 500 = около 22,4.
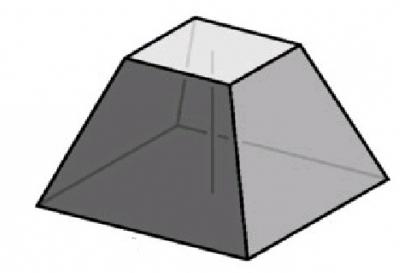
Как найти высоту усеченной пирамиды
Она представляет собой многоугольник, который имеет сечение параллельно ее основанию. Высота усеченной пирамиды – это отрезок, который соединяет два ее основания. Высоту можно найти у правильной пирамиды, если будут известны длины диагоналей обоих оснований, а также ребро пирамиды. Пусть диагональ большего основания равна d1, в то время как диагональ меньшего основания – d2, а ребро имеет длину – l. Чтобы найти высоту, можно с двух верхних противоположных точек диаграммы опустить высоты на ее основание. Мы видим, что у нас получились два прямоугольных треугольника, остается найти длины их катетов. Для этого из большей диагонали вычитаем меньшую и делим на 2. Так мы найдем один катет: а = (d1-d2)/2. После чего по теореме Пифагора нам остается лишь найти второй катет, который и является высотой пирамиды.
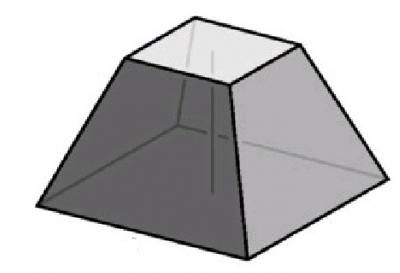
Теперь рассмотрим все это дело на практике. Перед нами задача. Усеченная пирамида имеет в основании квадрат, длина диагонали большего основания равняется 10 см, в то время как меньшего – 6 см, а ребро равняется 4 см. Требуется найти высоту. Для начала находим один катет: а = (10-6)/2 = 2 см. Один катет равен 2 см, а гипотенуза – 4 см. Получается, что второй катет или высота будет равна 16-4 = 12, то есть h = √12 = около 3,5 см.
Правильная треугольная пирамида – это пирамида, у которой в основании лежит правильный, иными
словами, равносторонний треугольник и у которой боковые стороны – это равнобедренные треугольники.
Такая объемная фигура также именуется правильным тетраэдром. Высота – это отрезок перпендикуляра,
проведенного из вершины фигуры на основание или на продолжение основания. Обозначается латинской
буквой h и на чертеже отмечается квадратом. Высота треугольной пирамиды, проведенная из вершины,
попадает на основание в центр пересечения медиан фигуры.
- Высота правильной треугольной пирамиды через обьём и
площадь основания - Высота правильной треугольной пирамиды через обьём и ребро
основания
Через объём и площадь основания
Объем любой пирамиды находится по формуле: V = 1/3h * S, где h является высотой пирамиды, а S
является площадью основания пирамиды. Из этой формулы можно получить формулу для нахождения высоты
пирамиды:
h = (V * 3) / S
Цифр после
запятой:
Результат в:
Пример. По условию дана правильная треугольная пирамида, у которой площадь
основания равна S = 18 см², а объем равен V = 90 смᶾ, нужно найти высоту фигуру. Для этого нужно
подставить в формулу все известны переменные, тогда h = 90 * 3 / 18 = 15,
значит высота равна 15 см. Так можно находить высоту и правильной, и наклонной фигуры.
Через объём и ребро основания
Найти высоту правильной треугольной пирамиды можно также через объем и ребро основания в случае,
когда неизвестна площадь основания. Вычисления в данном случае надо производить по формуле:
H = √ (V * 4 * √3 / a²)
Цифр после
запятой:
Результат в:
Пример. Дана правильная треугольная пирамида с объемом V = 90 смᶾ и длиной ребра
основания a = 5 см, нужно найти высоту этой фигуры. Подставим значения в формулу и получим: H = √ (90 * 4 * √3 / 5²) = 5 см.
Найти высоту правильной треугольной пирамиды можно также через объем и ребро основания по-другому.
Итак, V = 1/3h * S, значит h = V * 3 / S.
Поскольку площадь основания нам не известна, но известно ребро, то площадь можно выразить по
формуле: S = 1/2 * a * b * sin α, где a и b равны между собой, поскольку
пирамида по условию задачи является правильной, а sin α = sin 60°, в
равностороннем треугольнике все углы раны 60°.
Подставив формулу площади основания пирамиды через стороны треугольника и синус в исходную формулу,
получим: h = (V * 3 * 2) / (a * b * sin α).
Пример. Дана правильная треугольная пирамида с объемом V = 90 смᶾ и длиной ребра
основания a = 5 см, нужно найти высоту этой фигуры. При решении задачи сначала необходимо выполнить
все преобразования, описанные выше, а затем уже переходить к подстановке числовых значений. Это
принцип соблюдения логики при решении математических задач. В ином случае вам не поставят полный
балл за задачу, поскольку конечной формулы нет в кодификаторе. Выполнив все преобразования можно
подставлять числа, получается: h = (90 * 3 * 2) / (5 * 5 * (√3 / 2)),
преобразовываем это выражение до h = (18 * 3 * 2 * 2) / (5 * √3),
получается h = (72 * 3 * √3) / (5 * 3) = (72 * √3) / 5.
Получается для того, чтобы вычислить высоту в правильной треугольной пирамиде (тетраэдре) прежде
всего так или иначе нужно отыскать площадь основания и объем фигуры. Чтобы определить площадь
достаточно иметь данные об одном из ребер основания фигуры. Вычисление высоты пирамиды может
пригодиться при нахождении объема фигуры.
Пирамида – это многогранник, в основании которого лежит многоугольник. Все грани в свою очередь образуют треугольники, которые сходятся в одной вершине. Пирамиды бывают треугольными, четырехугольными и так далее. Для того чтобы определить, какая пирамида перед вами, достаточно посчитать количество углов в ее основании. Определение “высота пирамиды” очень часто встречается в задачах по геометрии в школьной программе. В статье попробуем рассмотреть разные способы ее нахождения.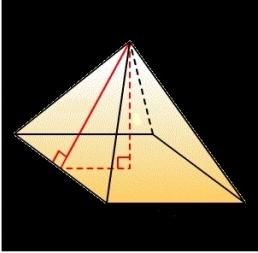
Части пирамиды
Каждая пирамида состоит из следующих элементов:
- боковые грани, которые имеют по три угла и сходятся в вершине;
- апофема представляет собой высоту, которая опускается из ее вершины;
- вершина пирамиды – это точка, которая соединяет боковые ребра, но при этом не лежит в плоскости основания;
- основание – это многоугольник, на котором не лежит вершина;
- высота пирамиды представляет собой отрезок, который пересекает вершину пирамиды и образует с ее основанием прямой угол.
Как найти высоту пирамиды, если известен ее объем
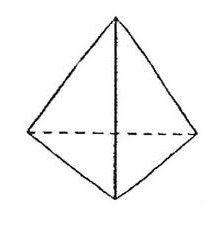
Через формулу объема пирамиды V = (S*h)/3 (в формуле V – объем, S – площадь основания, h – высота пирамиды) находим, что h = (3*V)/S. Для закрепления материала давайте сразу же решим задачу. В треугольной пирамиде площадь основания равна 50 см2, тогда как ее объем составляет 125 см3. Неизвестна высота треугольной пирамиды, которую нам и необходимо найти. Здесь все просто: вставляем данные в нашу формулу. Получаем h = (3*125)/50 = 7,5 см.
Как найти высоту пирамиды, если известна длина диагонали и ее ребра
Как мы помним, высота пирамиды образует с ее основанием прямой угол. А это значит что высота, ребро и половина диагонали вместе образуют прямоугольный треугольник. Многие, конечно же, помнят теорему Пифагора. Зная два измерения, третью величину найти будет несложно. Вспомним известную теорему a² = b² + c², где а – гипотенуза, а в нашем случае ребро пирамиды; b – первый катет или половина диагонали и с – соответственно, второй катет, или высота пирамиды. Из этой формулы c² = a² – b².
Теперь задачка: в правильной пирамиде диагональ равна 20 см, когда как длина ребра – 30 см. Необходимо найти высоту. Решаем: c² = 30² – 20² = 900-400 = 500. Отсюда с = √ 500 = около 22,4.
Как найти высоту усеченной пирамиды
Она представляет собой многоугольник, который имеет сечение параллельно ее основанию. Высота усеченной пирамиды – это отрезок, который соединяет два ее основания. Высоту можно найти у правильной пирамиды, если будут известны длины диагоналей обоих оснований, а также ребро пирамиды. Пусть диагональ большего основания равна d1, в то время как диагональ меньшего основания – d2, а ребро имеет длину – l. Чтобы найти высоту, можно с двух верхних противоположных точек диаграммы опустить высоты на ее основание. Мы видим, что у нас получились два прямоугольных треугольника, остается найти длины их катетов. Для этого из большей диагонали вычитаем меньшую и делим на 2. Так мы найдем один катет: а = (d1-d2)/2. После чего по теореме Пифагора нам остается лишь найти второй катет, который и является высотой пирамиды.
Теперь рассмотрим все это дело на практике. Перед нами задача. Усеченная пирамида имеет в основании квадрат, длина диагонали большего основания равняется 10 см, в то время как меньшего – 6 см, а ребро равняется 4 см. Требуется найти высоту. Для начала находим один катет: а = (10-6)/2 = 2 см. Один катет равен 2 см, а гипотенуза – 4 см. Получается, что второй катет или высота будет равна 16-4 = 12, то есть h = √12 = около 3,5 см.