1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
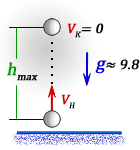
h max
– максимальная высота достигнутая телом за время t
Vк – конечная скорость тела на пике, равная нулю
Vн – начальная скорость тела
t – время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула максимальной высоты (h max):
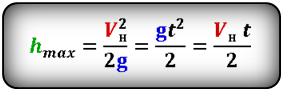
Формула времени за которое тело достигло максимальную высоту (t):
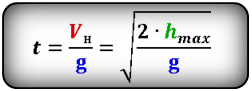
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
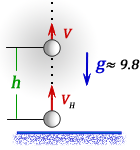
h – расстояние пройденное телом за время t
Vн – начальная скорость тела
V – скорость тела в момент времени t
t – время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула скорости тела в момент времени t (V):
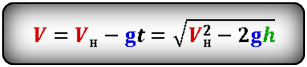
Формула начальной скорости тела (Vн):
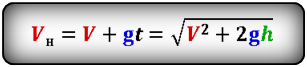
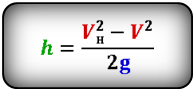
Формулы высоты тела в момент времени t (h):
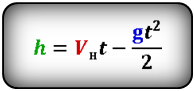
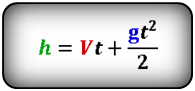
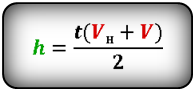
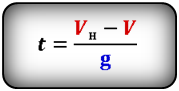
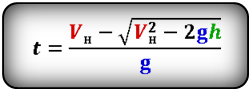
Формулы времени, за которое тело достигло высоту h (t):
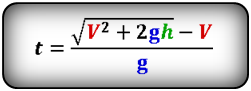
- Подробности
-
Опубликовано: 04 августа 2015
-
Обновлено: 13 августа 2021
Как искать высоту в физике?
В данном случае можем воспользоватся формулой H = (g*t^2) / 2. Где H — искомая высота g-ускорение свободного падения равное 9.8 м/c^2 t-время падения. Тогда скорость сможем рассчитать по формуле V=g*t.
Как определить высоту формула?
Первый способ найти высоту – через площадь треугольника. Площадь треугольника вычисляется по формуле: S = 1/2 ah, где (a) – сторона треугольника, h – высота, построенная к стороне (а). Из этого выражения найдите высоту: h = 2S/a.
Что такое H в физике формула?
h — высота столба жидкости, g = 9,8 м/с2.
Как найти высоту с помощью потенциальной энергии?
Потенциальную энергию тела в земном поле тяготения можно рассчитать по формуле: E=m*g*h, где m-масса тела, g-ускорение свободного падения, h-высота над уровнем, принятым за нулевой(обычно принимается уровень земной поверхности). Отсюда высота h=E/(m*g)=60/(3*10)=2 м.
Как найти высоту падения тела?
Свободное падение — прямолинейное движение с постоянным ускорением. Направим ось координат от точки начального положения тела к Земле. Применяя формулы кинематики для прямолинейного равноускоренного движения, можно записать. h=v0+gt22 h = v 0 + g t 2 2 .
Что означает буква H?
H (латиница), h — 8-я буква латинского алфавита. Η, η (эта) — 7-я буква греческого алфавита. ん, ン (Н) — знак каны. h — глухой глоттальный щелевой согласный звук в обозначении Международного фонетического алфавита.
Как найти высоту в трапеции?
Зная площадь трапеции и ее среднюю линию (или два основания, среднее арифметическое которых дает среднюю линию), можно вычислить высоту трапеции, разделив одно на другое: Более изощренным является вычисление высоты трапеции через все ее стороны.
Как найти высоту с помощью давления?
При расчете давления по формуле p = gρh надо плотность ρ выражать в килограммах на кубический метр (кг/м3), а высоту столба жидкости h — в метрах (м), g = 9,8 Н/кг, тогда давление будет выражено в паскалях (Па).
Что обозначает буква H?
В математике обозначают: буквой h — высоту какого-либо тела или фигуры; буквой H — матрицу Гильберта, полиномы Эрмита, преобразование Гильберта, преобразование Хартли, функции Ханкеля, функцию Хевисайда.
Как найти G в физике 7 класс?
очень надо Ускорение свободного падения. Ускорение свободного падения. g = 9,81 м/с2 Например, вес тела равен P = mg, где m — масса тела.
Как рассчитать потенциальную энергию поднятого над землёй тела?
Потенциальная энергия тела, поднятого над землёй, прямо пропорциональна массе m, ускорению свободного падения g и высоте нахождения тела над землёй h. Эти величины объединяются формулой: E пот = m ⋅ g ⋅ h .
Чему равна потенциальная энергия поднятого над землей тела?
Кинетическая энергия «ведет себя» противоположным образом. Следовательно, потенциальная энергия тела, поднятого на некоторую высоту над нулевым уровнем, равна работе силы тяжести, при падении тела с этой высоты до нулевого уровня.
Как найти высоту зная время падения?
h=gt22 h = g t 2 2 . Отсюда находится выражение для времени падения тела с высоты h : t=√2hg t = 2 h g .
Какую скорость развивает человек в свободном падении?
У поверхности Земли (на уровне моря) ускорение свободного падения меняется от 9,832 м/с² на полюсах до 9,78 м/с² на экваторе.
Что такое H маленькая в физике?
h — постоянная Планка. ħ — редуцированная постоянная Планка (постоянная Дирака). h — гелион. Н — напряжённость магнитного поля.
Какой буквой обозначается H?
Английский алфавит. English Alphabet
| Буква | Транскрипция | Произношение |
|---|---|---|
| G g | [dʒiː] | джи |
| H h | [eɪtʃ] | эйч |
| I i | [aɪ] | ай |
| J j | [dʒeɪ] | джей |
Чему равна h в трапеции?
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.
Путь, время, скорость
S – путь
v – скорость
t – время
Равномерное движение
x – координата
x0 – начальная координата
v – скорость
t – время
Равномерно ускоренное движение: ускорение
a – ускорение
v – скорость
v0 – начальная скорость
t – время
Равномерно ускоренное движение: скорость
v – скорость
v0 – начальная скорость
a – ускорение
t – время
Равномерно ускоренное движение: путь
s – путь
v – скорость
t – время
a – ускорение
Равномерно ускоренное движение: координата
x – координата
x0 – начальная координата
v – скорость
t – время
a – ускорение
Высота тела, брошенного вертикально вверх (вниз)
h – высота
h0 – начальная высота
v0 – начальная скорость
t – время
g – ускорение свободного падения
Скорость тела, брошенного вертикально вверх (вниз)
v – скорость
v0 – начальная скорость
g – ускорение свободного падения
t – время
Скорость, ускорение, время
v – скорость
a – ускорение
t – время
Скорость свободно падающего тела
v – скорость
g – ускорение свободного падения
t – время
Центростремительное ускорение
a – центростремительное ускорение
v – скорость
R – радиус
Угловая скорость
ω – угловая скорость
φ – угол
t – время
Равномерное круговое движение
l – длина дуги окружности
R – радиус
φ – угол
Равномерное круговое движение: линейная скорость
v – линейная скорость
R – радиус
ω – угловая скорость
Период вращения
T – период
t – время
N – число вращений
Период вращения
T – период
R – радиус
v – линейная скорость
Период вращения
T – период
ω – угловая скорость
Центростремительное ускорение
a – центростремительное ускорение
R – радиус
T – период вращения
Центростремительное ускорение
a – центростремительное ускорение
R – радиус
n – частота вращения
Частота вращения
n – частота вращения
T – период вращения
Центростремительное ускорение
a – центростремительное ускорение
ω – угловая скорость
R – радиус
Дальность броска тела, брошенного под углом к горизонту
x – координата (дальность)
v0 – начальная скорость
t – время
α – угол
Высота подъема тела, брошенного под углом к горизонту
y – координата (высота подъема )
v0 – начальная скорость
t – время
g – ускорение свободного падения
α – угол
Вертикальная скорость тела, брошенного под углом к горизонту
v_y – вертикальная скорость
v0 – начальная скорость
α – угол
g – ускорение свободного падения
t – время
Максимальная высота подъема тела, брошенного под углом к горизонту
h_макс – максимальная высота
v0 – начальная скорость
α – угол
g – ускорение свободного падения
Общее время движения тела, брошенного под углом к горизонту
t – время
v0 – начальная скорость
α – угол
g – ускорение свободного падения
Максимальная дальность броска тела, брошенного под углом к горизонту
s_макс – максимальная дальность
v0 – начальная скорость
g – ускорение свободного падения
Дальность броска тела, брошенного горизонтально
x – координата (дальность)
x0 – начальная координата
v – скорость
t – время
Высота подъема тела, брошенного горизонтально
y – координата (высота подъема)
y0 – начальная координата (высота)
g – ускорение свободного падения
t – время
Общее время движения тела, брошенного горизонтально
t_макс – максимальное время
h – высота
g – ускорение свободного падения
Если тело бросить вертикально вверх при наличии начальной скорости υ0, оно будет двигаться равнозамедленно с ускорением, равным a=-g=-9,81υc2.
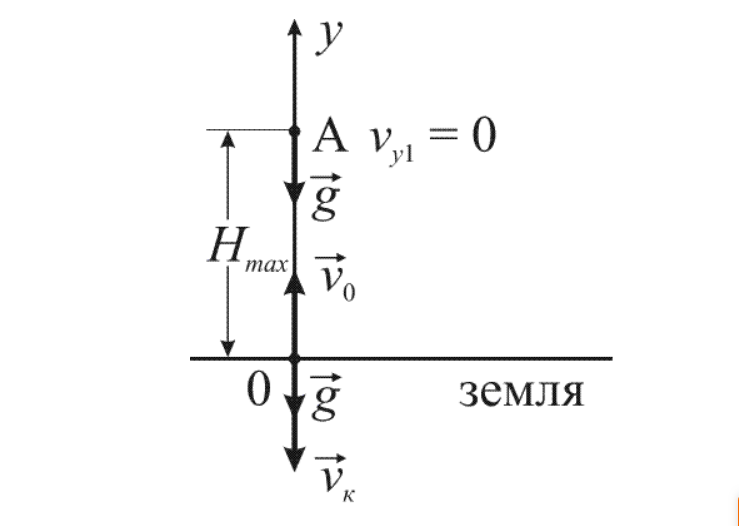
Рисунок 1
Формулы вычисления показателей движения брошенного тела
Высота подбрасывания h за время t и скорость υ через промежуток t можно определить формулами:
tmax – это время, за которое тело достигает максимальной высоты hmax=h, при υ=0, а сама высота hmax может быть определена при помощи формул:
Когда тело достигает высоты, равной hmax, то оно обладает скоростью υ=0 и ускорением g. Отсюда следует, что тело не сможет оставаться на этой высоте, поэтому перейдет в состояние свободного падения. То есть, брошенное вверх тело – это равнозамедленное движение, при котором после достижения hmax изменяются знаки перемещения на противоположные. Важно знать, какая была начальная высота движения h0. Общее время тела примет обозначение t, время свободного падения – tп, конечная скорость υк, отсюда получаем:
Если тело брошено вертикально вверх от уровня земли, то h0=0.
Время, необходимое для падения тела с высоты, куда предварительно было брошено тело, равняется времени его подъема на максимальную высоту.
Так как в высшей точке скорость равняется нулю видно:
Конечная скорость υк тела, брошенного от уровня земли вертикально вверх, равна начальной скорости υ0 по величине и противоположна по направлению, как показано на ниже приведенном графике.
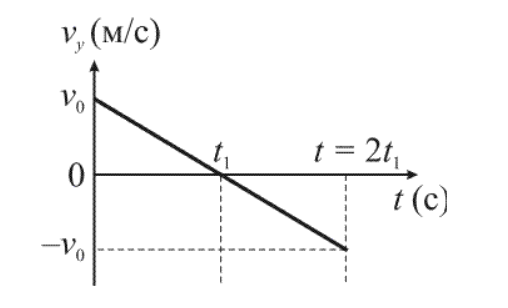
Рисунок 2
Примеры решения задач
Тело было брошено вертикально вверх с высоты 25 метров со скоростью 15 м/с. Через какой промежуток времени оно достигнет земли?
Дано: υ0=15 м/с, h0=25 м, g=9,8 м/с2.
Найти: t.
Решение
t=υ0+υ02+gh0g=15+152+9,8·259,8=3,74 с
Ответ: t=3,74 с.
Был брошен камень с высоты h=4 вертикально вверх. Его начальная скорость равняется υ0=10 м/с. Найти высоту, на которую сможет максимально подняться камень, его время полета и скорость, с которой достигнет поверхности земли, пройденный телом путь.
Дано: υ0=10 м/с, h=4 м, g=9,8 м/с2.
Найти: H, t, v2, s.
Решение
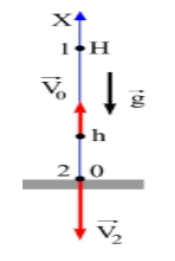
Рисунок 3
H=h0υ022g=4+1029,8=14,2 м.
t=υ0+υ02+gh0g=10+102+9,8·49,8=1,61 с.
υ2=υk=2gH=2·9,8·14,2=16,68 м/с.
s=H-h0+H=2H-h0=2·14,2=24,4 м.
Ответ: H=14,2 м; t=1,61 с; v2=16,68 м/с; s=24,4 м.
Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением
a = -g.
Перемещение тела за время t представляет собой высоту подъема h.
Для этого движения справедливы формулы:
Если:
u0 — начальная скорость движения тела ,
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота на которую поднимется тело за время t,
t — время,
То, движение тела, брошенного вертикально вверх описывается следующими формулами:
Высота подъема тела за некоторое время, зная конечную скорость
[ h = frac{u_0 + u}{2} t ]
Высота подъема тела за некоторое время, зная ускорение свободного падения
[ h = u_0 t – frac{g t^2}{2} ]
Скорость тела через некоторое время, зная ускорение свободного падения
[ u = u_0 – gt ]
Скорость тела на некоторой высоте, зная ускорение свободного падения
[ u = sqrt{ u_0^2 – 2gh} ]
Максимальная высота подъема тела, зная первоначальную скорость и ускорение свободного падения
Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в ноль. Поднявшись на максимальную высоту тело начинает свободное падение вниз.
[ h_{max} = frac{u_0^2}{2g} ]
Время подъема на максимальную высоту подъема тела, зная первоначальную скорость и ускорение свободного падения
[ t_{hmax} = frac{u_0}{g} ]
Примечание к статье: Движение тела, брошенного вертикально вверх
- Сопротивление воздуха в данных формулах не учитывается.
- Ускорение свободного падения имеет приведенное значение (9.81 (м/с²)) вблизи земной поверхности. Значение g на других расстояниях от поверхности Земли изменяется!
Движение тела, брошенного вертикально вверх |
стр. 409 |
|---|
