Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.
Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал.
Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Выберите каким образом задается пирамида (тетраэдр):
Введите значения векторов: Введите координаты вершин пирамиды:
Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Ввод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах
- Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.
Теория. Объем пирамиды (объем тетраэдра) построенной на векторах

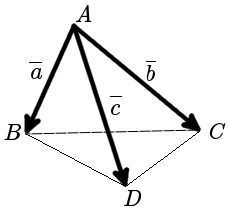
Определение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Как найти высоту пирамиды по векторам
Инструкция . Для решения подобных задач в онлайн режиме заполните координаты вершин, нажмите Далее . см. также по координатам треугольника найти.
- Решение онлайн
- Видеоинструкция
- Оформление Word
Пример №1 . В пирамиде SABC : треугольник ABC – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S . Сделать чертеж.
Решение: Координаты векторов находим по формуле: X = x2 – x1; Y = y2 – y1; Z = z2 – z1
Так, для вектора AB, это будут координаты: X = 0-2; Y = 3-0; Z = 0-0, или AB(-2;3;0).
AC(-2;0;1); AD(-2;2;3); BC(0;-3;1); BD(0;-1;3); CD(0;2;2) .
Длину вектора находим по формуле:
Пример №2 . В тетраэдре ABCD вычислить:
- объем тетраэдра ABCD;
- высоту тетраэдра, опущенную из вершины D на грань ABC.
A(2, 3, -2), B(3, 1, 0), C(-2, 2, 1), D(6, 1, -1)
Ответ
Проверено экспертом
Даны вершины пирамиды A(3;-2;3)B(-1;0;2)C(-3;1;-1)D(-3;-3;1) .
Находим векторы АВ, АС и АД.
Вектор АВ = (-4; 2; -1 ), модуль равен √(16+4+1) = √21 ≈ 4,58258.
Определяем векторное произведение АВ х АС.
-6 3 -4 | -6 3 = -8i + 6j – 12k – 16j + 3i + 12k = -5i – 10j = (-5; -10; 0).
Далее находим смешанное произведение (АВ х АС) х АД.
(АВ х АС) = (-5; -10; 0),
(АВ х АС) х АД = 30 + 10 + 0 = 40.
Объем пирамиды равен (1/6) этого произведения:
V = (1/6)*40 = (20/3) куб.ед.
Высота h пирамиды ABCD, опущенная из вершины D на плоскость основания ABC, равна: h = 3V/S(ABC).
Площадь основания АВС равна половине модуля векторного произведения АВ х АС.
S(ABC) = (1/2)*√((-5)² + (-10)² + 0²) = (1/2)√(25 + 100) = (5/2)√5 кв.ед.
h = (3*20/3)/((5/2)√5) = 8/√5 = 8√5/5 ≈ 3,5777.
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
A ( ; ; ), B ( ; ; ),
C ( ; ; ), D ( ; ; )
Примечание: дробные числа записывайте
через точку, а не запятую.
Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
Онлайн калькулятор для решения задач и работы с векторами. Зная точки вектора или координаты начала и конца вектора, векторный калькулятор использует данные по всем разделам векторов и находит не только координаты самого вектора, его направляющие косинусы и результаты сложения, вычитания и умножения, но и доказывает ортогональность или коллинеарность двух векторов, а также
угол между векторами, длину или модуль векторов, проекцию векторов, векторное произведение векторов, площадь параллелограмма и площадь треугольника построенного на векторах. Для отображение деталей расчетов активируйте формулы на панели калькулятора.
| AC | 7 | 8 | 9 | ← |
| C | 4 | 5 | 6 | ÷ |
| % | 1 | 2 | 3 | × |
| xy | . | 0 | = | – |
| x2 | √ | ( | ) | + |
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Операции над векторами: онлайн-калькуляторы
На нашем сайте представлен полный набор калькуляторов векторов онлайн, с помощью которых вы сможете получить подробное и точное решение необходимой геометрической задачи.
Чтобы найти вектор онлайн:
- не потребуется много времени. Расчет происходит за секунду.
- не надо искать способ решения. Необходимая формула уже заложена в калькуляторе.
- не стоит беспокоиться за потерю данных между действиями. Система вычислений происходит за 1 раз после ввода необходимых значений.
Вам предоставляется пошаговый расчет и ответ без погрешностей.
Нахождение вектора онлайн-калькулятором
Решение векторов онлайн пригодится ученикам школ, изучающим тему на уроках геометрии. При подготовке домашних заданий, чтобы проверить самостоятельно решенный пример, можно ввести исходные данные в калькулятор и рассчитать автоматически. Такой способ самопроверки эффективен, так как в случае несовпадения ответов или затруднений в понимании есть возможность изучить способ решения.
Студентам посчитать вектор онлайн часто необходимо в качестве промежуточного действия в составной задаче. На быстро полученном точном ответе базируются последующие вычисления.
Не всегда для решения задания с векторами можно обойтись расчетами, на которых построены калькуляторы. В таких случаях обращайтесь в Zaochnik:
- консультант расскажет об условиях сотрудничества и предложит скидку на услуги;
- преподаватель-математик выполнит необходимый вид работы к указанному сроку;
- отдел контроля качества проверит итоговый файл;
- вы получите решенные задачи по выгодной цене.
Мы сотрудничаем с преподавателями математики школ, университетов, инженерами-проектировщиками, поэтому сможем подобрать подходящего исполнителя конкретно для вашей работы.
Решить треугольник Онлайн по координатам
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Онлайн калькуляторы векторов
Данный раздел содержит калькуляторы, позволяющие выполнять все основные действия над
векторами. В частности, с помощью данных калькуляторов можно вычислять скалярное, векторное и смешанное произведения векторов, раскладывать вектора по базису, проверять их ортогональность, компланарность и др. Всего представлено 19 калькуляторов и для каждого предусмотрено подробное решение соответствующей задачи.
Операции над векторами
19
Сложение векторов
Калькулятор позволяет складывать вектора, заданные в координатной форме.
Разность векторов
Калькулятор позволяет вычитать вектора, заданные в координатной форме.
Модуль (длина) вектора
Калькулятор находит модуль (длину) вектора с описанием подробного решения на русском языке.
Угол между векторами
Калькулятор позволяет найти угол между векторами. Подробное решение также имеется.
Проекция вектора
Калькулятор вычисляет проекцию вектора на ось или на другой вектор.
