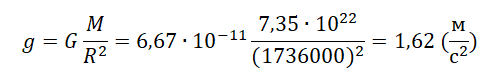Как найти высоту из формулы закона всемирного тяготения
Найдите правильный ответ на вопрос ✅ «Как найти высоту из формулы закона всемирного тяготения …» по предмету 📘 Физика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Содержание
- Как найти начальную высоту тела над поверхностью земли свободное падение
- Физические законы свободного падения
- Формула расчета высоты
- Пример расчета
- Итог
- Как найти начальную высоту тела над поверхностью Земли при свободном падении
- Формула для вычисления начальной высоты
- Пример вычислений
- Погрешность вычислений
- Выводы
- Как найти начальную высоту тела над поверхностью земли свободное падение
- Формула для вычисления начальной высоты
- Пример вычисления начальной высоты
- Другие способы вычисления начальной высоты
- Общий итог
Как найти начальную высоту тела над поверхностью земли свободное падение

Когда тело начинает свое движение под воздействием силы тяжести, оно движется с постоянным ускорением, которое называется свободное падение. Как известно, при свободном падении на тело действует только сила тяжести, поэтому процесс падения можно считать одинаковым для всех тел. Каким образом можно измерить начальную высоту тела над поверхностью земли при свободном падении?
Физические законы свободного падения

Для начала, нужно знать, что при свободном падении на тело действует ускорение, которое принимает одинаковые значения для любого тела на любой высоте. Согласно закону свободного падения, ускорение свободного падения на поверхности Земли составляет 9,81 м/с². Таким образом, если мы знаем время, которое тело находится в свободном падении, мы можем расчитать высоту, на которой оно находилось в начале движения.
Формула расчета высоты
Существует формула, которая позволяет расчитать начальную высоту тела над поверхностью земли при свободном падении:
h = (g * t²) / 2
Где:
- h — начальная высота тела над поверхностью земли
- g — ускорение свободного падения (9,81 м/с²)
- t — время свободного падения
Данная формула основана на формуле движения при постоянном ускорении:
S = v₀t + (at²) / 2
Где:
- S — расстояние, пройденное телом
- v₀ — начальная скорость тела (0 м/с)
- t — время свободного падения
- a — ускорение свободного падения (9,81 м/с²)
Считается, что начальная скорость тела при свободном падении равна нулю, поэтому данная формула упрощается и превращается в формулу расчета высоты.
Пример расчета
Допустим, мы бросаем мячик с балкона на 3-м этаже высотного здания. Мы хотим узнать высоту, на которой находился мячик в начале свободного падения.
Для этого мы измеряем время свободного падения, которое равно 4 секундам. Просчитаем высоту по формуле:
h = (9,81 * 4²) / 2 = 78,48 м
Таким образом, начальная высота мячика над поверхностью земли составляет 78,48 метров.
Итог
Найти начальную высоту тела над поверхностью земли при свободном падении можно, применив соответствующую формулу:
h = (g * t²) / 2
Где:
- h — начальная высота тела над поверхностью земли
- g — ускорение свободного падения (9,81 м/с²)
- t — время свободного падения
Знание данной формулы может оказаться полезным в различных ситуациях, связанных с основными законами физики. Однако, для корректных расчетов необходимо учитывать определенные условия, например, влияние атмосферного давления и температуры воздуха, которые могут незначительно влиять на значение ускорения свободного падения.
Как найти начальную высоту тела над поверхностью Земли при свободном падении
Свободное падение — это движение тела в направлении земной поверхности под действием только силы тяжести. При этом начальная скорость тела равна нулю, а его конечная скорость — скорости свободного падения. Одним из важных параметров, связанных со свободным падением, является начальная высота тела над поверхностью земли. Эта информация может быть полезной при решении различных задач в физике и инженерии.
Формула для вычисления начальной высоты

Для того чтобы вычислить начальную высоту тела над поверхностью земли, необходимо знать значения следующих параметров:
- Ускорение свободного падения (g) — примерное значение — 9,8 м/с2
- Время падения (t) — время, за которое тело падает до земной поверхности
- Конечная скорость тела (v) — скорость, которую тело имеет перед ударом о землю
Формула для вычисления начальной высоты тела над поверхностью земли выглядит следующим образом:
h = (v2 — 0)/(2g)
Где h — начальная высота, v — конечная скорость, g — ускорение свободного падения.
Пример вычислений
Для лучшего понимания как работает формула для вычисления начальной высоты тела над поверхностью земли, представим, что у нас есть следующие данные:
- Ускорение свободного падения (g) — 9,8 м/с2
- Время падения (t) — 4 секунды
- Конечная скорость тела (v) — 39,2 м/с
Теперь, используя формулу, мы можем вычислить начальную высоту:
h = (39,22 — 0)/(2×9,8) = 78,4 м

Таким образом, начальная высота тела над поверхностью земли равна 78,4 метра.
Погрешность вычислений
При использовании формулы для вычисления начальной высоты тела над поверхностью земли при свободном падении необходимо учитывать возможную погрешность вычислений. Она может быть вызвана несколькими факторами, такими как:
- Влияние атмосферного давления и сопротивления воздуха
- Погрешность измерения времени и скорости
- Учет неровностей и ландшафтных особенностей земной поверхности
Учитывая все эти факторы, рекомендуется использовать полученные значения только в тех случаях, когда погрешность вычислений не существенна для решения поставленных задач.
Выводы
Начальная высота тела над поверхностью земли при свободном падении может быть вычислена с помощью соответствующей формулы, использующей значения конечной скорости, времени падения и ускорения свободного падения. При вычислениях следует учитывать возможную погрешность, вызванную различными факторами, такими как сопротивление воздуха и неровности местности.
Как найти начальную высоту тела над поверхностью земли свободное падение
Свободное падение — это движение тела, при котором оно движется под влиянием силы тяжести без начальной скорости в вертикальном направлении. В подобном движении тела важным параметром является начальная высота над поверхностью Земли. В этой статье мы рассмотрим, как найти начальную высоту тела, падающего под действием силы тяжести.
Формула для вычисления начальной высоты
Для вычисления начальной высоты над поверхностью Земли при свободном падении тела используется следующая формула:
h = (1/2) * g * t^2
Где:
- h — начальная высота над поверхностью Земли, метры
- g — ускорение свободного падения, 9,81 м/с^2
- t — время свободного падения, секунды
Пример вычисления начальной высоты
Давайте рассмотрим пример. Предположим, что мы бросаем камень с высоты 100 метров. Какова будет начальная высота над поверхностью Земли?
1. Вычисляем время свободного падения:
t = √(2h/g)
t = √(200/9,81)
t ≈ 4,52 секунды
2. Подставляем время свободного падения в формулу:
h = (1/2) * g * t^2
h = (1/2) * 9,81 * (4,52)^2
h ≈ 100 метров

Таким образом, мы получили, что начальная высота камня над поверхностью Земли составляет 100 метров, как и было указано в условии примера.
Другие способы вычисления начальной высоты
Наряду с формулой, рассмотренной выше, существуют и другие способы для вычисления начальной высоты тела при свободном падении. Вот некоторые из них:
- Вычисление по скорости: h = (v^2) / (2g), где v — начальная скорость тела при его бросании или падении;
- Использование высотометра: прибор для измерения высоты над уровнем моря может служить для вычисления начальной высоты при свободном падении тела, например, при бросании камня вниз с вершины горы.
Общий итог

Начальная высота тела над поверхностью Земли при свободном падении может быть вычислена с помощью формулы h = (1/2) * g * t^2. Для вычисления необходимо знать ускорение свободного падения и время свободного падения. Также существуют и другие способы для вычисления начальной высоты, например, по скорости или с использованием высотометра. Надеюсь, эта статья была для вас полезна.
Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.
Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.
Закон всемирного тяготения
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.
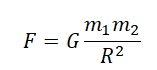
F — сила всемирного тяготения, m1 и m2 — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10–11 Н ∙ м2/кг2).
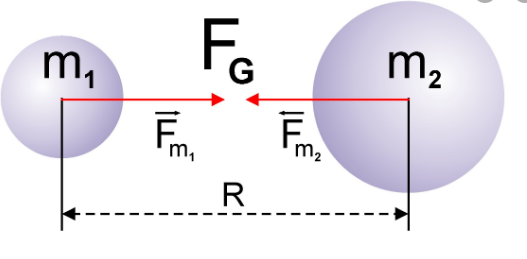
Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.
Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m1 = 1 кг и m2 = 1 кг, то F = G.
G = 6,67∙10–11 Н ∙ м2/кг2.
Сила тяжести
Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.
Сила тяжести — сила, с которой Земля притягивает к себе тела.
Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.

Расчет силы тяжести на Земле
Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:
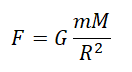
Вывод формулы ускорения свободного падения
Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.
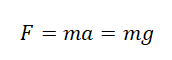
Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.
Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:
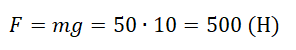
Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:
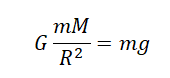
Отсюда:
Формула расчета ускорения свободного падения
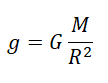
Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.
Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙1022 кг.
Переведем километры в метры: 1736 км = 1736000 м.
Первая космическая скорость
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.
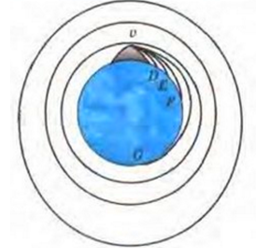
ОпределениеПервая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.
Вывод формулы первой космической скорости
Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:
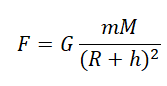
Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.
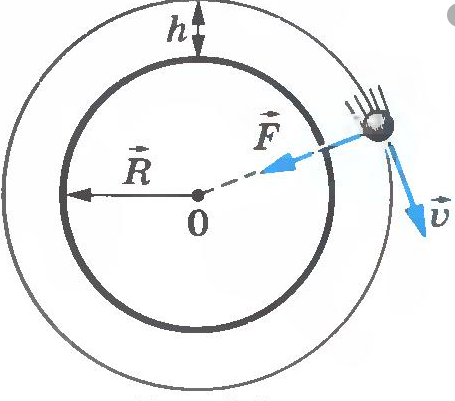
Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:
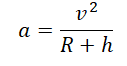
Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:
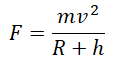
Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:
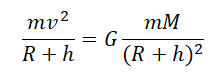
Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:
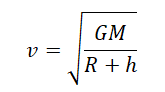
Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.
Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:
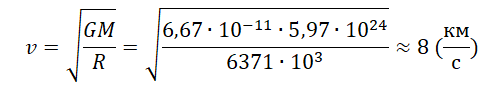
8 км/с — первая космическая скорость Земли.
Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙1024 кг, а ее радиус равен 6052 км.
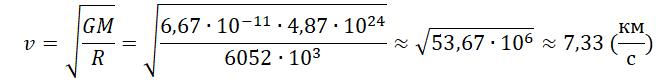
Задание EF18521
Сила гравитационного притяжения между двумя шарами, находящимися на расстоянии 2 м друг от друга, равна 9 нН. Какова будет сила притяжения между ними, если расстояние увеличить до 6 м? Ответ выразите в наноньютонах (нН).
Алгоритм решения
- Записать исходные данные.
- Записать закон всемирного тяготения.
- Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
- На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.
Решение
Запишем исходные данные:
- Расстояние между двумя шарами в первом случае: R1 = 2 м.
- Расстояние между двумя шарами во втором случае: R2 = 6 м.
- Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.
Запишем закон всемирного тяготения:
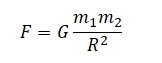
Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m1 и m2.
R2 больше R1 втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 32 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17569
Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?
а) 7F
б) 9F
в) 12F
г) 16F
Алгоритм решения
1.Записать закон всемирного тяготения.
2.Применить закон всемирного тяготения для первой и второй пары звезд.
3.Из каждого выражения выразить расстояние между звездами.
4.Приравнять правые части уравнений и вычислить силу притяжения между второй парой звезд.
Решение
Закон всемирного тяготения выглядит так:
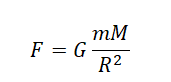
Примерим этот закон для первой и второй пары звезд:
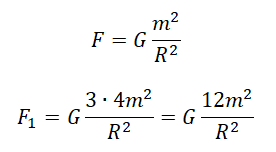
Выразим квадраты радиусов, так как они в обоих случаях одинаковые:
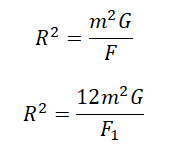
Приравняем правые части выражений и выразим силу притяжения во втором случае:
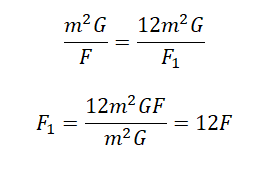
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18678
Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличилась |
| 2) | уменьшилась |
| 3) | не изменилась |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость
спутника |
Потенциальная энергия спутника |
Алгоритм решения
1.Записать закон всемирного тяготения и формулу центростремительного ускорения для движения тела по окружности с постоянной по модулю скоростью.
2.Установить зависимость скорости от высоты спутника над поверхностью Земли.
3.Записать формулу потенциальной энергии и установить, как она зависит от высоты.
Решение
На спутник действует сила притяжения Земли, которая сообщает ему центростремительное ускорение:
F=maц=GmM(R+h)2
Отсюда центростремительное ускорение равно:
aц=GM(R+h)2
Но центростремительное ускорение также равно:
aц=v2(R+h)
Приравняем правые части выражений и получим:
GM(R+h)2=v2(R+h)
v2=MG(R+h)(R+h)2=MG(R+h)
Квадрат скорости спутника обратно пропорционален радиусу вращения. Следовательно, при увеличении высоты увеличивается радиус вращения, а скорость уменьшается.
Потенциальная энергия спутника определяется формулой:
Ep = mgh
Видно, что потенциальная энергия зависит от высоты прямо пропорционально. Следовательно, при увеличении высоты потенциальная энергия спутника тоже увеличивается.
Верная последовательность цифр в ответе: 21.
Ответ: 21
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17578
Искусственный спутник обращается вокруг планеты по круговой орбите радиусом 4000 км со скоростью 3,4 км/с. Ускорение свободного падения на поверхности планеты равно 4 м/с2. Чему равен радиус планеты? Ответ запишите в километрах.
Алгоритм решения
1.Записать исходные данные. Перевести единицы измерения в СИ.
2.Записать формулу ускорения свободного падения и выразить через нее радиус планеты.
3.Записать формулу, раскрывающая взаимосвязь между линейной скоростью и радиусом окружности, по которой движется тело.
4.Записать закон всемирного тяготения применительно к спутнику.
5.Вывести формулу для расчета радиуса планеты.
6.Подставить известные данные и произвести вычисление.
Решение
Запишем исходные данные:
• Линейная скорость спутника: v = 3,4 км/с, или 3,4∙103 м/с.
• Радиус орбиты спутника: Rо = 4000 км, или 4∙106 м.
• Ускорение свободного падения у поверхности планеты: g = 4 м/с2.
Ускорение свободного падения определяется формулой:
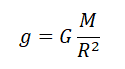
Отсюда радиус равен:
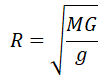
Линейная скорость и радиус орбиты связываются формулой:
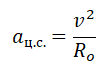
Используя закон всемирного тяготения, запишем силы, с которой притягивается спутник к планете:
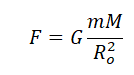
Согласно второму закону Ньютона, сила — это произведение массы на ускорение тела. Следовательно:
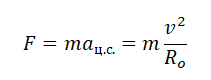
Отсюда:
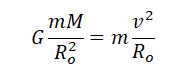
Поделим обе части выражения на массу спутника и радиус его орбиты. Получим:
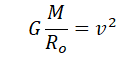
Из этой формулы выразим массу планеты:
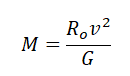
Подставим массу планеты в формулу для нахождения ее радиуса:
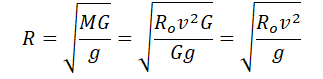
Подставляем известные данные и вычисляем:
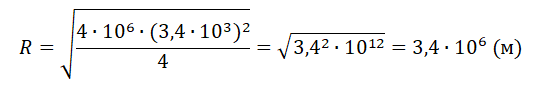
Этот радиус соответствует 3400 км.
Ответ: 3400
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 18k
Лучший ответ
Эдгар Зотиков
Мыслитель
(8025)
7 лет назад
Нужно условие задачи
Алиса БагроваЗнаток (328)
7 лет назад
кран поднял предмет, который весит 24 кН, проделав при этом работу 360 кДж. На какую высоту подняли предмет
Эдгар Зотиков
Мыслитель
(8025)
A=F*H —-> H=A/F=360000дж/24000н=15 м
Остальные ответы
Алексей Данов
Мастер
(2013)
7 лет назад
Условия нужны для точности.
Но есть формула, которая связывает силу тяжести Fт, высоту и потенциальную энергию (или работу силы по подъему массы на высоту h)
Eп=m g h=Fт h (Fт=mg)
Содержание:
Закон всемирного тяготения:
В таблице представлены орбитальные скорости планет и карликовых планет Солнечной системы. Исследуя эту информацию, с легкостью можно определить, что небесные тела этой системы, близко расположенные к Солнцу, имеют более высокую орбитальную скорость.
Орбитальная скорость Луны вокруг Земли, по сравнению со скоростями из повседневной жизни, так же очень большая: -3682,8 км/час. Однако эта скорость во много раз меньше скорости Земли вокруг Солнца.
| Планеты и карликовые планеты | Орбитальная скорость | |
| км/с | км/с | |
| Меркурий | 47,87 | 172 332 |
| Венера | 35,02 | 126 072 |
| Земля | 29,78 | 107 208 |
| Марс | 24,13 | 86 868 |
| Церера | 17,88 | 64 368 |
| Юпитер | 13,07 | 47 052 |
| Сатурн | 9,69 | 34 884 |
| Уран | 6,81 | 24 516 |
| Нептун | 5,43 | 19 548 |
| Плутон | 4,67 | 16 812 |
| Хаумеа | 4,48 | 16 128 |
| Макемаке | 4,41 | 15 876 |
| Эрида | 3,44 | 12 384 |
Вы знаете, что все тела во Вселенной, имеющие массу – звезды, галактики, Солнце и планеты, тела Земной системы, молекулы, атомы и другие, взаимно притягиваются друг к другу с силой, называемой силой тяготения (или гравитационной силой). Исследовав, от каких величин и как зависит эта сила, Исаак Ньютон сформулировал закон всемирного тяготения.
Закон всемирного тяготения
Между любыми двумя материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними:
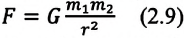
Где 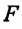
Гравитационная постоянная
Единица гравитационной постоянной в СИ:
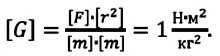
Гравитационная постоянная численно равна силе притяжения друг к другу двух материальных точек массами по 1 кг каждый, если расстояние между ними равно 1 м.
Численное значение гравитационной постоянной опытным путем определил английский ученый Генри Кавендиш (1731—1810) в 1798 году. Это значение одинаково для всех тел во Вселенной вне зависимости от их размеров и масс:
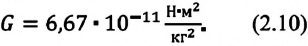
Как видно, численное значение гравитационной постоянной очень мало. Поэтому между телами с относительно малыми массами сила притяжения не чувствуется. Эта сила принимает ощутимые значения при взаимодействии тел с очень большой массой, например, между звездой и планетой, планетой и спутником и т.д.
Формула закона всемирного тяготения
Сила притяжения между двумя произвольными телами, не являющимися материальными точками при данных условиях, также определяется формулой закона всемирного тяготения. В этом случае эти тела рассматриваются как совокупность материальных точек, вычисляются силы притяжения между всеми материальными точками этих тел, результаты вычислений суммируются и определяются сила притяжения между этими телами. Такие вычисление представляет собой сложную математическую операцию. Однако формула Всемирного тяготения легко применяется для тел шарообразной формы. За расстояние между телами при этом принимается расстояние между их центрами (а). Поэтому для вычисления силы притяжения между произвольным телом и Землей можно применить формулу закона всемирного тяготения. В этом случае расстояние между ними берется до центра Земли: 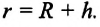 Силы взаимодействия между Землей и телом,
Силы взаимодействия между Землей и телом, 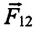 и
и 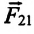 направлены вдоль линии, соединяющей эти тела.
направлены вдоль линии, соединяющей эти тела.
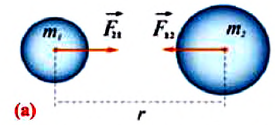
Согласно III закону Ньютона 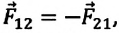 их модули равны:
их модули равны:
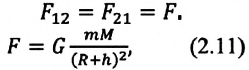
Где 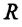 — радиус земного шара,
— радиус земного шара, 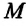 – масса Земли,
– масса Земли, 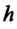 — расстояние от поверхности Земли до центра тела, вдоль радиуса. Для тел, находящихся на поверхности Земли
— расстояние от поверхности Земли до центра тела, вдоль радиуса. Для тел, находящихся на поверхности Земли 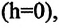 закон всемирного тяготения записывается в виде:
закон всемирного тяготения записывается в виде:
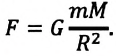
Измерение гравитационной постоянной
С этой целью Г. Кавендиш использовал крутильные весы. Схема весов показана на рисунке: на концах стержня длиной 2 м он установил два свинцовых шарика массой по 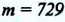 г каждый и диаметром приблизительно 5 см. Стержень подвешен на упругой нити. У каждого шарика разместили большие свинцовые шары массами по
г каждый и диаметром приблизительно 5 см. Стержень подвешен на упругой нити. У каждого шарика разместили большие свинцовые шары массами по 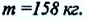 В результате притяжения между большими и малыми шарами нить закручивается на очень небольшой угол. Угол поворота определяется перемещением по шкале светового “зайчика”, отраженного от плоского зеркала, закрепленного на нити, (b).
В результате притяжения между большими и малыми шарами нить закручивается на очень небольшой угол. Угол поворота определяется перемещением по шкале светового “зайчика”, отраженного от плоского зеркала, закрепленного на нити, (b).
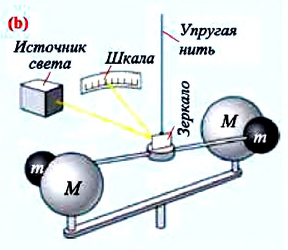
Зная угол поворота, можно определить силу упругости 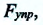 возникающую в результате закручивания нити. Сила упругости уравновешивает силу притяжения между шарами, т.е. эти силы равны по модулю:
возникающую в результате закручивания нити. Сила упругости уравновешивает силу притяжения между шарами, т.е. эти силы равны по модулю: 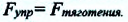
Таким образом, ученый, подставив известные величины в формулу закона всемирного тяготения, получил для гравитационной постоянной значение, очень близкое к его современному значению:
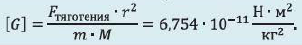
Что такое закон всемирного тяготения
Все тела во Вселенной, как небесные, так и находящиеся на Земле, взаимно притягиваются. Даже если мы не замечаем притягивания между обычными предметами, которые окружают нас в повседневной жизни (например, между книгами, тетрадями, мебелью и т. п.), то это потому, что оно в таких случаях очень слабое.
Взаимодействие, свойственное всем телам во Вселенной и проявляющееся взаимным притягиванием друг к другу, называют гравитационным, а само явление всемирного тяготения — гравитацией (лат. gravitas — «тяжесть»).
Гравитационное взаимодействие осуществляется с помощью особенного вида материи, который называют гравитационным полем. Такое поле существует вокруг любого тела – планеты, камня, человека или листа бумаги. При этом тело, создающее гравитационное поле, действует им на любое другое тело так, что у того появляется ускорение, всегда направленное к источнику поля. Появление такого ускорения и значит, что между телами возникает притяжение.
Гравитационное поле не следует путать с электромагнитными полями, существующими вокруг наэлектризованных тел, проводников с током и магнитов.
Интересной особенностью гравитационного поля, которую не имеют электромагнитные поля, является его всепроникающая способность. Если от электрических и магнитных полей можно защититься с помощью специальных металлических экранов, то от гравитационного поля защититься ничем нельзя: оно проникает сквозь любые материалы.
Выражение для силы притяжения Исаак Ныотон получил еще в 1666 г., когда ему было 24 года. Сначала ученый установил, как зависит от расстояния ускорение свободного падения. Он заметил, что вблизи поверхности Земли, то есть на расстоянии 6400 км от ее центра, это ускорение равно 9,8 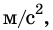 а на расстоянии в 60 раз большем, возле Луны, это ускорение оказывается в 3600 раз меньше, чем на Земле. Но 36 00 =
а на расстоянии в 60 раз большем, возле Луны, это ускорение оказывается в 3600 раз меньше, чем на Земле. Но 36 00 = 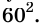 Следовательно, ускорение свободного падения уменьшается обратно пропорционально квадрату расстояния от центра Земли. Но ускорение, по второму закону Ньютона, пропорционально силе. Следовательно, причиной такого уменьшения ускорения является аналогичная зависимость силы притяжения от расстояния.
Следовательно, ускорение свободного падения уменьшается обратно пропорционально квадрату расстояния от центра Земли. Но ускорение, по второму закону Ньютона, пропорционально силе. Следовательно, причиной такого уменьшения ускорения является аналогичная зависимость силы притяжения от расстояния.
Окончательную формулу силы притяжения можно получить, если учесть, что эта сила должна быть пропорциональна массам тел 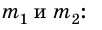
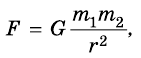
где G – гравитационная постоянная.
Так, Ньютон нашел выражение для силы гравитационного взаимодействия Земли с телами, которые притягивались ею. Но интуиция подсказывала ему, что по данной формуле можно рассчитывать и силу притяжения, действующую между любыми другими телами Вселенной, если только их размеры малы по сравнению с расстоянием г между ними. Поэтому он начал рассматривать полученное выражение как закон всемирного тяготения, который выполняется и для небесных тел, и для тел на Земле.
Сила гравитационного притяжения любых двух частиц прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними:
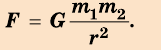
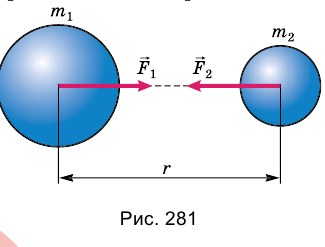
Закон всемирного тяготения сформулирован для частиц, размеры которых значительно меньше расстояния г между ними. Однако одна особенность закона дает возможность использовать его и в некоторых иных случаях. Такой особенностью является обратно пропорциональная зависимость силы притяжения именно от квадрата расстояния между частицами, а не от третьей или четвертой степени расстояния. Расчеты показывают, что благодаря этой особенности формулу 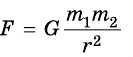 можно применять еще и для расчета силы притяжения шарообразных тел со сферически симметричным распределением вещества, находящихся на любом расстоянии друг от друга. Под г в этом случае следует понимать не расстояние между ними, а расстояние между их центрами (рис. 281).
можно применять еще и для расчета силы притяжения шарообразных тел со сферически симметричным распределением вещества, находящихся на любом расстоянии друг от друга. Под г в этом случае следует понимать не расстояние между ними, а расстояние между их центрами (рис. 281).
Формула 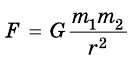 выполняется и для случая, когда сферическое тело произвольных размеров взаимодействует с некоторой материальной точкой. Это и дает возможность применять формулу закона всемирного тяготения для расчета силы, с которой земной шар притягивает к себе окружающие тела.
выполняется и для случая, когда сферическое тело произвольных размеров взаимодействует с некоторой материальной точкой. Это и дает возможность применять формулу закона всемирного тяготения для расчета силы, с которой земной шар притягивает к себе окружающие тела.
Когда Ньютон открыл закон всемирного тяготения, он не знал ни одного числового значения масс небесных тел, в том числе и Земли. Неизвестно ему было и значение постоянной.
Вместе с тем, гравитационная постоянная G имеет для всех тел Вселенной одно и то же значение и является одной из фундаментальных физических констант. Каким же образом можно определить ее значение? Из закона всемирного тяготения следует, что 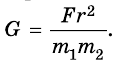 . Чтобы вычислить G, следует измерить силу притяжения F между телами известных масс
. Чтобы вычислить G, следует измерить силу притяжения F между телами известных масс 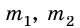 и расстояние r между ними.
и расстояние r между ними.
Первые измерения гравитационной постоянной были осуществлены в середине XVIII в. Оценить, правда очень грубо, значение G в то время удалось в результате рассмотрения притягивания маятника к горе, масса которой была определена с помощью геологических методов.
Точные измерения гравитационной постоянной впервые осуществил в 1798 г. Генри Кавендиш – английский физик, член Лондонского королевского общества. С помощью так называемых крутильных весов (рис. 282) ученый по углу закручивания нити А сумел измерить ничтожно малую силу притяжения между маленькими и большими металлическими шарами. Для этого ему пришлось использовать очень чувствительные приборы, потому что даже слабые воздушные потоки могли исказить измерение. Во избежание посторонних влияний, Кавендиш разместил свои приборы в ящике, который оставил в комнате, а сам проводил наблюдение за приборами с помощью телескопа из другого помещения.
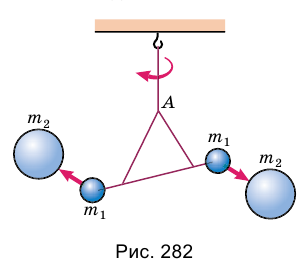
Опыты показали, что 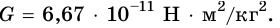
Физическое содержание гравитационной постоянной заключается в том, что она определяется силой, с которой притягиваются два тела массами 1 кг каждое, находящиеся на расстоянии 1 м друг от друга.
Если на тело действует только одна сила, направленная вниз (а все другие уравновешены), то оно осуществляет свободное падение. Ускорение свободного падения можно определить, применив второй закон Ньютона:
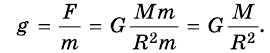
Отсюда следует, что ускорение свободного падения 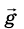 не зависит от массы m тела, а следовательно, оно одинаково для всех тел. Такое удивительное свойство силы всемирного притяжения, а значит, и силы притяжения. Ее опытным путем вычислил еще Галилей. Удивительно, потому что по второму закону Ньютона ускорение тела должно быть обратно пропорционально массе. Но сама сила притяжения пропорциональна массе тела, на которое она действует. Именно поэтому ускорение свободного падения одинаково для всех тел.
не зависит от массы m тела, а следовательно, оно одинаково для всех тел. Такое удивительное свойство силы всемирного притяжения, а значит, и силы притяжения. Ее опытным путем вычислил еще Галилей. Удивительно, потому что по второму закону Ньютона ускорение тела должно быть обратно пропорционально массе. Но сама сила притяжения пропорциональна массе тела, на которое она действует. Именно поэтому ускорение свободного падения одинаково для всех тел.
Теперь для силы притяжения можно записать выражение: 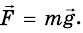
По существу говоря, формула 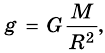 , как и второй закон Ньютона, справедлива, когда свободное падение рассматривается относительно инерциальной системы отсчета.
, как и второй закон Ньютона, справедлива, когда свободное падение рассматривается относительно инерциальной системы отсчета.
Приведенные значения показывают, что ускорение свободного падения в разных районах земного шара отличается очень мало от значения, вычисленного по формуле 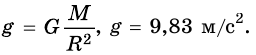
Поэтому при грубых подсчетах пренебрегают неинерциальностые системы отсчета, связанной с поверхностью Земли, и отличием формы Земли от сферической. Ускорение свободного падения считают всюду одинаковым и вычисляют по формуле 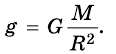
В некоторых районах земного шара ускорение свободного падения отличается от приведенного выше значения еще по одной причине. Такие отклонения наблюдаются там, где в недрах Земли залегают породы, плотность которых больше или меньше средней плотности Земли. Там, где есть залежи пород, имеющих большую плотность, значение g больше. Это дает возможность геологам по измерениям значения g находить месторождения полезных ископаемых.
Следовательно, сила притяжения, а значит, и ускорение свободного падения изменяются с отдалением от поверхности Земли. Если тело находится на высоте h над поверхностью Земли, то выражение для модуля ускорения свободного падения g следует записывать следующим образом:
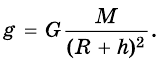
Так, на высоте 300 км ускорение свободного падения уменьшается на 1 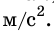 . Из формулы видно, что для высот в несколько десятков или сотен метров над Землей, и даже многих километров, сила притяжения может считаться постоянной, независимо от положения тела. Поэтому свободное падение близ Земли можно считать равноускоренным движением.
. Из формулы видно, что для высот в несколько десятков или сотен метров над Землей, и даже многих километров, сила притяжения может считаться постоянной, независимо от положения тела. Поэтому свободное падение близ Земли можно считать равноускоренным движением.
Движение тела под действием силы притяжения: тело движется по вертикали. Если предоставить телу начальную скорость д0, направленную вверх, то это не изменит ни направления, ни значения ускорения тела, потому что толчок вверх не может изменить силу притяжения. В обоих случаях траекторией тела является вертикальная прямая.
Решая задачи на такое движение, за тело отсчета удобно выбирать Землю с началом отсчета на ее поверхности или в любой точке выше или ниже от поверхности, а координатную ось направлять по вертикали вверх или вниз. Высоту тела над определенной поверхностью принято обозначать буквой h (рис. 283).
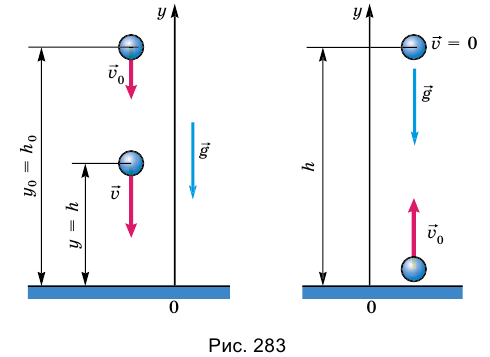
Тогда координата y тела – это просто его высота h над точкой начала отсчета. Проекция вектора перемещения тела соответствует изменению высоты и равна h – 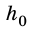 , где
, где 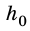 – начальная высота.
– начальная высота.
Формулы для вычисления координат (высот) и скоростей ничем не отличаются от формул для прямолинейного равноускоренного движения.
Координата тела (высота):
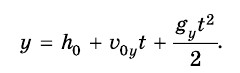
Скорость тела в любой момент времени:
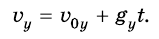
Скорость тела в любой точке траектории:
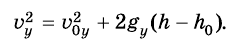
Проекция 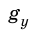 положительна, если ось Оу направлена вниз, и отрицательна, если ось Оу направлена вверх. Проекции
положительна, если ось Оу направлена вниз, и отрицательна, если ось Оу направлена вверх. Проекции 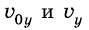 положительны, если векторы скоростей направлены вдоль оси Оу, и отрицательны, если векторы скоростей направлены противоположно оси Оу.
положительны, если векторы скоростей направлены вдоль оси Оу, и отрицательны, если векторы скоростей направлены противоположно оси Оу.
- Заказать решение задач по физике
Движение тела под действием силы притяжения: начальная скорость тела направлена под углом к горизонту. Часто приходится рассматривать движения тел, начальная скорость которых не параллельна силе притяжения, а направлена под определенным углом к ней (или к горизонту). Когда, например, спортсмен толкает ядро, бросает диск или копье, он придает этим предметам именно такую скорость. При артиллерийской стрельбе стволы пушек имеют определенный угол поднятия, так что снаряд в стволе также получает начальную скорость, направленную под углом к горизонту.
Будем считать, что силой сопротивления воздуха можно пренебречь. Как в этом случае движется тело?
На рисунке 284 показан стробоскопический снимок шарика, брошенного под углом 60° к горизонту. Соединив последовательно положения шарика плавной кривой, получим траекторию движения шарика – параболу.
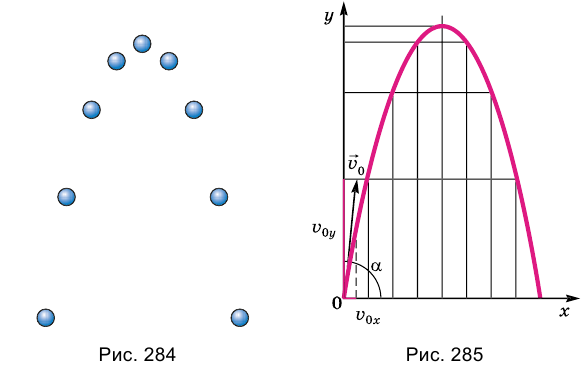
Если пренебречь влиянием воздуха на движение тела, то на тело, брошенное под углом к горизонту, как и на свободно падающее тело, или на тело, которое получило начальную скорость, направленную вертикально, действует только сила притяжения. Как бы ни двигалось тело, сила притяжения может сообщить ему только ускорение 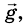 , направленное вниз. Этим определяются и траектория движения тела и характер его движения.
, направленное вниз. Этим определяются и траектория движения тела и характер его движения.
Предположим, что из некоторой точки О брошено тело с начальной скоростью 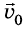 , направленной под углом а к горизонту. Возьмем за начало отсчета координат точку, с которой брошено тело, а за начало отсчета времени – момент бросания. Ось Ох направим горизонтально, а ось Оу – вертикально вверх (рис. 285). Из рисунка видим, что проекции вектора
, направленной под углом а к горизонту. Возьмем за начало отсчета координат точку, с которой брошено тело, а за начало отсчета времени – момент бросания. Ось Ох направим горизонтально, а ось Оу – вертикально вверх (рис. 285). Из рисунка видим, что проекции вектора 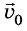 на оси Ох и Оу соответственно равны:
на оси Ох и Оу соответственно равны:
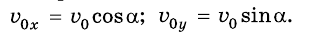
Поскольку на тело действует сила притяжения, то при движении тела будет меняться только проекция 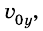 , а проекция
, а проекция 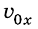 не будет меняться. Поэтому координата х тела с течением времени меняется так же, как при прямолинейном равномерном движении:
не будет меняться. Поэтому координата х тела с течением времени меняется так же, как при прямолинейном равномерном движении:
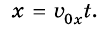
А координата у меняется так же, как при прямолинейном равноускоренном движении:
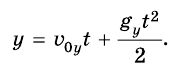
Чтобы найти траекторию движения тела, надо подставить в уравнение значения времени t, какие последовательно увеличиваются, и вычислить координаты х и у для каждого значения t, если известны значения модуля начальной скорости 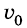 и угла а. По найденным значениям х и у наносим точки, которые изображают последовательные положения тела. Соединяя их плавной кривой, получим траекторию движения тела. Она будет подобна изображенной на рисунке 285.
и угла а. По найденным значениям х и у наносим точки, которые изображают последовательные положения тела. Соединяя их плавной кривой, получим траекторию движения тела. Она будет подобна изображенной на рисунке 285.
Что будет если тело брошено горизонтально
Тело можно бросить и так, что его начальная скорость 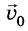 будет направлена горизонтально (а = 0). Например, так направлена начальная скорость тела, оторвавшегося от самолета, который летит горизонтально. Легко выяснить, по какой траектории будет двигаться такое тело. Для этого обратимся опять к рисунку 285, на котором изображена траектория движения тела, брошенного под углом а к горизонту. В наивысшей точке параболы скорость тела как раз и направлена горизонтально. А за этой точкой тело движется по правой ветви параболы. Очевидно, что и любое тело, брошенное горизонтально, также будет двигаться по ветви параболы (рис. 286).
будет направлена горизонтально (а = 0). Например, так направлена начальная скорость тела, оторвавшегося от самолета, который летит горизонтально. Легко выяснить, по какой траектории будет двигаться такое тело. Для этого обратимся опять к рисунку 285, на котором изображена траектория движения тела, брошенного под углом а к горизонту. В наивысшей точке параболы скорость тела как раз и направлена горизонтально. А за этой точкой тело движется по правой ветви параболы. Очевидно, что и любое тело, брошенное горизонтально, также будет двигаться по ветви параболы (рис. 286).
Траекторию движения тел, брошенных горизонтально или под углом к горизонту, можно показать на опыте. Сосуд, заполненный водой, размещают на определенной высоте над столом и соединяют его резиновой трубкой с наконечником, который имеет кран (рис. 287). Выпущенные струи воды непосредственно показывают траектории частиц воды. Таким образом можно наблюдать траекторию для разных значений угла а и скорости 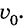

Мы рассмотрели несколько примеров движения тел под действием силы притяжения. Во всех случаях тело движется с ускорением свободного падения, которое не зависит от того, имело ли тело еще и скорость в горизонтальном направлении или нет. Например, пуля, выпущенная стрелком из винтовки в горизонтальном направлении, упадет на землю одновременно с пулей, которую случайно уронил стрелок в момент выстрела. Но вторая пуля упадет у ног стрелка, а пуля, вылетевшая из ствола винтовки, – на определенном расстоянии.
История:
Попытки объяснить наблюдаемую картину мира, и прежде всего строение Солнечной системы, делали многие ученые. Что связывает планеты и Солнце в единую систему? Каким законам подчиняется их движение?
Во II в. н. э. древнегреческий ученый Клавдий Птолемей разработал геоцентрическую систему мира, согласно которой все наблюдаемые перемещения небесных светил объяснялись их движением вокруг неподвижной Земли.
В XVI в. польский астроном Миколай Коперник предложил гелиоцентрическую систему мира: в центре находится Солнце, а вокруг него движутся планеты и их спутники. Что же удерживает планеты, в частности Землю, когда они движутся вокруг Солнца?
Если придерживаться утверждений Аристотеля и связывать силу притяжения тел со скоростью их движения, а не с ускорением, то причиной движения планет является именно направление скорости.
Ньютон связал силу с ускорением. Именно силу притяжения Солнца естественно считать причиной вращения вокруг него Земли и планет.
Но не только планеты притягиваются к Солнцу. Солнце также притягивается планетами. Да и сами планеты взаимодействуют между собой. Одним из первых, кто это понял, был английский ученый Роберт Гук. В 1674 г. он писал: «Все небесные тела имеют притяжение, или силу тяготения к своему центру, вследствие чего они не только притягивают собственные части и препятствуют им разлетаться, как наблюдаем на Земле, но притягивают также все другие небесные тела, находящиеся в сфере их действия. Поэтому не только Солнце и Луна имеют влияние на движение Земли, но и Меркурий, и Венера, и Марс, и Юпитер, и Сатурн также своим притяжением имеют значительное влияние на ее движение. Подобным образом и Земля притяжением влияет на движение каждого из этих тел».
В своем труде «Математические начала натуральной философии» Ньютон сформулировал три фундаментальных закона (известны как законы Ньютона). В соответствии с данными законами, все тела Вселенной, как небесные, так и те, которые находятся на Земле, склонны к взаимному тяготению, причем силы, с которыми притягиваются все эти тела, имеют одинаковую природу и подчиняются одному и тому же закону.
Согласно легенде, мысль о всемирном тяготении озарила Ньютона в тот момент, когда он, отдыхая в своем саду, увидел яблоко, которое падает. Рассказывают даже, что знаменитой яблоне, плод которой сумел так «вовремя» упасть к ногам Ньютона, не дали исчезнуть бесследно и кусочки этого дерева якобы хранятся в Англии и в настоящее время.
Открытие закона всемирного тяготения дало возможность Ньютону создать теорию движения небесных тел, основанную на строгих математических доказательствах. Ничего подобного в науке до того времени не было.
Эта теория, бесспорно, поразила современников Ньютона, но у них возник вопрос: почему все тела притягиваются друг к другу? Ответа на него выдающийся физик не дал. «Причину же свойств силы тяготения я до сих пор не мог вывести из явлений, гипотез же я не выдумываю, – писал он в своих “Математических началах”. – Достаточно того, что притяжение в действительности существует, и действует согласно изложенному закону, и является полностью достаточным для объяснения всех движений небесных тел и моря».
Говоря о море, Ньютон имел в виду явление приливов, обусловленных притягиванием воды Луной и Солнцем. За две тысячи лет до Ньютона над причинами этого явления рассуждал Аристотель, который, однако, объяснить его не смог. Для философа это оказалось трагедией. «Наблюдая длительное время это явление со скалы Негро-понта, он, охваченный отчаянием, бросился в море и нашел там добровольную смерть», – утверждал Г. Галилей.
- Свободное падение тела
- Равнодействующая сила и движение тела под действием нескольких сил
- Сила давления в физике и единицы давления
- Механическое давление в физике
- Деформация в физике
- Плотность вещества в физике
- Сила трения в физике
- Вес тела в физике