Определение высоты подъема:
Определим продолжительность
цикла на каждый вариант работ по следующей
аналитической формуле:
![]()
;
где
![]()
время подъема груза и опускания порожнего
ГЗУ на среднюю высоту подъема;
![]()
время опускания груза и подъема порожнего
ГЗУ на среднюю высоту опускания;
![]()
время поворота крана;
![]()
– время на установку порожнего
грейфера на груз (![]()
–
для трюма и
![]()
–
для склада);
![]()
– время на захват груза (![]()
–
для трюма и
![]()
–
для склада);
![]()
– время на направление груженого
грейфера над местом выгрузки (![]()
–
для полувагона и
![]()
–
для склада);
![]()
– время на высыпание груза (![]()
–
для склада и
![]()
–
для полувагона);
![]()
– коэффициент, учитывающий совмещение
операций :
судно – склад
![]()
;
судно – вагон
![]()
;
склад – вагон
![]()
;
Для определения времени
операций необходимо определить высоту
подъема и опускания груза по каждому
варианту работ:
судно – склад:
![]()
;
![]()
.
судно – вагон:
![]()
![]()
склад – вагон:
так как
![]()
(8,7м>3,7м),
то:
![]()
![]()
где
![]()
– осадка судна;
![]()
– средняя высота грузовых помещений;
![]()
– расстояние от причальной стенки до
уровня воды;
![]()
–
высота штабеля;
![]()
– высота вагона от уровня головок
рельса.
Определение времени цикла по вариантам работ:
Определим
![]()
для каждого варианта работ:
судно – склад:
![]()
![]()
![]()
судно – вагон:
![]()
![]()
склад-вагон:
![]()
![]()
![]()
После расчета всех
составляющих определим продолжительность
цикла по каждому варианту работ:
судно – склад:
![]()
.
судно – вагон:
![]()
.
склад – вагон:
![]()
Полученные
данные занесены в таблицу:
|
Вариант работ/показатель |
судно-склад |
судно-вагон |
склад-вагон |
|
|
79,70 |
75,02 |
53,06 |
Циклограмма:
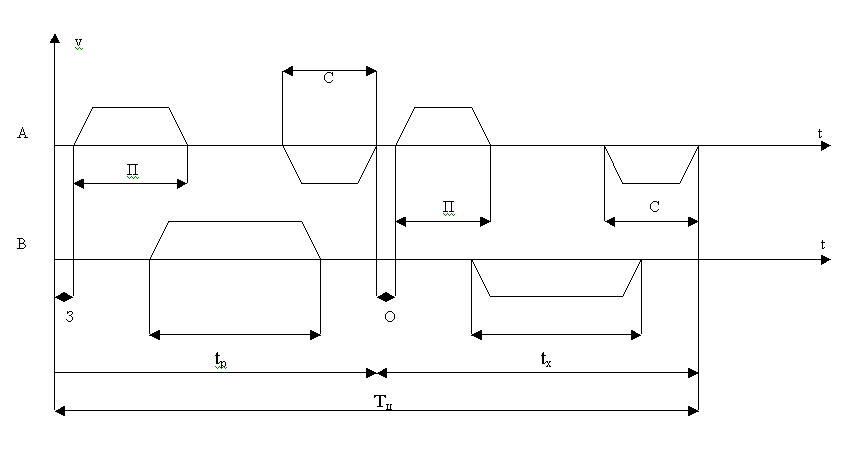
З – захват груза;
П – подъем;
С – спуск;
О – открытие грейфера;
ttрх – соответственно
рабочий и холостой ход;
А – механизм подъема;
В – механизм поворота.
Определение производительности
перегрузочного оборудования причала:
Производительность
перегрузочного оборудования причала
по вариантам работ:
;
где P –
расчетная производительность;
Tц
– время цикла;
G – масса
груза в одном подъеме;
судно – склад:
I слой:
![]()
II слой:
![]()

судно – вагон:
I слой:
![]()
II слой:
![]()
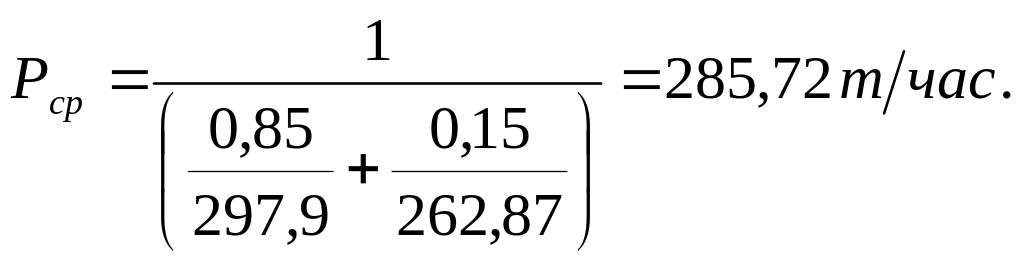
склад – вагон:
I слой:
![]()
II слой:
![]()

Полученные данные
занесены в таблицу:
|
Вариант работ |
Производительность, т/ч |
|
судно-склад |
303,03т/час |
|
судно-вагон |
285,72т/час |
|
склад-вагон |
416,7т/час |
Определим средневзвешенную
производительность крана по обработке
судна и вагонов с учетом коэффициентов
транзита и складочности по формуле:

;


;

Очевидно, что в
подпалубных пространствах судов при
обработке слоя груза менее 1 метра
необходимо применять подгребающие
машины. В данном курсовом проекте для
подачи угля из подпалубного пространства
в просвет люка предполагается использование
трюмного погрузчика ПСГ – 120 на
электрическом приводе. Вес данной машины
составляет 4620 тонн, эксплуатационная
производительность – 120 тонн в час.
Определим необходимое
количество трюмных машин для операций
по разгрузке судов:

.
Проектный вариант:
В качестве проектного варианта в данном
курсовом проекте используется кран
мостовой электрический грейферный г/п
15 тн. группы режима А7 с
грейфером.
Так как грузооборот достаточно большой
(8 млн. тонн) эффективным и рациональным
будет попробовать внедрить схему с
мостовыми кранами, оснащенными грейферами.
Это увеличит интенсивность обработки
транспортных средств.
Технические характеристики перегрузочной
техники и грузозахватного приспособления,
используемые в проектном варианте,
приведены ниже.
Кран мостовой
электрический грейферный г/п 15 тн. группы
режима А7. Данный современный кран
предоставлен компанией «Уралкран»
и является типовым.
-
Название крана
«Уралкран»
Тип подкранового рельса
Р 43 КР 70
Грузоподъемность, т
15
Пролёт крана Lвылета,
м30
Скорость подъема ГЗУ
Vподъем,
м/с1,38
Скорость
передвижения крана Vпередв
крана, м/с15
Скорость передвижения
тележки Vпередв
тележки, м/с1,47
Масса крана, т
44,7
Масса тележки, т
7,1
Масса грейфера, т
До 6
Мощность электродвигателей подъёма
и смыкания, кВт
Мощность электродвигателей передвижения
крана, кВт
Мощность электродвигателей передвижения
тележки, кВт5
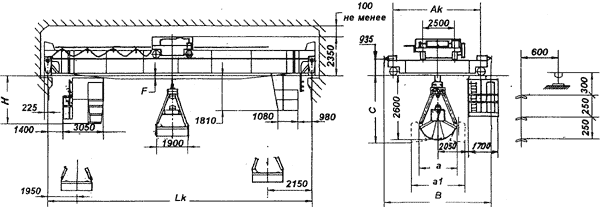
Характеристика
грузозахватного приспособления:
-
Грейферы для угля
1
2
Грузоподъемность крана, т
15
15
Вместимость грейфера, м3
5,6
6,5
Объемная масса груза max
кг/м31250
1250
Масса грейфера, кг
6020
6485
Габаритные размеры грейфера
Производительность
рассчитываться по формуле:
где
– расчетная производительность;
– время цикла;
– масса груза в одном подъеме.
Средневзвешенное
значение коэффициента заполнения
грейфера:
Так как уголь относится
к тяжелым грузам, то естественно
требуется соответствующий грейфер для
тяжелых навалочных грузов. Основное
отличие грейфера для тяжелых грузов
заключается в их большой массе по
отношению к массе полезного груза
перегружаемого за цикл крана или
перегружателя. Поэтому в среднем масса
полезного груза по отношению к
грузоподъемности крана составляет
всего 30-40%.
Подберём грейфер по загрузке
I слоя груза. Масса груза
в грейфере составит:
![]()
(для грейфера №1)
![]()
(для грейфера №2)
Как видно из расчета, грейфер № 2 поднимет
больше груза (5,94т). Собственная масса
грейфера равна 6,485т. Грузоподъемность
крана будет использована в большей
степени (12,425т).
Масса груза в грейфере
составит:
Слой I:
![]()
Слой II:
![]()
Определим возможные
варианты работ:
судно – склад
судно – вагон
склад – вагон
Технологический
процесс состоит из следующих операций:
кордонная – складская
кордонная – вагонная
складская – вагонная
Кордонная операция
осуществляется мостовым краном в
грейферном режиме. При работе на склад
тележка передвигается по эстакадам до
штабеля.
Складская операция
осуществляется мостовым краном в
грейферном режиме. Крановщик опускает
грузозахватное устройство с песком на
высоту 0,5 метра над уровнем склада и
осуществляет раскрытие. Крановщик
совмещает передвижение тележки вдоль
и поперёк крана.
Вагонная операция осуществляется
мостовым краном в грейферном. Крановщик
опускает грузозахватное устройство с
песком на высоту 0,5 метра над уровнем
вагона и осуществляет раскрытие.
Определим продолжительность
цикла на каждый вариант работ по следующей
аналитической формуле:
;
где t1
– время подъема груза и опускания
порожнего ГЗУ на среднюю высоту Hп;
t2
– время опускания груза и подъема
порожнего ГЗУ на среднюю высоту Hо;
t3
– время горизонтального перемещения
тележки (время перемещения тележки в
поперечном направлении не учитывается,
так как из-за больших габаритов груза
и относительного небольшого расстояния
перемещения поперечное перемещение
совмещается с продольным);
t4,
t6
– время установки порожнего ГЗУ на груз
и направление груженого ГЗУ на место
выгрузки;
t5
,t7
– время на захват груза и высыпание
его.
;
;
![]()
;
где Lср –
среднее расстояние перемещения груза
по варианту работ;
Vпередв –
скорость передвижения тележки = 1,47м/с;
Vп – скорость
подъема = 1,38 м/с.
Вместимость склада
![]()
=
133758т (если будем размещать весь груз
на одном причале).
Вместимость склада =
=
66879т (если будем размещать весь груз
на двух причалах).
Необходимый объем по расчётной емкости
склада:
Vрасч
=
/![]()
=
133758/1,1 =121598,18м3(если на одном
причале).
Vрасч
=
/
=
66879/1,1=60799,09м3(если на двух
причалах).
Разместим
груз на одном причале, тогда при количестве
штабелей = 4 объем одного штабеля =
121598,18/4 = 30399,545м3.
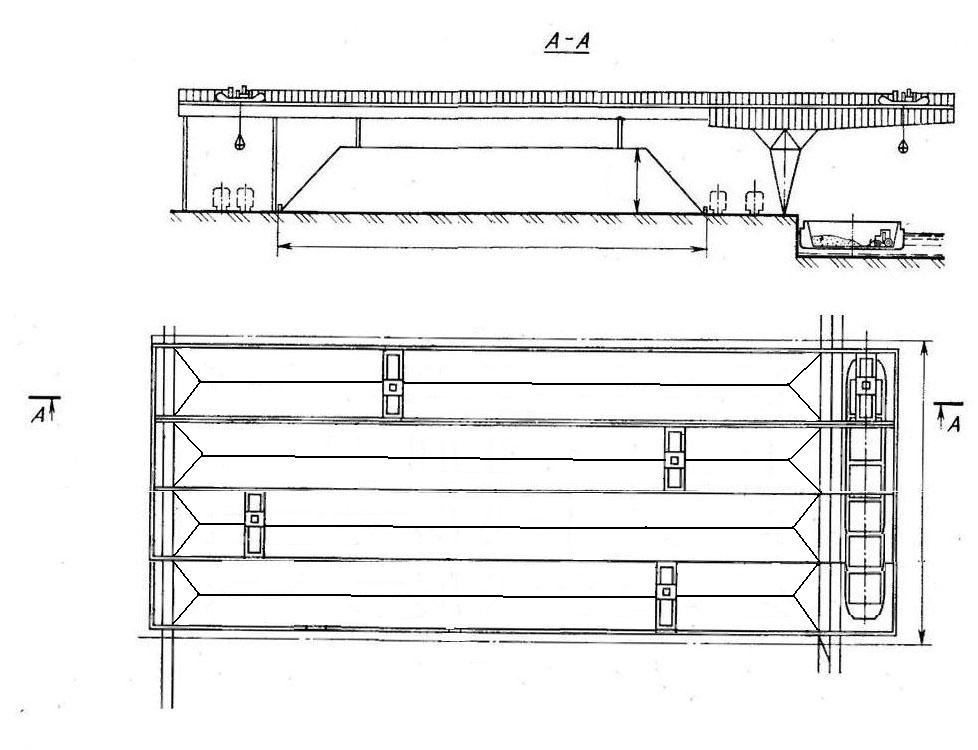
Открытый
склад для хранения угля будет представлять
собой клин (штабель между эстакадами
мостового крана):

![]()
Так как
длина каждого штабеля будет длиннее
52м (при В=26м,
![]()
),
высота штабелирования будет максимальная:
![]()
.
Для
нахождения Lшт
решим уравнение:

– коэффициент, учитывающий
совмещение операций:
судно – склад:
;
судно – вагон:
;
склад – вагон:
.
Для определения времени операций
необходимо определить высоту подъема
и опускания груза по каждому варианту
работ:
судно – склад:
![]()
;
.
судно – вагон:
![]()
.
склад – вагон:
так как
![]()
,
то
![]()
![]()
где
– осадка судна;
– средняя высота грузовых помещений;
– расстояние от причальной стенки до
уровня воды;
![]()
–
высота штабеля;
– высота вагона от уровня головок
рельса.
Lср
судно-склад
= (2,5+10,5+2,5+10,5+145,87)/2 = 85,94м;
Lср
судно-вагон
=2,5+10,5/2=7,75м;
Lср
склад-вагон
= 145,87/2 + 10,5/2 =78,19м.
Величины t4,
t5, t6,
t7 берутся
из нормативов на погрузо-разгрузочные
работы:
|
t4, |
t5, |
t6, |
t7, |
|
5 |
10 |
3 |
4 |
Определим
для каждого варианта работ:
судно – склад:
![]()
;
![]()
;
![]()
;
![]()
судно – вагон:
![]()
![]()
![]()
![]()
склад-вагон:
![]()
![]()
![]()
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
0 / 0 / 0 Регистрация: 02.10.2015 Сообщений: 1 |
|
|
1 |
|
Найдите высоту подъема груза02.10.2015, 17:47. Показов 3346. Ответов 1
При равноускоренном подъеме груза в течение времени t была совершена работа A. На какую высоту h был поднят груз, если его начальная скорость равна нулю и масса груза m?
0 |
|
480 / 327 / 32 Регистрация: 15.08.2011 Сообщений: 1,041 |
|
|
03.10.2015, 16:10 |
2 |
|
формулы для решения такие:
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
03.10.2015, 16:10 |
|
Помогаю со студенческими работами здесь Определить начальную скорость камня и высоту его подъема Найти высоту подъема шара и и угол отклонения стержня Найти время и высоту подъема стального шара, падающего на плиту Найти начальную скорость брошенного камня, время полета и максимальную высоту подъема.
Вычислить работу, совершаемую при равноускоренном поднятии груза на высоту за время. Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 2 |
Простые механизмы.
-
Рычаг.
-
Неподвижный блок.
-
Подвижный блок.
-
Наклонная плоскость.
-
Золотое правило механики.
-
КПД механизма.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.
Механизм – это приспособление для преобразования силы (её увеличения или уменьшения).
Простые механизмы – это рычаг и наклонная плоскость.
Рычаг.
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной оси. На рис. 1) изображён рычаг с осью вращения . К концам рычага (точкам
и
) приложены силы
и
. Плечи этих сил равны соответственно
и
.
Условие равновесия рычага даётся правилом моментов: , откуда
.
 |
| Рис. 1. Рычаг |
Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.
Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).
Примерами рычага, дающего выигрыш в силе, являются лопата, ножницы, плоскогубцы. Весло гребца – это рычаг, дающий выигрыш в расстоянии. А обычные рычажные весы являются равноплечим рычагом, не дающим выигрыша ни в расстоянии, ни в силе (в противном случае их можно использовать для обвешивания покупателей).
к оглавлению ▴
Неподвижный блок.
Важной разновидностью рычага является блок – укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.
На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).
 |
На правом конце нити в точке закреплён груз весом
. Напомним, что вес тела – это сила, с которой тело давит на опору или растягивает подвес. В данном случае вес
прило жен к точке
, в которой груз крепится к нити.
К левому концу нити в точке приложена сила
.
Плечо силы равно
, где
– радиус блока. Плечо веса
равно
. Значит, неподвижный блок является равноплечим рычагом и потому не даёт выигрыша ни в силе, ни в расстоянии: во-первых, имеем равенство
, а во-вторых, в процессе движении груза и нити перемещение точки
равно перемещению груза.
Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.
к оглавлению ▴
Подвижный блок.
На рис. 3 изображён подвижный блок, ось которого перемещается вместе с грузом. Мы тянем за нить с силой , которая приложена в точке
и направлена вверх. Блок вращается и при этом также движется вверх, поднимая груз, подвешенный на нити
.
 |
В данный момент времени неподвижной точкой является точка , и именно вокруг неё поворачивается блок (он бы “перекатывается” через точку
). Говорят ещё, что через точку
проходит мгновенная ось вращения блока (эта ось направлена перпендикулярно плоскости рисунка).
Вес груза приложен в точке
крепления груза к нити. Плечо силы
равно
.
А вот плечо силы , с которой мы тянем за нить, оказывается в два раза больше: оно равно
. Соответственно, условием равновесия груза является равенство
(что мы и видим на рис. 3: вектор
в два раза короче вектора
).
Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).
У блока на рис. 3 есть один недостаток: тянуть нить вверх (за точку ) – не самая лучшая идея. Согласитесь, что гораздо удобнее тянуть за нить вниз! Вот тут-то нас и выручает неподвижный блок.
 |
На рис. 4 изображён подъёмный механизм, который представляет собой комбинацию подвижного блока с неподвижным. К подвижному блоку подвешен груз, а трос дополнительно перекинут через неподвижный блок, что даёт возможность тянуть за трос вниз для подъёма груза вверх. Внешнее усилие на тросе снова обозначено вектором .
Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.
к оглавлению ▴
Наклонная плоскость.
Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.
В механике подобный механизм называется наклонной плоскостью. Наклонная плоскость – это ровная плоская поверхность, расположенная под некоторым углом к горизонту. В таком случае коротко говорят: “наклонная плоскость с углом
“.
Найдём силу, которую надо приложить к грузу массы , чтобы равномерно поднять его по гладкой наклонной плоскости с углом
. Эта сила
, разумеется, направлена вдоль наклонной плоскости (рис. 5).
 |
Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:
.
Проектируем на ось :
,
откуда
.
Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.
Чтобы равномерно поднимать тот же груз по вертикали, к нему нужно приложить силу, равную . Видно, что
, поскольку
. Наклонная плоскость действительно даёт выигрыш в силе, и тем больший, чем меньше угол
.
Широко применяемыми разновидностями наклонной плоскости являются клин и винт.
к оглавлению ▴
Золотое правило механики.
Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.
Например, рычаг с отношением плеч 2 : 1 даёт выигрыш в силе в два раза. Чтобы на меньшем плече поднять груз весом , нужно к большему плечу приложить силу
. Но для поднятия груза на высоту
большее плечо придётся опустить на
, и совершённая работа будет равна:
т. е. той же величине, что и без использования рычага.
В случае наклонной плоскости мы выигрываем в силе, так как прикладываем к грузу силу , меньшую силы тяжести. Однако, чтобы поднять груз на высоту
над начальным положением, нам нужно пройти путь
вдоль наклонной плоскости. При этом мы совершаем работу
т. е. ту же самую, что и при вертикальном поднятии груза.
Данные факты служат проявлениями так называемого золотого правила механики.
Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.
Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.
к оглавлению ▴
КПД механизма.
На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу Aполн,
которая совершается для тех же целей в реальной ситуации.
Полная работа равна сумме:
-полезной работы;
-работы, совершённой против сил трения в различных частях механизма;
-работы, совершённой по перемещению составных элементов механизма.
Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.
Полная работа всегда больше полезной. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:
=Aполезн/Аполн.
КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.
Вычислим КПД наклонной плоскости с углом при наличии трения. Коэффициент трения между поверхностью наклонной плоскости и грузом равен
.
Пусть груз массы равномерно поднимается вдоль наклонной плоскости под действием силы
из точки
в точку
на высоту
(рис. 6). В направлении, противоположном перемещению, на груз действует сила трения скольжения
.
 |
Ускорения нет, поэтому силы, действующие на груз, уравновешены:
.
Проектируем на ось X:
. (1)
Проектируем на ось Y:
. (2)
Кроме того,
, (3)
Из (2) имеем:
.
Тогда из (3):
.
Подставляя это в (1), получаем:
.
Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:
Aполн=.
Полезная работа, очевидно, равна:
Аполезн=.
Для искомого КПД получаем:
Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Простые механизмы.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Задачи на свободное падение тел: примеры решения задач по кинематике

Вторник, а это значит, что сегодня мы снова решаем задачи. На это раз, на тему «свободное падение тел».
Присоединяйтесь к нам в телеграм и получайте актуальную рассылку каждый день!
Задачи на свободное падение тел с решением
Задача №1. Нахождение скорости при свободном падении
Условие
Тело падает с высоты 20 метров. Какую скорость оно разовьет перед столкновением с Землей?
Решение
Высота нам известна по условию. Для решения применим формулу для скорости тела в момент падения и вычислим:

Ответ: примерно 20 метров в секунду.
Задача №2. Нахождение высоты и времени движения тела, брошенного вертикально.
Условие
Индеец выпускает стрелу из лука вертикально вверх с начальной скоростью 25 метров в секунду. За какое время стрела окажется в наивысшей точке и какой максимальной высоты она достигнет стрела?
Решение
Сначала запишем формулу из кинематики для скорости. Как известно, в наивысшей точке траектории скорость стрелы равна нулю:
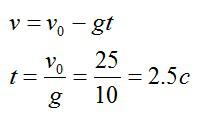
Теперь запишем закон движения для вертикальной оси, направленной вертикально вверх.
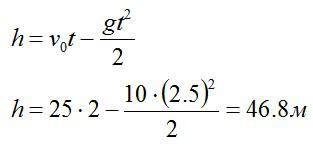
Ответ: 2,5 секунды, 46 метров.
Задача №3. Нахождение времени движения тела, брошенного вертикально вверх
Условие
Мячик бросили вертикально вверх с начальной скоростью 30 метров в секунду. Через какое время мяч окажется на высоте 25 метров?
Решение
Запишем уравнение для движения мячика:
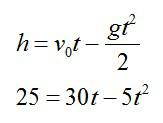
Мы получили квадратное уравнение. Упростим его и найдем корни:
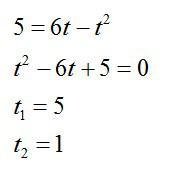
Как видим, уравнение имеет два решения. Первый раз мячик побывал на высоте через 1 секунду (когда поднимался), а второй раз через 5 секунд (когда падал обратно).
Ответ: 1с, 5с.
Задача №4. Нахождение высоты при движении тела под углом к горизонту
Условие
Камень, брошенный с крыши дома под углом альфа к горизонту, через время t1=0,5c достиг максимальной высоты, а еще через время t2=2,5c упал на землю. Определите высоту Н дома. Сопротивлением воздуха пренебречь. Ускорение свободного падения g = 10 м/с2.
Решение
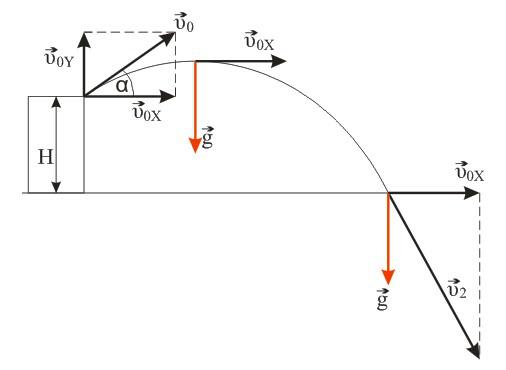
Камень брошен со скоростью v0 под углом α к горизонту с дома высотой Н. Эту скорость можно разложить на две составляющие: v0X (горизонтальная) и v0Y (вертикальная). В горизонтальном направлении на камень не действует никаких сил (сопротивлением воздуха пренебрегаем), поэтому горизонтальная составляющая скорости неизменна на протяжении всего времени полета камня (равномерное движение). Максимальная точка траектории камня над уровнем земли (исходя из кинематических соотношений):
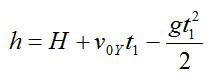
Здесь t1 – время подъема камня с высоты Н на высоту h; g – ускорение свободного падения.
Вертикальную составляющую скорости можно вычислить исходя из геометрических соображений:
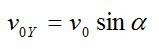
Подставив выражение для скорости в первое уравнение, получим:
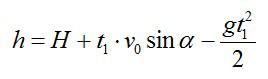
Также высоту h можно выразить через время t2 падения камня с высоты h на землю (исходя из кинематических соотношений и учитывая, что с вертикальная составляющая скорости в наивысшей точке равна нулю):
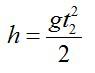
Для высоты дома можно записать:
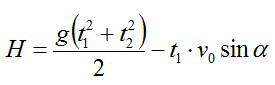
Так как вертикальная составляющая скорости камня в максимальной точке траектории равна нулю:
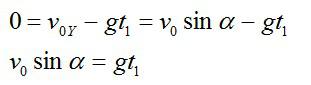
Подставляем в формулу для высоты H и вычисляем:
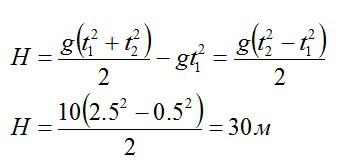
Ответ: H = 30 м.
Задача №5. Нахождение закона движения тела
Условие
Найти закон движения тела против силы тяжести, при начальной скорости V0. И на какую максимальную высоту поднимется тело? Тело бросили под углом 90 градусов.
Решение
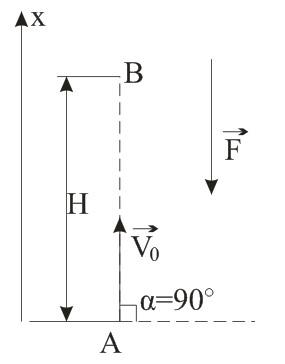
Тело брошено под углом α=90° к горизонту. Другими словами, тело брошено вертикально вверх с начальной скоростью V0. Направим координатную ось х вертикально вверх, так ее направление совпадает с вектором начальной скорости. F – сила тяжести, направленная вниз. В начальный момент тело находится в точке А.
В задаче нужно найти закон движения тела, то есть зависимость координаты тела от времени. В общем случае этот закон задается кинематическим соотношением:
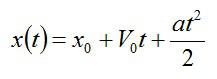
где х0 – начальная координата тела; a – ускорение.
Так как мы поместили начало координат в точку А, х0=0. Тело движется с ускорением свободного падения g, при этом сила тяжести направлена против начальной скорости, поэтому в проекции на вертикальную ось a=-g. Таким образом, искомый закон движения перепишется в виде:
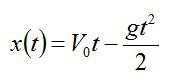
Далее будем использовать еще одно общее кинематическое соотношение:

где V – конечная скорость.
Максимальная высота подъема тела указана на рисунке точной B, в этот момент конечная скорость V равна нулю, а координата х равна максимальной высоте Н подъема тела. Отсюда можно найти выражение для этой величины:
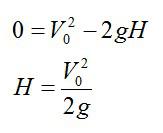
Полезные формулы для решения задач на свободное падение
Свободное падение описывается формулами кинематики. Мы не будем приводить их вывод, но запишем самые полезные.
Формула для максимальной высоты подъема тела, брошенного вертикально вверх c некоторой начальной скоростью:
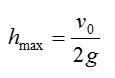
Кстати, как выводится именно эта формула можно посмотреть в последней задаче.
Формула для времени подъема и падения тела, брошенного вертикально вверх:

Скорость тела в момент падения с высоты h:
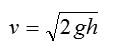
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Вопросы с ответами на свободное падение тел
Вопрос 1. Как направлен вектор ускорения свободного падения?
Ответ: можно просто сказать, что ускорение g направлено вниз. На самом деле, если говорить точнее, ускорение свободного падения направлено к центру Земли.
Вопрос 2. От чего зависит ускорение свободного падения?
Ответ: на Земле ускорение свободного падения зависит от географической широты, а также от высоты h подъема тела над поверхностью. На других планетах эта величина зависит от массы M и радиус R небесного тела. Общая формула для ускорения свободного падения:
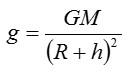
Вопрос 3. Тело бросают вертикально вверх. Как можно охарактеризовать это движение?
Ответ: В этом случае тело движется равноускоренно. Причем время подъема и время падения тела с максимальной высоты равны.
Вопрос 4. А если тело бросают не вверх, а горизонтально или под углом к горизонту. Какое это движение?
Ответ: можно сказать, что это тоже свободное падение. В данном случае движение нужно рассматривать относительно двух осей: вертикальной и горизонтальной. Относительно горизонтальной оси тело движется равномерно, а относительно вертикальной – равноускоренно с ускорением g.
Баллистика – наука, изучающая особенности и законы движения тел, брошенных под углом к горизонту.
Вопрос 5. Что значит «свободное» падение.
Ответ: в данном контексте понимается, что тело при падении свободно от сопротивления воздуха.
Свободное падение тел: определения, примеры
Свободное падение – равноускоренное движение, происходящее под действием силы тяжести.
Первые попытки систематизированно и количественно описать свободное падение тел относятся к средневековью. Правда, тогда было широко распространено заблуждение, что тела разной массы падают с разной скоростью. На самом деле, в этом есть доля правды, ведь в реальном мире на скорость падения сильно влияет сопротивление воздуха.
Однако, если им можно пренебречь, то скорость падающих тел разной массы будет одинакова. Кстати, скорость при свободном падении возрастает пропорционально времени падения.
Ускорение свободно падающих тел не зависит от их массы.
Примеры свободного падения тел:
- яблоко летит на голову Ньютона;
- парашютист выпрыгивает из самолета;
- перышко падает в герметичной трубке, из которой откачан воздух.
При свободном падении тела возникает состояние невесомости. Например, в таком же состоянии находятся предметы на космической станции, движущейся по орбите вокруг Земли. Можно сказать, что станция медленно, очень медленно падает на планету.
Конечно, свободное падение возможно не только не Земле, но и вблизи любого тела, обладающего достаточной массой. На других комических телах падения также будет равноускоренным, но величина ускорения свободного падения будет отличаться от земной. Кстати, раньше у нас уже выходил материал про гравитацию.
При решении задач ускорение g принято считать равным 9,81 м/с^2. В реальности его величина варьируется от 9,832 (на полюсах) до 9,78 (на экваторе). Такая разница обусловлена вращением Земли вокруг своей оси.
Нужна помощь в решении задач по физике? Обращайтесь в профессиональный студенческий сервис в любое время.
Падение тел
Свободное падение представляет собой частный случай равномерно ускоренного движения без начальной скорости. Ускорение этого движения равно ускорению свободного падения, называемого также ускорением силы тяжести. Для этого движения справедливы формулы:
u — скорость падения тела спустя время t
g — ускорение свободного падения, 9.81 (м/с?)
h — высота с которой падает тело
t — время, в течение которого продолжалось падение
- Сопротивление воздуха в данных формулах не учитывается.
- Ускорение свободного падения имеет приведенное значение (9.81 (м/с?)) вблизи земной поверхности. Значение g на других расстояниях от поверхности Земли изменяется!
Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением a = -g. Перемещение тела за время t представляет собой высоту подъема h.Для этого движения справедливы формулы:
U0 — начальная скорость движения тела
U — скорость падения тела спустя время t
g — ускорение свободного падения, 9.81 (м/с?)
h — высота на которую поднимется тело за время t
t — время
Скорость тела на некоторой высоте:
Максимальная высота подъёма тела:
Время подъёма на максимальную высоту:
Сложение движений, направленных под углом друг к другу.
Тело может одновременно участвовать в нескольких поступательных движениях. Поскольку ускорение, скорость и перемещение являются векторными величинами, их можно складывать по законам векторного (геометрического) сложения. Т.е. по правилу параллелограмма.
Величину результирующей любой характеристики движения можно вычислить.
Если:
Up — результирующая мгновенная скорость,
U1 — мгновенная скорость первого движения,
U2 — мгновенная скорость второго движения,
? — угол, образуемый векторами скоростей u1 и u2,
То по теореме косинусов получим:
Если движения 1 и 2 происходят под прямым углом друг к другу, то формула упрощается поскольку
Движение тела, брошенного горизонтально.
Движение тела, брошенного горизонтально, представляет собой комбинацию двух движений, взаимно перпендикулярных друг другу:
— горизонтального (равномерного) движения,
— вертикального (свободного падения)
Уравнение траектории тела, брошенного горизонтальн
Если построить траекторию движения тела, брошенного горизонтально, в системе координат xy, приняв за начало отсчета координат точку бросания, а направление оси ординат совпадающим с направлением вектора ускорения свободного падения, то координаты каждой точки траектории представляют собой перемещение тела в горизонтальном направлении (движение с постоянной скоростью U0) и в вертикальном направлении (равномерно ускоренное движение с ускорением g)
x, y — координаты тела,
u0 — начальная скорость тела (м/с),
g — ускорение свободного падения 9.81 (м/c2),
t — время движения (c)

Уравнение траектории тела, брошенного горизонтальновыглядит следующим образом:
Так как ускорение свободного падения g и начальная скорость тела u0 — постоянные величины, то координата yпропорциональна квадрату x, т.е. траектория движения представляет собой параболу, вершина которой находится в начальной точке движения.
Вектор положения тела брошенного горизонтально, формула
Положение каждой точки траектории тела брошенного горизонтально можно задать вектором положения r, который представляет собой результирующее перемещение:
или Вектор положения:
Координата по оси x:
Координата по оси y:
Примечание: Сопротивление воздуха в формулах не учитывается.
Уравнение движения тела, брошенного под углом к горизонту.
Координаты точки траектории описываются уравнениями:
x, y — координаты тела
U0 — начальная скорость тела (м/с)
? — угол, под которым брошено тело к горизонту (°)
g — ускорение свободного падения 9.81 (м/c2)
t — время движения (c)
Из формул через параметр t выводится общее уравнение движения тела, брошенного под углом к горизонту
Так как ускорение свободного падения g, ? — угол, под которым брошено тело к горизонту и начальная скорость тела u0 —постоянные величины, то координата y пропорциональна квадрату x, т.е. траектория движения представляет собой параболу, начальная точка находится на одной из ее ветвей, а вершина параболы, есть точка максимального подъема тела.
Время подъема на максимальную высоту, тела, брошенного под углом к горизонту.
Время подъема на максимальную высоту определяется из условия, что вертикальная составляющая мгновенной скорости равна нулю
из этого уравнения получаем:
U0 — начальная скорость тела (м/с),
? — угол, под которым брошено тело к горизонту (°),
g — ускорение свободного падения 9.81 (м/c2),
thmax — время подъема на максимальную высоту (c)
Дальность броска тела, брошенного под углом к горизонту.
Дальность броска или радиус поражения определяется по формулам общего времени движения и формулы координат тела
подставив tsmax в выражение и упростив получим:

U0 — начальная скорость тела (м/с),
? — угол, под которым брошено тело к горизонту (°),
g — ускорение свободного падения 9.81 (м/c2),
tsmax — общее время движения(c)
1.7. Свободное падение. Движение тела, брошенного вертикально вверх
[latexpage]Перейдем к рассмотрению частных видов равноускоренного движения. Отметим сразу, что все формулы, которые мы получили ранее для равноускоренного движения, будут верны и этих случаях. Начнем с движения, которое носит название — свободное падение. Под таким движением понимается движение с постоянным ускорением свободного падения, т.е. тогда, когда при движении тела можно пренебречь сопротивлением воздуха (понятно, что сопротивление воздуха при движении тел в атмосфере присутствует всегда, но в некоторых случаях его влияние не столь существенно по сравнению с действием силы притяжения). Помимо свободного падения мы будем рассматривать движение тела с постоянным ускорением свободного падения в случаях, когда тело:
а) брошено вертикально вверх;
б) брошено горизонтально;
в) брошено под углом к горизонту.
То есть все эти случаи объединяет то, что известно ускорение с которым движутся тела. Напомним, что модуль ускорения свободного падения равен 9,8 м/с 2 , однако, чаще всего, в задачах принимается $g approx 10$ м/с 2 , а направлен вектор ускорения свободного падения — вертикально вниз (хотя на самом деле нужно помнить, что вектор ускорения свободного падения направлен к центру Земли, это важно, например, при решении тех задач, когда тело вращается вокруг Земли, но ввиду того, что обычно движение тел происходит в масштабах не сопоставимых с размерами Земли, его изображают направленным вертикально вниз). Рассмотрим кинематику свободного падения.

Формулы, описывающие движение:
$v_x=v_+g_x t Rightarrow v=v_0+gt$,
Чаще всего в задачах встречаются формулировки при которых начальная скорость равна нулю (например, тело падает свободно, тело начинает падать, сосулька оторвалась от крыши и т.д.). Тогда вид формул значительно упрощается
В этом случае $H$ — высота с которой падает тело, а время падения можно найти так: $t=sqrt>$.
Движение тела, брошенного вертикально вверх. Заметим, что движение тела в этом случае можно разбить на два участка. На первом участке тело будет двигаться вверх, а на втором — свободно падать (тогда можно применять формулы написанные выше). Рассмотрим кинематику вертикального движения тела.

Формулы, описывающие движение:
$v_x=v_+g_x t Rightarrow v=v_0-gt$,
Заметим, что данные формул отличаются от предыдущих только знаком проекции ускорения.
Рассмотрим несколько примеров решения задач. При решении легких задач достаточно применение моделей, описанных выше и применение соответствующих формул. При решении задач более сложных задач, когда, например, происходит движение двух или более тел, будем придерживаться алгоритма, описанного нами в п. 1.6.1. Решение задач на равноускоренное движение. Алгоритм решения задач по кинематике. В дальнейшем, также, будем полагать, что сопротивлением воздуха можно пренебречь.
Пример. Мячик бросают вертикально вверх со скоростью 19,6 м/с. Через какое время мячик окажется: а) в наивысшей точке движения; б) в точке броска?
Решение. На первом участке движения мячик движется вертикально вверх, значит можем воспользоваться моделью, описанной нами выше, полагая, что $x_0=0$. Тогда движение мячика описывается формулами
Из формулы скорости найдем время подъема. Поскольку в наивысшей точке движения мяч остановится, то его скорость будет равна нулю
Значит, $t=frac=2$ с. Найдем и высоту подъема из формулы координаты для найденного момента времени $x=19,6cdot 2-frac=19,6$ м.
Теперь рассмотрим второй участок движения — на нем тело свободно падает без начальной скорости, а значит $t=sqrt>$, т.е.
Из этой задачи можно сделать важное наблюдение — если подбросить тело вертикально вверх, то время его подъема вверх будет равно времени его падения (на такую же высоту) вниз.
Пример. Свободно падающее тело в некоторый момент времени находилось на высоте 1100 м, а спустя 10 с — на высоте 120 м над поверхностью земли. С какой высоты падало тело?
Решение. Выполним чертеж. Систему отсчета свяжем с землей. Координатную ось направим вниз. Начало координат поместим в точку из которой тело начало движение.

Запишем уравнение движения в выбранной системе отсчета
Тело, с интервалом времени в 10 с, побывало в точках с координатами $x_1$ и $x_2$, причем $x_2-x_1=h_1-h_2$. Обозначим время движения тела до точки с координатой $x_1$ за $t$, а время которое прошло пока тело падало с высоты 1100 м на высоту 120 за $Delta t$, тогда
Найдем время движения до высоты 1100 м
или $x_2-x_1=gtDelta t+frac$. Выражаем из полученной формулы время
Найдем перемещение свободно падающего тела за 5 с
Тогда $h_0=s+h_1=122,5+1100=122,5$ м.
Пример. С воздушного шара, опускающегося вертикально вниз со скоростью 2 м/с, бросили вертикально вверх камень со скоростью 10 м/с относительно земли. Каким будет максимальное расстояние между шаром и камнем?
Решение. В данном типе задач особое внимание следует обратить на то, относительно чего задана скорость тела отделившегося от другого движущегося тела. В нашем случае обе скорости указаны относительно неподвижной системы отсчета, связанной с землей, что упрощает решение задачи (иначе бы вначале пришлось применять закон сложения скоростей). Выполним чертеж. Систему отсчета свяжем с землей. Координатную ось направим вертикально вверх. За начало координат примем точку в которой произошел бросок камня.

Движение первого тела — равномерное, значит его уравнение движения $x_1=x_0+v_t=-v_1 t$.
Движение второго тела — равноускоренное, известное нам уже движение тела, брошенного вертикально вверх с начальной скоростью $v_2=10$ м/с. Запишем уравнение координаты и скорости
$v_x=v_+g_x t Rightarrow v=v_2-gt$,
Согласно условию расстояние между телами должно быть максимальным. Это расстояние будет увеличиваться по мере того, как камень будет подниматься вверх, пока не остановится. После этого он начнет падать и расстояние между телами начнет сокращаться. Значит расстояние между телами будет максимально в тот момент времени, когда скорость камня станет равна нулю
$v_-g t =0Rightarrow t=frac$,
Координата первого тела в момент времени $t$
$x_1=-2 cdot 1,02=-2,04$ м.
Координата второго тела в момент времени $t$
$x_2=10 cdot 1,02 -frac approx 5,1$ м.
Искомое расстояние $l=x_2-x_1=5,1-(-2,04)=7,14$ м.
Пример. Тело, свободно падающее с некоторой высоты, первый участок пути проходит за время t1 = 4 с, а такой же последний — за время t2 = 2 с. Найдите высоту и время падения тела. Ускорение свободного падения примите равным 10 м/с 2 .
Решение. Выполним чертеж. Систему отсчета свяжем с землей. Координатную ось направим вниз. Начало координат поместим в точку из которой тело начало движение, т.е. $x_0=0$.

Так как тело свободно падает, то $v_0=0$. Значит координата имеет вид
По условию, за время 4 с и 2 с тело проходит одинаковые пути, найдем их
Поскольку нам известно время движения на последнем участке, то найдем время, через которое тело откажется в точке с координатой $x_2$, обозначим его через $t$, тогда
После преобразований (попробуйте выполнить их самостоятельно, подобно тому как это делалось выше), получим
Итого, общее время движения $t_o=t+t_2=3+2=5$ с.
Так как общее время меньше, чем сумма времен на заданных в условии участках, делаем вывод, что эти участки «пересекались». Таким образом, рисунок должен выглядеть следующим образом:

Но вид рисунка не имеет значения, не влияет на результат, а только помогает написать правильные уравнения.
Пример. С какой начальной скоростью нужно бросить вертикально вниз тело с высоты h = 39,2 м, чтобы оно упало на ∆t = 2 с быстрее тела, свободно падающее с этой высоты?
Решение. Выполним чертеж. Систему отсчета свяжем с землей. Координатную ось направим вниз. Начало координат поместим в точку из которой тела начали движение, т.е. $x_0=0$.

Запишем уравнения движения для первого и второго тела соответственно
Из второго уравнения, учитывая, что в момент падения $x_1=h$, найдем время движения второго тела
Значит, время движения первого тела $t_1=t_2-Delta t=0,8$ с. Из уравнения движения выразим начальную скорость
Пример. Тело начинает падать с высоты $H=45$ м. В тот же момент из точки, расположенной на высоте $h=24$ м, бросают другое тело вертикально вверх. Оба тела падают на землю одновременно. Определить начальную скорость второго тела, приняв ускорение свободного падения равным 10 м/с 2 .
Решение. Выполним чертеж. Систему отсчета свяжем с землей. Координатную ось направим вниз. Начало координат поместим в точку из которой тела начинает свободно падать.

Уравнения движения первого и второго тела соответственно, учитывая, что начальная координата движения второго тела равна $x_=H-h$
Из первого уравнения найдем время, в течении которого тела движутся, учитывая, что в момент падения $x_=H$
Так как в момент падения второго тела его координата также будет равна $H$, а время движения также составляет 3 с, получим
Пример. С воздушного шара, опускающегося с постоянной скоростью 4 м/с, бросили вертикально вверх груз со скоростью u = 20 м/с относительно шара. Определите расстояние между грузом и шаром в тот момент, когда груз достигает высшей точки подъема. Спустя какое время после броска груз пролетит мимо шара? Ускорение свободного падения равно 10 м/с 2 .
Решение. Выполним чертеж. Систему отсчета свяжем с землей. Координатную ось направим вниз. Начало координат поместим в точку где происходит бросок камня.

В условии задачи сказано, что скорость груза указана относительно шара, т.е. движущейся системы отсчета (относительно неподвижной, выбранной нами, системы отсчета — земли). Применим закон сложения скоростей:
- $overrightarrow$ — скорость тела относительно движущейся системы отсчета (относительно шара);
- $overrightarrow$ — скорость движущейся системы отсчета относительно неподвижной системы отсчета (шара относительно земли);
- $overrightarrow$ — скорость тела в неподвижной системе отсчета, она же начальная скорость при вертикальном движении тела вверх.
Напишем уравнения движения, учитывая, что первое тело движется равномерно, а второе тело — движется вертикально вверх и начальные координаты у них равны нулю
$x_1=v_t Rightarrow x_1=v_1 t$,
В момент времени, когда груз будет пролетать мимо шара их координаты будут равны, а значит
Теперь найдем расстояние между телами в момент времени, когда груз будет находиться в наивысшей точке подъема. Скорость груза определяется уравнением
$v_x=v_+g_x t Rightarrow v_x=u_x+v__g_x t = v_1-u+gt$.
В наивысшей точке подъема скорость груза будет равна нулю, значит время подъема
$ v_1-u+gt=0 Rightarrow t= frac$,
Расстояние между телами можно определить как разницу координат между телами в интересующий нас момент времени
$l=left | x_1 — x_2 right |= left | v_1 t- (v_1-u)t-fracright |=left |ut- fracright |$,
Задачи для самостоятельного решения.
1. С крыши дома оторвалась сосулька и за 0,2 с пролетела мимо окна, высота которого 1,5 м. С какой высот относительно верхнего конца окна она оторвалась? Размерами сосульки пренебречь.
2. Мячик, отскочивший от поверхности земли со скоростью 10 м/с, пролетел мимо окна, высота которого 1,5 м, за время 0,2 с. На какой высоте относительно земли находится подоконник?
3. Тело брошено вертикально вверх со скоростью v0 = 19,6 м/с. Сколько времени оно будет находиться на высоте, большей h = 14,7 м?
3. С вертолета, находящегося на высоте h = 300 м, сброшен груз. Спустя какое время груз достигнет земли, если вертолет: а) неподвижен; б) опускается со скоростью v = 5 м/с; в) поднимается со скоростью v = 5 м/с?
а) 7,8 с; б) 7,3 с; в) 8,3 с.
4. Одно тело свободно падает с высоты h = 392 м. Одновременно другое тело брошено с земли вертикально вверх со скоростью v = 78,4 м/с. Когда и на какой высоте тела встретятся?
5. Два парашютиста сделали затяжной прыжок с одной и той же высоты, один вслед за другим через t = 6 с. В какой момент времени, считая от прыжка первого парашютиста, расстояние между ними по вертикали будет h = 294 м?
6. Парашютист, спускающийся равномерно со скоростью v = 5 м/с в момент, когда находится на высоте H = 100 м над поверхностью земли, бросил вертикально вниз небольшое тело со скоростью v0 = 10 м/с относительно себя. Какой промежуток времени разделяет моменты приземления тела и парашютиста?
7. Аэростат поднимается вверх с ускорением 2 м/с2. Через 5 с от начала его движения из него выпадает предмет. Через сколько времени предмет упадет на землю?
8. Ракета стартует и движется вертикально вверх 20 с с ускорением $a=2g$. Через 20 с двигатели ракеты отключаются. Через какое время с момента старта ракета упадет на землю?
9. С каким промежутком времени оторвались две капли от крыши, если спустя 2 с после начала движения второй капли расстояние между ними было 25 м?
Как найти высоту, если знаешь массу предмета? Без сопротивления ветра. Сколько метров в секунду?
Temirlan Kazmukhamedov
23 июня 2018 · 16,1 K
Инженер-физик, IT-специалист, музыкант самоучка · 23 июн 2018
Задавайте вопросы корректней, т.к. нет точно поставленной цели. Найти высоту чего? Высоты на которую подбрасывают тело, с которой падает тела либо же оно скатывается по наклонной поверхности, высоту самого тела. Предположу что тело сбрасывают вниз без начального ускорения. В данном случае можем воспользоватся формулой H = (g*t^2) / 2. Где H – искомая высота g-ускорение свободного падения равное 9.8 м/c^2 t-время падения. Тогда скорость сможем рассчитать по формуле V=g*t. Но масса в данном случае нас не интересует так как мы не учитываем сопротивление воздуха. В любом случае учитесь задавать вопросы грамотно и корректно.
16,8 K
Высота разницы не имеет. Даже подбросив упадёт вниз, предполагаешь верно но на вопрос не ответил. Задам вопрос… Читать дальше
Комментировать ответ…Комментировать…

 На какую максимальную высоту поднимется оставшаяся часть груза
На какую максимальную высоту поднимется оставшаяся часть груза