Как найти высоту полученного тела вращения конуса

Как найти высоту конуса. Теория и формулы

Прочитав данную статью, вы узнаете, как найти высоту конуса. Приведенный в ней материал поможет глубже разобраться в вопросе, а формулы окажутся весьма полезными в решении задач. В тексте разобраны все необходимые базовые понятия и свойства, которые обязательно пригодятся на практике.

Фундаментальная теория

Перед тем, как найти высоту конуса, необходимо разобраться с теорией.

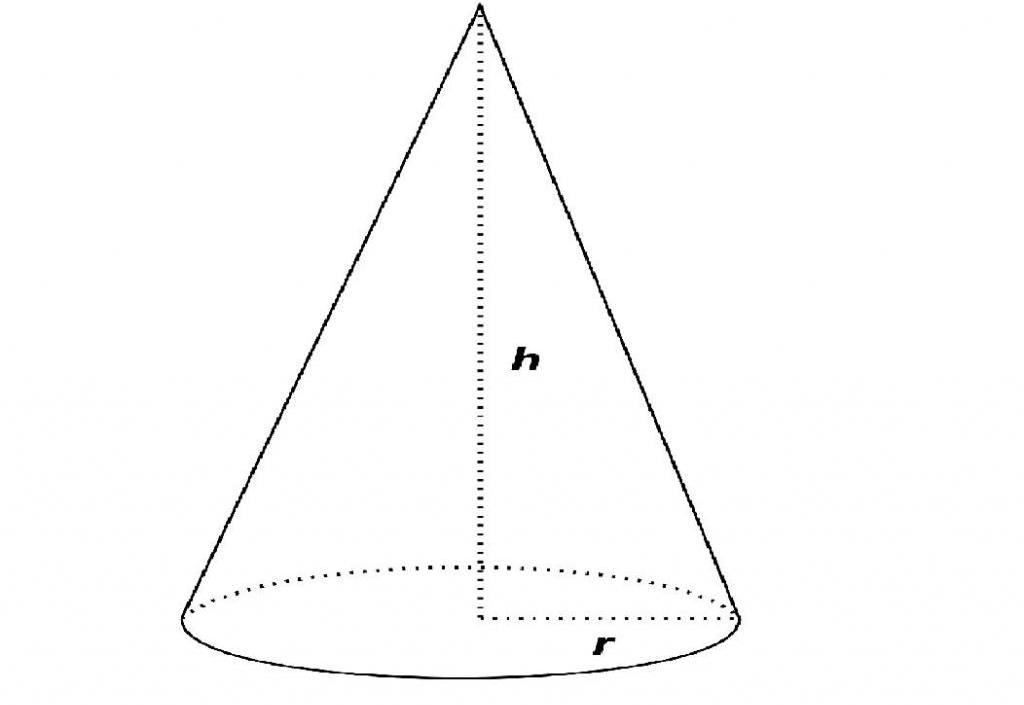
Конус – фигура, которая плавно сужается от плоского основания (часто, хотя и необязательно, кругового) до точки, называемой вершиной.

Конус формируется набором отрезков, лучей или прямых, соединяющих общую точку с основанием. Последнее может ограничиваться не только окружностью, но и эллипсом, параболой или гиперболой.

Ось – это прямая (если таковая имеется), вокруг которой фигура имеет круговую симметрию. Если угол между осью и основой составляет девяносто градусов, то конус принято называть прямым. Именно такая вариация чаще всего встречается в задачах.

Если в основе лежит многоугольник, то объект является пирамидой.

Отрезок, соединяющий вершину и линию, ограничивающую основание, называют образующей.

Как найти высоту конуса

Подойдем к вопросу с другой стороны. Для начала используем объем конуса. Чтобы его найти нужно вычислить произведение высоты с третьей частью площади.

Очевидно, что из этого можно получить формулу высоты конуса. Достаточно лишь сделать правильные алгебраические преобразования. Разделим обе части равенства на S и умножим на тройку. Получим:

Теперь вы знаете, как найти высоту конуса. Однако для решения задач вам могут понадобиться и другие знания.

Важные формулы и свойства

Приведенный ниже материал однозначно поможет вам в решении конкретных задач.

Центр массы тела находится на четвертой части оси, начиная от основы.

В проективной геометрии цилиндр – это просто конус, вершина которого находится на бесконечности.

Следующие свойства работают только для прямого кругового конуса.

• Даны радиус основания r и высота h, тогда формула для площади будет выглядеть так: П × r 2 . Соответственно изменится и окончательное уравнение. V = 1/3 × П × r 2 × h.
• Вычислить площадь боковой поверхности можно перемножив число “пи”, радиус и длину образующей. S = П × r × l.
• Пересечение произвольной плоскости с фигурой является одним из конических сечений.

Часто встречаются задачи, где необходимо использовать формулу для объема усеченного конуса. Она выводится из обычной и имеет такой вид:

V = 1/3 × П × h × (R 2 + Rr + r 2 ), где: r -радиус нижнего основания, R – верхнего.

Всего этого будет вполне достаточно для решения разнообразнейших примеров. Разве что могут понадобиться знания, не связанные с этой темой, например, свойства углов, теорема Пифагора и другое.

Радиус и высота конуса

Свойства

Через радиус конуса можно найти все параметры конуса, связанные с основанием, а значение высоты позволяет вычислить площади, объемы и все остальные объемные параметры конуса. Так, диаметр конуса равен удвоенному радиусу, периметр окружности в основании вычисляется по стандартной формуле через радиус, равно как и площадь основания. d=2r P=2πr S_(осн.)=πr^2

Прямоугольный треугольник, образованный высотой конуса, радиусом основания и образующей конуса, связывает эти три значения теоремой Пифагора, по которой можно вычислить неизвестную образующую, а также угол между образующей и основанием. Тем временем, угол α рассчитывается из равнобедренного треугольника, сформированного двумя образующими и диаметром из того принципа, что сумма всех углов в треугольнике равна 180 градусам. (рис.40.1, 40.2) l=√(h^2+r^2 ) tan⁡β=h/r α=180°-2β

Чтобы найти площадь боковой поверхности конуса, необходимо умножить радиус и апофему на число π. Площадь полной поверхности конуса состоит из площади его основания и площади боковой поверхности. В обеих формулах вместо апофемы нужно подставить квадратный корень через высоту и радиус, полученный по теореме Пифагора. S_(б.п.)=πrl=πr√(h^2+r^2 ) S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)=πr(√(h^2+r^2 )+r)

Чтобы найти объем конуса, достаточно знать значения радиуса и высоты, тогда формула объема выглядит как произведение числа π на квадрат радиуса и высоту, деленное на три. V=1/3 S_(осн.) h=(πr^2 h)/3

Радиус сферы, вписанной в конус, зависит не только от радиуса основания конуса и его высоты, но и от образующей, поэтому чтобы вычислить радиус вписанной сферы конуса через радиус конуса и высоту, нужно вместо образующей подставить полученное для нее выше выражение. Радиус описанной сферы может быть представлен сразу формулой только с переменными радиуса и высоты. (рис.40.3, 40.4) r_1=hr/(l+r)=rh/(√(h^2+r^2 )+r) R=(h^2+r^2)/2h

Как найти высоту конуса если известен объем

Прочитав данную статью, вы узнаете, как найти высоту конуса. Приведенный в ней материал поможет глубже разобраться в вопросе, а формулы окажутся весьма полезными в решении задач. В тексте разобраны все необходимые базовые понятия и свойства, которые обязательно пригодятся на практике.

Фундаментальная теория

Перед тем, как найти высоту конуса, необходимо разобраться с теорией.

Конус – фигура, которая плавно сужается от плоского основания (часто, хотя и необязательно, кругового) до точки, называемой вершиной.

Конус формируется набором отрезков, лучей или прямых, соединяющих общую точку с основанием. Последнее может ограничиваться не только окружностью, но и эллипсом, параболой или гиперболой.

Ось – это прямая (если таковая имеется), вокруг которой фигура имеет круговую симметрию. Если угол между осью и основой составляет девяносто градусов, то конус принято называть прямым. Именно такая вариация чаще всего встречается в задачах.

Если в основе лежит многоугольник, то объект является пирамидой.

Отрезок, соединяющий вершину и линию, ограничивающую основание, называют образующей.

Как найти высоту конуса

Подойдем к вопросу с другой стороны. Для начала используем объем конуса. Чтобы его найти нужно вычислить произведение высоты с третьей частью площади.

Очевидно, что из этого можно получить формулу высоты конуса. Достаточно лишь сделать правильные алгебраические преобразования. Разделим обе части равенства на S и умножим на тройку. Получим:

Теперь вы знаете, как найти высоту конуса. Однако для решения задач вам могут понадобиться и другие знания.

Важные формулы и свойства

Приведенный ниже материал однозначно поможет вам в решении конкретных задач.

Центр массы тела находится на четвертой части оси, начиная от основы.

В проективной геометрии цилиндр – это просто конус, вершина которого находится на бесконечности.

Следующие свойства работают только для прямого кругового конуса.

• Даны радиус основания r и высота h, тогда формула для площади будет выглядеть так: П × r 2 . Соответственно изменится и окончательное уравнение. V = 1/3 × П × r 2 × h.
• Вычислить площадь боковой поверхности можно перемножив число “пи”, радиус и длину образующей. S = П × r × l.
• Пересечение произвольной плоскости с фигурой является одним из конических сечений.

Часто встречаются задачи, где необходимо использовать формулу для объема усеченного конуса. Она выводится из обычной и имеет такой вид:

V = 1/3 × П × h × (R 2 + Rr + r 2 ), где: r -радиус нижнего основания, R – верхнего.

Всего этого будет вполне достаточно для решения разнообразнейших примеров. Разве что могут понадобиться знания, не связанные с этой темой, например, свойства углов, теорема Пифагора и другое.

Конус — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной

точки (вершины конуса) и проходящих через плоскую поверхность.

Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением

всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае

называют основанием конуса, а конус называют опирающимся на данное основание).

Воспользуйтесь онлайн калькулятором для расчета объема пирамиды: объем конуса, онлайн расчет.

Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.

• Отрезок, соединяющий вершину и границу основания, называется образующей конуса.

• Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.

Образующая поверхность конуса является конической поверхностью.

• Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого

отрезка), называется высотой конуса.

• Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине

конуса, внутри конуса).

• Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и

ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то

конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется

осью конуса.

• Косой (наклонный) конус — конус, у которого ортогональная проекция вершины на основание не

совпадает с его центром симметрии.

• Круговой конус — конус, основание которого является кругом.

• Прямой круговой конус (часто его называют просто конусом) можно получить вращением

прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось

• Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно

эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный

• Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся

между вершиной и основанием, называется усечённым конусом, или коническим слоем.

Объем конуса вычисляется по формуле:

где R — радиус основания конуса,

Усеченный конус.

Усеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело

ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом.

Объем усеченного конуса вычисляется по формуле:

h – высота конуса

r – радиус верхнего основания

R – радиус нижнего основания

или по формуле объема усечённого конуса (не обязательно прямого и кругового):

S1 и S2 — площади соответственно верхнего (ближнего к вершине) и нижнего оснований,

h и H — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.

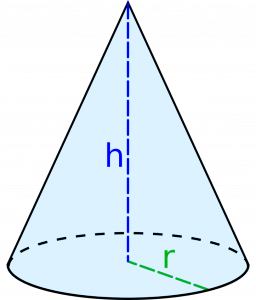
Конус — это трехмерная фигура, в основании которой лежит круг. Чтобы найти объем конуса достаточно знать два параметра — высоту (h) и радиус основания (r).

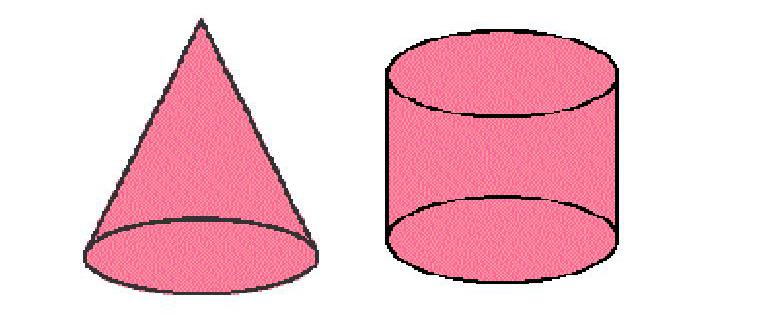
Если мы сравним формулу объема конуса с формулой объема цилиндра, то мы увидим, что объем конуса в 3 раза меньше объема цилиндра с той же высотой и радиусом основания.

Нахождение объема конуса, формула объема конуса

Подставив значения в формулу, можно легко найти объем:

[spoiler title=”источники:”]

http://geleot.ru/education/math/geometry/calc/cone/radius_and_height

http://4systems.ru/inf/kak-najti-vysotu-konusa-esli-izvesten-obem/

[/spoiler]

Длина отрезка линии опушенной перпендикулярно плоскости основания из вершины конуса является его высотой. Найти не сложно. Для этого нужно знать величину конуса. Если конус велик и внутри его полость, то достаточно опустить из вершины нитку с грузом до основания и измерить длину нитки. Если конус мал и умещается в руках, то достаточно измерить боковую сторону и ширину основания. Половина основания – это один катет. Боковая сторона гипотенуза. А высотой окажется другой катет воображаемого прямоугольного треугольника. К сожалению тут нарисовать не где. Далее, зная значения катета и гипотенузы по теореме Пифагора находим другой катет – высоту конуса. Если конус не симметричный и вершина сдвинута относительно середины, то для расчетов нужно знать угол между плоскостью основания и боковой стороной в месте их измерения. Далее геометрия… Формулы есть в любом справочнике. автор вопроса выбрал этот ответ лучшим Ксарф­акс [156K] 5 лет назад  Высота конуса Это перпендикуляр, который опущен из вершины конуса на основание. Чтобы найти высоту конуса можно воспользоваться несколькими способами. 1) Если известно, чему равен объём конуса, то высоту можно вычислить по формуле: V = 1/3 Sосн * h -> h = 3V / Sосн. При этом для нахождения площади основания (площади круга) нам нужно знать радиус. 2) Образующая конуса, высота и радиус основания образуют прямоугольный треугольник. Поэтому если известна образующая (гипотенуза) и радиус (катет), то высоту можно выразить с помощью теоремы Пифагора. a² = c² – b², a = √(c² – b²). a – высота, b – радиус, c – образующая. Например: Радиус основания = 15 см, длина образующей – 17 см. Высота конуса будет равна √(17² – 15²) = √64 = 8 см. -Irink­a- [281K] 4 года назад  Для того, чтобы найти высоту конуса, необходимо иметь для решения какие-то вводные. Допустим, что мы знаем длина образующей конуса, она равна 10 см. и диаметр его основания равный 12 см. Находим радиус конуса R=D/2= 6 см. Вот наш конус, чертим нужные нам линии. Используем теорему Пифагора, получаем h²=a²-R², где а – длина образующей конуса (10 см), h искомая высота. h² = 100 – 36 = 64 h = √64 = 8 сантиметров Alexg­roovy [14.6K] 5 лет назад  Для поиска высоты конуса нужны входные данные. В качестве таких данных выступает радиус (или диаметр основания) и длина образующей конуса. На рисунке длина образующей обозначена буквой l, а диаметр основания как d. Например, по условию задачи l = 100, d = 56. Решение задачи будет следующим: 88Sky­Walke­r88 [428K] 5 лет назад  Начертим конус, проведем его высоту и основание: Нам известна величина l – это образующая. Она равна 16. Угол между основанием и образующий будет равняться 30 градусам. У нас получился прямоугольный треугольник, в котором образующая (l) – это гипотенуза, а высота (h), которую нам необходимо найти, это катет. Так как нам известен угол, мы можем найти его синус. sin 30° = ½ Известно, что синус – это отношение противолежащего катета к гипотенузе. Следовательно, можно составить такую формулу: sin 30° = h/l = ½ Из этой формулы мы выводим h, высоту конуса. Получается формула и решение: h = sin 30°*l = ½ * 16 = 8. Чосик [208K] более года назад  Зависит от данных, которые мы получили изначально. Для того, чтобы узнать высоту, необходимо знать радиус и апофему. В таком случае мы получим прямоугольный треугольник, где высота и радиус играют роль катетов, а апофема – гипотенузы. Если же мы знает площадь основания и объем конуса, то высота равна h = 3V/S. владс­андро­вич [766K] более года назад  Высоту конуса можно найти разными формулами, тут все зависит от того, что вам известно. В частности если известны площадь его основания и объем самого конуса, то тогда все просто, так как данные значения надо подставить под формулу h = 3V/S и просто посчитать. JuliG­or [3.2K] 9 лет назад  Если известны объем и площадь конуса, то высоту легко найти, так как объем конуса равен одной трети площади основания умноженная на высоту конуса. Также высоту конуса можно найти по теореме Пифагора, но это по-моему гораздо сложнее) morel­juba [62.5K] 5 лет назад  Высоту конуса мы можем выразить из формулы, по которой мы определяем объём конуса: Так вот высота конуса из данной формулы будет равна: Высота конуса = 3 * объём конуса / пи * радиус основания в квадрате. Знаете ответ?

Геометрия, 11 класс

Урок №7. Конус

Перечень вопросов, рассматриваемых в теме:

• коническая поверхность, образующая конической поверхности, её вершина, ось;
• конус, основание конуса, вершина конуса, образующие конуса, ось конуса, высота конуса;
• боковая поверхность конуса, полная поверхность конуса;
• сечение конуса и его виды;
• усечённый конус и его элементы.
• площади поверхностей усеченного конуса.

Глоссарий по теме

Коническая поверхность – это поверхность, образованная прямыми, проходящими через все точки окружности, и точку, не лежащую в плоскости этой окружности.

Эти прямые – образующие конической поверхности.

Прямая, проходящая через центр окружности, перпендикулярно к плоскости – ось конической поверхности.

Конус– тело, ограниченное конической поверхностью, точкой и кругом.

Круг – основание конуса; точка – вершина конуса, отрезки образующих, заключённые между основанием и вершиной – образующие конуса; образованная ими часть конической поверхности – боковая поверхность конуса.

Ось конической поверхности называется осью цилиндра.

Расстояние от вершины до основания конуса называется высотой конуса, а радиус основания – радиусом конуса.

Сечение – изображение фигуры, образованной рассечением тела плоскостью.

Осевое сечение – вариант сечения, при котором плоскость проходит через ось тела.

Развёртка боковой поверхности конуса – сектор, радиус которого – образующая конуса, а длина дуги – длина окружности основания конуса.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 130-133.

Дополнительная литература:

Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. Учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-79.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

1. Основные определения

В плоскости 𝛂 построю окружность L с центром в точке О. Проведу прямую ОР перпендикулярно плоскости 𝛂. Соединю точку Р со всеми точками окружности L прямыми линиями. Поверхность, состоящую из этих прямых, называют конической поверхностью, сами прямые называют образующими конической поверхности, точку Р называют вершиной, а прямую ОР – осью конической поверхности.

Ввожу новые понятия конуса, основания конуса, вершины конуса, образующих конуса, боковой поверхности конуса, оси конуса и высоты конуса.

Определение

Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом.

Определение

Круг называют основанием конуса.

Определение

Вершину конической поверхности называют вершиной конуса.

Определение

Отрезки образующих, заключённые между вершиной и основанием называют образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса.

Определение

Ось конической поверхности называют и осью конуса, а её отрезок, заключённый между вершиной и основанием называют высотой конуса.

Отмечу, что все образующие конуса равны друг другу. Это легко доказать, если рассмотреть различные прямоугольные треугольники, в которых один катет – это высота конуса, а вторыми катетами являются радиусы основания конуса. Тогда образующие, являясь гипотенузами этих прямоугольных треугольников с равными катетами, также будут равны.

Конус можно получить ещё одним способом – вращением прямоугольного треугольника вокруг одного из катетов. Тогда этот катет (вокруг которого происходит вращение) будет совпадать с осью конуса и будет его высотой, гипотенуза станет образующей и будет образовывать боковую поверхность, а оставшийся катет образует основание, одновременно являясь его радиусом.

2. Сечения конуса различными плоскостями

1. Пусть секущая плоскость проходит через ось конуса. Такое сечение называют осевым. Оно представляет собой равнобедренный треугольник, боковые стороны которого – образующие конуса, а его основанием является диаметр основания конуса.

1. Если секущая плоскость перпендикулярна оси конуса, то сечение представляет собой круг с центром, расположенном на оси.

Это два основных вида сечения конуса, которые изучаются в средней школе на базовом уровне. Следует упомянуть, что существуют и другие сечения конусов, вид которых зависит от расположения секущей плоскости относительно оси.

3. Основные формулы

Формула для вычисления площади боковой поверхности конуса: S_бок=𝛑RL.

Площадь полной поверхности конуса: S_полн=𝛑R(R+L).

4. Усеченный конус

Если взять произвольный конус и провести секущую плоскость перпендикулярно его оси, то исходный конус разделится на две части. Верхняя часть представляет собой конус меньших размеров, а оставшуюся часть называют усечённым конусом.

Определение

Основание исходного конуса и круг, получившийся в сечении, называют основаниями усечённого конуса.

Определение

Отрезок, соединяющий центры оснований, называют высотой усечённого конуса.

Определение

Часть конической поверхности, ограничивающая усечённый конус, называется боковой поверхностью усечённого конуса.

Определение

Отрезки образующих, заключённые между основаниями, называются образующими усечённого конуса. Отмечу, что все образующие усечённого конуса равны друг другу.

Усечённый конус можно получить ещё одним способом – вращением прямоугольной трапеции вокруг той боковой стороны, которая перпендикулярна основанию.

Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью конуса и будет его высотой, другая боковая сторона станет образующей и при вращении будет образовывать боковую поверхность, а основания трапеции станут соответственно радиусами верхнего и нижнего оснований усечённого конуса.

5. Формула для вычисления площадей поверхностей усеченного конуса

S_{бок.пов.ук}=π(r+R)L

S_{.полн.пов.ук}=π(rL+RL+r²+R²)

Примеры и разбор решения заданий тренировочного модуля

1. Найти высоту конуса, если площадь его осевого сечения равна 6, а площадь основания равна 8.

Решение:

Сделаем чертеж:

S_ABC=6.

Его высота SO является высотой конуса.

S_ABC=SO·OB.

OB – радиус основания.

Его найдем из равенства: S_осн=πR².

8= πR².

R===OB.

Теперь найдем высоту:

6=SO·OB=SO·.

Отсюда: SO=3

Ответ: 3.

2. Прямоугольная трапеция с основаниями 4 и 7 и меньшей боковой стороной 4 вращается вокруг меньшей стороны. Найдите элементы усеченного конуса.

Величина

Высота конуса

Образующая конуса

Радиус меньшего основания

Радиус большего основания

Площадь боковой поверхности конуса

Площадь осевого сечения

Площадь полной поверхности конуса

Решение:

Сделаем чертеж:

Трапеция ABCD вращается вокруг стороны AD.

Тогда:

AD – высота усеченного конуса, AD=4.

АВ – радиус меньшего основания, AB=4.

DC – радиус большего основания, DC=7.

Площадь боковой поверхности конуса вычислим по формуле: S_{бок.пов.ук}=π(r+R)L.

Для того чтобы найти площадь боковой поверхности, нужно найти образующую.

Ее найдем из треугольника BHC: BC=5 (это египетский треугольник).

Теперь найдем площадь боковой поверхности.

S_б.п. =π(4+7)·5=55π.

Площадь боковой поверхности равна 55π.

Осевое сечение представляет собой равнобедренную трапецию с основаниями 8 и 14 и высотой, равной 4.

Так что площадь этой трапеции равна: S=4(4+7)=44.

Для того чтобы найти площадь полной поверхности, нужно к площади боковой поверхности прибавить площади ее оснований.

S_п.п.=55π+16π+49π=120π.

Величина	Значение
Высота конуса	4
Образующая конуса	5
Радиус меньшего основания	4
Радиус большего основания	7
Площадь боковой поверхности конуса	55π
Площадь осевого сечения	44
Площадь полной поверхности конуса	120π

§ 18. Конус

18.1.Определение конуса и его элементов

Определение. Тело, которое образуется при вращении прямоугольного треугольника вокруг прямой, содержащей его катет, называется прямым круговым конусом (рис. 165, 166).

Отрезок оси вращения, заключённый внутри конуса, называется осью конуса.

Круг, образованный при вращении второго катета, называется основанием конуса. Длина этого катета называется радиусом основания конуса или, короче, радиусом конуса. Вершина острого угла вращающегося треугольника, лежащая на оси вращения, называется вершиной конуса. На рисунках 165, б и 166 вершиной конуса является точка Р.

Высотой конуса называется отрезок, проведённый из вершины конуса перпендикулярно его основанию. Длину этого перпендикуляра также называют высотой конуса. Высота конуса имеет своим основанием центр круга — основания конуса — и совпадает с осью конуса.

Отрезки, соединяющие вершину конуса с точками окружности его основания, называются образующими конуса. Все образующие конуса равны между собой (почему?).

Как и в случае с цилиндром, можно рассматривать конус в более широком, чем у нас, понимании, когда в основании конуса может быть, например, эллипс (эллиптический конус), парабола (параболический конус). Мы будем изучать только определённый выше прямой круговой конус (конус вращения), поэтому слова «прямой круговой» мы будем опускать.

Поверхность, полученная при вращении гипотенузы, называется боковой поверхностью конуса, а её площадь — площадью боковой поверхности конуса и обозначается Sбок. Боковая поверхность конуса является объединением всех его образующих.

Объединение боковой поверхности конуса и его основания называется полной поверхностью конуса, а её площадь называется площадью полной поверхности конуса или, короче, площадью поверхности конуса и обозначается Sкон. Из этого определения следует, что

Sкон = Sбок + Sосн.

Если вокруг данной прямой — оси — вращать пересекающую её прямую, то при этом вращении образуется поверхность, которую называют круговой конической поверхностью или конической поверхностью вращения. Уравнение  + –  = 0 задаёт коническую поверхность вращения с осью вращения Oz (рис. 167). Из этого уравнения следует, что коническая поверхность является поверхностью второго порядка. (Подробнее о поверхностях второго порядка можно прочитать в «Дополнениях» — в конце этой книги.)

18.2. Сечения конуса

Определение. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением конуса.

Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники. На рисунке 168 осевым сечением конуса является треугольник ABP (АР = ВР). Угол АPВ называют углом при вершине осевого сечения конуса.

Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.

Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP).

Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).

Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением.

 Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками.

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги. 

 ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60°; б) в 90°. Найти площадь сечения.

Решение. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.

Хорда АВ окружности основания стягивает дугу в 60°, значит, △ AOB — правильный и АВ = R.

Рис. 172

Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S△ ABP = АВ•РC. Имеем: ОР = R (по условию); в △ AOB: ОС = ; в △ ОСР: CP =  = .

Тогда S△ ABP =  АВ•РС = .

Ответ: а) .

18.3. Касательная плоскость к конусу

Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.

Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.

Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.

18.4. Изображение конуса

Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).

Для достижения наглядности изображения невидимые линии изображают штрихами.

Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.

18.5. Развёртка и площадь поверхности конуса

Пусть l — длина образующей, R — радиус основания конуса с вершиной Р.

Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a), то получим развёртку поверхности конуса (рис. 176, б), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):

α = .

За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.

Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле

Sбок =  α•l2,(1)

где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = , получаем:

Sбок = πRl.(2)

Таким образом, доказана следующая теорема.

Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼

Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.

Sкон = πRl + πR2.(3)

Следствие. Пусть конус образован вращением прямоугольного треугольника ABC вокруг катета АС (рис. 177). Тогда Sбок = π•BC•АВ. Если D — середина отрезка АВ, то AB = 2AD, поэтому

Sбок = 2 π ВС•AD.(4)

Проведём DE ⟂ АB (E ∈ l = AС). Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А) имеем

 = ⇒ BC•AD = DE•АС.(5)

Тогда соотношение (4) принимает вид

Sбок = (2π•DE)•AC,(6)

т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.

Это следствие будет использовано в п. 19.7.

18.6. Свойства параллельных сечений конуса

Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Доказательство. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α, параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).

Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β, α || β, то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O1 = α ∩ РО.  Обозначим этот круг F1.

Рассмотрим гомотетию с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).

Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия отображает основание F конуса на его параллельное сечение — круг F1, при этом центр О основания отображается на центр О1 круга F1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии точка X отображается на точку X1 = РX ∩ α. Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:

 =  = k,(*)

где k — коэффициент гомотетии , т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.

А поскольку гомотетия является подобием, то круг F1, являющийся параллельным сечением конуса, подобен его основанию.

Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO1 : РО, где РO1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то

Sсечен : Sоснов = k2 = : PO2.

Теорема доказана. ▼

18.7.Вписанные в конус и описанные около конуса пирамиды

Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.

Для построения изображения правильной пирамиды, вписанной в конус:

—строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;

—соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;

—выделяют видимые и невидимые (штрихами) линии изображаемых фигур.

На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:

—прямоугольный треугольник (см. рис. 179);

—правильный треугольник (см. рис. 180);

—квадрат (см. рис. 181);

—правильный шестиугольник (см. рис. 182).

Определение. Пирамида называется описанной около конуса, если у них вершина общая, а основание пирамиды описано около основания конуса. В этом случае конус называют вписанным в пирамиду (рис. 183).

 ЗАДАЧА (3.080). В равносторонний конус вписана правильная пирамида. Найти отношение площадей боковых поверхностей пирамиды и конуса, если пирамида: а) треугольная; б) четырёхугольная; в) шестиугольная.

Решение. Рассмотрим случай а). Пусть R — радиус основания равностороннего конуса, РАВС — правильная пирамида, вписанная в этот конус (рис. 184); △ DPE — осевое сечение конуса, CF — медиана △ АBС. Тогда в △ АВС (правильный): АВ = R, OF = R; в △ DPE (правильный): ОР =  = R; в △ ОРF (∠ FOP = 90°):

PF =  = .

Так как CF — медиана △ АВС, то PF — высота равнобедренного треугольника АВР. Поэтому

S△ ABP =  AB•PF =  R•  = .

Обозначим: S1 — площадь боковой поверхности пирамиды, S2 — площадь боковой поверхности конуса. Тогда

S1 = 3S△ ABP = ,

S

2 = πR•PA = πR•2R = 2πR2.

Следовательно,

S1 : S2 = : 2πR2 = .

Ответ: а) .

 Во многих пособиях по геометрии за площадь боковой поверхности конуса принимают предел последовательности боковых поверхностей правильных вписанных в конус (или описанных около конуса) п-угольных пирамид при n → +∞. Действительно, Sбок. пов. пирам = •a•Poсн. пирам, где Рoсн. пирам — периметр основания пирамиды, а — апофема боковой грани. Для правильных описанных около конуса пирамид апофема a — постоянная величина, равная образующей l конуса, а предел последовательности периметров правильных многоугольников, описанных около окружности радиуса R основания конуса, равен 2πR — длине этой окружности. Таким образом, мы вновь получаем: Sбок = πRl. 

18.8. Усечённый конус

Пусть дан конус с вершиной Р. Проведём плоскость α, параллельную плоскости основания конуса и пересекающую этот конус (рис. 185). Эта плоскость пересекает данный конус по кругу и разбивает его на два тела: одно из них является конусом, а другое (расположенное между плоскостью основания данного конуса и секущей плоскостью) называют усечённым конусом. Таким образом, усечённый конус представляет собой часть полного конуса, заключённую между его основанием и параллельной ему плоскостью. Основание данного конуса и круг, полученный в сечении этого конуса плоскостью α, называются соответственно нижним и верхним основаниями усечённого конуса. Высотой усечённого конуса называется перпендикуляр, проведённый из какой-либо точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённого конуса. (Часто за высоту усечённого конуса принимают отрезок, соединяющий центры его оснований.)

Часть боковой поверхности данного конуса, ограничивающая усечённый конус, называется боковой поверхностью усечённого конуса, а отрезки образующих конуса, заключённые между основаниями усечённого конуса, называются образующими усечённого конуса. Так как все образующие данного конуса равны и равны все образующие отсечённого конуса, то равны все образующие усечённого конуса.

Построение изображения усечённого конуса следует начинать с изображения того конуса, из которого получился усечённый конус (рис. 186).

На рисунке 187 показана развёртка усечённого конуса.

Из теоремы 28 следует, что основания усечённого конуса — подобные круги.

Определения усечённой пирамиды, вписанной в усечённый конус и описанной около него, аналогичны определениям пирамиды, вписанной в конус и описанной около него.

Заметим, что построение изображений усечённой пирамиды, вписанной в усечённый конус и описанной около него, следует начинать с изображений того конуса или той пирамиды, из которых получены соответственно усечённые конус и пирамида.

Полной поверхностью усечённого конуса называется объединение боковой поверхности этого конуса и двух его оснований. Иногда полную поверхность усечённого конуса называют его поверхностью, а её площадь — площадью поверхности усечённого конуса. Эта площадь равна сумме площадей боковой поверхности и оснований усечённого конуса.

Усечённый конус может быть образован также вращением прямоугольной трапеции вокруг боковой стороны трапеции, перпендикулярной её основанию.

На рисунке 188 изображён усечённый конус, образованный вращением прямоугольной трапеции ABCD вокруг стороны CD. При этом боковая поверхность усечённого конуса образована вращением боковой стороны АВ, а основания его — вращением оснований AD и ВС трапеции.

18.9. Поверхность усечённого конуса

Выразим площадь Sбок боковой поверхности усечённого конуса через длину l его образующей и радиусы R и r оснований (R > r).

Пусть точка Р — вершина конуса, из которого получен усечённый конус; точки О, O1 — центры оснований усечённого конуса; AA1 = l — одна из образующих усечённого конуса (рис. 189).

Используя формулу (2) п. 18.5, получаем

Учитывая, что A1A = l, имеем

Sбок = πRl + π(R – r)PA1.(7)

Выразим PA1 через l, R и r. Так как O1A1 || OA и OO1 — высота усечённого конуса, то прямоугольные треугольники POA и PO1A1 подобны. Поэтому АО : А1O1 = PA : PA1 или

Подставив это значение РА1 в (7), получаем

Sбок = π(R + r)l.(8)

Таким образом, доказана следующая теорема.

Теорема 29. Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую. ▼

Площадь полной поверхности усечённого конуса находится по формуле:

Sполн = π•(R + r)•l + π•R2 + π•r2.

Следствие. Пусть усечённый конус образован вращением прямоугольной трапеции ABCD вокруг её высоты AD (рис. 190). Тогда Sбок = π (АВ + DC)•ВС. Если KЕ — средняя линия трапеции, то АВ + DC = 2KE, поэтому

Sбок = 2π•KE•BC.(9)

Проведём EF ⟂ ВС.  Из подобия прямоугольных треугольников ВСН и EFK имеем

BC : EF = BH : KE ⇒ ⇒ KE•BC = EF•BH.(10)

Тогда равенство (9) принимает вид

Sбок = (2π•EF)•ВH,(11)

т. е. боковая поверхность усечённого конуса равна произведению его высоты на длину окружности, радиус которой равен серединному перпендикуляру, проведённому из точки оси конуса к его образующей.

18.10. Объёмы конуса и усечённого конуса

Найдём объём конуса, высота которого равна h и радиус основания — R. Для этого расположим этот конус и правильную четырёхугольную пирамиду, высота которой равна h и сторона основания — R, так, чтобы их основания находились на одной и той же плоскости α, а вершины — также в одной и той же плоскости β, параллельной плоскости α и удалённой от неё на расстояние h (рис. 191).

Каждая плоскость, параллельная данным плоскостям и пересекающая конус, пересекает также пирамиду; причём площади сечений, образованных при пересечении обоих тел, относятся к площадям оснований этих тел, как квадраты их расстояний от вершин. А так как секущие плоскости для пирамиды и для конуса равноудалены от их вершин, то  = . Тогда  =  =  = π, значит, для объёмов этих тел выполняется:

Vкон : Vпир = π : 1 или Vкон :  R2•h = π : 1, откуда

Vкон =  πR2 •h.

Самостоятельно рассмотрите усечённые конус и пирамиду, расположенные в соответствии с условиями принципа Кавальери. Тогда вы получите формулу вычисления объёма усечённого конуса:

Vус. кон =  π•h•(R2 + r•R + r2).

Эту же формулу вы можете вывести, если используете идею подобия так же, как это сделано в случае с выводом формулы площади боковой поверхности усечённого конуса.

Используя принцип Кавальери, докажите, что объём каждого из тел, на которые конус разбивается его сечением плоскостью, проходящей через вершину (рис. 192), может быть вычислен по формуле V =  •h•Scегм, где h — длина высоты конуса, а Sceгм — площадь соответствующего сегмента основания конуса.