В гладком вертикальном цилиндре под подвижным поршнем массой M и площадью S находится идеальный одноатомный газ. Поршень в равновесии располагается на высоте h над дном цилиндра. После сообщения газу количества теплоты Q поршень приподнялся, а газ нагрелся. Найдите, на какой высоте H над дном цилиндра находится поршень. Давление в окружающей цилиндр среде равно p0.
Спрятать решение
Решение.
Как следует из условия, объём газа равен а давление равно
в течение всего процесса подвода теплоты. Согласно уравнению Клапейрона — Менделеева
где
— количество газа (в молях). Отсюда
После сообщения газу количества теплоты Q температура газа увеличилась на
а его объём возрос на
причём согласно первому началу термодинамики
где изменение внутренней энергии для одноатомного идеального газа
а работа газа в изобарическом процессе
Поскольку в изобарическом процессе получаем:
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом; II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ |
3 |
| Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. И (ИЛИ) В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.). И (ИЛИ) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. И (ИЛИ) Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины) |
2 |
| Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи. ИЛИ В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи |
1 |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла | 0 |
| Максимальный балл | 3 |
Раздел кодификатора ФИПИ/Решу ЕГЭ:
2018-11-01 ![]()
В теплоизолированном цилиндре, герметично закрытом теплонепроводящим поршнем массы $m$ и площадью сечения $S$, находится некоторое количество гелия. Вне сосуда давление равно нулю, а поршень находится в равновесии на некоторой высоте $H$ над дном цилиндра. Сверху на поршень аккуратно без толчка кладут большой брусок массы $2m$.
Вопрос 1. На сколько процентов уменьшится высота поршня над дном цилиндра в новом положении равновесия?
Вопрос 2. На сколько процентов изменится температура гелия?
Трением поршня о стенки сосуда пренебречь.

Решение:
Давление гелия $P_{0} = frac{mg}{S} Па$. В новом положении равновесия $P = frac{3mg}{S} = 3P_{0}$.
По закону изменения энергии найдем работу газа над поршнем с бруском:
$A = Delta E = 0 – 3mg (H – h)$ (1)
Так как сосуд теплоизолирован, то газ не получал и не отдавал тепло. По 1-му началу термодинамики
$A = – Delta U = – frac{3}{2} nu R (T – T_{0} )$
Из уравнений Менделеева-Клапейрона $P_{0}SH = nu RT_{0}, 3P_{0}Sh = nu RT$ следует, что
$frac{T}{T_{0} } = frac{3h}{H} Rightarrow T = T_{0} frac{3h}{H}$ и $A = – frac{3}{2} nu RT_{0} left ( frac{3h}{H} – 1 right ) = – frac{3}{2} P_{0}SH left ( frac{3h}{H} – 1 right ) = – frac{3}{2} mg (3h – H)$ (2)
Приравняем (1) и (2): $3mg (H – h) = 3mg (1,5h – 0,5H)$, найдем новую высоту $h = frac{1,5H}{2,5} = 0,6 H$, которая уменьшилась на 40%. $frac{T}{T_{0} } = frac{3h}{H} = 1,8$. Температура увеличилась на 80%.
На большой поршень площадью 1000 см2
гидравлического пресса, заполненного водой, встает человек массой 70 кг. На
какую высоту поднимется малый поршень (массой поршней можно пренебречь)
площадью 10 см2 ?
Решение.
Гидравлический пресс представляет
собой сообщающиеся сосуда (цилиндры) разного диаметра.
Вначале поршни были на
одном уровне, так как давления, создаваемые этими поршнями, были одинаковы.
Когда на большой поршень встанет человек, он создаст на воду дополнительное
давление p2 = mg/S2 , которое в соответствии с законом
Паскаля передается по всем направлениям одинаково. В результате из большего
цилиндра часть воды будет переходить в малый до тех пор, пока гидростатическое
давление столба высотой h1 не станет равным давлению p2 .
Таким образом,
ρgh1 = mg/S2
=> h1 = mg/S2ρg = m/ρS2 ;
h1
= 0,7 м.
Ответ: h1 = 0,7 м.
Источник: Пособие-репетитор для подготовки к централизованному тестированию. С.Н.Капельян, Л.А.Аксенович.
30. Молекулярная физика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В вертикальном цилиндре, закрытом лёгким поршнем, находится бензол ((C_6H_6)) при температуре кипения (t =80^circ C). При сообщении бензолу некоторого количества теплоты часть его превращается в пар, который при изобарном расширении совершает работу, поднимая поршень. Удельная теплота парообразования бензола ( L = 396cdot 10^3 )Дж/кг, а его молярная масса (M =78cdot 10^{-3}) – кг/моль. Какая часть подводимого к бензолу количества теплоты идёт на увеличение внутренней энергии системы? Объёмом жидкого бензола и трением между поршнем и цилиндром пренебречь. “Досрочная волна 2020 вариант 1”
По первому закону термодинамики [Q=Delta U+A,quad (1)] (Q) – количество теплоты, полученное системой, (Delta U) – изменение внутренней энергии, (A) – работа газа.
А количество теплоты, полученное системой равно [Q=Lm,quad (2)] где (m) – масса образовавшегося пара.
Так как процесс испарения прошел не до конца, то данный процесс изотермический, а значит работа газа будет совершаться за счет изменения массы пара [A=dfrac{m}{M}RT,quad (3)] где (T) – температура газа в Кельвинах.
Объединим (1), (2) и (3) и найдем отношение (dfrac{Delta U}{Q}) [dfrac{Delta U}{Q}=dfrac{Q-A}{Q}=1-dfrac{dfrac{m}{M}RT}{Lm}=dfrac{RT}{LM}=dfrac{8,31 text{ Дж/(К$cdot$моль)}cdot (273+80)text{ К}}{396cdot 10^3text{ Дж/кг}cdot 78cdot 10^{-3}text{ кг/моль}}approx 90,5 %]
Ответ: 90,5
Цикл тепловой машины, рабочим веществом которой является (nu) молей идеального одноатомного газа, состоит из изотермического расширения, изохорного охлаждения и адиабатического сжатия. Работа, совершённая газом в изотермическом процессе, равна (A), а КПД тепловой машины равен (eta). Максимальная температура в этом цикле равна (T_o). Определите минимальную температуру (T) в этом циклическом процессе.
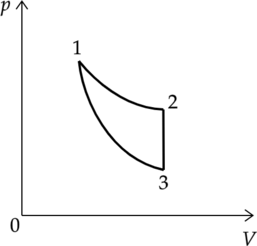
Процессы:
1-2 — изотермический
2-3 — изохорный
3-1 — адиабатический
КПД тепловой машины равен: [; ; ; ; eta = dfrac{A_text{ц}}{Q_text{н}} ; ; ; ; (1)] где (A_text{ц}) — работа, совершенная газом за цикл, (Q_text{н}) — количество теплоты, полученное газом от нагревателя.
Работа газа за цикл есть сумма работ газа в каждом процессе: [A_text{ц} = A_{1-2} + A_{2-3} + A_{3-1}] Так как в процессе 2-3 объем газа постоянен, то его работа равна нулю.
Тогда работа газа за цикл равна: [; ; ; ; A_text{ц} = A_{1-2} + A_{3-1} ; ; ; ; (2)] Далее необходимо найти количество теплоты (Q_text{н}), полученное газом от нагревателя.
Для этого запишем первое начало термодинамики для каждого процесса.
Процесс 1-2: [Q_{1-2} = A_{1-2} + Delta U_{1-2}] Так как процесс 1-2 изотермический, то изменение внутренней энергии газа (Delta U_{1-2}) равно нулю.
Объем газа увеличивается, следовательно, газ совершает положительную работу.
Отсюда получаем, что: [Q_{1-2} = A_{1-2} > 0 ; ; ; Rightarrow ; ; ; ; Q_{1-2} > 0] Процесс 2-3: [Q_{2-3} = A_{2-3} + Delta U_{2-3}] Так как процесс 2-3 изохорный, то работа газа (A_{2-3}) равна нулю.
Давление газа уменьшается, следовательно, его температура также уменьшается (для изохорного процесса (p sim T)).
Следовательно, изменение внутренней энергии газа отрицательно.
Отсюда получаем, что: [Q_{2-3} = Delta U_{2-3} < 0 ; ; ; Rightarrow ; ; ; ; Q_{2-3} < 0] Процесс 3-1:
Так как процесс 3-1 адиабатный, то (Q_{3-1} = 0): [; ; ; ; Q_{3-1} = A_{3-1} + Delta U_{3-1} ; ; ; Rightarrow ; ; ; ; A_{3-1} = – Delta U_{3-1} ; ; ; ; (3)] Таким образом, количество теплоты, полученное газом от нагревателя равно: [Q_text{н} = Q_{1-2}] [; ; ; ; Q_text{н} = A_{1-2} ; ; ; ; (4)] Подставим (2), (4) в (1): [eta = dfrac{A_{1-2} + A_{3-1}}{A_{1-2}}] [; ; ; ; eta = 1 + dfrac{A_{3-1}}{A_{1-2}} ; ; ; ; (5)] Подставим (3) в (5): [; ; ; ; eta = 1 – dfrac{Delta U_{3-1}}{A_{1-2}} ; ; ; ; (6)] Изменение внутренней энергии газа в процессе 3-1 равно: [; ; ; ; Delta U_{2-3} = dfrac{3}{2}nu R(T_1 – T_3) ; ; ; ; (7)] где (R) — универсальная газовая постоянная.
Подставим (7) в (6) и выразим искомую температуру: [eta = 1 – dfrac{dfrac{3}{2}nu R(T_1 – T_3)}{A_{1-2}}] [T_3 = T_1 – dfrac{2}{3nu R} (1 – eta)A_{1-2}] Температура (T_1) является максимальной в этом цикле, так как точка 1 на графике принадлежит изотерме 1-2, которая лежит выше, чем изотерма, проведенная через точку 3: (T_1 = T_o).
Следовательно, температура (T_3) является минимальной: (T_3 = T).
Работа (A_{1-2}) совершена газом в изотермическом процессе: (A_{1-2} = A).
Таким образом, искомая температура равна: [T = T_o – dfrac{2}{3nu R} (1 – eta)A]
Ответ: $T=T_o-dfrac{2}{3nu R}(1-eta)A$
В гладком вертикальном цилиндре под подвижным поршнем массой (M) и площадью (S) находится идеальный одноатомный газ. Поршень в равновесии располагается на высоте (h) над дном цилиндра. После сообщения газу количества теплоты (Q) поршень приподнялся, а газ нагрелся. Найдите, на какой высоте (H) над дном цилиндра находится поршень. Давление в окружающей цилиндр среде равно (p_o).
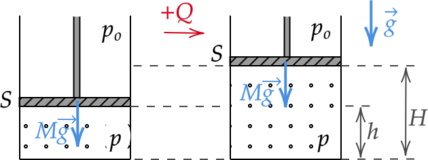
Рассматриваемый процесс — изобарный (так как поршень подвижный и количество вещества газа не изменяется).
Запишем первое начало термодинамики для изобарного процесса: [; ; ; ; Q = A+Delta U ; ; ; ; (1)] где (A) — работа газа, (Delta U) — изменение внутренней энергии газа.
Работа газа и изменение его внутренней энергии равны: [; ; ; ; A = pDelta V ; ; ; ; (2) ; ; ; ; ; ; ; ; ; ; ; Delta U = dfrac{i}{2}nu RDelta T ; ; ; ; (3)] где (p) — давление газа под поршнем, (Delta V) — изменение объема газа, (i) — число степеней свободы (для одноатомного газа (i = 3)), (nu) — количество вещества газа, (R) — универсальная газовая постоянная, (Delta T) — изменение температуры газа.
Подставим (2), (3) в (1): [Q = pDelta V + dfrac{3}{2}nu RDelta T] Для изобарного процесса справедливо равенство: (pDelta V = nu RDelta T).
Тогда уравнение (4) примет вид: [; ; ; ; Q = pDelta V + dfrac{3}{2}pDelta V = dfrac{5}{2}pDelta V ; ; ; ; (5)] Давление внутри сосуда складывается из атмосферного давления и давления, оказываемого поршнем (так как у него есть масса): [; ; ; ; p = p_o + dfrac{Mg}{S} ; ; ; ; (6)] где (g) — ускорение свободного падения.
Изменение объема, занимаемого газом, после сообщения теплоты равно: [; ; ; ; Delta V = (H-h)S ; ; ; ; (7)] Подставим (6), (7) в (5) и выразим высоту, на которой будет находиться поршень над дном цилиндра: [Q = dfrac{5}{2}left( p_o + dfrac{Mg}{S} right) (H-h)S] [H=h+dfrac{2Q}{5(p_oS+Mg)}]
Ответ: $H=h+dfrac{2Q}{5(p_oS+Mg)}$
Два одинаковых теплоизолированных сосуда соединены короткой трубкой с краном. В первом сосуде находится (nu_1) =3 моль гелия при температуре (T_1 = 350) К, во втором (nu_2) = 2 моль аргона при температуре (T_2 = 400) К. Кран открывают. В установившемся равновесном состоянии давление в сосудах становится (p = 6 ) кПа. Определите объём (V ) одного сосуда. Объёмом трубки пренебречь. Ответ дайте в м(^3) и округлите до тысячных.
Так как сосуды теплоизолированные, а газ не совершает работы, то изменение внутренней энергии равно 0, то есть [U_1+U_2=U] где (U_1) – внутренняя энергия первого сосуда, (U_2) – внутренняя энергия второго сосуда, (U) – внутренняя энергия сосудов после открытия краника.
Или [dfrac{3}{2}nu_1R T_1+dfrac{3}{2}nu_2RT_2=dfrac{3}{2}left(nu_1+nu_2right)RT] Отсюда установившаяся температура [T=dfrac{nu_1T_1+nu_2T_2}{nu_1+nu_2}] По закону Клапейрона – Менделеева [p2V=left(nu_1+nu_2right)RT] Отсюда объем одного сосуда [V=dfrac{left( nu_1T_1+nu_2T_2right)R}{2p}=dfrac{left( 3text{ моль} cdot 350text{ К}+2text{ моль} cdot 400text{ К}right)cdot 8,31 text{ Дж/(моль$cdot$ К)}}{2cdot 6cdot 10^3 text{ Па}}approx 1,28text{ м$^3$ }]
Ответ: 1,28
1 моль идеального одноатомного газа сначала изотермически расширили. Затем изохорно нагрели, при этом его давление возросло в 3 раза (см. рисунок). Какое количество теплоты получил газ на участке 2–3, если (T_1=100) К? Ответ дайте в Дж.
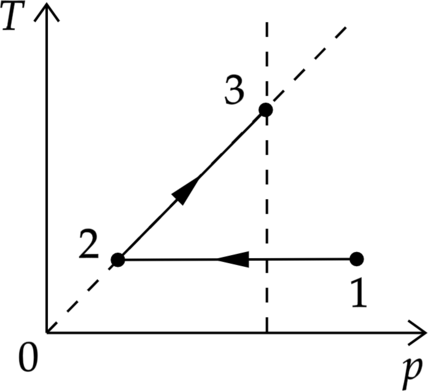
1. Воспользуемся первым законом термодинамики [Q=Delta U+A,] где (Q) – количество теплоты, полученное системой, (Delta U) – изменение внутренней энергии системы, (A) – работа газа.
Так как процесс изохорный, то работа газа равна 0. Распишем изменение внутренней энергии и получим [Q=dfrac{3}{2}nu R Delta T=dfrac{3}{2}nu R left(T_3-T_2right)] 2. Воспользуемся законом Шарля [dfrac{p_2}{T_2}=dfrac{p_3}{T_3} Rightarrow T_3=dfrac{p_3 T_2}{p_2}=3T_2] 3. По условию процесс 1–2 изотермический, значит [T_1=T_2] Следовательно, первый закон термодинамики выглядит [Q=dfrac{3}{2}nu R left(3T_1-T_1right)=3nu R T_1= 3cdot 1 text{ моль} cdot 8,31 text{ Дж/(моль $cdot$ К)}cdot 100text{ К}=2493text{ Дж}]
Ответ: 2493
Один моль одноатомного идеального газа совершает процесс 1–2–3, график которого показан на рисунке в координатах T–V, Известно, что в процессе 1–2 газ совершил работу 3 кДж, а в процессе 2–3 объём газа V увеличился в 2 раза. Какое количество теплоты было сообщено газу в процессе 1–2–3, если его температура Т в состоянии 3 равна 600 К? Ответ дайте в Дж.
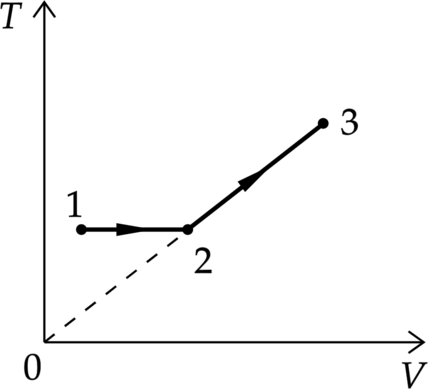
1.Проанализируем процессы
1–2 Процесс изотермический, по закон Бойля-Мариотта [p_1 V_1=p_2V_2] Значит возрастает объем и давление.
2–3 Температура увеличивается линейно объему, следовательно, процесс изобарный.
2. Количество теплоты, полученное в процессе 1–2–3, равно сумме количеств теплоты, полученных в процессах 1–2 и 2–3. [Q_{123}=Q_{12}+Q_{23}] 3. По первому закону термодинамики [Q=Delta U +A,] где (Q) – количество теплоты, полученное системой, (Delta U) – изменение внутренней энергии системы, (A) – работа газа.
Значит в процессе 1–2 изменение внутренней энергии равно 0, а количество теплоты [Q_{12}=A_{12}=3 text{ кДж}] В процессе 2–3 по условию объем возрос в 2 раза, значит по закону Гей-Люссака [dfrac{V_2}{T_2}=dfrac{V_3}{T_3}Rightarrow T_2=dfrac{V_2 T_3}{V_3}= dfrac{600text{ К}}{2}=300text{ К}] По закону Клапейрона–Менделеева [pV=nu R T] Значит количество теплоты, полученное в процессе 2–3 равно [Q_{23}=dfrac{3}{2}nu R left(T_3-T_2right)+pleft( V_3-V_2right)=dfrac{3}{2}nu R left(T_3-T_2right)+nu R left(T_3-T_2right)=dfrac{5}{2}nu R left(T_3-T_2right)] [Q_{23}=dfrac{5}{2}cdot 1 text{ моль} cdot 8,31 text{ Дж/(моль $cdot$ К)}left( 600 text{ К}- 300text{ К}right)= 6232,5 text{ Дж}] А общее количество теплоты [Q=Q_{12}+Q_{23}=6232,5 text{ Дж}+ 3000text{ Дж}=9232,5 text{ Дж}]
Ответ: 9232,5
На рисунке показан циклический процесс постоянное количество одноатомного газа. Работу, которую совершают внешние силы при переходе газа из состояния 2 в состояние 3, равна 5 кДж. Какое количество теплоты газ отдаёт за цикл холодильнику? Ответ дайте в кДж 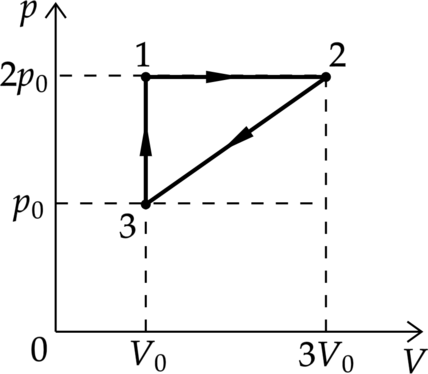
Работа внешних сил в процессе 2–3 равна площади под графиком. [A_{23}=dfrac{p_0+2p_0}{2}left(3V_0-V_0right)=3p_0V_0] (p) – давление, (V) – объем газа, (nu) – количество вещества, (T) – температура газа в Кельвинах.
Воспользуемся первым законом термодинамики [|Q_{text{ хол}}|=|Q_{23}|=Delta U_{23}+A_{32}=dfrac{3}{2}left( nu R T_2 -nu R T_3right)+ 3p_0V_0quad (1)] Также по уравнению Клапейрона – Менделеева [p_2V_2=nu R T_2= 2p_0 cdot 3V_0 =6p_0V_0 quad (2)] [p_2V_2=nu R T_3=p_0V_0 quad (3)] Подставим в (1) формулы (2) и (3) [|Q_{text{ хол}}|=dfrac{3}{2}left(6p_0V_0-p_0V_0right)+3p_0V_0= dfrac{21}{2}p_0V_0=dfrac{7}{2}A_{23}=3,5 cdot 5text{ кДж} =17,5text{ кДж}]
Ответ: 17,5

УСТАЛ? Просто отдохни
В теплоизолированном цилиндре, герметично закрытом теплонепроводящим поршнем массы m и площадью сечения S, находится некоторое количество водорода. Вне сосуда давление равно нулю, а поршень находится в равновесии на некоторой высоте H над дном цилиндра. Сверху, с такой же высоты H, над поршнем отпускают большой пластилиновый брусок массы 2m, который абсолютно неупруго соударяется с поршнем и прилипает к нему.
Вопрос 1. Во сколько раз уменьшилась высота поршня над дном цилиндра в новом положении равновесия?
Вопрос 2. На сколько процентов изменилась температура водорода? Трением поршня о стенки сосуда пренебречь.
Замечание: внутренняя энергия идеального двухатомного газа определяется по формуле
