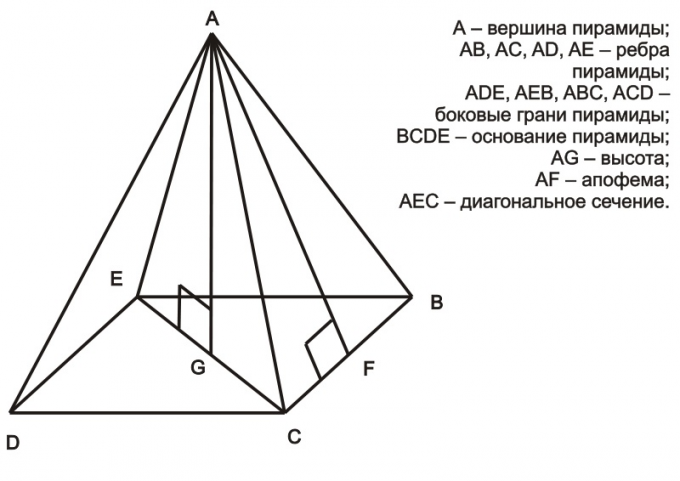
Одной из объемных фигур, изучаемых в курсе пространственной геометрии, является пирамида. Важной характеристикой этой фигуры является ее высота. В статье дадим определение высоты пирамиды и приведем формулы, через которые она связана с другими линейными характеристиками.
Что собой представляет пирамида
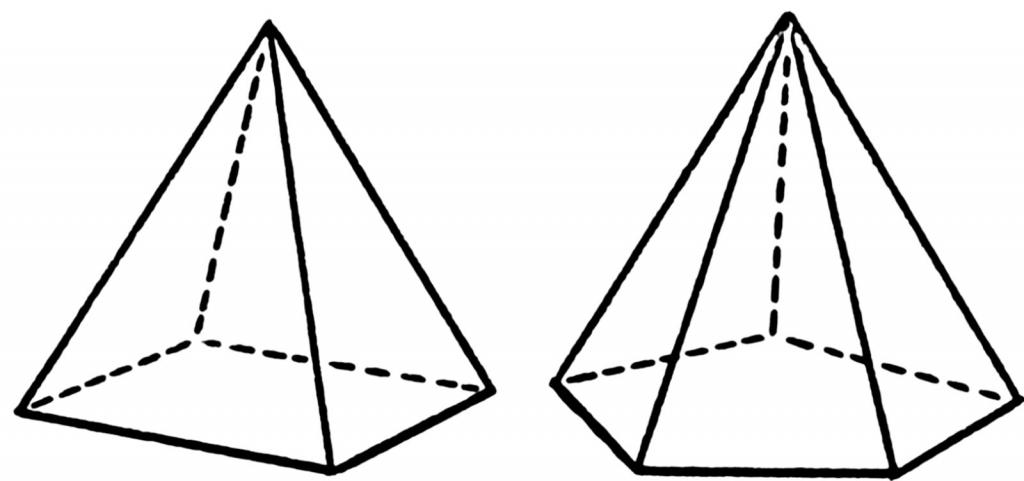
Под пирамидой понимают геометрическую фигуру пространственную, которая получается в результате соединения всех углов многоугольника с одной точкой пространства. Рисунок ниже демонстрирует расположение линий (ребер) для четырехугольной и пятиугольной пирамид.
Многоугольная грань фигуры называется ее основанием. Точка, где все треугольные грани соединяются, называется вершиной. Для определения высоты пирамиды отмеченные элементы являются важными.
Высота фигуры
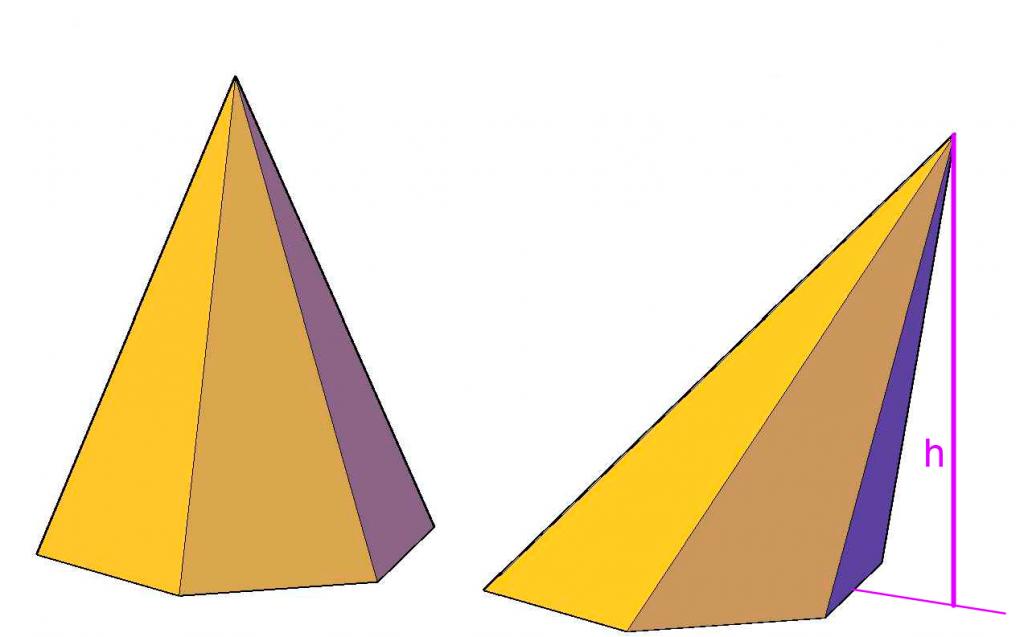
Высотой пирамиды называется перпендикуляр, который из ее вершины опущен на плоскость основания. Важно понимать, что из каждой вершины, принадлежащей основанию фигуры, тоже можно провести перпендикуляр к соответствующей треугольной грани, однако он высотой не будет являться. Высота пирамиды – это единственный перпендикуляр, который является одной из важных ее линейных характеристик.
Каждому школьнику известно, что любая плоская фигура обладает геометрическим центром (в физике ему соответствует центр масс). Например, геометрический центр для произвольного треугольника определяется точкой пересечения его медиан, для параллелограмма – точкой пересечения диагоналей. Если высота пирамиды пересекает ее основание в геометрическом центре, то фигура называется прямой. Пирамида прямая, имеющая в основании многоугольник с одинаковыми сторонами и углами, называется правильной.
Рисунок выше показывает, чем отличается неправильная пирамида от правильной. Видно, что высота неправильной фигуры лежит за пределами ее основания, в то время как у правильной шестиугольной пирамиды высота находится внутри фигуры, пересекая ее основание в центре геометрическом.
Важными свойствами всех правильных пирамид являются следующие:
- все боковые грани представляют собой равнобедренные треугольники и равны друг другу;
- длины боковых ребер и апофем являются одинаковыми.
Формулы для высоты правильной пирамиды
Существует четыре основных линейных характеристики для любой пирамиды правильной:
- сторона основания;
- боковое ребро;
- апофема боковой грани;
- высота фигуры.
Все они связаны математически друг с другом. Обозначим длину стороны основания символом a, высоту – h, апофему – hb и ребро – b. Формулы, которые эти величины связывают, имеют индивидуальный вид для соответствующей n-угольной пирамиды. Например, для правильной пирамиды четырехугольной высоту можно определить по формулам:
h = √(ab2 – a2/4);
h = √(b2 – a2/2).
Эти формулы следуют из теоремы Пифагора при рассмотрении соответствующих прямоугольных треугольников внутри пирамиды.
Если рассматривается фигура с треугольным основанием, тогда справедливы следующие формулы для высоты правильной пирамиды:
h = √(ab2 – a2/12);
h = √(b2 – a2/3).
Решение задачи с шестиугольной пирамидой
Предположим, что нам дана пирамида правильная с шестиугольным основанием. Известно, что высота основания пирамиды равна 13 см. Зная, что длина ее бокового ребра равна 10 см, необходимо вычислить объем и высоту правильной шестиугольной пирамиды.
Рисунок ниже показывает, как выглядит правильный шестиугольник.
Расстояние между любыми его двумя параллельными сторонами называется высотой. Не сложно показать, что эта высота ha связана с длиной стороны фигуры следующей формулой:
ha = a*√3
Подставляя в выражение значение ha, находим, что сторона основания a равна 7,51 см.
Высоту h фигуры можно определить, если рассмотреть прямоугольный треугольник, находящийся внутри пирамиды и состоящий из двух катетов (высота пирамиды и половина диагонали шестиугольного основания) и гипотенузы (боковое ребро). Тогда значение h будет равно:
h = √(b2 – a2) = √(100 – 56,4) = 6,6 см.
Объем пирамиды определяется как третья часть от произведения высоты фигуры на площадь ее основания. Площадь правильного шестиугольника равна:
S6 = n/4*a2*ctg(pi/n) = 6/4*a2*ctg(pi/6) = 3*√3/2*a2 = 3*√3/2*56,4 ≈ 146,53 см2.
Использованная для вычисления S6 формула является универсальной для произвольного правильного n-угольника.
Для определения объема фигуры остается подставить в соответствующую формулу найденные параметры:
V = 1/3*h*S6 = 1/3*6,6*146,53 = 322,366 см3.
Мы получили значение высоты пирамиды и рассчитали ее объем. Таким образом, поставленная задача решена.
Достаточно знать длину бокового ребра пирамиды, количество сторон многоугольника, лежащего в основании пирамиды, а также длину стороны основания (сторону многоугольника).
В основании правильной пирамиды всегда лежит правильный многоугольник. Любой правильный многоугольник можно вписать в окружность.
Есть такая формула:
a — длина стороны n-угольника (для правильного многоугольника).
L – длина окружности, описывающей этот многоугольник.
n – это количество сторон этого многоугольника
Если выразить эту формулу наоборот, то можно по стороне многоугольника найти длину окружности.
L=a*π/sin(180/n)
Зная длину окружности, можно найти радиус этой окружности:
L=2πR
R=L/(2π)
Подставляя L из первой формулы, получаем:
R = L/(2π) = a*π/(2π*sin(180/n)) = a/(2sin(180/n))
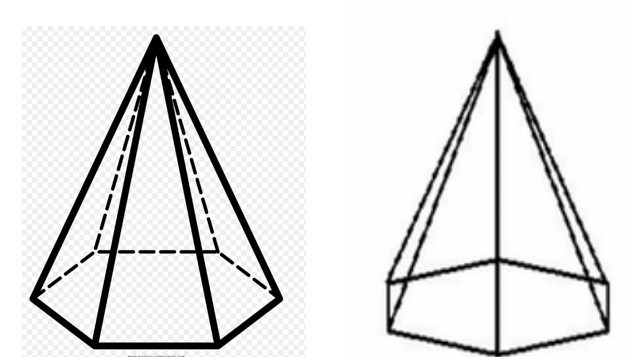
Теперь если приглядитесь к рисунку, то увидите, что радиус описанной окружности является также и катетом в прямоугольном треугольнике (игреком “y” на левой картинке).
А вертикальное ребро пирамиды это гипотенуза этого прямоугольного треугольника.
А искомая нам высота это второй катет этого прямоугольного треугольника.
По теореме Пифагора:
X²=Y²+h²
h²=X²-Y²
h=√(X²-Y²)
X нам известен – это длина боковой стороны пирамиды.
Y тоже известен – это расстояние от одного из углов основания пирамиды до центра пирамиды, и это же радиус описанной вокруг этого многоугольника окружности.
Y=R, а R равен: R=a/(2sin(180/n))
Итак подведём итог:
h=√(X²-Y²) = √(X²-R²) = √(X²-(a/(2sin(180/n)))²)
X – размер боковой стороны (ребра) пирамиды.
n – количество сторон многоугольника в основании.
a – размер стороны этого многоугольника в основании.
Более удобно эту формулу я отразил на рисунке.
Как найти высоту правильной пятиугольной пирамиды через сторону
Мастер
(1007),
на голосовании
7 лет назад
Голосование за лучший ответ
Alex
Просветленный
(27831)
7 лет назад
1. Вычисляем радиус описанной окружности – это катет.
2. Сторона пирамиды – гипотенуза, надо найти по теореме Пифагора второй катет. Всё, задача решена.
Леонид
Просветленный
(26204)
7 лет назад
НИКАК! Одни и те же стороны (величины) могут быть при разных высотах, от равенства сторон и высоты и нулевому углу между ними (в одном пределе), до нулевой высоты и угла между сторонами 360 градусов/5 (в другом пределе).
Как найти высоту в правильной пирамиде
Пирамида представляет собой многогранник, в основании которого лежит многоугольник, а грани его представляют собой треугольники, обладающие общей вершиной. Для правильной пирамиды справедливо то же определение, но в основании ее лежит правильный многоугольник. Под высотой пирамиды подразумевается отрезок, который проведен от вершины пирамиды к основанию, и этот отрезок перпендикулярен ему. Найти высоту в правильной пирамиде очень легко.
Вам понадобится
- В зависимости от ситуации, знать объем пирамиды, площадь боковых граней пирамиды, длину ребра, длину диаметра многоугольника в основании.
Инструкция
Одним из способов найти высоту пирамиды, и не только правильной – это выразить ее через объем пирамиды. Формула, с помощью которой можно узнать ее объем, выглядит так:
V = (S*h)/3, где S – площадь всех боковых граней пирамиды в сумме, h – высота данной пирамиды.
Тогда из этой формулы можно вывести другую, для нахождения высоты пирамиды:
h = (3*V)/S
К примеру, известно, что площадь боковых граней пирамиды 84 см², а объем пирамиды равен 336 куб.см. Тогда найти высоту можно так:
h = (3*336)/84 = 12 см
Ответ: высота данной пирамиды 12 см
Рассматривая правильную пирамиду, в основании которой лежит правильный многоугольник, можно прийти к выводу, что треугольник, образованный высотой, половиной диагонали и одной из граней пирамиды, представляет из себя прямоугольный треугольник (например, это треугольник АEG на рисунке выше). Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов (a² = b² + c²). В случае с правильной пирамидой, гипотенуза – это грань пирамиды, один из катетов – половина диагонали многоугольника в основании, а другой катет – высота пирамиды. В таком случае, зная длину грани и диагонали, можно вычислить и высоту. В качестве примера можно рассмотреть треугольник AEG:
AE² = EG²+GA²
Отсюда высоту пирамиды GA можно выразить так:
GA = √(AE²-EG²).
Чтобы было более понятно, как находить высоту правильной пирамиды, можно рассмотреть пример: в правильной пирамиде длина грани 12 см, длина диагонали многоугольника в основании – 8 см. Исходя из этих данных, требуется найти длину высоты этой пирамиды.Решение: 12² = 4² + c², где с – неизвестный катет (высота) данной пирамиды (прямоугольного треугольника).
144 = 16 + 128
Таким образом, высота данной пирамиды √128 или, приблизительно, 11.3 см
Источники:
- правильная четырехугольная пирамида найти высоту
- Решение заданий С2 ЕГЭ по математике
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Высота пирамиды опускается из вершины пирамиды в центр основания, вне зависимости от того какая фигура находится в основании. Если основанием пирамиды является правильный многоугольник, то вычислить высоту пирамиды становится возможным при наличии разных данных, так как центр основания будет центром вписанной или описанной вокруг многоугольника окружности. Найти высоту пирамиды через ребро, можно соединив центр многоугольника с любым углом в основании, таким образом, получив внутри пирамиды прямоугольный треугольник. Проведенный отрезок для фигуры в основании является радиусом описанном окружности R, и он вместе с высотой пирамиды являются катетами, а ребро b – гипотенузой. Из теоремы Пифагора, высота вычисляется следующим образом:
Если же в задаче дана апофема пирамиды l, то центр многоугольника в основании нужно соединить с центром ребра в основании, куда опускается апофема. Данный отрезок для многоугольника будет уже радиусом вписанной окружности r, а в остальном формула остается абсолютно аналогичной предыдущей: