Как найти высоту правильной треугольной усеченной пирамиды, если известно стороны основания и боковое ребро? Помогите!!!
@futurelawyer
Знаток
(498),
закрыт
5 лет назад
Кирилл Семёнов
Просветленный
(28409)
5 лет назад
1 Найти диагонали оснований по теореме Пифагора (основания я так понимаю квадраты)
2. От большего основаия отнять меньшее и поделить на 2. Так найдём отрезок от угла основания до того места, где опустится высота.
2 От квадрата ребра – квадрат отрезка и извлечь корень. Это и будет высота.
Дополним усеченную пирамиду до полной. Так как в правильной пирамиде высота проходит через центр окружно-
сти, вписанной в основание, то О и Ο1 — центры окружностей, вписанных в АВС и А1В1С1.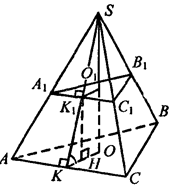
Проведем SK┴AC, а значит, и SK1┴A1C1. Тогда по теореме о трех пер-
пендикулярах ОК┴АС и ОК1┴А1С1. Значит, ОК и O1К1 — радиусы окружностей, вписанных в правильные треугольники АВС и А1B1C1
![]()
Далее, проведем Κ1Η┴ΚΟ. Тогда Κ1Ο1ΟΗ — прямоугольник, значит, К1Н=OO1
Так как ∟Κ1ΚΗ является линейным углом двугранного угла ме-
жду основанием и боковой гранью, то ∟Κ1ΚΗ =60° (по условию).
Тогда в ∆Κ1ΚΗ: Κ1Η=ΚΗ· tg∟K1KH = √3 KH.
Основания правильной усеченной пирамиды представляют собой правильные многоугольники, зная стороны которых можно найти все остальные параметры, такие как внутренний угол, периметр, площадь, радиусы вписанной и описанной окружностей.
γ=180°(n-2)/n
P=n(a+b+d)
S_a=(na^2)/(4 tan〖(180°)/n〗 )
S_b=(nb^2)/(4 tan〖(180°)/n〗 )
r_a=a/(2 tan〖(180°)/n〗 )
r_b=b/(2 tan〖(180°)/n〗 )
R_a=a/(2 sin〖(180°)/n〗 )
R_b=a/(2 sin〖(180°)/n〗 )
Зная высоту усеченной пирамиды, можно найти ее боковое ребро и апофему, рассмотрев прямоугольные трапеции, соединяющие их через радиусы вписанной и описанной окружностей в основаниях. Из прямоугольных трапеций построив дополнительный прямоугольный треугольник, легко вычислить боковое ребро или апофему как гипотенузу, а также найти углы при основаниях. (рис. 50.3, 50.4)
f=√(h^2+(b/2-a/2)^2 )=√(h^2+(b-a)^2/4)
cosβ=(r_b-r_a)/f
α=180°-β
d=√(h^2+(R_b-R_a )^2 )
cosδ=(R_b-R_a)/d
ε=180°-δ
Чтобы найти площадь боковой поверхности, нужно вычислить площадь каждой грани усеченной пирамиды, а затем умножить полученное значение на количество сторон в основаниях. Вычислить площадь полной поверхности усеченной пирамиды, зная стороны и высоту, нужно, преобразовав высоту в апофему по приведенным выше формулам, и сложив площадь боковой поверхности с площадями оснований.
S_(б.п.)=nf (a+b)/2
S_(п.п.)=S_(б.п.)+S_(осн.1,2)=n(f (a+b)/2+a^2/(4 tan〖(180°)/n〗 )+b^2/(4 tan〖(180°)/n〗 ))
Объем усеченной пирамиды, зная стороны и высоту, равен одной трети высоты умноженной на сумму площадей оснований с радикалом из их произведения.
V=1/3 h(S_осн1+S_осн2+√(S_осн1 S_осн2 ))
ВИДЕОУРОК
Усечённой пирамидой ABCDA1B1C1D1 называется часть пирамиды SABCD, заключённая между её основанием и секущей плоскостью, параллельной основанию.

Основаниями усечённой пирамиды называются параллельные грани ABCD и A1B1C1D1 (ABCD – нижнее основание, A1B1C1D1 – верхнее основание).
Высотой усечённой пирамиды называется отрезок прямой, перпендикулярный её основаниям и заключённый между их плоскостями.
Усечённая пирамида называется правильной, если её основания – правильные многоугольники и прямая, соединяющая центры оснований, перпендикулярна плоскости оснований.
Апофемою правильной усечённой пирамиды называют высоту её боковой грани.
Свойства усечённой пирамиды.
Основания – подобные многоугольники.
Боковые грани – трапеции.
Отношение высоты к высоте пирамиды, из которой она получена, равно отношению разности сторон одной грани к длине нижнего основания этой самой грани.
Поверхность усечённой пирамиды.
Площадь боковой поверхности усечённой пирамиды равна сумме площадей её боковых граней.
Полная поверхность усечённой пирамиды равна сумме площади боковой поверхности и площадей оснований.
Боковая поверхность правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.

где Р и Р1 – периметры оснований, m – апофема усечённой пирамиды.
Правильная четырёхугольная усечённая пирамида.

Правильная треугольная усечённая пирамида.

Правильная шестиугольная усечённая пирамида.

ЗАДАЧА:
В правильной четырёхугольной усечённой пирамиде стороны оснований равны 5 и 11 дм, а диагональ пирамиды – 12 дм. Определите боковую поверхность пирамиды.
РЕШЕНИЕ:
В усечённой пирамиде АС1 имеем
А1В1 = В1С1 = С1D1 = D1А1 = 5 дм,
АВ = ВС = СD = DА = 11 дм и
А1С = 12 дм.
Найти боковую поверхность.

Из вершины А1 проведём А1N ⊥ AB и А1M ⊥ AC, тогда А1N – апофема пирамиды.
Боковая поверхность
Sбок = 1/2 (P + P1) × A1N.
где P = 4AB = 44
дм, а
P1 = 4A1B1 = 20
дм.
В квадратах АВСD и А1В1С1D1 по иіх сторонам определяем диагонали
АС = 11√͞͞͞͞͞2 (дм),
A1С1 = 5√͞͞͞͞͞5 (дм).
Рассмотрев равнобедренную трапецию АА1С1С, находим

и соответственно

Тогда из прямоугольного ∆ А1MC находим высоту пирамиды

Из равнобедренного прямоугольного ∆ AMN (∠ ANM = 90°), гипотенуза которого AM = 3√͞͞͞͞͞2 (дм), находим сторону

Апофему данной пирамиды найдём из прямоугольного

Подставляя найденные значения P, P1 и A1N в формулу боковой поверхности пирамиды, получим:
Sбок = 1/2 (44 + 20)×5 = 160 (дм2).
ОТВЕТ:
S = 160 дм2 = 1,6 м2.
ЗАДАЧА:
Высота правильной четырёхугольной усечённой пирамиды
равна 4
см. Стороны оснований равны 2
см и
8 см. Найдите площадь диагональных сечений.
РЕШЕНИЕ:
Начертим чертёж.
Диагональные сечения
AA1C1D и BB1D1D– равные равнобедренные трапеции с высотой ОО1 = h = 4 см и с основаниями
– диагоналями оснований АС и А1С1 та ВD и В1D1 соответственно. ABCD – квадрат, а поэтому
AC2 = AD2 + CD2 =
= 82 + 82 = 128,
AC = √͞͞͞͞͞128 = 8√͞͞͞͞͞2 (cм).
A1B1C1D1 – квадрат, а поэтому
A1C12 = A1D12 + C1D12 = 22 + 22 = 8,
A1C1 = √͞͞͞͞͞8 = 2√͞͞͞͞͞2 (cм).

ОТВЕТ: 20√͞͞͞͞͞2 (cм2)
ЗАДАЧА:
В правильной четырёхугольной усечённой пирамиде высота
равна 2
см, а стороны оснований – 3 см и 5
см. Найдите диагональ этой пирамиды.
РЕШЕНИЕ:
Начертим чертёж.
Диагональным сечением данной пирамиды
является равнобедренная трапеция АА1С1С.
Так как
А1С1 и АС –
диагонали квадратов, А1В1С1D1 и ABCD, то
А1С1 = А1В1 ∙ √͞͞͞͞͞2 = 3√͞͞͞͞͞2 (см) и
АС = АВ ∙ √͞͞͞͞͞2 = 5√͞͞͞͞͞2 (см).
Проведём
А1К ⊥
АС
и С1Н ⊥ АС. Тогда А1С1НК – прямоугольник
и А1С1 =
КН. Так что, прямоугольные треугольники АА1К и СС1Н равны по гипотенузе и катету.
Тогда,
АК = СН = 1/2 (АС – А1С1) =
= 1/2 (5√͞͞͞͞͞2 – 3√͞͞͞͞͞2) = √͞͞͞͞͞2 (см).
Тогда,
СК = АС – АК = 5√͞͞͞͞͞2 – √͞͞͞͞͞2 =
4√͞͞͞͞͞2 (см),
и по
теореме Пифагора в ∆ А1СК:

ОТВЕТ: 6 см
ЗАДАЧА:
В правильной четырёхугольной пирамиде плоскость, проведённая
параллельно основанию, делит высоту пирамиды пополам. Найдите сторону основания,
если площадь сечения равна 36 см2.
РЕШЕНИЕ:
Пусть SABCD – данная правильная пирамида,
основание – квадрат
ABCD, SO – высота, O –
точка пресечения диагоналей квадрата, φ – плоскость сечения, О1 –
точка пересечения φ и SO, φ ∥ (ABC), S = 36 cм2.
Поскольку φ ∥ (ABC),
то прямые пересечения 𝜑 и боковых граней параллельны соответственно рёбрам
основания:
A1B1 ∥ AB, B1C1 ∥ BC, C1D1 ∥ CD,
A1D1 ∥ AD, 𝜑 ⊥ SO,
можно рассмотреть гомотетию с центром S и коэффициентом

которая преобразует квадрат ABCD в квадрат
А1В1С1D1, стороны которого в два раза меньше, а
SABCD = 4SА1В1С1D1 = 4 ∙ 36 (см2).
SABCD = a2 = 4 ∙
36,
a = 2 ∙ 6
= 12 (см).
ОТВЕТ: 12 см
Задания к уроку 10
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Прямые и плоскости в пространстве
- Урок 2. Прямая призма
- Урок 3. Наклонная призма
- Урок 4. Правильная призма
- Урок 5. Параллелепипед
- Урок 6. Прямругольный параллелепипед
- Урок 7. Куб
- Урок 8. Пирамида
- Урок 9. Правильная пирамида
- Урок 11. Цилиндр
- Урок 12. Вписанная и описанная призмы
- Урок 13. Конус
- Урок 14. Усечённый конус
- Урок 15. Вписанная и описанная пирамиды
- Урок 16. Сфера и шар
- Урок 17. Комбинация тел



