Основания правильной усеченной пирамиды представляют собой правильные многоугольники, зная стороны которых можно найти все остальные параметры, такие как внутренний угол, периметр, площадь, радиусы вписанной и описанной окружностей.
γ=180°(n-2)/n
P=n(a+b+d)
S_a=(na^2)/(4 tan〖(180°)/n〗 )
S_b=(nb^2)/(4 tan〖(180°)/n〗 )
r_a=a/(2 tan〖(180°)/n〗 )
r_b=b/(2 tan〖(180°)/n〗 )
R_a=a/(2 sin〖(180°)/n〗 )
R_b=a/(2 sin〖(180°)/n〗 )
Зная высоту усеченной пирамиды, можно найти ее боковое ребро и апофему, рассмотрев прямоугольные трапеции, соединяющие их через радиусы вписанной и описанной окружностей в основаниях. Из прямоугольных трапеций построив дополнительный прямоугольный треугольник, легко вычислить боковое ребро или апофему как гипотенузу, а также найти углы при основаниях. (рис. 50.3, 50.4)
f=√(h^2+(b/2-a/2)^2 )=√(h^2+(b-a)^2/4)
cosβ=(r_b-r_a)/f
α=180°-β
d=√(h^2+(R_b-R_a )^2 )
cosδ=(R_b-R_a)/d
ε=180°-δ
Чтобы найти площадь боковой поверхности, нужно вычислить площадь каждой грани усеченной пирамиды, а затем умножить полученное значение на количество сторон в основаниях. Вычислить площадь полной поверхности усеченной пирамиды, зная стороны и высоту, нужно, преобразовав высоту в апофему по приведенным выше формулам, и сложив площадь боковой поверхности с площадями оснований.
S_(б.п.)=nf (a+b)/2
S_(п.п.)=S_(б.п.)+S_(осн.1,2)=n(f (a+b)/2+a^2/(4 tan〖(180°)/n〗 )+b^2/(4 tan〖(180°)/n〗 ))
Объем усеченной пирамиды, зная стороны и высоту, равен одной трети высоты умноженной на сумму площадей оснований с радикалом из их произведения.
V=1/3 h(S_осн1+S_осн2+√(S_осн1 S_осн2 ))
Помогите найти высоту правильной усеченной четырёхугольной пирамиды если известны стороны ее оснований и боковое ребро.
Знаток
(483),
закрыт
10 лет назад
Сергей Чечеренко
Мастер
(2303)
14 лет назад
Пусть a – сторона меньшего основания, b – сторона большего основания, с – боковое ребро. Тогда высота будет равна:
h = квадратный корень (с^2-0,5*(b-a)^2), где ^2 – возведение в квадрат
Александр Гармаш
Мастер
(2321)
14 лет назад
1 Найти диагонали оснований по теореме Пифагора (основания я так понимаю квадраты)
2. От большего основаия отнять меньшее и поделить на 2. Так найдём отрезок от угла основания до того места, где опустится высота.
2 От квадрата ребра – квадрат отрезка и извлечь корень. Это и будет высота.
Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту
Формулы усеченной пирамиды
Для расчёта всех основных параметров усеченной пирамиды воспользуйтесь калькулятором.
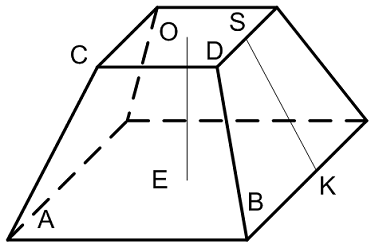
Площадь верхнего основания правильной усеченной пирамиды
$$
S_{верх.основ} = {N * CD^2 over 4 * tan(180/N)}
$$
Площадь нижнего основания правильной усеченной пирамиды
$$
S_{нижн.основ} = {N * AB^2 over 4 * tan(180/N)}
$$
Объём усеченной пирамиды
$$
V = {1 over 3} * OE * (S_{верх.основ} + sqrt{S_{верх.основ} * S_{нижн.основ}} + S_{нижн.основ})
$$
Апофема усеченной пирамиды
Так как боковая сторона усеченной пирамиды – это трапеция, то высота этой трапеции и будет апофемой усеченной пирамиды
$$
SK = sqrt{AC^2 – ({(AB – CD)^2 + AC^2 – BD^2 over 2 * (AB – CD)})^2}
$$
Площадь боковой поверхности
Площадью боковой поверхности усеченной пирамиды является сумма всех боковых сторон, каждая боковая сторона является трапецией
$$
S_{Бок.стороны} = {1 over 2} * SK * (CD + AB)
$$

Усечённая пирами́да — многогранник, часть пирамиды, заключенная между основанием и плоскостью, параллельной основанию.
Связанные определения[править | править код]
- Основание изначальной пирамиды, а также параллельная ему грань называются основаниями усечённой пирамиды.
- Остальные грани называются боковыми.

Правильная усечённая пирамида
- Если изначальная пирамида правильная то её усечённая пирамида также называется правильной.
- Высота боковой грани называется апофемой.
Свойства[править | править код]
- Боковые грани усечённой пирамиды представляют собой трапеции.