Как найти высоту предмета на местности - Сайт, где вы сможете решить свои вопросы

Иллюстрация – Как узнать высоту?

Приветствую Вас, уважаемый читатель!

Как-то в юности я занимался альпинизмом и ориентированием на местности, и не знаю как сейчас, но в то время нужно было обязательно знать раздел “Выживание в экстремальных условиях”, чтобы сдать экзамен и получить какой-либо разряд!

Собственно, решил поделиться с Вами и написать вкратце данную статью, полагая, что это будет очень познавательно и интересно! На самом деле способов еще гораздо больше, чем описано здесь, но они практически схожи, и вы в процессе чтения, вникнув в суть – сможете сами моделировать ситуации, и понять, что всё не так уж и сложно.

Ну что же, поехали…

Конечно не часто, но бывают в нашей жизни ситуации и обстоятельства, когда нужно знать высоту или расстояние до какого-либо объекта, например дома, дерева, да или похвастаться перед подругой))). Возможно придется строить траекторию для установки спутниковой тарелки, чтобы сигнал “стрелял” обходя высотки и не мешали кроны деревьев… ))) А мало ли, что еще…

Как ни парадоксально, но не забираясь с рулеткой на объект – расчет сделать не сложно, при том, что каждый метод может дать довольно точный результат. Конечно, с точностью до миллиметров не вычислить искомое значение, но погрешность будет точно уж небольшой.

Высота по отбрасываемой тени

Если погода солнечная и четко прослеживается тень, выбираем на объекте нижнюю контрольную точку от которой берет начало отбрасываемая тень будь-то дома, дерева, столба и пр.

Далее, ищем конец тени и производим замер длины тени.
После чего фиксируем в вертикальном положении любой предмет (на фото ниже – это обычный колышек) и аналогично замеряем длину его тени, а потом еще и высоту от точки начала тени до верхушки предмета.

Надеюсь, что у вас нет сомнения, что на фотографии треугольники с катетами Х1, Y1 и X2, Y2 подобны? Расчет строится на геометрическом свойстве подобных треугольников в которых отношения сторон равны и искомая высота объекта Y1 находится так:

Y1 (Высота столба) = (Y2*X1) / X2

Авторское фото – Вычисление высоты столба

Подручный предмет

Здесь требуется отойти от объекта и с помощью подручного предмета на вытянутой руке (ручки, карандаша, палки) замерить высоту. Конец предмета должен совпасть с верхней точкой объекта, а нижнюю точку требуется зафиксировать большим пальцем руки.

Иллюстрация – замер высоты

Разверните предмет горизонтально так, чтобы низ его по-прежнему оставался у основания объекта, а кончик касался земли и указывал на определенную точку. Важно запомнить эту точку или, если есть помощник, попросить встать на эту точку. Как раз эта точка будет являться точкой проекции верхушки на землю и теперь остается только замерить расстояние.

Угол падения и угол отражения

А если солнца нет и идет дождь, тоже не беда!

Согласно закону преломления из физики, о том что угол падения равен углу отражения – в зеркальном отражении любой лужи вы можете найти верхушку объекта и зная свой рост и расстояния соответственно, – получить искомую высоту (см.рисунок ниже).

Иллюстрация – Отражение

Зафиксируйте точку О любым предметом, брошенным в лужу. Таким образом вы сможете измерить расстояния ОА, ОА1.

Зная все необходимые величины и основываясь на свойствах подобных треугольников, получите высоту, которая будет равна:

АВ = (А1В1 * ОА) / ОА1

Барометр и немного юмора

Нам понадобится немного знаний физики. Из школьного курса известно, что атмосферное давление зависит от высоты над уровнем моря и измерив давление у основания объекта и на вершине – можно вычислить расстояние подъема.

Средняя величина уменьшения атмосферного давления составляет 1 мм. рт. столба на каждые 12 м. высоты или 133,32 Па (Паскаль), что – то же самое. Поэтому, независимо от того, в каких единицах получено значение давления – вы всегда сможете посчитать высоту.А если у вас есть секундомер (он есть в каждом телефоне), то сбросьте барометр с высоты, при этом засекая время его падения )))))).

Путь, пройденный телом в свободном падении равен:

S = (g*t^2)/2, где:

g – ускорение свободного падения – 9.8 м./с^2;

t – время по секундомеру, с.

Определяем высоту объекта на расстоянии от вас

Для определения высоты нам в любом случае требуется расстояние до объекта, но основание его нам не доступно, – по-этому измерение нельзя произвести непосредственно.

Чтобы вычислить расстояние, нам нужно:

Остановиться напротив объекта и зафиксировать эту точку (На рисунке точка А).
Повернуться под прямым углом (на 90 град.) и сделать несколько шагов. Эта точка будет являться точкой О (здесь нужно воткнуть длинный предмет, например палку).
Пройти то же расстояние, что и от А к О, и в том же направлении. Отметить каким-либо предметом (точка В).
Повернуться под прямым углом (на 90 град.) и удаляться от объекта (в сторону точки Y) до тех пор, пока установленный ваш предмет в точке О не будет совмещен с объектом.
Расстояние от вас (Y) до точки В – это и есть расстояние от точки А до объекта (Х).

Иллюстрация – вычисление расстояния до объекта

Теперь, зная расстояние до объекта, переходим к вычислению его высоты.

Иллюстрация – вычисление высоты объекта

Для простоты построения опять же подобных треугольников – берется шест с подвижной планкой (две доски сбиваются гвоздем). Устройство фиксируется в точке А, планка настраивается (при помощи врожденного глазомера в каждого из нас) на верхнюю точку объекта (Х1) – как показано на иллюстрации, после чего фиксируется.

Далее, отмечается на земле точка С.

В итоге мы получаем два треугольника СХХ1 и САА1, которые подобны между собой. Зная расстояние ХС, АС и АА1 находим искомую высоту Н объекта!

Высота Н = (АА1 * ХС) / АС.
____________________

Если Вам было интересно, ставьте палец вверх и подписывайтесь на канал!

Как определить высоту объекта вблизи или на расстоянии? Основные 5 способов!

1. Если диагонали равны, то это не значит, что у вас ровный дом. Почему? Рассказываю историю!

2. Почему основной типоразмер изделий металлопроката составляет в длину 11,7 м.?

3. Варианты построения прямых углов при строительстве дома и проверка углов при уже возведенном сооружении.

Источник

Определение высоты
некоторых предметов

Рекомендуем
несколько способов, при помощи которых можно определить высоту предметов.

1.
По тени. В
солнечный день можно определить высоту предмета по его тени, руководствуясь
следующим правилом: высота измеряемого предмета во столько раз больше высоты
известного вам предмета (палки, удочки), во сколько раз тень от
измеряемого предмета больше тени от палки, удоччки.

Если при
измерении окажется, что тень от палки или удочки в 2 раза больше длины палки
или удочки, то высота измеряемого предмета будет в 2 раза меньше длины его
тени, а если тень от палки или удочки будет равна их длине, высота измеряемого
предмета также равна высоте своей тени.

2.
При помощи равнобедренного треугольника. Приближаясь к
предмету (например, к дереву) или удаляясь от него, установить треугольник у
глаза так, чтобы один из его катетов был направлен отвесно, а другой совпал с линией
визирования на вершину дерева. Высота дерева будет равняться расстоянию до
дерева (в шагах) плюс высота до глаз наблюдателя.

3. По шесту. Взять шест, равный своему росту, и установить его на таком расстоянии
от предмета (дерева), чтобы лёжа можно было видеть верхушку дерева на одной
прямой с верхней точкой шеста.

Высота
дерева будет равна расстоянию от головы наблюдателя до основания дерева.

4. При помощи высотомера со стрелкой.
Изготовив прибор по данному чертежу, можно приступить к определению
высоты какого-либо предмета. Находясь на различном расстоянии от
предмета, надо следить, чтобы при визировании вершины дерева показания стрелки
не выходили за пределы шкалы.

При
визировании следует приложить глаз к отверстию сбоку прибора и, наклонив прибор,
добиться, чтобы вторая визирная точка (угол на другом конце прибора) совпала с
вершиной визируемого предмета. Стрелка укажет число, на которое следует
умножить расстояние до предмета, чтобы получить его высоту. К этому
прибавляется выста прибора во время визирования.

5.
При помощи лужи. Если недалеко от дерева находится
лужа, надо стать так, чтобы она помещалась между вами и предметом, а затем при
помощи горизонтально положенного зеркальца найти в воде отражение вершины
деерва. Высота дерева будет во столько раз больше роста человека, во сколько
раз расстояние от него до лужи больше, чем расстояние от лужи до наблюдателя.

Источник

В полевых условиях иногда бывает очень важно и полезно владеть простейшими прикладными способами измерений на местности. Например способами определения высоты дерева или любого другого предмета на местности.

Простые способы определения высоты дерева или любого другого предмета по тени, шесту, лужице или зеркалу, прямоугольному треугольнику.

Высоту дерева или любого другого предмета на местности очень просто можно определить по тени, шесту, лужице или зеркальцу, и прямоугольному треугольнику.

Способ определения высоты дерева или другого предмета по своему росту и длине тени.

Если на ровном месте измерить шагами длину своей тени, а затем длину тени, отбрасываемой деревом илипредметом, то искомую высоту легко вычислить из пропорции :

АК/ак = КЕ/ке

где АК — высота дерева (В), КЕ — тень дерева (D), ак — ваш рост (b), ке — ваша тень (d).

Например длина вашей тени d равна трем шагам, тень дерева D равна девяти шагам, то есть тень дерева длиннее вашей тени в три раза. Если принять ваш рост за 1,5 метра, то высота дерева будет В = 1,5 х 3 = 4,5 метра.

Способ определения высоты дерева или другого предмета по шесту и своему росту.

Этот же способ можно применить при пасмурной погоде, когда тени от предметов не видны. В этом случае для измерения нужно взятьшест, равный длине вашего роста. Шест этот надо установить на таком расстоянии от дерева, чтобы лежа можно было видеть верхушку дерева на одной прямой линии с верхней точкой шеста. Тогда высота дерева равна расстоянию от вашей головы до основания дерева, то есть АС = ВС.

Способ определения высоты дерева или другого предмета по лужице или зеркальцу.

По лужице, зеркальцу илигелиографу высоту дерева или любого другого предмета на местности, можно измерять следующим образом. Станьте так, чтобы лужица поместилась между вами и деревом (В). Найдите точку, из которой видна отраженная в воде вершина дерева. Измеряемоедерево будет во столько раз выше вас, во сколько расстояние от него до лужицы (ВО) больше расстояния от лужицы до вас (АО). Вместо лужицы также можно воспользоваться зеркальцем, положив его горизонтально так, чтобы увидеть вершину дерева.

Способ определения высоты дерева или другого предмета с помощью прямоугольного треугольника с двумя острыми углами по 45 градусов.

С помощью прямоугольного треугольника с двумя острыми углами по 45 градусов, высоту дерева или другогопредмета определяют так. Отходя от дерева на некоторое расстояние и прикладывая треугольник к глазам так, чтобы один из его катетов был параллелен оси дерева, второй — параллелен земной поверхности, а гипотенуза представляла собой линию визирования.

Затем добиваются такого положения, чтобы линия визирования прошла через вершину дерева. В этом случае высота дерева D равна расстоянию от наблюдателя до дерева и плюс рост наблюдателя.

По материалам книги «Карта и компас мои друзья».
Клименко А.И.

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Подобные треугольники
Практические приложения подобия треугольников
Измерительные работы на местности

Свойства подобных треугольников могут быть использованы при проведении различных измерительных работ на местности.

Определение высоты предмета

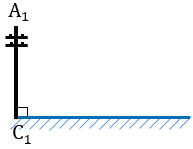
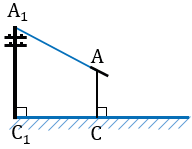
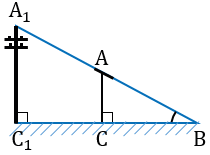
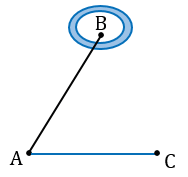
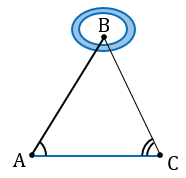
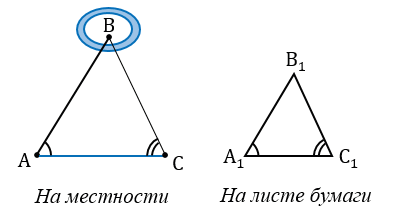
Пусть нам нужно определить высоту телеграфного столба А₁С₁.

Для этого на некотором расстоянии от столба ставим шест АС с вращающейся планкой и направляем планку на верхнюю точку столба А₁.

Далее отмечаем на поверхности земли точку В, в которой прямая А₁А пересекается с поверхностью земли.

В А₁С₁В и АСВ: С₁ =С = 90⁰, В – общий, следовательно, А₁С₁ВАСВ (по 1 признаку подобия треугольников), поэтому сходственные стороны треугольников А₁С₁В и АСВ пропорциональны: , откуда .

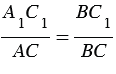
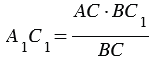
Измерив расстояния ВС₁ и ВС, зная длину шеста АС, по полученной формуле вычисляем высоту А₁С₁ телеграфного столба. Пусть, например, ВС₁ = 6,3 м, ВС = 2,1 м, АС = 1,7 м, тогда: 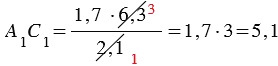м.

Определение расстояния до недоступной точки

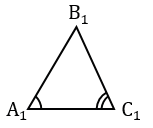
Пусть, нам нужно найти расстояние от пункта А до недоступного пункта В.

Для этого на местности выбираем точку С, провешиваем отрезок АС и измеряем его.

Затем с помощью астролябии измеряем углы А и С.

На листе бумаги строим какой-нибудь треугольник А₁В₁С₁, у которого А₁ =А и С₁ =С. Для того, чтобы построить на листе бумаги углы А₁ и С₁ используем транспортир.

А₁В₁С₁АВС (по 1 признаку подобия треугольников). Из подобия треугольников А₁В₁С₁ и АВС следует, что сходственные стороны данных треугольников пропорциональны: , откуда .

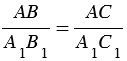
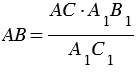
Измерив при помощи линейки длину отрезков А₁В₁ и А₁С₁, зная расстояние АС, по полученной формуле вычисляем расстояние АВ.

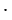
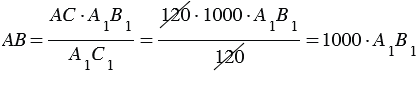
Чтобы сделать вычисления проще, А₁В₁С₁ удобно построить так, чтобы А₁С₁ : АС = 1 : 1000. Например, если АС = 120 м = 1201000 мм (1 м = 1000 мм), то расстояние А₁С₁ берем равным 120 мм. Тогда , поэтому измерив расстояние А₁В₁ в миллиметрах, мы сразу получим расстояние АВ в метрах, т.к. в 1 м = 1000 мм.

Пример:

Пусть АС = 130 м, А = 73⁰, С = 58⁰. На бумаге строим треугольник А₁В₁С₁, так, чтобы А₁ = 73⁰, С₁ = 58⁰, А₁С₁ = 130 мм.

Измеряем с помощью линейки отрезок А₁В₁. Он равен 153 мм, поэтому искомое расстояние АВ = 153 м.

Советуем посмотреть:

Задачи на построение

Пропорциональные отрезки

Определение подобных треугольников

Отношение площадей подобных треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Средняя линия треугольника

Пропорциональные отрезки в прямоугольном треугольнике

Практические приложения подобия треугольников

О подобии произвольных фигур

Синус, косинус и тангенс острого угла прямоугольного треугольника

Значение синуса, косинуса и тангенса для углов 30, 45 и 60

Подобные треугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 579,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 580,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 581,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 582,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 583,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Как определить высоту предмета

Авторы
Руководители
Файлы работы
Наградные документы

Цветов А.Э. 1

1МБОУ СШ №16 г.Павлово Нижегородской области

Захарова Т.Н. 1

1МБОУ СШ №16 г.Павлово Нижегородской области

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Геометрия – одна из древнейших наук, возникших еще до нашей эры. В переводе с греческого слово «геометрия» означает «землемерие». Это название объясняется тем, что его происхождение было связано с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, строительстве зданий и различных сооружений. Другими словами, геометрия возникла из практической деятельности людей и в начале своего развития служила главным образом практическим целям. [6]

На уроках геометрии в 8-м классе при изучении темы «Подобные треугольники» я заинтересовался ее практическим применением, в частности использованием подобия при измерении высоты объекта.

Выбранная тема актуальна тем, что можно узнать, как определить высоту объекта без каких-либо специальных технических устройств. В частности, иногда туристам нужно оценить размер дерева, чтобы построить мост через быструю реку. У них нет под рукой высотомера. Чтобы определить, достаточно ли высоты дерева, чтобы упав, оно перекрыло реку, можно использовать предметы, которые всегда под рукой. Или, например, на садовом участке растет дерево, которое мешает по каким – то причинам. Прежде чем его спилить, нужно решить проблему – не достанет ли оно при падении до любого строения, находящегося рядом с ним. И тут снова на помощь приходят различные методы определения высоты дерева с помощью подручных средств.

Проблема: как определитьвысоту предмета с помощью подручных средств.

Цель исследования: определение высоты предмета различными способами.

Объект исследования: дом, в котором я живу.

Предмет исследования: высота дома.

Задачи:

– рассмотреть различные способы измерения высоты предмета;

– экспериментально проверить использование различных способов определения высоты предмета, определив высоту дома, в котором я живу;

– проанализировать полученные данные и определить наиболее точный способ измерения высоты предмета.

Методы исследования:

– изучение литературы и ресурсов Интернет;

– эксперимент;

– сравнение;

– анализ.

Глава I. Способы определения высоты предмета

В своей профессиональной деятельности строители, архитекторы, лесоводы, военные для определения высоты предмета используют специальные сложные и дорогостоящие приборы – высотометры. В книге Я.И.Перельмана «Занимательная геометрия» [5], а также на сайте «Лесная промышленность» [7] можно найти различные способы определения высоты предмета с помощью подручных средств на примере определения высоты дерева.

В школьных учебниках геометрии также есть практические задачи на определение высоты дерева. Например, в учебнике Л.С.Атанасяна «Геометрия 7-9» [1] в №581 рассмотрен способ измерения высоты дерева с помощью зеркала, а в учебнике А.Г.Мерзляка «Геометрия – 8» [4] в №472 – с помощью тени (рис.1).

рис.1

Изучив литературу [3] и ресурсы сети Интернет, я выделил несколько способов определения высоты предмета и разработал пошаговые инструкции по применению каждого из них на примере измерения высоты дерева.

1. Подобие треугольников

Способы определения высоты предмета с помощью подручных средств основаны на применении такого важного понятия геометрии, как подобие треугольников. [2]

Два треугольника называются подобными, если их углы соответственно равны, и стороны одного треугольника пропорциональны соответственным сторонам другого треугольника (рис.2)

рис.2

Соответственные стороны – это стороны, лежащие напротив равных углов.

Коэффициент подобия – это число k, равное отношению соответственных сторон (рис.3).

рис.3

При решении задач на местности чаще всего применяют первый признак подобия треугольников: если два угла одного треугольника равны соответственно двум углам другого треугольника, то такие треугольники подобны (рис.4).

рис.4

2. Определение высоты с помощью тени

Этот способ называется способом Фалеса. В честь греческого мудреца Фалеса Милетского, который еще за шесть веков до нашей эры научил египтян определять высоту пирамиды по длину ее тени.

Инструкция:

1.Встаньте рядом с деревом так, чтобы были видны тени и дерева, и человека (рис.5).

2.Измерьте тень человека и тень дерева.

3.Измерьте рост человека.

рис.5

Геометрическая постановка задачи. Рассмотрите подобные по двум углам треугольники АВС и А₁В₁С₁ (рис.5) и составьте отношение соответственных сторон , где АВ – искомая высота дерева, А₁В₁– рост человека, ВС – длина тени дерева, В₁С₁ – длина тени человека. Подставьте измерения и найдите величину АВ. Это и будет искомая высота дерева.

3. Определение высоты с помощью равнобедренного прямоугольного треугольника

Инструкция:

1.Держа равнобедренный прямоугольный треугольник на уровне глаз вертикально, отойдите от дерева на такое расстояние, чтобы, глядя вдоль гипотенузы, видно было верхушку дерева (рис.6).

2.Измерьте расстояние от места измерения до дерева.

3.Измерьте катет треугольника.

4.Измерьте рост человека до уровня глаз.

рис.6

Геометрическая постановка задачи. Рассмотрите подобные по двум углам треугольники АВС и А₁В₁С₁ (рис.5) и составьте отношение соответственных сторон , где АС – расстояние от точки измерения до основания дерева, А₁С₁ – длина катета равнобедренного прямоугольного треугольника, ВС – искомая величина, В₁С₁ – длина катета равнобедренного прямоугольного треугольника (рис.7).

рис.7

Подставьте измерения и найдите величину ВС. К полученной величине прибавьте рост человека до уровня глаз. Это и будет искомая высота дерева.

4. Определение объекта с помощью зеркала

Инструкция:

1.Положить зеркало горизонтально на ровную землю на некотором расстоянии от измеряемого дерева (рис.8).

2.Отойти от зеркала на такое расстояние, чтобы видеть в зеркале верхушку дерева.

3.Измерить расстояние от зеркала до основания дерева и до точки измерения.

рис.8

Затем измеряется расстояние от основания дерева до зеркала и расстояние от зеркала до измерителя.

Геометрическая постановка задачи. Способ основан на законе отражения света. Вершина отражается в точке так, что АВ = В. Из подобия треугольников ВС и СЕD следует, что . В этом отношении необходимо только заменить В равным АВ. Решив пропорцию, найдем высоту дерева АВ (рис.9).

рис.9

5. Определение высоты с помощью булавочного прибора

Булавочный прибор можно изготовить из дощечки и трех булавок. На дощечке или куске коры отмечают три точки – вершины равнобедренного прямоугольного треугольника, и в эти точки втыкают по булавке (рис.10).

рис.10

Инструкция:

1.Держа булавочный прибор на уровне глаз так, чтобы один из катетов треугольника был направлен вниз, отойдите от дерева на такое расстояние, чтобы, глядя на булавки А₁ и С₁, можно увидеть верхушку дерева (рис.11).

2.Измерьте расстояние от основания дерева до точки измерения.

рис.11

Геометрическая постановка задачи. Из подобия треугольников АВС и АВ₁С₁ следует отношение соответственных сторон , где АВ – расстояние от точки измерения до основания дерева, АВ₁ – длина катета равнобедренного прямоугольного треугольника, ВС – искомая величина, В₁С₁ – длина катета равнобедренного прямоугольного треугольника (рис.11).

Решив пропорцию, находим ВС. Для того, чтобы найти высоту дерева, необходимо к этой величине прибавить рост человека до уровня глаз.

6. Определение высоты с помощью фотографии

Инструкция:

1.Сделайте фотографию человека на фоне дерева (рис.12).

2.Измерьте рост человека.

3.Измерьте на фотографии высоту дерева и рост человека.

рис.12

Составьте отношение соответственных сторон:

Подставьте измерения и найдите реальную высоту дерева.

Глава II. Проведение эксперимента

1.Измерение высоты дома, в котором я живу

Разработанные инструкции для определения высоты предмета с помощью подручных средств я решил применить на практике, измерив высоту дома, в котором живу (Приложение 1, рис.13).

1)Измерение высоты дома по его тени (Приложение 1, рис.14).

Такое измерение лучше проводить в солнечные дни.

Необходимое оборудование: рулетка.

Результаты измерения: мой рост – 160 см, длина моей тени – 173 см, длина тени дома – 500 см.