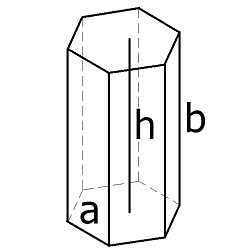
Призма — это многогранник, который состоит из двух одинаковых многоугольников. Они расположены в
разных плоскостях. Призмы различаются по количеству углов в основании. К примеру, если в основании
находится треугольник ,то призма называется треугольной. Если в основании лежит четырехугольник, то
рассматриваемая фигура четырехугольная. Таким образом, фигура, состоящая из 2 равносторонних
треугольников, которые соединены между собой и лежат параллельно друг другу и называется правильная
треугольная призма.
Чтобы было проще понять, рекомендуется начертить на листе бумаге объект 2 равных
параллельных треугольника. Далее соединить их тремя вертикальными чертами. Все стороны у фигуры
обозначаются латинскими буквами, например, «А» «B» «C». Для второго треугольника в призме буквы
дублируются с индексом 1. В результате получается фигура, у которой стороны А₁В₁=В₁С₁=А₁С₁. Призма
АBCА₁В₁С₁ имеет грани в виде параллелограммов. Сторона АА₁ называется боковым ребром. Стороны в
основании геометрической фигуры называются ребрами основания. Высотой в призме называется расстояние
между разными плоскостями.
- Высота правильной треугольной призмы через обьём и ребро
основания - Высота правильной треугольной призмы через площадь боковой
поверхности и ребро основания - Высота правильной треугольной призмы через площадь боковой
поверхности и периметр основания - Высота правильной треугольной призмы через площадь боковой
поверхности и площадь основания - Высота правильной треугольной призмы через площадь грани и
ребро основания - Высота правильной треугольной призмы через диагональ грани
и ребро основания
Через объем и ребро основания
У этой фигуры есть два основания в виде треугольников. Шесть отрезков, которые образуют треугольник в
призме и называют ребрами основания. Длина ребра в правильной призме будет одинаковой, поскольку все
стороны и углы в равностороннем треугольнике равны между собой. Зная это и объем искомого
многоугольника, можно применить эту формулу для осуществления расчетов:
H = 4V / a²√3
где V — объем фигуры измеряется в кубических единицах, а — ребро основания.
Цифр после
запятой:
Результат в:
Длина любой стороны в основании правильной призмы и будет ребром.
Пример.
Если V = 6 мм³, а = 6 мм то расчет неизвестной величины по формуле будет производиться следующим
образом: H = 46 / 6²√3= 24 / 6² * 1.732 = 0,38 мм. Таким образом, применив
формулу, можно узнать высоту через ребро основания и объем.
Через площадь боковой поверхности и ребро основания
Для вычисления потребуется знать площадь боковой поверхности, а также ребро основания. Чтобы
рассчитать площадь боковой поверхности, необходимо умножить периметр фигуры на длину бокового ребра.
Она рассчитывается по данной формуле: Sбок = P * I, где P — периметр, I — длина бокового ребра. Зная
площадь основания боковой поверхности и размеры отрезка, можно использовать формулу:
H = Sбок / 3a
где Sбок — площадь боковой поверхности, а — ребро основания.
Цифр после
запятой:
Результат в:
Пример. Для лучшего понимания можно продемонстрировать на конкретной задаче. Если =
7 мм², а = 8 мм то расчет неизвестной величины будет происходить следующим образом: H = 7 / 3 * 8 = 0,29 мм. Используя такой способ, можно узнать H
правильной треугольной призмы.
Через площадь боковой поверхности и периметр основания
Под периметром равностороннего треугольника, который является основанием рассматриваемой фигуры,
понимается сумма всех его длин, а также сторон. Зная, размер одной стороны легко рассчитать
периметр. Найти площадь боковой поверхности можно по формуле рассмотренной выше. После того как
периметр и боковая площадь известны, то необходимо подставить найденное значение в следующую
формулу:
H = Sбок / P
где S — площадь боковой поверхности, P — периметр основания.
Цифр после
запятой:
Результат в:
Пример. Если P = 2 мм, а Sбок = 16 мм² то расчет размеров будет производиться
следующим образом: H = 16 / 2 = 8 м². С помощью такого простого расчета
можно вычислить H искомой фигуры.
Через площадь боковой поверхности и площадь основания
Площадь основания рассчитывается также, как при нахождении S равностороннего треугольника S = 1/2 * ah, но высота в этом случае неизвестна, поэтому придется
воспользоваться другой формулой S = 1/2 * sin α. Как было сказано ранее,
площадь боковой поверхности считается произведением периметра и длины бокового ребра. Найдя искомые
площади, можно работать со следующей формулой для нахождения высоты призмы:
H = Sбок / (3 √(4 * (Sосн /√3)))
где Sбок — площадь боковой поверхности, Sосн — площадь основания геометрической фигуры.
Цифр после
запятой:
Результат в:
Пример. Если Sбок = 10 мм², а Sосн = 15 мм² то расчет размеров проводится следующим
образом: H = 10 / 3√4 * 15 / √3 = 0.5 мм. Таким образом, используя этот
метод расчета, можно найти H.
Через диагональ грани и ребро основания
Под диагональю грани понимается луч, которые проходит между двумя вершинами, которые находятся на
разных основаниях треугольной призмы. Когда известна диагональ грани, а также размер ребра в
основании, можно решить задачу по этой формуле:
H = √(d² — a²)
где d — диагональ грани, а — ребро основания.
Цифр после
запятой:
Результат в:
Пример. Если d=9 мм², а = 5 мм то расчет искомого параметра по формуле будет
выглядеть следующим образом: H = √(9² — 5²) = 7.4 мм. Таким образом,
используя эту формулу, можно вычислить H.
Через площадь грани и ребро основания
Ребро основания равняется длине любого отрезка в равностороннем треугольнике внутри призмы. Граней у
призмы 3. Две боковые и одна задняя. Они изображены в виде параллелограммов. Зная длину и площадь
грани у призмы, можно воспользоваться следующую формулу для расчета высоты правильной треугольной
призмы:
H = S / a
где S — площадь грани, a — ребро основания.
Цифр после
запятой:
Результат в:
Пример. Если S = 5 мм², а = 8 мм² то вычисления H будут производиться следующим
способом: H = 5 / 8 = 0,62 мм. С помощью этой формулы можно найти искомую
величину.
Умение рассчитать высоту треугольного многогранника пригодится при решении геометрических задач.
Знания могут потребоваться в школе, в университете, но иногда такая необходимость может возникнуть в
реальной жизни. Например, как строитель сможет посчитать площадь дома в виде призмы, если не знает
расчетной формулы. Важно понимать, как найти неизвестные переменные, когда известно лишь несколько
параметров.
Download Article
Download Article
A prism is a three-dimensional solid with two parallel bases, or faces, that are congruent.[1]
The shape of the base determines what type of prism you have, such as a rectangular or triangular prism. Because it is a 3D shape, finding the volume (space inside) of a prism is a common task; however, sometimes you will need to find the height of a prism. Finding the height is possible if you have enough information already given: either the volume, or the surface area and perimeter of the base. The formulas described in these methods can work for prisms with bases of any shape, provided you know the formula for finding the area of that shape.
-
1
-
2
Plug the volume into the formula. If you do not know the volume, you cannot use this method.
Advertisement
-
3
Find the area of the base. To find the area, you need to know the length and width of the base (or of one side, if the base is a square). Use the formula
. To find the area of a rectangle.[3]
-
4
Plug the area of the base into the volume of a prism formula. Make sure you are substituting for the variable
.
- For example, if you found the area of the base to be 16 square meters, then your formula will look like this:
- For example, if you found the area of the base to be 16 square meters, then your formula will look like this:
-
5
Solve the equation for
. This will give you the height of your prism.
Advertisement
-
1
-
2
Plug the volume into the formula. If you do not know the volume, you cannot use this method.
-
3
Find the area of the base. To find the area, you need to know the length of the triangle’s base and the height of the triangle. Use the formula
to find the area of a triangle.[5]
-
4
Plug the area of the base into the volume of a prism formula. Make sure you are substituting for the variable
.
- For example, if you found the area of the base to be 42 square meters, then your formula will look like this:
- For example, if you found the area of the base to be 42 square meters, then your formula will look like this:
-
5
Solve the equation for
. This will give you the height of your prism.
Advertisement
-
1
-
2
Plug the surface area of the prism into the formula. If you do not know the surface area, this method will not work.
- For example, if you know the surface area is 1460 square centimeters, your formula will look like this:
- For example, if you know the surface area is 1460 square centimeters, your formula will look like this:
-
3
Find the area of the base. To find the area, you need to know the length and width of the base (or of one side, if the base is a square). Use the formula
. To find the area of a rectangle.[7]
-
4
Plug the area of the base into the formula for the surface area of a prism and simplify. Make sure you are substituting for the letter
.
-
5
Find the perimeter of the base. To find the perimeter of a rectangle, add up the length of all four sides, or, for a square, multiply the length of one side by 4.
-
6
Plug the perimeter of the base into the formula for the surface area of a prism. Make sure you are substituting for the letter
.
- For example, if you found the perimeter of the base to be 20, your formula will look like this:
- For example, if you found the perimeter of the base to be 20, your formula will look like this:
-
7
Solve the equation for
. This will give you the height of your prism.
Advertisement
-
1
-
2
Plug the surface area of the prism into the formula. If you do not know the surface area, this method will not work.
- For example, if you know the surface area is 1460 square centimeters, your formula will look like this:
- For example, if you know the surface area is 1460 square centimeters, your formula will look like this:
-
3
Find the area of the base. To find the area, you need to know the length of the triangle’s base and the height of the triangle. Use the formula
. To find the area of a triangle.[9]
-
4
Plug the area of the base into the formula for the surface area of a prism and simplify. Make sure you are substituting for the letter
.
-
5
Find the perimeter of the base. To find the perimeter of a triangle, add up the length of all three sides.
-
6
Plug the perimeter of the base into the formula for the surface area of a prism. Make sure you are substituting for the letter
.
- For example, if you found the perimeter of the base to be 21, your formula will look like this:
- For example, if you found the perimeter of the base to be 21, your formula will look like this:
-
7
Solve the equation for
. This will give you the height of your prism.
Advertisement
Add New Question
-
Question
How do I find the height of a cylinder given the volume?
You can use Method 1 and the formula V = Ah. The base of a cylinder is a circle, so A will equal the area of the circle, which is pi x r^2. As long as you know the radius of the circle, you should be able to solve for h.
-
Question
How can I find the height of a rectangular prism with the width, length and area of base?
You also need to know the volume, in which case, you would divide the volume by the area.
-
Question
How do I find the width of a rectangular prism?
Assuming you know the volume, divide the volume by the height, then divide by the length.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
Things You’ll Need
- Pen/pencil and paper or calculator (optional)
References
About This Article
Article SummaryX
To find the height of a rectangular prism with a known volume, use the formula V=Ah, where V equals volume, A equals the area of one side, and h equals height. If you don’t have the area, multiply the width and length of one side to get that value. For triangular prisms with a known value, you use the same formula V=AH, but finding the area of one side is different. Use the formula A = 1/2bh, where b equals base and h equals height to get the area so you can solve for the height of the prism. To learn how to find the height of a triangular prism using the surface area, scroll down!
Did this summary help you?
Thanks to all authors for creating a page that has been read 378,388 times.
Did this article help you?
Загрузить PDF
Загрузить PDF
Призма – это объемная фигура с двумя равными параллельными основаниями.[1]
Фигура в основании определяет тип призмы, например, прямоугольная или треугольная призма. Так как призма является объемной фигурой, зачастую нужно вычислить объем (пространство, ограниченное боковыми гранями и основаниями) призмы. Но иногда в задачах требуется найти высоту призмы. Это не так сложно, если дана необходимая информация: объем или площадь поверхности и периметр основания. Формулы, приведенные в этой статье, применимы к призмам с основаниями любой формы, если знать, как вычислить площадь основания.
-
1
-
2
В формулу подставьте объем. Если объем не дан, этот метод использовать нельзя.
- Пример: объем призмы равен 64 кубических метров (м3); формула запишется так:
- Пример: объем призмы равен 64 кубических метров (м3); формула запишется так:
-
3
Вычислите площадь основания. Для этого нужно знать длину и ширину основания (или одну из сторон, если основание представляет собой квадрат). Чтобы вычислить площадь прямоугольника, воспользуйтесь формулой
.
-
4
Подставьте площадь основания в формулу для вычисления объема призмы. Значение площади подставьте вместо
.
- Пример: площадь основания равна 16 м2, поэтому формула запишется так:
- Пример: площадь основания равна 16 м2, поэтому формула запишется так:
-
5
Найдите
. Так вы вычислите высоту призмы.
Реклама
-
1
-
2
В формулу подставьте объем. Если объем не дан, этот метод использовать нельзя.
- Пример: объем призмы равен 840 кубических метров (м3); формула запишется так:
- Пример: объем призмы равен 840 кубических метров (м3); формула запишется так:
-
3
Вычислите площадь основания. Для этого нужно знать высоту треугольника и сторону, на которую опущена высота. Чтобы вычислить площадь треугольника, воспользуйтесь формулой
.
-
4
Подставьте площадь основания в формулу для вычисления объема призмы. Значение площади подставьте вместо
.
- Пример: площадь основания равна 42 м2, поэтому формула запишется так:
- Пример: площадь основания равна 42 м2, поэтому формула запишется так:
-
5
Найдите
. Так вы вычислите высоту призмы.
Реклама
-
1
-
2
В формулу подставьте площадь поверхности. Если площадь поверхности не дана, этот метод использовать нельзя.
- Пример: площадь поверхности призмы равна 1460 квадратных сантиметров; формула запишется так:
- Пример: площадь поверхности призмы равна 1460 квадратных сантиметров; формула запишется так:
-
3
Вычислите площадь основания. Для этого нужно знать длину и ширину основания (или одну из сторон, если основание представляет собой квадрат). Чтобы вычислить площадь прямоугольника, воспользуйтесь формулой
.
-
4
Подставьте площадь основания в формулу для вычисления площади поверхности призмы. Значение площади подставьте вместо
.
-
5
Найдите периметр основания. Чтобы найти периметр прямоугольника, сложите значения всех (четырех) сторон; чтобы найти периметр квадрата, умножьте значение одной стороны на 4.
-
6
Подставьте периметр основания в формулу для вычисления площади поверхности призмы. Значение периметра подставьте вместо
.
- Пример: если периметр основания равен 20, формула запишется так:
- Пример: если периметр основания равен 20, формула запишется так:
-
7
Найдите
. Так вы вычислите высоту призмы.
Реклама
-
1
-
2
В формулу подставьте площадь поверхности. Если площадь поверхности не дана, этот метод использовать нельзя.
- Пример: площадь поверхности призмы равна 1460 квадратных сантиметров; формула запишется так:
- Пример: площадь поверхности призмы равна 1460 квадратных сантиметров; формула запишется так:
-
3
Вычислите площадь основания. Для этого нужно знать высоту треугольника и сторону, на которую опущена высота. Чтобы вычислить площадь треугольника, воспользуйтесь формулой
.
-
4
Подставьте площадь основания в формулу для вычисления площади поверхности призмы. Значение площади подставьте вместо
.
-
5
Найдите периметр основания. Чтобы найти периметр треугольника, сложите значения всех (трех) сторон.
-
6
Подставьте периметр основания в формулу для вычисления площади поверхности призмы. Значение периметра подставьте вместо
.
- Пример: если периметр основания равен 21, формула запишется так:
- Пример: если периметр основания равен 21, формула запишется так:
-
7
Найдите
. Так вы вычислите высоту призмы.
Реклама
Предупреждения
- Не путайте высоту треугольной призмы с высотой треугольника, который лежит в основании призмы. Высота треугольника – это перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону, которая называется основанием треугольника. Высоту равнобедренного треугольника можно найти, если дано основание и боковая сторона. Разделите основание на 2, а затем воспользуйтесь теоремой Пифагора (
), где а (или b) – высота треугольника. Запомните: апофемы в призме нет!
Реклама
Что вам понадобится
- Ручка/карандаш и бумага или калькулятор (необязательно)
Об этой статье
Эту страницу просматривали 99 619 раз.
Была ли эта статья полезной?
Виды призм
-
Прямая призма – это призма, в которой все боковые грани перпендикулярны к основанию. Высота равна длине бокового ребра. -
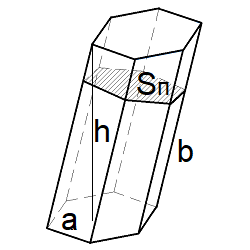
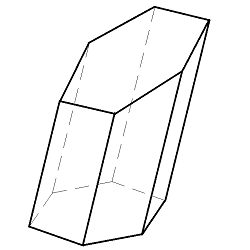
Наклонная призма – это призма, в которой боковые грани не перпендикулярны к основанию. -
Правильная призма – это призма, в которой основания являются правильными многоугольниками. Правильная призма может быть, как прямой, так и наклонной. -
Усечённая призма – это призма, в которой основания не параллельны друг другу. Усечённая призма может быть, как прямой, так наклонной.
Основные свойства призмы
- Основание призмы – равные многоугольники
- Высота прямой призмы равна длине бокового ребра.
- Боковые ребра призмы параллельны и равны между собой.
- Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням.
- Боковые грани призмы – параллелограммы
- Высота наклонной призмы всегда меньше длины ребра.
- В прямой призме грани могут быть прямоугольниками или квадратами.
Площадь основания правильной призмы
$$
S_{осн} = {N * a^2 over 4 * tan(180/N)}
$$
| Где: | N – количество сторон у основания пирамиды |
Формулы объёма призмы
Объём призмы через площадь основания (SОСН) и высоту (h):
$$
V = S_{ОСН} * h
$$
Объём наклонной призмы через площадь перпендикулярного сечения (SП) и длину бокового ребра (b):
$$
V = S_П * b
$$
Объём правильной прямой призмы через высоту, длину стороны и количество сторон:
$$
V = {N over 4} * h * a * ctg({pi over N})
$$
| Где: | N – количество сторон у основания пирамиды |
| h – высота призмы | |
| a – длина стороны основания призмы |
Формулы площади поверхности правильной призмы
Площадь боковой поверхности призмы через периметр (P) основания и высоту (h)
$$
S_Б = P * h
$$
Площадь поверхности призмы через площадь основания (SОСН), периметр основания (P) и высоту (h):
$$
S = 2 * S_{ОСН} + P * h
$$
Площадь поверхности правильной призмы через высоту, длину стороны и количество сторон:
$$
S = {N over 2} * a^2 * ctg({pi over N}) + N * a * h
$$
| Где: | N – количество сторон у основания пирамиды |
| h – высота призмы | |
| a – длина стороны основания призмы |
Объемное тело, в основании которого лежит многоугольник, называется призмой. У стандартной призмы оба основания конгруэнтны, что значит, что все их стороны и углы соответственно равны. Призма может быть прямой и наклонной, в прямой призме все отрезки, соединяющие соответствующие вершины оснований, перпендикулярны им и равны между собой, а также совпадают по значению с высотой. Эти отрезки, называемые боковыми ребрами, образуют со сторонами основания прямоугольники, которые будут конгруэнтны между собой в случае призмы с правильным многоугольником в основании. Таким образом, зная сторону многоугольника в основании и площадь боковой поверхности призмы, можно найти высоту по следующей формуле, где a – это сторона основания, а n – их количество:
Так как высота призмы прямо пропорционально связана с ее объемом, то использование этого отношения и есть самый простой и быстрый способ ее нахождения, и это актуально и для наклонных призм в том числе. Итак, чтобы вычислить высоту призмы через объем необходимо конвертировать формулу объема призмы таким образом, чтобы высота стала неизвестным параметром. Тогда она примет значение отношения объема к площади основания призмы: