Призма, вписанная в цилиндр.
Призму называют вписанною в цилиндр, если её основания
вписаны в основания цилиндра, а боковые рёбра касательные цилиндра.
При этом цилиндр называют описанным вокруг призмы. Понятно,
что если касательные цилиндра перпендикулярны к плоскости основания, то призма,
вписанная в цилиндр, будет прямою.
Из определения призмы, вписанной в цилиндр, вытекают её
свойства:
– цилиндр можно описать вокруг прямой призмы, если её
основанием является многогранник, вокруг которого можно описать окружность; при этом радиус цилиндра R равен радиусу этой
окружности;
– высота Н призмы, которая
соединяет центры окружностей, описанных вокруг основ, принадлежит оси цилиндра.
Формулы вычисления радиуса R описанной окружности.
Где a, b, с – стороны, h – высота, d – диагональ.
ПРИМЕР:
Можно или нет описать цилиндр вокруг
прямой призмы, в основании которой лежит треугольник ?
РЕШЕНИЕ:
Да, так как вокруг любого треугольника
можно описать окружность.
ПРИМЕР:
Можно или нет описать цилиндр вокруг
прямой призмы, в основании которой лежит ромб, если он не является квадратом ?
РЕШЕНИЕ:
Нет, так как вокруг ромба, который
не является квадратом, нельзя описать окружность.
Призма, описанная вокруг цилиндра.
Касательной плоскостью цилиндра называют плоскость, которая
проходит через касательную цилиндра и перпендикулярная к плоскости осевого сечения,
в котором находится касательная цилиндра.
Призму называют описанной вокруг цилиндра, если её
основания описаны вокруг оснований цилиндра, а боковые грани принадлежат плоскостям,
которые касаются цилиндра.
При этом цилиндр называют вписанным в призму, так как касательные
цилиндра перпендикулярные к плоскости оснований, и боковые грани призмы, в
которых находятся касательные, также перпендикулярные к плоскости оснований, то
есть призма, описанная вокруг цилиндра, будет прямой.
По определению призмы, описанной вокруг цилиндра, определим
её свойства:
– цилиндр можно вписать в прямую призму, если её основания
будут многогранники, в которые можно вписать окружности; при этом радиус цилиндра r равен радиусу этой
окружности;
– высота Н призмы, которая
соединяет центры окружностей, вписанных в основания, принадлежит оси цилиндра.
Формулы вычисления радиуса r описанной окружности.
Где h – высота, S – площадь, р – полупериметр, a – сторонa.
ЗАДАЧА:
Вокруг цилиндра, высота которого равна 5 см, описали четырёхугольную
призму, три стороны которой в порядке следования равны
3 см, 4 см и 7 см.
Найти площадь
боковой поверхности призмы.
РЕШЕНИЕ:
Обозначим неизвестную сторону четырёхугольника
основания х. Так как этот четырёхугольник описан вокруг окружности, то
3 + 7 = 4 + х,
откуда х = 6 см.
Площадь боковой поверхности призмы
Sбок = P × l
где, Р – периметр
основания,
l – боковое ребро, которое равно высоте цилиндра.
Имеем:
Р = 3 + 7 + 4 +
6 = 20 (см).
Sбок = 20 × 5 = 100 (см2).
ОТВЕТ: 100 см2.
ЗАДАЧА:
В цилиндр вписана правильная
шестиугольная призма. Найдите угол между диагональю её боковой грани и осью
цилиндра, если радиус основания равен высоте цилиндра.
РЕШЕНИЕ:
Из условия задачи имеем:
В цилиндр вписана правильная
шестиугольная призма. Радиус основания цилиндра равен высоте призмы АО = АА1.
Боковые грани – квадраты, так как сторона правильного шестиугольника,
вписанного в окружность, равна радиусу. Рёбра призмы параллельны оси цилиндра,
поэтому угол между диагональю грани и осью цилиндра равен углу между диагональю
и боковым ребром. А этот угол равен 45°, так как грани – квадраты.
ЗАДАЧА:
Правильная
четырёхугольная призма описана около цилиндра, радиус основания которого
равен 0,5. Площадь боковой
поверхности призмы равна 8. Найдите высоту цилиндра.
РЕШЕНИЕ:
Так как четырёхугольная призма правильная, то в
основании лежит квадрат.
Радиус окружности, вписанной в квадрат, равен 0,5.
Следовательно, сторона квадрата равна диаметру окружности, то есть
2 ∙ 0,5 = 1.
Так как все боковые грани призмы равны, то площадь одной
грани равна
8 : 4 = 2.
Каждая грань представляет собой прямоугольник,
следовательно, её площадь равна произведению бокового ребра призмы на сторону
основания (квадрата). Следовательно, боковое ребро призмы равно:
2 : 1 = 2.
Высота цилиндра равна боковому ребру призмы,
следовательно, она равна 2.
ЗАДАЧА:
В цилиндр вписан правильный параллелепипед. Найдите
площадь полной поверхности этого параллелепипеда, если радиус цилиндра 10
см, а высота 20
см.
РЕШЕНИЕ:
Пусть О и О1 – центры основ данного цилиндра,
ОО1 – отрезок оси цилиндра, являющийся высотой. Поскольку параллелепипед
вписан в цилиндр, то его основания – параллелограммы. АВСD и А1В1С1D1, вписанные в основания цилиндра, следовательно, они прямоугольники или
квадраты, причем точки О и О1 – центры этих четырехугольников – точки пересечения диагоналей. Тогда
АА1 ∥ ВВ1 ∥ СС1 ∥ DD1 ∥ ОО1.
ОО1 ⊥ (АВС),
ОО1 ⊥ (А1В1С1),
следовательно, параллелепипед является
прямоугольным. Диагонали четырехугольников являются диаметрами цилиндра,
боковые ребра – образующие цилиндра,
Поскольку параллелепипед
правильный, то АВСD – квадрат,
АО = ВО = СO = DО = R = 10 см,
тоді АВ = 10√͞͞͞͞͞2 см.
Sп
= Sб
+ 2Sосн = P∙
H + 2SABCD
=
= 4
∙ 10√͞͞͞͞͞2 ∙
20 +
2(10√͞͞͞͞͞2)2 =
= 800√͞͞͞͞͞2 +
400 = 400(2√͞͞͞͞͞2 +
1)
(см2).
ОТВЕТ: 400(2√͞͞͞͞͞2 +
1) см2
ЗАДАЧА:
Вокруг цилиндра описана правильная четырёхугольная
призма, площадь боковой поверхности которой равна Q. Найдите площадь боковой поверхности
цилиндра.
РЕШЕНИЕ:
Если правильная четырехугольная призма описана вокруг
цилиндра, то круги основания цилиндра, вписанные в основания призмы, –
квадраты, центры оснований цилиндра – точки пересечения диагоналей квадратов,
боковое ребро призмы равно образующей цилиндра и является высотой призмы и
цилиндра. Отметим сторону квадрата а, радиус цилиндра r, высоту призмы и цилиндра Н.
По условию
Sб.пр. = Q,
Sб.пр. = P∙ H = 4a ∙ H = Q,
Sб.ц. = 2πrH, а = 2r.
Маємо:
4a ∙ H = Q, 4∙ 2rH = Q, 2rН = Q/4,
тоді
Sб.ц. = π ∙ 2RH = π∙ Q/4
ВІДПОВІДЬ: π∙ Q/4
Решение задач с применением
тригонометрии.
ЗАДАЧА:
В цилиндр вписана треугольная призма, основанием которой
является прямоугольный треугольник с катетом
а и прилежащим к нему острым углом α.
Диагональ грани призмы, в которой находится эта сторона треугольника, наклонена
к плоскости основания под углом β.
Найдите площадь боковой поверхности цилиндра.
РЕШЕНИЕ:
Пусть на рисунке изображен данный цилиндр,
О и О1 – центры оснований, ОО1 –
отрезок оси цилиндра, являющийся высотой. В данный цилиндр вписана треугольная
призма (прямая).
АВСА1В1С1, ∠ С = ∠ С1 = 90°.
Тогда ∆ АВС и ∆
А1В1С1 вписаны в круги оснований цилиндра, О и О1 –
середины гипотенуз АВ и А1В1, боковые ребра призмы являются образующими цилиндра,
∠ ВАС = α, АС = а,
АА1 ∥
ВВ1 ∥ СС1 ∥ DD1,
АА1 ⊥ (АВС),
А1С –
наклонная, АС – проекция,
поэтому ∠ АСА1 = β – угол между
А1С и (АВС).
ВІДПОВІДЬ:
Задания к уроку 12
Цилиндр называется описанным около призмы, если многоугольники оснований призмы вписаны в окружности оснований цилиндра, а образующие цилиндра являются боковыми рёбрами призмы.


Цилиндр можно описать только около такой прямой призмы, около основания которой можно описать окружность.
Например, цилиндр всегда можно описать около прямой треугольной призмы, около правильной призмы.
Рисунок составляется в зависимости от содержания задания, часто достаточно рисунка основания комбинаций этих тел, т. к. высота призмы равна высоте цилиндра.
Окружность основания цилиндра описана около многоугольника основания призмы.
Радиус цилиндра — это радиус окружности, описанной около многоугольника основания призмы.
Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника.
Центр окружности, описанной около четырёхугольника, является точкой пересечения серединных перпендикуляров к сторонам четырёхугольника. Около четырёхугольника можно описать окружность, если суммы противоположных углов равны
180°
.
Формулы вычисления радиуса (R) описанной окружности
(a, b, c) — стороны, (h) — высота, (d) — диагональ.
| Правильный треугольник | (R =) 23h; (R=) a33 |
| Прямоугольный треугольник | (R=) 12 гипотенузы |
| Произвольный треугольник | R=abc4S;R=a2sinα |
| Квадрат |
(R =) a22 |
|
Прямоугольник |
(R =) d2 |
|
Правильный шестиугольник |
(R = a) |
Цилиндр вписан в призму, если окружности оснований цилиндра вписаны в многоугольники оснований призмы.

Цилиндр можно вписать только в такую прямую призму, в многоугольник основания которой можно вписать окружность.
Например, цилиндр всегда можно вписать в прямую треугольную призму, в правильную призму.
Рисунок создаётся в зависимости от содержания задачи, часто достаточно нарисовать основание комбинаций этих тел, т. к. высота цилиндра равна высоте призмы.
Окружность основания цилиндра вписана в многоугольник основания призмы.
Радиус цилиндра — радиус окружности, вписанной в многоугольник основания призмы.
Центр вписанной в треугольник окружности находится в точке пересечения биссектрис треугольника.
Центр окружности, вписанной в четырёхугольник, находится в точке пересечения биссектрис четырёхугольника. В четырёхугольник можно вписать окружность, если равны суммы длин противоположных сторон.
Формулы вычисления радиуса (r) вписанной окружности
Где (h) — высота, (S) — площадь, (p) — полупериметр, (a) — сторона.
| Правильный треугольник | r=13h;r=a36 |
| Произвольный (и прямоугольный) треугольник | (r =) Sp |
| Квадрат | |
| Ромб |
или |
| Правильный шестиугольник | (r =) a32 |
Геометрия, 11 класс
Урок №12. Объемы прямой призмы и цилиндра
Перечень вопросов, рассматриваемых в теме
1) Доказательство теорем об объемах прямой призмы и цилиндра
2) Определение призмы, вписанной в цилиндр и призмы описанной около цилиндра
3) Решение задач на нахождение объемов прямой призмы и цилиндра
V=Sh объем прямой призмы и цилиндра
Основная литература:
Бутузов В. Ф., Кадомцев С. Б., Атанасян Л. С. и др. Геометрия. 10–11 классы : учеб.для общеобразоват. организаций : базовый и углубл. Уровни – М.: Просвещение, 2014. – 255, сс. 121-126.
Дополнительная литература:
Шарыгин И.Ф. Геометрия. 10–11 кл.: учеб.для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.
Потоскуев Е.В., Звавич Л. И., Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.
Открытые электронные:
Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177
Теоретический материал для самостоятельного изучения
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Прямая призма — это призма, у которой боковые ребра перпендикулярны плоскости основания, откуда следует, что все боковые грани являются прямоугольниками
Объем всякого цилиндра равен произведению площади основания на высоту
Объем призмы — это произведение площади ее основания на высоту
Призма вписана в цилиндр, если ее основания вписаны в основания цилиндра.
Призма описана около цилиндра, если ее основания описаны около оснований цилиндра.
Высота любой призмы (вписанной в цилиндр или описанной около цилиндра), равна высоте самого цилиндра
Примеры и разбор решения заданий тренировочного модуля
№1. Найти объем прямой треугольной призмы высотой 6, в основании которой – прямоугольный треугольник с катетами 3 и 7.
Решение: Объем призмы вычисляется по формуле , т.к. в основании призмы – прямоугольный треугольник, то объем призмы будет вычисляться по формуле
, где а и в – катеты треугольника. Подставляя все данные задачи в формулу, получаем ответ:
.
№2. Найти объём правильной -угольной призмы, у которой каждое ребро равно а, если: а) n=3, б) n=4, в) n=6.
Решение: поскольку призма правильная, значит, это прямая призма и в основании лежит правильный многоугольник.
Формулу для вычисления объёма прямой призмы мы только что вывели 
Основанием правильной треугольной призмы является правильный, то есть равносторонний треугольник n=3. Площадь правильного треугольника со стороной f вычислить несложно, она равна 
Применяя формулу для вычисления объёма прямой призмы, получим, что объём правильной треугольной призмы равен 
Основанием правильной четырёхугольной призмы является квадрат n=4. Площадь квадрата со стороной a равна 

Основанием правильной шестиугольной призмы является правильный шестиугольник n=6. Своими большими диагоналями шестиугольник делится на 6 равносторонних треугольников. Площадь каждого из треугольников равна 


Ответ 3
№3 Найди объём прямой призмы если 
Решение: боковая грань прямой призмы является прямоугольником.
Площадь каждой боковой грани равна произведению высоты призмы на сторону основания.
То есть большая боковая грань содержит большую сторону основания.
По условию
Получим, что длина стороны АС=7см.
Зная большую сторону основания и площадь наибольшей боковой грани призмы, длину высоты призмы вычислить нетрудно.
Получим, что длина высоты призмы равна 
Для нахождения объёма призмы, воспользуемся только что доказанной формулой 


Мы воспользуемся второй формулой. Получим, что площадь основания равна 
Тогда объём прямой призмы равен 
Ответ 75
Тип урока: ознакомление с новым материалом.
Технология урока:
проблемно-исследовательская технология.
Цели урока:
- Рассмотреть понятия: вписанного цилиндра в
призму и вписанной призмы в цилиндр; - Использовать эти понятия при решении задач;
- Формировать представления об использовании
этих понятий в практической жизни человека.
Метапредметные связи: геометрия, черчение,
рабочие профессии.
Учащиеся должны знать:
- Понятия: вписанного цилиндра в призму и
вписанной призмы в цилиндр; - Применение данных понятий при решении задач;
- Применение данных понятий в практической жизни.
Учащиеся должны уметь:
- Решать задачи на взаимное расположение
цилиндра и призмы; - Объяснять применение данных понятий в
практической жизни человека.
План урока:
- Организационный момент (1 минута);
- Постановка проблемы на определение темы урока и
его целей. (3 минуты); - Актуализация знаний учащихся. Повторение ранее
изученного материала (5 минут); - Объяснение новой темы. Проблемно-поисковая
работа.(7 минут); - Закрепление изученных понятий в ходе
фронтального опроса.(7 минут); - Решение задач различного уровня сложности. (15
минут); - Рефлексия. Итоговый тест по усвоению новых
понятий с самопроверкой. (5 минут); - Подведение итогов урока. Домашнее задание.(1
минута).
ХОД УРОКА
1. Постановка проблемы: токарь из
шестигранника вытачивает цилиндр.
Вопрос: о каком взаимном расположении
геометрических тел идет речь? (слайд 1 из презентации к уроку)
Используя определенные инструменты,
фрезеровщик из цилиндрической заготовки
получает шестигранник.
Вопрос:о каком взаимном расположении
геометрических тел идет речь? (слайд 2)
Тема урока “Цилиндр, вписанный в призму.
Призма, вписанная в цилиндр”. (слайд 3)
Цели урока:
- Рассмотреть понятия: вписанного цилиндра в
призму и вписанной призмы в цилиндр; - Использовать эти понятия при решении задач;
- Формировать представления об использовании
этих понятий в практической жизни
человека.(слайд 4)
2. Актуализация знаний учащихся. Повторение
ранее изученного.
Повторение определений, связанных с понятиями
“призма” и “цилиндр”:
- В какой треугольник можно вписать окружность?
Около какого треугольника можно описать
окружность? - В какой четырехугольник можно вписать
окружность? Около какого четырехугольника можно
описать окружность? - Формулы для вычисления площади правильного
многоугольника, его стороны и радиуса вписанной
окружности. Памятка на столе (Приложение
1). - Решить задачу: Найдите боковое ребро правильной
четырехугольной призмы, если сторона ее
основания равна 9 см, а площадь поверхности равна
306 см2. У слабых учащихся лежит на столе
решение этой задачи с пропусками, которые они
должны заполнить во время работы (Приложение
2). - Жестянщик изготавливает 10 баков цилиндрической
формы размерами 50 см в высоту и 40 см в диаметре.
Сколько листов железа размерами 0,81,6 м потребуется для этого (5%
листового железа идет на скрепление деталей)?
Ответ округлите до целых. У слабых учащихся
лежит на столе решение этой задачи с пропусками,
которые они должны заполнить во время работы (Приложение 3).
3. Объяснение новой темы. Проблемно – поисковая
работа.
Как вы думаете можно ли вписать в цилиндр
призму?
При каких условиях призма вписана в цилиндр?
- Призма прямая.
- Основания призмы вписаны в основания
цилиндра. - Боковые ребра призмы совпадают с образующими
(слайд 6).
Как вы думаете можно ли описать около цилиндра
призму?
При каких условиях около цилиндра можно
описать призму?
- Призма прямая.
- Основания цилиндра вписаны в основания
призмы. - Образующие цилиндра совпадают с боковыми
ребрами призмы (слайд 7).
4. Закрепление изученных понятий в ходе
фронтального опроса.
- Можно ли описать цилиндр вокруг прямой призмы, в
основании которой лежит ромб? - Можно ли вписать цилиндр в призму, в основании
которой лежит прямоугольник? - Определите вид треугольника, лежащего в
основании призмы, вписанной в цилиндр, если ось
цилиндра проходит внутри призмы (слайд 8)? - В прямой четырехугольной призме углы основания
в порядке следования относятся как 3:5:8:6. Можно ли
описать цилиндр вокруг этой призмы?
5. Решение задач различного уровня сложности по
готовым чертежам.
В цилиндр вписана правильная шестиугольная
призма, а вокруг него описана правильная
четырехугольная призма.Найти отношение площадей
боковых поверхностей этих призм (слайд 9).
Решение: =
=
= 3/4. Ответ: 3/4.
В основании прямой призмы лежит ромб. Площадь
боковой поверхности призмы равна 120 см2.
Найти радиус основания цилиндра, вписанного в
эту призму, если высота призмы равна 6 см, а острый
угол основания — 60°(слайд 10).
Решение S = Ph = , 120 = 4 * а * 6, а = 5см.
осн = а2 *
,
осн =
25,
осн
= (25):5 =
, r =
:2 =
.
Ответ:
см.
Прямоугольный параллелепипед со сторонами 6дм
и 8дм и высотой, равной 14дм, вписан в цилиндр.
Найдите радиус основания цилиндра, площадь
полной поверхности цилиндра(слайд 11).
Ответ: r=5 дм, S=190 дм2.
Площадь осевого сечения цилиндра равна Q. Найти
площадь боковой поверхности правильной
шестиугольной призмы, описанной вокруг этого
цилиндра (слайд 12).
Ответ: 2Q.
6. Рефлексия. Итоговый тест по усвоению новых
понятий с самопроверкой.
- Верно ли утверждение: в наклонную призму можно
вписать цилиндр? - Верно ли утверждение: высота цилиндра равна
высоте, вписанной в него треугольной призме? - Верно ли утверждение: около любой треугольной
призмы можно описать цилиндр? - Верно ли утверждение: в любую четырехугольную
призму можно вписать цилиндр? - Верно ли утверждение: около правильной
шестиугольной призмы можно описать цилиндр? - Верно ли утверждение: призму высотой 40 см можно
вписать в цилиндр высотой 24 см? - Из тонкостенной цилиндрической трубы жестянщик
делает четырехгранную водосточную трубу. Будут
ли равны площади поверхностей этих труб? - Найдите боковое ребро правильной
четырехугольной призмы, если сторона ее
основания равна 2, а площадь поверхности равна 104. - Люди, каких профессий сталкиваются с понятиями:
“вписанный цилиндр в призму” и “ вписанная
призма в цилиндр”?
Выполнить самопроверку и проанализировать
знания и умения, полученные на уроке (слайд13).
7. Итог урока. Домашнее задание.
Дома № 629.
Литература.
1. Атанасян Л.Г., Бутузов В.Ф., Кадомцев С.Б. и др.
Геометрия 10 – 11. Учебник для общеобразовательных
учреждений. – 15-е изд.,доп. – М.: Просвещение, 2006.
2. Саакян С.М., Бутузов В.Ф. Изучение геометрии в 10
– 11 классах. Метод. рекомендации к учеб.: Кн. для
учителя. – 2-изд. – М. Просвещение, 2003.
Призма вписана в цилиндр, если ее основания — многоугольники, вписанные в основания цилиндра, а боковые ребра являются образующими призмы.
Высоты вписанной призмы и цилиндра равны.
В школьном курсе изучается только прямой круговой цилиндр, соответственно, вписанная в цилиндр призма также должна быть прямой.
Призма может быть вписана в цилиндр, если около ее основания можно описать окружность. Отсюда следует, в цилиндр можно вписать любую правильную призму, прямую треугольную призму, прямоугольный параллелепипед.
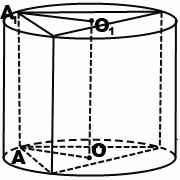
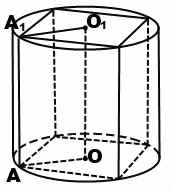
В ходе решения задач на призму, вписанную в цилиндр, можно рассмотреть часть осевого сечения комбинации тел — прямоугольник, стороны которого равны радиусу описанной около основания призмы окружности ( радиусу цилиндра) и высоте призмы (и цилиндра). Например, в прямоугольнике AA1O1O OO1=H — высота призмы и цилиндра, AO=R — радиус описанной окружности.
Найдем отношение объема призмы к объему описанного около нее цилиндра:
В частности, отношение объема правильной треугольной призмы к объему описанного цилиндра
![Rendered by QuickLaTeX.com [frac{{{V_1}}}{{{V_2}}} = frac{{{S_{ocn}}}}{{pi {R^2}}} = frac{{frac{{{a^2}sqrt 3 }}{4}}}{{pi {{(frac{a}{{sqrt 3 }})}^2}}} = frac{{{a^2}sqrt 3 }}{{4pi cdot {{frac{a}{3}}^2}}} = frac{{3sqrt 3 }}{{4pi }}.]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-6bc755d0b75aa002afb503c0acf826ad_l3.png)
Отношение объема правильной четырехугольной призмы (то есть прямоугольного параллелепипеда, в основании которого лежит квадрат) к объему описанного около нее цилиндра равно
Отношение объема правильной шестиугольной призмы к объему описанного около нее цилиндра
(Как запомнить формулу для вычисления площади правильного шестиугольника, можно посмотреть здесь).
Отношение боковой поверхности вписанной призмы к объему описанного цилиндра:
Для правильной треугольной призмы это отношение равно
для правильной четырехугольной —
для правильной шестиугольной —


























![Rendered by QuickLaTeX.com [frac{{{V_1}}}{{{V_2}}} = frac{{{S_{ocn}}}}{{pi {R^2}}} = frac{{{a^2}}}{{pi {{(frac{a}{{sqrt 2 }})}^2}}} = frac{{{a^2}}}{{frac{{pi {a^2}}}{2}}} = frac{2}{pi },]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-b8c31e4a7a8ebe2037383d9d93644049_l3.png)
![Rendered by QuickLaTeX.com [frac{{{S_1}}}{{{S_2}}} = frac{{{P_{ocn}}}}{{2pi R}} = frac{{3a}}{{2pi cdot frac{a}{{sqrt 3 }}}} = frac{{3sqrt 3 }}{{2pi }},]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-860bebb36001e0a8ae5e4f0946650f4b_l3.png)
![Rendered by QuickLaTeX.com [frac{{{S_1}}}{{{S_2}}} = frac{{{P_{ocn}}}}{{2pi R}} = frac{{4a}}{{2pi cdot frac{a}{{sqrt 2 }}}} = frac{{2sqrt 2 }}{pi },]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-3f5184207976faf6598e54944ffb831e_l3.png)
