В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.

H – высота из прямого угла
a, b – катеты
с – гипотенуза
c1 , c2 – отрезки полученные от деления гипотенузы, высотой
α, β – углы при гипотенузе
Формула длины высоты через стороны, (H):

Формула длины высоты через гипотенузу и острые углы, (H):

Формула длины высоты через катет и угол, (H):

Формула длины высоты через составные отрезки гипотенузы , (H):

- Подробности
-
Опубликовано: 09 октября 2011
-
Обновлено: 13 августа 2021
Высота прямоугольного треугольника, проведенная к гипотенузе
Как и в любом треугольнике прямоугольный треугольник имеет три высоты. Две из них совпадают с катетами, а вот третья высота, проведенная к гипотенузе, постоянно будоражит наши умы.
Поэтому представляю вашему вниманию основные формулы для ее нахождения.
Начну с самой важной.
1. Высота, проведенная к гипотенузе равна корню квадратному из произведения проекций катетов на эту гипотенузу.
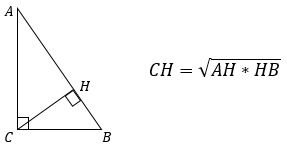
2. Высоту, проведенную к гипотенузе, можно найти, разделив удвоенную площадь прямоугольного треугольника на гипотенузу.
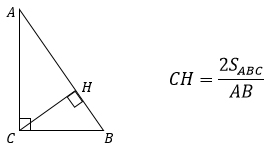
Такая формула получается из классический формулы нахождения площади треугольника: половина произведения основания на высоту, проведенную к этому основанию.
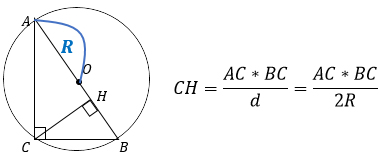
3. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на гипотенузу.
Эта формула получится из второй если заменить площадь на половину произведения катетов.
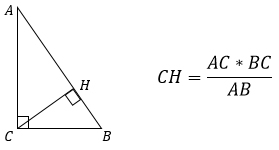
Т.к. АВ – гипотенуза, то ее можно выразить через катеты АС и ВС, используя теорему Пифагора. Тогда формула примет другой вид:
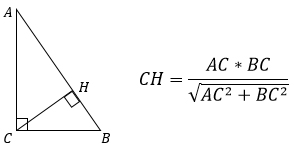
4. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на диаметр описанной вокруг треугольника окружности (или на удвоенный радиус).
Так получается потому, что центр описанной окружности лежит в середине гипотенузы, значит, гипотенуза равна 2R или d.
5. Высоту, проведенную к гипотенузе, можно найти, используя геометрические определения синуса, тангенса и котангенса.
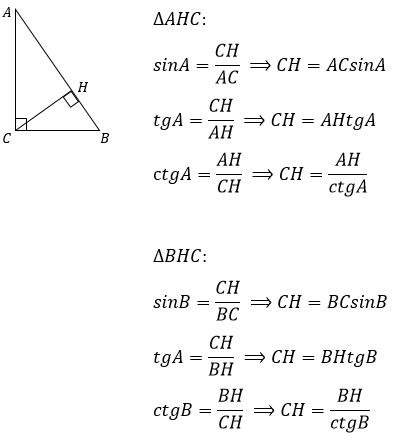
Надеюсь, что данная статья оказалась полезной!)
Готовься к экзамену вместе с нами! Заходи на нашу страницу в ВК.
Ответ:
Всё в разделе “Объяснение”.
Пошаговое объяснение:
- В прямоугольнике 4 стороны и все они являются высотами, так как высота – это перпендикуляр, проведённый из вершины прямоугольника к противоположной стороне этого прямоугольника.
- В прямоугольнике все углы прямые, поэтому все смежные стороны прямоугольника перпендикулярны друг к другу и являются перпендикулярами.
==============================================================
Существует множество способов нахождения высоты прямоугольника или стороны прямоугольника.
Рассмотрю 2 способа:
1) Можно найти, если известно:
Периметр прямоугольника P и одна из сторон прямоугольника a.
P = (a + b) * 2 (b – высота прямоугольника).
Тогда b = P : 2 – a.
2) Можно найти, если известно:
Площадь прямоугольника S и одна из сторон прямоугольника a.
S = ab (b – высота прямоугольника).
Тогда b = S : a.
Ответ:
Всё в разделе “Объяснение”.
Пошаговое объяснение:
- В прямоугольнике 4 стороны и все они являются высотами, так как высота – это перпендикуляр, проведённый из вершины прямоугольника к противоположной стороне этого прямоугольника.
- В прямоугольнике все углы прямые, поэтому все смежные стороны прямоугольника перпендикулярны друг к другу и являются перпендикулярами.
==============================================================
Существует множество способов нахождения высоты прямоугольника или стороны прямоугольника.
Рассмотрю 2 способа:
1) Можно найти, если известно:
Периметр прямоугольника P и одна из сторон прямоугольника a.
P = (a + b) * 2 (b – высота прямоугольника).
Тогда b = P : 2 – a.
2) Можно найти, если известно:
Площадь прямоугольника S и одна из сторон прямоугольника a.
S = ab (b – высота прямоугольника).
Тогда b = S : a.
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
-
Нахождение высоты треугольника
- Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
- Высота в прямоугольном треугольнике
- Высота в равностороннем треугольнике
- Примеры задач
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны
![]()
где S – площадь треугольника.
2. Через длины всех сторон
![]()
где p – это полупериметр треугольника, который рассчитывается так:
![]()
3. Через длину прилежащей стороны и синус угла
![]()
4. Через стороны и радиус описанной окружности
![]()

где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:


Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
![]()
2. Через стороны треугольника
![]()
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
![]()

Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
![]()
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
![]()
