Высота в прямоугольном треугольнике
Вспомним определение. Высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.
В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.
Один из типов экзаменационных задач в банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:

sin A
cos A
Высота проведена к гипотенузе AB. Она делит треугольник на два прямоугольных треугольника —
и
. Смотрим внимательно на рисунок и находим на нем равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.
Мы помним, что сумма двух острых углов прямоугольного треугольника равна . Значит,
, то есть угол
равен углу
. Аналогично, угол
равен углу
.
Иными словами, каждый из трех углов треугольника равен одному из углов треугольника
(и треугольника
). Треугольники
и
называются подобными. Давайте нарисуем их рядом друг с другом.

Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?
Возьмем треугольники и
. Стороны треугольника
длиннее, чем стороны треугольника
в
раз:
Мы доказали свойство высоты прямоугольного треугольника. Его можно сформулировать как теорему.
Теорема 1. Высота прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, делит треугольника на три подобных друг другу треугольника:
При решении задач нам пригодится равенство углов треугольников и
, а также пропорциональность их сторон. Обратите также внимание, что площадь треугольника
можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту. В геометрии это называется «метод площадей» и часто применяется в решении задач.
Задача 1.
В треугольнике ABC угол C равен CH — высота, BC = 3, cos A =
Найдите AH.

Решение:
Рассмотрим треугольник ABC. В нем известны косинус угла A и противолежащий катет BC. Зная синус угла A, мы могли бы найти гипотенузу AB. Так давайте найдем sin A:
sin + cos
= 1.
Эта формула – основное тригонометрическое тождество. Конечно, вы его знаете:
sin
sin
sin A (поскольку значение синуса острого угла положительно).
Тогда:
Рассмотрим прямоугольный треугольник ,
. Поскольку
Отсюда
Ответ:
Задача 2.
В треугольнике ABC угол C равен 90 AB = 13, tg A
. К гипотенузе проведена высота CH. Найдите AH.
Решение:
Это чуть более сложная задача. Ведь вам неизвестны катеты a и b.
Запишем теорему Пифагора: (1)
Нам известно также, что:
tg A (2)
Решая уравнения (1) и (2), найдем:
Запишем площадь треугольника AВС двумя способами:
и найдем длину .
Найти высоту, проведенную из вершины прямого угла, можно было и другим способом. Мы выбрали самый короткий путь — составили и решили систему уравнений, как в алгебре.
Теорема 2. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, равна произведению катетов, деленному на гипотенузу.

Доказательство:
Из прямоугольного треугольника ABC с прямым углом C и гипотенузой AB:
sin
Из прямоугольного треугольника AНС с прямым углом Н и гипотенузой AС:
sin
Мы разными способами вычислили синус одного и того же угла. Приравняем полученные выражения:
Найдем высоту:
Что и требовалось доказать.
Задача 3. Катеты прямоугольного треугольника равны 15 и 20.
Найдите высоту, проведенную к гипотенузе.
Решение:
Воспользуемся теоремой 2 о высоте прямоугольного треугольника:

Катеты BС и AС нам известны: BC = 15, AC = 20. Найдем гипотенузу AB с помощью теоремы Пифагора:
Найдем высоту, проведенную из вершины прямого угла:
Ответ: 12.
Теорема 3. В прямоугольном треугольнике квадрат высоты, проведенной из вершины прямого угла, равен произведению проекций катетов на гипотенузу.

Сейчас мы докажем эту полезную формулу.
Вспомним, что такое проекция точки на прямую. Например, из точки С опускаем СН – перпендикуляр к прямой AВ. Точка Н и будет проекцией точки С. Тогда AН – проекция катета AВ, а BН – проекция катета BС.
Обозначим:
Доказательство проведем двумя способами.
Первый способ доказательства:
Из прямоугольного треугольника BНС с прямым углом Н и гипотенузой BС:
tg
Из прямоугольного треугольника AНС с прямым углом Н и гипотенузой AС:
ctg
Заметим, что угол CBН – это угол CBA, а угол CAН – это угол BAC. Тогда:
tg
tg
Мы воспользовались тем, что тангенс и котангенс двух разных острых углов прямоугольного треугольника равны друг другу. Это следует из определения тангенса и котангенса.
Преобразуем получившееся выражение:
Что и требовалось доказать.
Второй способ доказательства:
Воспользуемся подобием треугольников, о которых говорится в теореме 1.
Рассмотрим пару прямоугольных треугольников AНC и BНC. Как было показано выше, эти треугольники подобны по двум углам, поэтому
Мы получили такое же соотношение, как и в первом способе доказательства.
Далее аналогично получим, что
Что и требовалось доказать.
Задача 4. На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH = 4, BH = 16. Найдите длину CH.
Решение:
Воспользуемся теоремой 3 о высоте прямоугольного треугольника:

Подставим данные задачи.
CH = 8.
Ответ: 8.
Разберем решения других задач ОГЭ и ЕГЭ по теме «Свойства высоты в прямоугольном треугольнике».
Задача 5. Катеты прямоугольного треугольника относятся как 3:4, а гипотенуза равна 50. Найти высоту, проведенную из вершины прямого угла и отрезки, на которые гипотенуза делится высотой.
Решение:
Рассмотрим прямоугольный треугольник ABС с гипотенузой AB. Проведем высоту CD=h.

Учитывая отношение катетов, обозначим их длины как: BC = 3x, AC = 4x.
Тогда по теореме Пифагора получим:
По условию гипотенуза AB = 50. Следовательно, х = 10, BC = 30, AC = 40.
Далее можно действовать разными способами. Например, так.
где по определению косинуса:
cos A cos B
Ответ:
Задача 6. В прямоугольном треугольнике ABC высота CD делит гипотенузу на отрезки AD = 3 см и BD = 2 см. Найти катеты треугольника.
Решение:

Найдем квадрат длины высоты с помощью теоремы 3:
Из прямоугольного треугольника ADC по теореме Пифагора найдем
см.
Из прямоугольного треугольника BDC по теореме Пифагора найдем
см.
Ответ: см и
см.
Задача 7. Точка D является основанием высоты, проведенной из вершины прямого угла C треугольника ABC к гипотенузе AB. Найдите AC, если AD=8, AB=32.
Указание:
Найдите отрезок BD = AB – AD, после чего задача сводится к предыдущей.
Длину высоты прямоугольного треугольника можно также найти, если известны гипотенуза и один из острых углов треугольника.
h = c sincos
= c sin
cos
Докажем эту формулу.

Рассмотрим прямоугольный треугольник ACD:
В то же время из треугольника AВC:
Таким образом, h = CD = AC cos = AB sin
cos
= c sin
cos
Аналогично, из треугольника BCD получим: h = CD = BC cos = AB sin
cos
= c sin
cos
Задача 8. В прямоугольном треугольнике гипотенуза равна 10, а один из острых углов 15 градусов. Найти высоту, проведенную из вершины прямого угла.
Решение:
Воспользуемся доказанной выше формулой:
h = c sincos
= 10 sin
cos
= 5sin
= 2,5.
Ответ: 2,5.
Задача 9. Высота прямоугольного треугольника делит его гипотенузу на отрезки 6 см и 4 см. Найдите площадь этого треугольника.
Решение:

Гипотенуза прямоугольного треугольника равна сумме данных отрезков:
см.
Найдем высоту, проведенную из вершины прямого угла к гипотенузе: см.
Площадь треугольника:
см
Ответ: см
Если вам понравился наш материал – записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Высота в прямоугольном треугольнике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
-
Нахождение высоты треугольника
- Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
- Высота в прямоугольном треугольнике
-
Высота в равностороннем треугольнике
- Примеры задач
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны
![]()
где S – площадь треугольника.
2. Через длины всех сторон
![]()
где p – это полупериметр треугольника, который рассчитывается так:
![]()
3. Через длину прилежащей стороны и синус угла
![]()
4. Через стороны и радиус описанной окружности
![]()

где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:


Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
![]()
2. Через стороны треугольника
![]()
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
![]()

Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
![]()
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
![]()
Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.
2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности


где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:


Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:


Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Способы нахождения высоты треугольника: теорема и формула
Определение высоты треугольника
Геометрия, являющаяся разделом математики, изучает структуры в пространстве и на плоскости. Одним из типов таких фигур являются геометрические фигуры. К ним можно отнести квадрат, прямоугольник, круг, пятиугольник, треугольник и другие. Из них можно делать более сложные фигуры или оставлять в первоначальном виде.
Треугольником является фигура, относящаяся к классу простых фигур, которая образована тремя точками, находящимися не на одной прямой, и соединенными между собой тремя отрезками.
Треугольники могут быть:
- разными по величине углов: прямоугольными, тупоугольными и остроугольными;
- разными по числу равных сторон: равносторонними, равнобедренными и разносторонними.
Помимо трех сторон, важными элементами треугольников являются медианы, высоты и биссектрисы.
Высотой треугольника является перпендикуляр, опущенный из угла треугольника вниз, на противоположную сторону.
В геометрии высота треугольника обозначается буквой h.
В зависимости от типа треугольника высота может:
- падать на противоположную сторону — у остроугольного треугольника;
- находиться вне треугольника — у тупоугольного треугольника;
- совпадать с одной из сторон — у прямоугольного треугольника.
Чтобы сделать высоту графически явной и понятной на рисунке, ее нередко выделяют красной линией.
Для того чтобы определить графическое начертание высоты треугольника, необходимо:
- Найти вершину фигуры.
- Опустить вниз перпендикулярную линию к противоположной стороне.
- Продлить противоположную сторону до пересечения с высотой, если требуется.
Любой треугольник имеет 3 высоты — по числу углов. Их пересечение находится в точке ортоцентра, которая, в зависимости от типа треугольника, может находиться внутри треугольника, снаружи на пересечении продолжений высот или совпадать с вершиной прямого угла.
Все три высоты треугольника обратно пропорциональны сторонам, к которым опущены. Доказательством будет соотношение:
A × H A ÷ B × H B ÷ C × H C = 1 B C ÷ 1 A C ÷ 1 A B
Выглядеть графически это будет так:
Существует множество способов нахождения высоты треугольника в зависимости от имеющихся данных.
Через площадь и длину стороны, к которой опущена высота:
где S — уже известная площадь треугольника,
Через длины всех сторон:
h = 2 p p × a p × b p × c a
где a, b и c — стороны треугольника,
p — его полупериметр.
Данная формула подходит только для нахождения высоты разностороннего треугольника.
Через длину прилежащей стороны и синус угла:
s i n a — синус угла прилежащей стороны.
Данная формула подходит только для нахождения высоты разностороннего треугольника.
Через стороны и радиус описанной окружности.
Решать задачи с треугольником и описанной окружностью для нахождения высоты можно следующим образом:
где b, c — стороны разностороннего треугольника, к которым не опущена высота,
R — радиус описанной окружности.
Данная формула подходит только для нахождения высоты разностороннего треугольника.
Через длины отрезков, образованных на гипотенузе при проведении к ней высоты треугольника:
где C 1 и С 2 — длины отрезков, образованных на гипотенузе, проведенной к ней высотой.
Данная формула подходит только для нахождения высоты прямоугольного треугольника.
Нахождение высоты равнобедренного треугольника через основание и боковые стороны
Равнобедренным треугольником называют треугольник, имеющий одинаковые по длине катеты, которые образуют равные углы с основанием. В таком треугольнике высота будет опускаться ровно в середину основания, образуя с ним прямой угол.
Помимо высоты, проведенная линия будет являться также осью симметрии, биссектрисой вершинного угла и медианой.
Формула для нахождения высоты в этом случае:
где a — основание,
b — равные боковые стороны.
Свойства высоты в равностороннем треугольнике
Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.
Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.
Высоту в таком треугольнике можно найти с помощью следующей формулы:
где а — сторона равностороннего треугольника.
Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:
а — сторона правильного равностороннего треугольника.
Нахождение высоты прямоугольного треугольника через его катеты
Прямоугольным считается треугольник, у которого один из углов является прямым, то есть равным 90°. Высота, опущенная из такого угла, падает на гипотенузу треугольника и делит его на два прямоугольных треугольника, которые пропорциональны по отношению к большому треугольнику и друг к другу.
Важно отметить, что две другие высоты будут совпадать с катетами треугольника.
Найти высоту в прямоугольном треугольнике, можно через два его катета (a и b) и гипотенузу (c).
Причем гипотенуза также легко находится через катеты по теореме Пифагора:
Расчет высоты идет следующим образом:
где a, b и c — вышеупомянутые стороны треугольника.
Теорема Пифагора

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Гипотенуза — сторона, лежащая напротив прямого угла.
Катет — одна из двух сторон, образующих прямой угол.
Формула Теоремы Пифагора выглядит так:
где a, b — катеты, с — гипотенуза.
Из этой формулы можно вывести следующее:
- a = √c 2 − b 2
- b = √c 2 − a 2
- c = √a 2 + b 2
Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:
- если c 2 2 + b 2 , значит угол, противолежащий стороне c, является острым.
- если c 2 = a 2 + b 2 , значит угол, противолежащий стороне c, является прямым.
- если c 2 > a 2 +b 2 , значит угол, противолежащий стороне c, является тупым.
Записывайтесь на курсы обучения математике для школьников с 1 по 11 классы!
Теорема Пифагора: доказательство
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Дано: ∆ABC, в котором ∠C = 90º.
Доказать: a 2 + b 2 = c 2 .
Пошаговое доказательство:
- Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
- Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:
- Также прямоугольная фигура ∆CBH подобна ∆ABC:
- Введем новые обозначения: BC = a, AC = b, AB = c.
- Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.
- Значит a 2 = c * HB, b 2 = c * AH.
- Сложим полученные равенства:
a 2 + b 2 = c * HB + c * AH
a 2 + b 2 = c * (HB + AH)
a 2 + b 2 = c * AB
Обратная теорема Пифагора: доказательство
Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.
Дано: ∆ABC
Доказать: ∠C = 90º
Пошаговое доказательство:
- Построим прямой угол с вершиной в точке C₁.
- Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.
- Проведём отрезок A₁B₁.
- Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.
- В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
- Таким образом получится:
- Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:
- C₁A₁ = CA и C₁B₁ = CB по результату построения,
- A₁B₁ = AB по доказанному результату.
- Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
- Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.
Обратная теорема доказана.
Решение задач
Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?
Как решаем:
Пусть катеты a = 6 и b = 8.
По теореме Пифагора c 2 = a 2 + b 2 .
Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.
Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?
- Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:
Ответ: треугольник не является прямоугольным.
[spoiler title=”источники:”]
http://wika.tutoronline.ru/geometriya/class/7/sposoby-nahozhdeniya-vysoty-treugolnika-teorema-i-formula
http://skysmart.ru/articles/mathematic/teorema-pifagora-formula
[/spoiler]
Найти высоту прямоугольного треугольника, используя теорему Пифагора
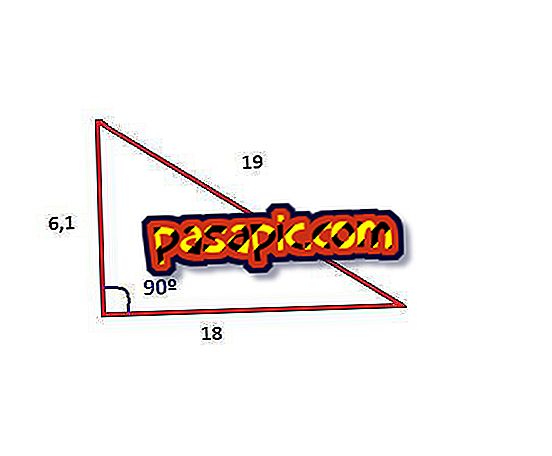
Высоту треугольника можно найти по-разному, в зависимости от типа треугольника и информации, которую вы имеете или измеряете. Прямоугольные треугольники, которые включают угол 90 градусов, легче всего измерить, используя теорему Пифагора (если известны длины двух сторон) или формулу области (если область и основание известны). Равносторонние треугольники, в которых все стороны имеют одинаковую длину, и равнобедренные треугольники, в которых три их стороны имеют одинаковую длину, можно разрезать пополам, создав два прямоугольных треугольника. Косые треугольники, те, которые не имеют внутренний угол, равный 90 градусам, являются более сложными и требуют тригонометрии, чтобы найти их высоту. Далее мы вычислим высоту прямоугольного треугольника, используя теорему Пифагора.
Вам понадобится:
- Научный калькулятор
- транспортир
- правило
Шаги, чтобы следовать:
1
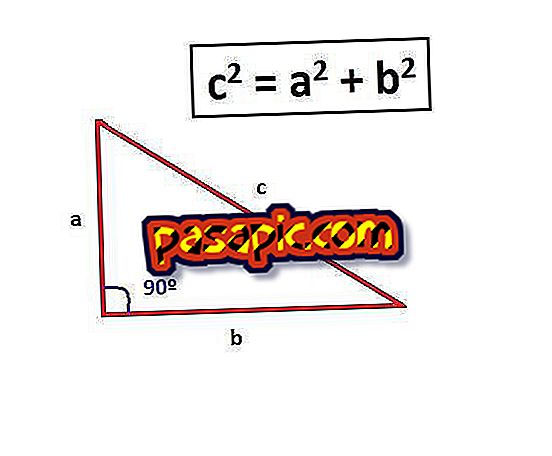
Первое, что вы должны сделать, чтобы вычислить высоту треугольника, это написать теорему Пифагора, c ^ 2 = a ^ 2 + b ^ 2, где c – гипотенуза (диагональ).
2
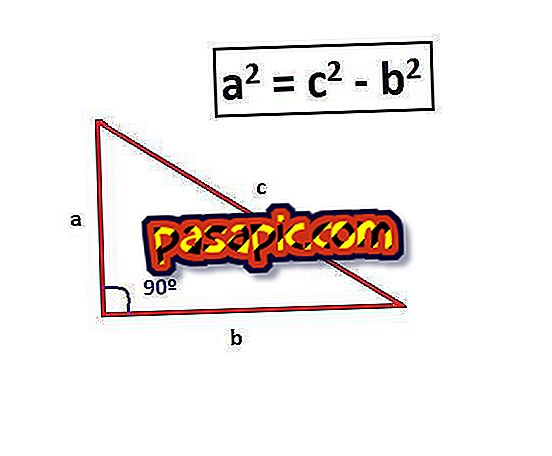
Реорганизовать теорему, чтобы решить a ^ 2, поэтому a ^ 2 = c ^ 2 – b ^ 2. Мы хотим найти значение «a», потому что, как мы видим на изображении, это высота треугольника.
3
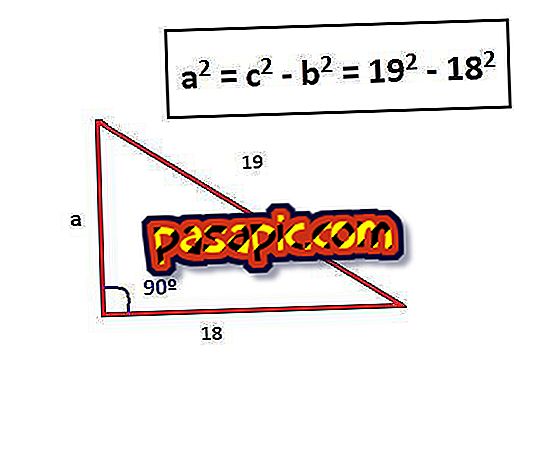
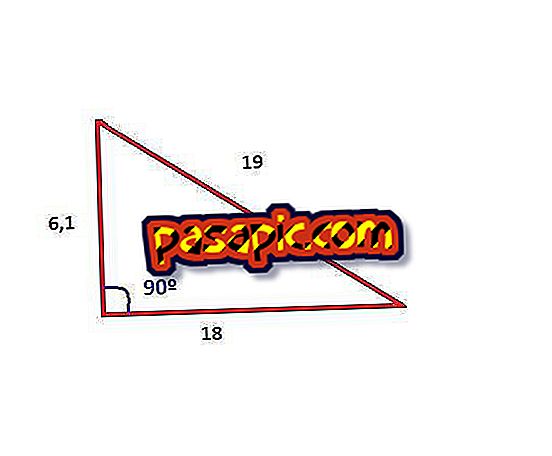
Соедините две стороны известных значений cyb, которые в нашем случае мы дадим значение:
- с = 19
- б = 18
Поэтому остается, что [a ^ 2 = 19 ^ 2 – 18 ^ 2]
4
Далее мы решаем уравнение, и мы должны:
^ 2 = 361 – 324 = 37
5
Чтобы закончить и найти реальное значение высоты треугольника, вам нужно взять квадратный корень с обеих сторон, чтобы найти высоту a ^ 2. [a = 6.1]
 чаевые
чаевые
- Основание может быть любой стороной треугольника.
- Метод тригонометрии (с использованием синуса) можно применять и к прямоугольным треугольникам.
- Три угла треугольника должны составлять до 180 градусов.
Высота прямоугольного треугольника, проведенная к гипотенузе
Как и в любом треугольнике прямоугольный треугольник имеет три высоты. Две из них совпадают с катетами, а вот третья высота, проведенная к гипотенузе, постоянно будоражит наши умы.
Поэтому представляю вашему вниманию основные формулы для ее нахождения.
Начну с самой важной.
1. Высота, проведенная к гипотенузе равна корню квадратному из произведения проекций катетов на эту гипотенузу.
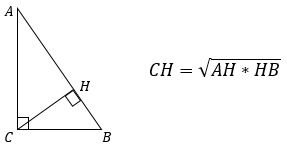
2. Высоту, проведенную к гипотенузе, можно найти, разделив удвоенную площадь прямоугольного треугольника на гипотенузу.
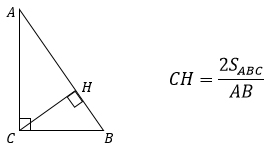
Такая формула получается из классический формулы нахождения площади треугольника: половина произведения основания на высоту, проведенную к этому основанию.
3. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на гипотенузу.
Эта формула получится из второй если заменить площадь на половину произведения катетов.
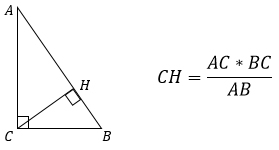
Т.к. АВ – гипотенуза, то ее можно выразить через катеты АС и ВС, используя теорему Пифагора. Тогда формула примет другой вид:
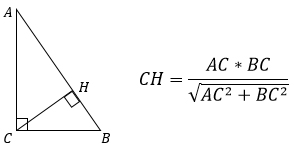
4. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на диаметр описанной вокруг треугольника окружности (или на удвоенный радиус).
Так получается потому, что центр описанной окружности лежит в середине гипотенузы, значит, гипотенуза равна 2R или d.
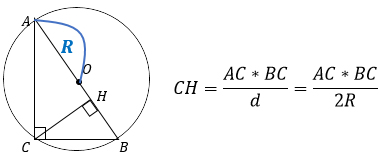
5. Высоту, проведенную к гипотенузе, можно найти, используя геометрические определения синуса, тангенса и котангенса.
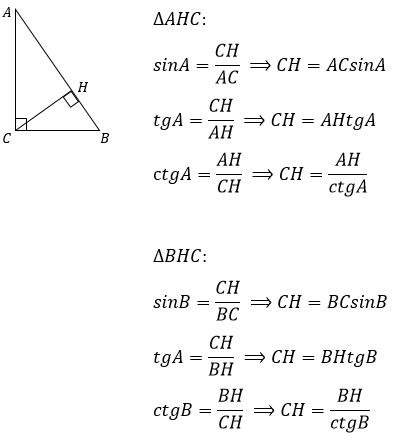
Надеюсь, что данная статья оказалась полезной!)
Готовься к экзамену вместе с нами! Заходи на нашу страницу в ВК.
