Высота, проведенная в любом треугольнике, делит его на два прямоугольных треугольника, становясь смежным катетом. Сторона, на которую опущена высота, оказывается также разделенной на две пропорциональных части. Зная все три стороны, можно собрать их по теореме Пифагора, и приравняв высоту в качестве катета в двух вышеуказанных треугольниках, получить ее формулу для любого произвольного треугольника:
С другой стороны, можно использовать сторону, прилежащую к высоте и угол α, чтобы вычислить высоту треугольника.
Известная его сторона будет гипотенузой в прямоугольном треугольнике, а сама высота – катетом, противолежащим углу α. Два этих измерения связывает синус угла, поэтому высота равна его произведению на сторону a:
h=a sinα
Высота в прямоугольном треугольнике, опущенная из прямого угла (остальные две совпадают с катетами), получает особые свойства. Так как все три получившихся прямоугольных треугольника подобны друг другу, их стороны составляют пропорцию, которая раскладывается как квадрат высоты, равный произведению проекцию катетов на гипотенузу, или проще говоря, частей гипотенузы, на которые ее делит высота.
Из этого следует, что высота равна квадратному корню из данного произведения, а это есть не что иное как среднее пропорциональное приведенного выражения.
В равностороннем треугольнике, высота делит угол, из которого она исходит, на два одинаковых угла по 30°. Высота, оказываясь катетом, прилежащим к этому углу, внутри прямоугольного треугольника, подчиняется отношению косинуса угла α, а так как 
Здесь рассмотрены все возможные способы нахождения высоты треугольников разных типов. Высота
треугольника – отрезок, проведенный из вершины треугольника перпендикулярно к противоположной
стороне. В задачах нахождение высоты часто является промежуточным звеном для поиска других значений.
Она и является катетом в треугольнике, который сама же образует, и участвует во многих формулах,
например, для нахождения площади.
- Высота разностороннего треугольника через площадь и длину
стороны - Высота разностороннего треугольника через длины всех
сторон - Высота разностороннего треугольника через длину прилежащей
стороны и синус угла - Высота разностороннего треугольника через стороны и радиус
описанной окружности - Высота равнобедренного треугольника через основание и
боковые стороны - Высота прямоугольного треугольника через длины отрезков,
образованных на гипотенузе - Высота прямоугольного треугольника через все стороны
треугольника - Высота равностороннего треугольника через сторону
треугольника
Через площадь и длину стороны разностороннего треугольника
Через площадь и длину высота находится по формуле:
h = 2S / a
где S – площадь треугольника, а – сторона треугольника.
Цифр после
запятой:
Результат в:
Согласно этой формуле высота равна удвоенной площади, деленной на длину стороны, к которой она
проведена.
Пример. Найдите высоту разностороннего треугольника, проведенную к стороне а,
площадь которого равна 27 см, а длина стороны а составляет одну треть от площади. Решение: Найдем
сторону а. Так как известно, что она составляет треть от площади, а = 27 / 3 = 9 см.
Теперь воспользуемся формулой для нахождения высоты: h = 2S / a. Подставим
известные значения. h = 2 * 27 / 9 = 6 см. Ответ: 6 см
Через длины всех сторон разностороннего треугольника
Через длины всех сторон высота разностороннего треугольника ищется по формуле:
h = (2 √(p (p-a)(p-b)(p-c))) / 2
p = (a + b + c) / 2
где h – высота, а, b, c – стороны треугольника, p – полупериметр треугольника.
Цифр после
запятой:
Результат в:
Полупериметр треугольника можно найти либо в два этапа через периметр, либо сразу по формуле. Этим
способом удобно пользоваться, когда треугольник разносторонний.
Пример. Периметр разностороннего треугольника равен 18 см. Длины сторон 6 см и 8 см. Найдите
высоту, проведенную к стороне а. Решение: P = a + b + c, значит с = P – a – b , то есть c = 18 – 8 – 6 = 4 см. Для
нахождения h будем использовать формулу h = (2 √(p (p-a)(p-b)(p-c))) / 2.
Сначала найдем полупериметр (p): p = p / 2 = 18 / 2 = 9 см. Подставим,
найденные значения в формулу высоты: h = (2 √(9 (9 — 6)(9 — 8)(9 — 4))) / 2 = √135 / 3 = 2,12 см
Через длину прилежащей стороны и синус угла разностороннего треугольника
Через длину прилежащей стороны и синус угла высота ищется по следующей формуле:
h = a * sin α
где а – длина стороны, sin α – синус прилежащей стороны.
Цифр после
запятой:
Результат в:
Пример. В разностороннем треугольнике высота проведена к стороне AB. Угол ACH равен
30˚, а длина стороны AB 12 см. Найдите длину высоты CH в треугольнике ABC. По теореме о сумме углов
в треугольнике найдем угол САН. ∠САН = 180 – (∠АСН + ∠АНС). ∠САН = 180 – 90 – 30 = 60˚ sin 60º = 1/2. СН = AB * sin ∠САН, СН = 12 * 1/2 = 6 см. Ответ:
6 см
Через стороны и радиус описанной окружности разностороннего треугольника
Через стороны и радиус описанной окружности высоту можно найти по следующей формуле:
h = bc / 2R
где r – радиус описанной около треугольника окружности, b,c – стороны треугольника
Цифр после
запятой:
Результат в:
Пример. Вокруг разностороннего треугольника описана окружность с радиусом 3 см. Из
вершины между сторонами b и с проведена высота. Стороны b и с соответственно равны 5 см и 6 см.
Найдите высоту. Решение: Найдем высоту, используя формулу h = 5 * 6 / 2 * 3 = 30 / 6 = 5 см. Ответ:
5 см.
Через длины отрезков прямоугольного треугольника, образованных на гипотенузе
Через длины отрезков образованных на гипотенузе высоту можно найти по следующей формуле:
h = √(C1 * C2)
где: C1, C2 — отрезки, образованные проведением высоты к гипотенузе.
Цифр после
запятой:
Результат в:
Пример. В прямоугольном треугольнике катеты равны 4 см и 3 см. Угол BAH равен 30˚.
Найдите высоту. По теореме Пифагора найдём сторону BC, которая является гипотенузой в треугольнике
ABC. BC² = AB² = AC², BC² = 4² + 3² = 16+9 = 25 см², BC = √25 = 5 см. Угол
АНВ равен 90˚, так как АН является высотой, то есть, проведена перпендикулярно к стороне ВС.
Следовательно, треугольник АНВ – прямоугольный. Сторона ВН лежит напротив угла 30˚ в прямоугольном
треугольнике, значит, ее длина равна половине длины гипотенузы. Найдем ВН. BH = 1/2 AB. BH = 1/2 × 4 = 2 см. BC = BH + HC,
значит, HC = BC – BH, HC = 5 – 2 = 3 см. По формуле найдем высоту
(АН). АН = √(2 * 3) = √6 = 2,4 см. Ответ: 2,4 см.
Через основание и боковые стороны равнобедренного треугольника
Через основание и боковые стороны высота равнобедренного треугольника находится по формуле:
h = √(b² — a²/4)
где а – основание треугольника, b – боковая сторона. Для равнобедренного треугольника.
Цифр после
запятой:
Результат в:
Пример. В равнобедренном треугольнике АВС боковая сторона равна 8 см. Из вершины В к
основанию АС проведена высота ВН. Отрезок АН равен 5 см. Найдите высоту. Решение: Так как по условию
треугольник АВС равнобедренный по условию, то АВ = ВС = 8 см высота ВН,
является и медианой, и биссектрисой. Значит, АН = НС, а АС = НС + АН, АС = 5 + 5 = 10 см. По
формуле найдем высоту ВН = √(АВ² — АС² / 4). ВН = √(8² — 10² / 4) = √(64 — 100 / 4) = √39 = 6 см.
Ответ: 6 см.
Высота прямоугольного треугольника через все стороны треугольника
Если известны все стороны прямоугольного треугольника, то можно найти его высоту по следующей
формуле:
h = ab / c
где a,b,c – стороны треугольника.
Цифр после
запятой:
Результат в:
Пример. В прямоугольном треугольнике угол между катетом и гипотенузой равен 45˚.
Длина стороны АС равна 6 см. Найти высоту АН. Решение: По теореме о сумме углов в треугольнике
найдем угол АСВ. ∠АСВ = 180˚ – (45˚ + 90˚) = 45˚. Так как АСВ = АСВ, то
треугольник АВС равнобедренный с основанием ВС. Таким образом, АС = АВ = 6 см. По теореме Пифагора найдем гипотенузу ВС. BC² = AB² + AC². BC² = 6² + 6² = 36 +36 = 72 см². ВС = √72 = 6√2 см. Найдем
высоту по формуле AH = AB * AC / BC. АН = 6 * 6 / 6√2= см. Домножим
полученное значение на √2: (6 * √2) / √2 * √2 = 6√2 / 2 = 3√2 см. Ответ:
3√2 см
Через сторону равностороннего треугольника
Высота равностороннего треугольника через сторону треугольника ищется по следующей формуле:
h = a√3 / 2
где a – сторона треугольника.
Цифр после
запятой:
Результат в:
Пример: Найдите высоту в равностороннем треугольнике, если известно, что его сторона
равна 4√3 см. Решение: Для нахождения высоты воспользуемся формулой h = a√3 / 2 = √3 * 4 √3 / 2 = 4 * 3 / 2 = 6 см. Ответ:
6 см
В зависимости от типа треугольника высота может располагаться по-разному:
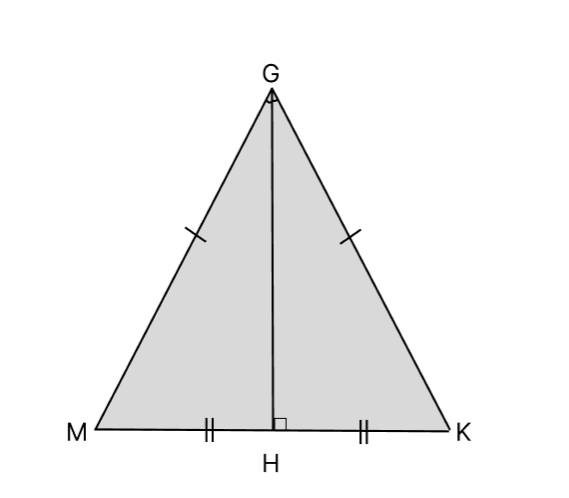
- Например, в треугольнике KGM высота GH, проведённая из вершины G к стороне находится внутри
треугольника, так как треугольник является остроугольным. Кроме того, треугольник в данном
примере равнобедренный, значит, она же является биссектрисой и медианой. Знание этого пригодится
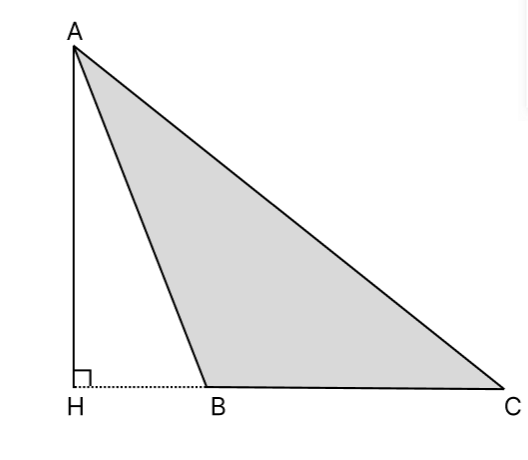
при решении задач, например таким образом можно будет найти основание. - В тупоугольном треугольнике высота будет выходить за его пределы и для того чтобы её провести
понадобится сначала продлить сторону. Например, на рисунке сторона ВС продлена до НС. - В случае, когда треугольник имеет прямой угол – высота совпадёт с одним из катетов, либо будет
внутри треугольника (как в первом рассмотренном варианте) и проведена к гипотенузе.
Please provide 2 values below to calculate the other values of a right triangle. If radians are selected as the angle unit, it can take values such as pi/3, pi/4, etc.
Right triangle
A right triangle is a type of triangle that has one angle that measures 90°. Right triangles, and the relationships between their sides and angles, are the basis of trigonometry.
In a right triangle, the side that is opposite of the 90° angle is the longest side of the triangle, and is called the hypotenuse. The sides of a right triangle are commonly referred to with the variables a, b, and c, where c is the hypotenuse and a and b are the lengths of the shorter sides. Their angles are also typically referred to using the capitalized letter corresponding to the side length: angle A for side a, angle B for side b, and angle C (for a right triangle this will be 90°) for side c, as shown below. In this calculator, the Greek symbols α (alpha) and β (beta) are used for the unknown angle measures. h refers to the altitude of the triangle, which is the length from the vertex of the right angle of the triangle to the hypotenuse of the triangle. The altitude divides the original triangle into two smaller, similar triangles that are also similar to the original triangle.
If all three sides of a right triangle have lengths that are integers, it is known as a Pythagorean triangle. In a triangle of this type, the lengths of the three sides are collectively known as a Pythagorean triple. Examples include: 3, 4, 5; 5, 12, 13; 8, 15, 17, etc.
Area and perimeter of a right triangle are calculated in the same way as any other triangle. The perimeter is the sum of the three sides of the triangle and the area can be determined using the following equation:
Special Right Triangles
30°-60°-90° triangle:
The 30°-60°-90° refers to the angle measurements in degrees of this type of special right triangle. In this type of right triangle, the sides corresponding to the angles 30°-60°-90° follow a ratio of 1:√3:2. Thus, in this type of triangle, if the length of one side and the side’s corresponding angle is known, the length of the other sides can be determined using the above ratio. For example, given that the side corresponding to the 60° angle is 5, let a be the length of the side corresponding to the 30° angle, b be the length of the 60° side, and c be the length of the 90° side.:
Angles: 30°: 60°: 90°
Ratio of sides: 1:√3:2
Side lengths: a:5:c
Then using the known ratios of the sides of this special type of triangle:
As can be seen from the above, knowing just one side of a 30°-60°-90° triangle enables you to determine the length of any of the other sides relatively easily. This type of triangle can be used to evaluate trigonometric functions for multiples of π/6.
45°-45°-90° triangle:
The 45°-45°-90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°-45°-90°, follow a ratio of 1:1:√2. Like the 30°-60°-90° triangle, knowing one side length allows you to determine the lengths of the other sides of a 45°-45°-90° triangle.
Angles: 45°: 45°: 90°
Ratio of sides: 1:1:√2
Side lengths: a:a:c
Given c= 5:
45°-45°-90° triangles can be used to evaluate trigonometric functions for multiples of π/4.
Высота прямоугольного треугольника Калькулятор
| Search | ||
| Дом | математика ↺ | |
| математика | Геометрия ↺ | |
| Геометрия | 2D геометрия ↺ | |
| 2D геометрия | Треугольник ↺ | |
| Треугольник | Прямоугольный треугольник ↺ | |
| Прямоугольный треугольник | Высота прямоугольного треугольника ↺ |
|
✖Высота прямоугольного треугольника – это длина перпендикулярной стороны прямоугольного треугольника, примыкающей к основанию.ⓘ Высота прямоугольного треугольника [h] |
+10% -10% |
||
|
✖Основание прямоугольного треугольника — это длина стороны основания прямоугольного треугольника, примыкающей к перпендикулярной стороне.ⓘ Основание прямоугольного треугольника [B] |
+10% -10% |
|
✖Высота прямоугольного треугольника — это длина вертикального расстояния от гипотенузы до вершины, образованной соединением основания и высоты прямоугольного треугольника.ⓘ Высота прямоугольного треугольника [h’] |
⎘ копия |
Высота прямоугольного треугольника Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Высота прямоугольного треугольника: 8 метр –> 8 метр Конверсия не требуется
Основание прямоугольного треугольника: 15 метр –> 15 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
7.05882352941176 метр –> Конверсия не требуется
2 Высота прямоугольного треугольника Калькуляторы
9 Важные формулы прямоугольного треугольника Калькуляторы
Высота прямоугольного треугольника формула
Высота прямоугольного треугольника = (Высота прямоугольного треугольника*Основание прямоугольного треугольника)/sqrt(Высота прямоугольного треугольника^2+Основание прямоугольного треугольника^2)
h’ = (h*B)/sqrt(h^2+B^2)
Что такое прямоугольный треугольник?
Прямоугольный треугольник или прямоугольный треугольник, или, более формально, ортогональный треугольник — это треугольник, в котором один угол является прямым. Соотношение между сторонами и углами прямоугольного треугольника является основой тригонометрии. Сторона, противолежащая прямому углу, называется гипотенузой.
Информация по назначению калькулятора
Треугольник – это одна из основных геометрических фигур: многоугольник с тремя углами (или вершинами) и тремя сторонами (или ребрами), которые являются прямыми отрезками.
В евклидовой геометрии любые три неколлинеарные точки определяют треугольник и единственную плоскость, то есть двумерное декартово пространство.
Сумма длин любых двух сторон треугольника всегда превышает длину третьей стороны. Это и есть неравенство треугольника.
Треугольники могут быть классифицированы в соответствии с относительной длиной их сторон:
⇒ В равностороннем треугольнике все стороны имеют одинаковую длину. Равносторонний треугольник также является равноугольным многоугольником, т.е. все его внутренние углы равны, а именно 60° – это правильный многоугольник.
⇒ В равнобедренном треугольнике две стороны имеют одинаковую длину. Равнобедренный треугольник также имеет два совпадающих угла (а именно, углы, противоположные совпадающим сторонам). Равносторонний треугольник – это равнобедренный треугольник, но не все равнобедренные треугольники являются равносторонними треугольниками.
⇒ В скалярном треугольнике все стороны имеют разную длину. Внутренние углы в скалярном треугольнике все разные.
Треугольники также могут быть классифицированы в соответствии с их внутренними углами:
⇒ Прямоугольный треугольник имеет один внутренний угол 90° (прямой угол). Сторона, противоположная прямому углу, является гипотенузой; это самая длинная сторона в прямоугольном треугольнике. Две другие стороны – катеты треугольника.
⇒ Тупой треугольник имеет один внутренний угол, больший 90° (тупой угол).
⇒ Острый треугольник имеет внутренние углы, которые все меньше 90° (три острых угла). Равносторонний треугольник – это острый треугольник, но не все острые треугольники являются равносторонними треугольниками.
⇒ Наклонный треугольник имеет только углы, которые меньше или больше 90°. Следовательно, это любой треугольник, который не является прямоугольным треугольником.
Онлайн калькулятор поможет найти параметры треугольника, такие как:
- Длины сторон
- Углы
- Высота
- Периметр
- Площадь
- Медианы
- Биссектрисы
- Радиус Вписанной и Описанной окружностей
- Диаметр Вписанной и Описанной окружностей
- Длина Вписанной и Описанной окружностей
- Площадь Вписанной и Описанной окружностей
– равны в равностороннем треугольнике
– также равны в равностороннем треугольнике
– это прямая линия, проходящая через вершину и перпендикулярная противоположной стороне (т. е. образующая прямой угол с ней)
– равен сумме всех 3х сторон (P=AB+BC+AC)
– равна половине произведения высоты и стороны к которой построена высота (S=1/2 * H * AC)