В данной публикации мы рассмотрим различные формулы, с помощью которых можно вычислить высоту прямоугольной трапеции.
Напомним, в прямоугольной трапеции одна из боковых сторон перпендикулярна ее основаниями, и потому одновременно является высотой фигуры.
-
Нахождение высоты прямоугольной трапеции
- Через длины сторон
-
Через основания и прилежащий угол
- Через боковую сторону и прилежащий угол
- Через диагонали и угол между ними
- Через площадь и основания
Нахождение высоты прямоугольной трапеции
Через длины сторон
Зная длины обоих оснований и большей боковой стороны прямоугольной трапеции, можно найти ее высоту (или меньшую боковую сторону):
Данная формула следует из теоремы Пифагора. В данном случае высота h – это неизвестный катет прямоугольного треугольника, гипотенуза которого равняется d, а известный катет – разности оснований, т.е. (a-b).
Через основания и прилежащий угол
Если даны длины оснований и любой из прилежащих к ним острых углов, то вычислить высоту прямоугольной трапеции можно по формуле:
Через боковую сторону и прилежащий угол
Если известна длина боковой стороны прямоугольной трапеции и прилежащий к ней угол (любой), найти высоту фигуры удастся таким образом:
Примечание: с помощью этой формулы можно, в т.ч., доказать, что меньшая боковая сторона – это и есть высота трапеции:
Через диагонали и угол между ними
При условии, что известны длины оснований прямоугольной трапеции, диагонали и угол между ними, рассчитать высоту фигуры можно так:
Если вместо суммы оснований известна длина средней линии, то формула примет вид:
m – средняя линия, которая равна половине суммы оснований, т.е.m = (a+b)/2.
Через площадь и основания
Если известна площадь прямоугольной трапеции и длина ее оснований (или средней линии), найти высоту можно таким образом:
Определения
Трапеция — это такой четырехугольник, у которого две стороны параллельны (они являются основаниями трапеции, указанные на рисунках a и b), а две другие — нет.
Высота трапеции — это такой отрезок h, который проведен перпендикулярно основаниям.
Нахождение высоты по площади и основаниям
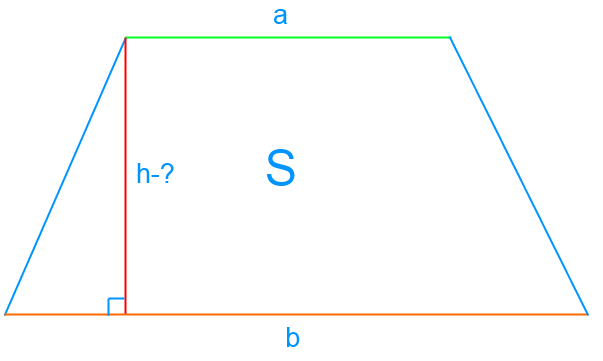
Чтобы вычислить площадь S трапеции мы используем формулу:
[S=frac{((a+b) times h)}{2}]
Здесь h — высота трапеции, а сегменты a и b являются ее основаниями.
Можем найти h:
[h=frac{2 times S}{(a+b)}]
Пример 1
Площадь трапеции S составляет 50 см2, длина ее основания a = 4 см, длина второго основания b равна 6 см, то для нахождения высоты h мы используем формулу:
[h=frac{2 times 50}{(4+6)}=10 mathrm{~cm}]
Ответ: 10 см.
Нахождение высоты, зная площадь и среднюю линию
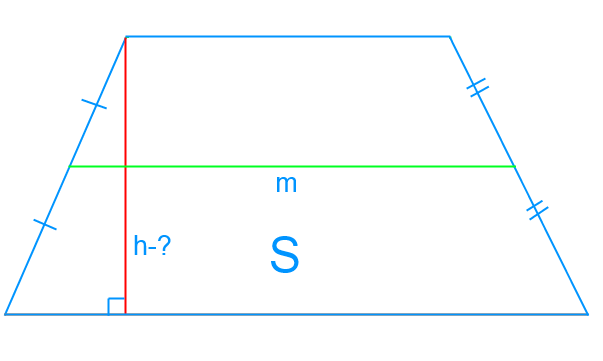
Мы используем формулу, с помощью которой можно рассчитать площадь трапеции:
S = m × h,
Здесь h — это высота трапеции, m — ее средняя линия.
Можем найти h:
[h=frac{S}{m}], будет ответом.
Пример 2
Средняя линия трапеции, обозначенная буквой m, равна 20 см, а площадь S, которая составляет 200 см2. Давайте найдем значение высоты трапеции h.
[h=frac{200}{20}=10 mathrm{~cm}]
Ответ: 10 см
Высота прямоугольной трапеции
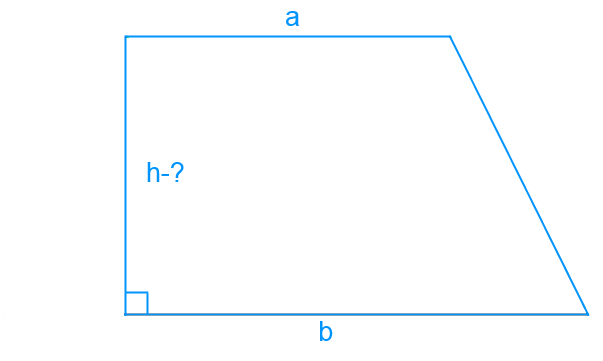
Определение
Диагональ — это сегмент, соединяющий пару противоположных вершин трапеции. Когда трапеция прямоугольная, используя диагональ, мы находим высоту данной фигуры.
Трапецию, одна из боковых сторон которой перпендикулярна основаниям, называют прямоугольной трапецией.
Таким образом, рассмотрим подобную трапецию ABCD, где AD — высота, AC — диагональ, DC-основание. Мы используем теорему Пифагора, которая говорит, что в прямоугольном треугольнике ADC квадрат гипотенузы AC равен сумме квадратов его сторон — катетов AB и BC.
Тогда мы сможем написать:
AC² = AD² + DC².
AD — это катет треугольника, сторона трапеции и, одновременно, ее высота. Так как отрезок перпендикулярен основаниям. Длина катета будет находиться как:
[A D=sqrt{left(A C^{2}-D C^{2}right)}]
Таким образом, у нас есть формула, которая поможет при вычислении найти высоту трапеции AD.
Пример 3
Основания трапеции с прямым углом(DC) равно 14 см, а ее диагональ (AC) равна 15 см, мы будем использовать теорему Пифагора для получения высоты (сторона AD).
Пусть x — неизвестная часть прямоугольного треугольника (AD), тогда
[A C^{2}=A D^{2}+D C^{2}] может быть записан
[15^{2}=14^{2}+x^{2}]
[x=sqrt{left(15^{2}-14^{2}right)}=sqrt{(225-196)}=sqrt{29} mathrm{см}]
Ответ: [sqrt{29} mathrm{см}], что составляет приблизительно 5,385 см
Нет времени решать самому?
Наши эксперты помогут!
Нахождение высоты через стороны
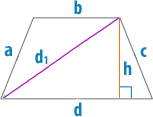
Существует еще один способ найти высоту — через стороны. Помимо высоты в трапеции стоит провести также ее диагональ, которая образует треугольник с прямым углом и даст возможность найти высоты несколькими различными способами через различные треугольники.
Если выразить все длины сторон таких треугольников через стороны трапеции и привести подобные слагаемые, то получится следующая формула:
[mathrm{h}=sqrt{C^{2}-left(frac{(a-b)^{2}+e^{2} d^{2}}{2(a-b)}right)^{2}}]
Пример 4
Дана трапеция, в ней известны основания a и b. Эти основания соответственно равны 4,5 см и 2,5 см. Известны и ее боковые стороны d и c, которые равны 2 см и используем формулу:
[h=sqrt{2^{2}-left(frac{(4,5-2,5)^{2}+2^{2}-2 sqrt{2}^{2}}{2(4,5-2,5)}right)^{2}}=sqrt{4}=2 см]
Ответ: h=2 см.
Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции
Определение.
Прямоугольная трапеция — это трапеция у котрой одна из боковых стороны перпендикулярна основам.
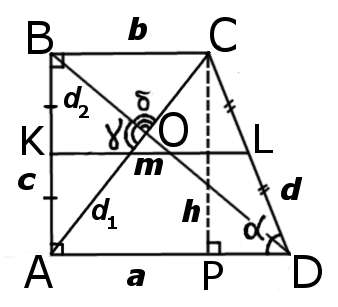 |
| Рис.1 |
Признаки прямоугольной трапеции
Трапеция будет прямоугольной если выполняется одно из этих условий:
1. В тапеции есть два смежных прямых угла:
∠BAD = 90° и ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:
AB ┴ BC, AB ┴ AD
Основные свойства прямоугольной трапеции
1. В трапеции есть два смежных прямых угла:
∠BAD = ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:
AB ┴ BC ┴ AD
3. Высота равна меньшей боковой стороне:
h = AB
Стороны прямоугольной трапеции
Формулы длин сторон прямоугольной трапеции:
1. Формулы длины оснований через стороны и угол при нижнем основании:
a = b + d cos α = b + c ctg α = b + √d 2 – c2
b = a – d cos α = a – c ctg α = a – √d 2 – c2
2. Формулы длины оснований через стороны, диагонали и угол между ними:
| a = | d1d2 | · sin γ – b = | d1d2 | · sin δ – b |
| c | c |
| b = | d1d2 | · sin γ – a = | d1d2 | · sin δ – a |
| c | c |
3. Формулы длины оснований трапеции через площадь и другие стороны:
| a = | 2S | – b b = | 2S | – a |
| c | c |
4. Формула боковой стороны через другие стороны и угол при нижнем основании:
c = √d 2 – (a – b)2 = (a – b) tg α = d sin α
5. Формулы боковой стороны через основы, диагонали и угол между ними:
| c = | d1d2 | · sin γ = | d1d2 | · sin δ |
| a + b | a + b |
6. Формулы боковой стороны через площадь, основы и угол при нижнем основании:
| d = | S | = | 2S |
| m sin α | (a + b) sin α |
7. Формула боковой стороны через другие стороны, высоту и угол при нижнем основании:
| d = | a – b | = | c | = | h | = √c2 + (a – b)2 |
| cos α | sin α | sin α |
Средняя линия прямоугольной трапеции
Формулы длины средней линии прямоугольной трапеции:
1. Формулы средней линии через основание, высоту (она же равна стороне c ) и угол α при нижнем основании:
| m = | a – h · | ctg α | = | b + h · | ctg α |
| 2 | 2 |
2. Формулы средней линии через основания и боковые стороны сторону:
| m = | a – | √d 2 – c2 | = | b + | √d 2 – c2 |
| 2 | 2 |
Примечание. Это часть урока с задачами по геометрии (раздел прямоугольная трапеция). Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. В задачах вместо символа “квадратный корень” применяется функция sqrt(), в которой sqrt – символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак “√”
См. также: трапеция и ее свойства.
Прямоугольная трапеция
Прямоугольная трапеция – это трапеция, у которой хотя бы один из углов прямой (классическое определение)
Примечание. На самом деле, у прямоугольной трапеции, как минимум, два прямых угла (см. ниже – свойства)
Другие определения:
- Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
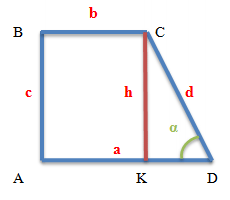
Формулы для прямоугольной трапеции
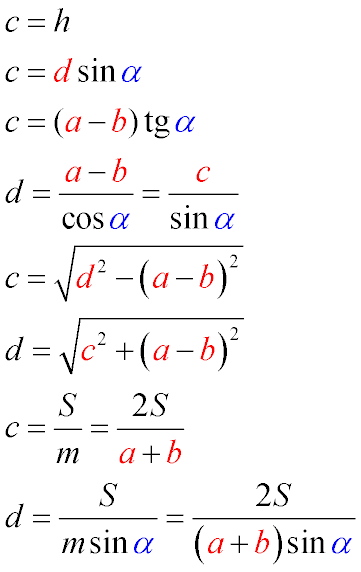
a и b – основания трапеции
с – боковая сторона прямоугольной трапеции, перпендикулярная основаниям
d – боковая сторона трапеции, не являющаяся перпендикулярной основаниям
α – острый угол при большем основании трапеции
m – средняя линия трапеции
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна высоте трапеции (Формула 1)
Боковая сторона прямоугольной трапеции,
перпендикулярная
основаниям, равна произведению синуса острого угла при большем основании на длину второй боковой стороны. (Треугольник CKD – прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)
Боковая сторона,
перпендикулярная
основаниям, равна произведению разности оснований на тангенс острого угла при большем основании. (Треугольник CKD – прямоугольный. Поскольку трапеция – прямоугольная, то длина KD – это и есть разность оснований, а h/KD=tgα по определению тангенса, а c=h, откуда с/KD=tgα) (Формула 3)
Боковая сторона, которая
не перпендикулярна
основаниям, равна частному разности оснований к косинусу острого угла при большем основании или частному высоты трапеции и синуса острого угла при большем основании. (разность оснований равна KD. В прямоугольном треугольнике CKD по определению косинуса cos α = KD / d, откуда и проистекает искомая формула) (Формула 4)
Боковая сторона прямоугольной трапеции, которая
не перпендикулярна
основаниям, равна корню квадратному из разности квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее – следствие из теоремы Пифагора – из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
Боковая сторона прямоугольной трапеции,
перпендикулярная
основаниям, равна корню квадратному из суммы квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, прямоугольный, далее – следствие из теоремы Пифагора – находим сумму квадратов катетов и извлекаем из полученного выражения квадратный корень) (Формула 6)
Боковая сторона прямоугольной трапеции,
перпендикулярная
основаниям, равна частному от деления двойной площади трапеции на сумму ее оснований. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 7)
Боковая сторона прямоугольной трапеции, которая
не перпендикулярна
основаниям, равна частному от деления двойной площади трапеции на произведение суммы ее оснований и синуса острого угла при основании. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)
Так как прямоугольная трапеция – это частный случай трапеции, то остальные формулы и свойства можно посмотреть в разделе “Трапеция”.
Свойства прямоугольной трапеции
- У прямоугольной трапеции два угла обязательно прямые
- Оба прямых угла прямоугольной трапеции обязательно принадлежат смежным вершинам
- Оба прямых угла в прямоугольной трапеции обязательно прилежат к одной и той же боковой стороне
- Диагонали прямоугольной трапеции образуют с одной из боковых сторон прямоугольный треугольник
- Длина боковой стороны трапеции, перпендикулярной основаниям равна ее высоте
- У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона – наклонная к основаниям
- У прямоугольной трапеции два угла прямые, а два других – острый и тупой
Задача
В прямоугольной трапеции большая боковая сторона равна сумме оснований, высота равна 12 см. Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Решение.
Обозначим трапецию как ABCD. Обозначим длины оснований трапеции как a (большее основание AD) и b (меньшее основание BC). Пусть прямым углом будет
∠A.
Площадь прямоугольника, стороны которого равны основаниям трапеции, будет равна
S = ab
Из вершины C верхнего основания трапеции ABCD опустим на нижнее основание высоту CK. Высота трапеции известна по условию задачи. Тогда, по теореме Пифагора
CK2 + KD
2 = CD2
Поскольку большая боковая сторона трапеции по условию равна сумме оснований, то CD = a + b
Поскольку трапеция прямоугольная, то высота, проведенная из верхнего основания трапеции разбивает нижнее основание на два отрезка
AD = AK + KD. Величина первого отрезка равна меньшему основанию трапеции, так как высота образовала прямоугольник ABCK, то есть BC = AK = b, следовательно, KD будет равен разности длин оснований прямоугольной трапеции KD = a – b.
то есть
122 + (a – b)2 = (a + b)2
откуда
144 + a2 – 2ab + b2 = a2 + 2ab + b2
144 = 4ab
Поскольку площадь прямоугольника S = ab (см. выше), то
144 = 4S
S = 144 / 4 = 36
Ответ: 36 см
2 .
0
Диагонали трапеции |
Описание курса
| Равнобокая (равнобедренная) трапеция
Нахождение высоты прямоугольной трапеции
В данной публикации мы рассмотрим различные формулы, с помощью которых можно вычислить высоту прямоугольной трапеции.
Напомним, в прямоугольной трапеции одна из боковых сторон перпендикулярна ее основаниями, и потому одновременно является высотой фигуры.
Нахождение высоты прямоугольной трапеции
Через длины сторон
Зная длины обоих оснований и большей боковой стороны прямоугольной трапеции, можно найти ее высоту (или меньшую боковую сторону):
Данная формула следует из теоремы Пифагора. В данном случае высота h – это неизвестный катет прямоугольного треугольника, гипотенуза которого равняется d, а известный катет – разности оснований, т.е. (a-b).
Через основания и прилежащий угол
Если даны длины оснований и любой из прилежащих к ним острых углов, то вычислить высоту прямоугольной трапеции можно по формуле:
Через боковую сторону и прилежащий угол
Если известна длина боковой стороны прямоугольной трапеции и прилежащий к ней угол (любой), найти высоту фигуры удастся таким образом:
Примечание: с помощью этой формулы можно, в т.ч., доказать, что меньшая боковая сторона – это и есть высота трапеции:
Через диагонали и угол между ними
При условии, что известны длины оснований прямоугольной трапеции, диагонали и угол между ними, рассчитать высоту фигуры можно так:
Если вместо суммы оснований известна длина средней линии, то формула примет вид:
m – средняя линия, которая равна половине суммы оснований, т.е.m = (a+b) /2.
Через площадь и основания
Если известна площадь прямоугольной трапеции и длина ее оснований (или средней линии), найти высоту можно таким образом:
Свойства прямоугольной трапеции
В данной статье мы расскажем Вам о свойствах прямоугольной трапеции, как обычной, так и той, в которую вписана окружность.
Для начала напомним некоторые основные определения.
Трапеция – это четырехугольник, имеющий 2 параллельные друг другу стороны, причем 2 другие стороны параллельными не являются.
Прямоугольная трапеция – это такая трапеция, одна из боковых сторон которой перпендикулярна ее основаниям (изображена на рис.).
Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон фигуры (на рис. EF).
Основные свойства прямоугольной трапеции
- Средняя линия EF равна половине суммы ее оснований BC и AD.
- точка пересечения (H) диагоналей прямоугольной трапеции AC и BD;
- точка пересечения (E) продолжений боковых сторон трапеции AB и CD;
- середины (F и G) оснований трапеции BC и AD.
Данным свойством обладает как прямоугольная, так и равносторонняя трапеция.
Свойства прямоугольной трапеции, в которую вписана окружность
SABCD = BC * AD
Узнать подробнее о свойствах трапеции с прямым углом, в которую вписана окружность, а также ознакомиться с доказательствами этих свойств, можно на сайте uznateshe.ru.
Понравилась статья, расскажите о ней друзьям:
Узнать ещё
Знание — сила. Познавательная информация
В прямоугольную трапецию вписана окружность
Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства.
1. Сумма оснований трапеции равна сумме боковых сторон.
2. Расстояния от вершины трапеции до точек касания вписанной окружности равны.
3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности.
4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
5. Если точка касания делит боковую сторону на отрезки m и n, то радиус вписанной окружности равен
И еще два полезных свойства прямоугольной трапеции, в которую вписана окружность:
1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r).
2) Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований.
Площадь трапеции равна произведению полусуммы ее оснований на высоту:
Обозначим CF=m, FD=n. Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а
[spoiler title=”источники:”]
http://people-ask.ru/nauki/geometriya/svojstva-pryamougolnoj-trapecii
[/spoiler]













