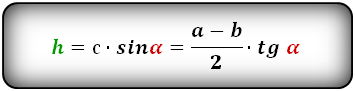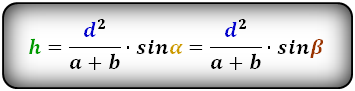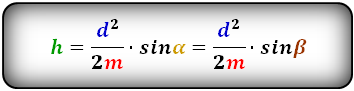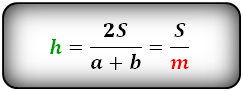В данной публикации мы рассмотрим различные формулы, с помощью которых можно вычислить высоту равнобедренной (равнобокой) трапеции.
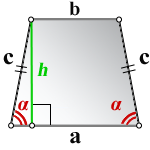
Напомним, высотой трапеции называется перпендикуляр, соединяющий оба ее основания. Также, в равнобедренной трапеции боковые стороны равны.
-
Нахождение высоты равнобедренной трапеции
- Через длины сторон
-
Через боковую сторону и прилежащий угол
- Через основания и прилежащий угол
- Через площадь и основания
- Через диагонали и угол между ними
Нахождение высоты равнобедренной трапеции
Через длины сторон
Зная длины всех сторон равнобедренной трапеции, вычислить ее высоту можно, используя формулу ниже:
Через боковую сторону и прилежащий угол
Если известна длина боковой стороны равнобедренной трапеции и угол между ней и основанием фигуры, найти высоту можно следующим образом:
Через основания и прилежащий угол
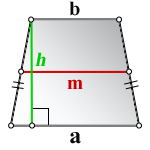
Вычислить высоту трапеции можно, если известны длины ее оснований и угол при любом из оснований (например, при большем).
Через площадь и основания
Также высоту равнобедренной трапеции удастся найти через ее площадь и длины оснований:
Данная формула может быть представлена в другом виде, если вместо оснований дана средняя линия (m).
m – средняя линия, равняется полусумме оснований, т.е. m = (a+b)/2.
Через диагонали и угол между ними
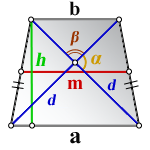
И еще один способ вычислить высоту равнобедренной трапеции, если известны ее диагонали (которые имеют одинаковую длину), угол между ними и основания.
Та же самая формула, но со средней линией (m) вместо суммы оснований:
Примечание: если диагонали равнобедренной трапеции взаимно перпендикулярны, то ее высота равняется половине суммы оснований или, другими словами, средней линии.
1. Формула высоты равнобедренной трапеции через стороны и углы при основании
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α – угол при нижнем основании
h – высота трапеции
Формулы длины высоты, (h ):
2. Формула высоты равнобедренной трапеции через диагонали и углы между ними
d – диагонали трапеции
α , β – углы между диагоналями
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
3. Формула высоты равнобедренной трапеции через площадь
S – площадь трапеции
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 10 октября 2013
-
Обновлено: 13 августа 2021
Как найти высоту трапеции
Анна Кирпиченкова
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
На этой странице вы узнаете, как найти высоту трапеции через стороны, а также как рассчитать высоту равнобедренной трапеции, зная среднюю линию и площадь. Также на страницу добавлены онлайн-калькуляторы для расчёта высоты трапеции.
Определение 1
Трапеция — это плоский геометрический объект, состоящий из двух параллельных и не равных друг другу отрезков-оснований и соединяющих их боковых сторон.
Для того чтобы рассчитать высоту трапеции, зная стороны, введите заданные значения в поля для ввода.
Высота трапеции через стороны
Высота трапеции через стороны рассчитывается по формуле:
$h = sqrt{b^2 – (frac{(a – d)^2 + b^2 – c^2}{2 cdot (a – d)})^2}$, где
$a$ — основание большего размера;
$d$ — основание меньшего размера;
$b$ — первая боковая сторона;
$c$ — вторая боковая сторона.
Пример 1
Задача
Дана трапеция с основаниями $a$ и $d$, равными $4.5$ и $2.5$ см и боковыми сторонами $b, c$, равными $2$ и $2sqrt2$ см. Найдите, чему равна высота трапеции $h$.
Решение:
Воспользуемся вышеприведённой формулой:
$h = sqrt{2^2 – (frac{(4.5 – 2.5)^2 + 2^2 – (2sqrt2)^2}{2 cdot (4.5 — 2.5)})^2} = sqrt{4 – (frac{4 + 4 — 8}{4}} = 2$ см.
Проверим полученное значение с помощью онлайн-калькулятора. Результат совпадает, а значит, задача решена верно.
Ниже приведён другой калькулятор, осуществляющий нахождение высоты равнобедренной трапеции через её площадь и среднюю линию.
Высота равнобедренной трапеции через среднюю линию и площадь
Если известна площадь равнобедренной трапеции и длина её средней линии, то высоту можно рассчитать по формуле:
$h = frac{S}{m}$, где
$m$ — средняя линия трапеции;
$S$ — её площадь.
Рассмотрим на примере, как найти высоту равнобедренной трапеции, если известны основания.
Пример 2
Задача
Дана равнобедренная трапеция с основаниями $a$ и $d$, соответственно равными $3$ и $5$ см, и площадью, равной $8$ $см^2$. Найдите, чему равна высота трапеции.
Решение:
Найдём среднюю линию трапеции:
$m = frac{a + d}{2} = frac{3 + 5}{2} = 4$ см.
Теперь сосчитаем высоту трапеции:
$h = frac{8}{4} = 2$ см.
Результаты совпадают с решением онлайн-калькулятора, а значит, ответ — верный.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 07.07.2019
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
Определение.
Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.
На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.
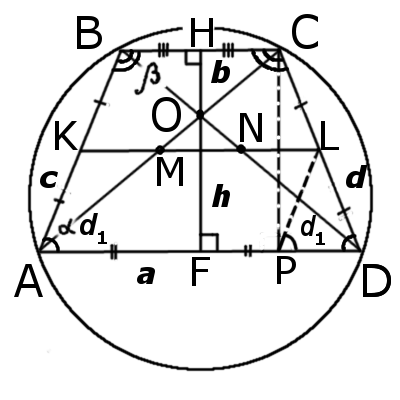 |
| Рис.1 |
Признаки равнобедренной трапеции
Трапеция будет равнобедренной если выполняется одно из этих условий:
1. Углы при основе равны:
∠ABC = ∠BCD и ∠BAD = ∠ADC
2. Диагонали равны:
AC = BD
3. Одинаковые углы между диагоналями и основаниями:
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
4. Сумма противоположных углов равна 180°:
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
5. Вокруг трапеции можно описати окружность
Основные свойства равнобедренной трапеции
1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:
AB = CD = m
3. Вокруг равнобедренной трапеции можно описать окружность
4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):
h = m
5. Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:
SABCD = h2
6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:
h2 = BC · AD
7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:
AC2 + BD2 = AB2 + CD2 + 2BC · AD
8. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:
HF ┴ BC, HF ┴ AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
1. Формулы длины сторон через другие стороны, высоту и угол:
a = b + 2h ctg α = b + 2c cos α
b = a – 2h ctg α = a – 2c cos α
| c = | h | = | a – b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d12 – c2 | b = | d12 – c2 | c = √d12 – ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | – b b = | 2S | – a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
1. Формула определения длины средней линии через основания, высоту и угол при основании:
m = a – h ctg α = b + h ctg α = a – √c2 – h2 = b + √c2 – h2
2. Формула средней линии трапеции через площадь и сторону:
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a – b | tg β | = c sin β |
| 2 |
Диагонали равнобедренной трапеции
Диагонали равнобедренной трапеции равны:
d1 = d2
Формулы длины диагоналей равнобедренной трапеции:
1. Формула длины диагонали через стороны:
d1 = √с2 + ab
2. Формулы длины диагонали по теореме косинусов:
d1 = √a2 + c2 – 2ac cos α
d1 = √b2 + c2 – 2bc cos β
3. Формула длины диагонали через высоту и среднюю линию:
d1 = √h2 + m2
4. Формула длины диагонали через высоту и основания:
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √4c2 – (a – b)2 |
| 4 |
2. Формула площади через стороны и угол:
S = (b + c cos α) c sin α = (a – c cos α) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = (a + b) · r = √ab·c = √ab·m
6. Формула площади через диагонали и угол между ними:
| S = | d12 | · sin γ | = | d12 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту:
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p – a)(p – c)(p – d1) |
где
a – большее основание
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 декабря 2021 года; проверки требуют 4 правки.
| Равнобедренная трапеция | |
|---|---|
 |
|
| Тип | четырёхугольник, трапеция |
| Рёбра | 4 |
| Вид симметрии | Dih2, [ ], (*), порядок 2 |
| Двойственный многоугольник | дельтоид |
| Свойства | |
| выпуклый, вписанный |
В евклидовой геометрии равнобедренная трапеция — это выпуклый четырёхугольник с осью симметрии, проходящей через середины двух противоположных сторон. Этот четырёхугольник является частным случаем трапеций. В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (боковые) имеют одинаковые длины (свойство, которому удовлетворяет также параллелограмм). Диагонали также имеют одинаковые длины. Углы при каждом основании равны и углы при разных основаниях являются смежными (в сумме дающие 180º).
Специальные случаи[править | править код]
Прямоугольники и квадраты обычно рассматриваются как специальные случаи равнобедренных трапеций, хотя в некоторых источниках они таковыми не считаются.
Другим специальным случаем является трапеция с 3 равными сторонами. В англоязычной литературе её называют trilateral trapezoid (трёхсторонняя трапеция) [1], trisosceles trapezoid (триравнобедренная трапеция) [2] или, реже, symtra [3]. Такую трапецию можно рассматривать как отсечение 4 последовательных вершин от правильного многоугольника, имеющего 5 или более сторон.
Самопересечения[править | править код]
Любой несамопересекающийся четырёхугольник с единственной осью симметрии должен быть либо равнобедренной трапецией, либо дельтоидом[3]. Однако, если разрешить самопересечение, множество симметричных четырёхугольников нужно расширить включением в него самопересекающиеся равнобедренные трапеции, в которых пересекающиеся стороны равны, а две другие стороны параллельны, и антипараллелограммы, у которых противоположные стороны имеют равные длины.
У любого антипараллелограмма выпуклая оболочка является равнобедренной трапецией и антипараллелограмм может быть получен из диагоналей равнобедренной трапеции[4].

|

|

|
| Выпуклая равнобедренная трапеция |
Самопересекающаяся равнобедренная трапеция |
Антипараллелограмм |
|---|
Свойства[править | править код]
Если четырёхугольник является трапецией, не обязательно проверять, равны ли боковые стороны (и недостаточно, поскольку ромбы, являющиеся специальными случаями трапеций с боковыми сторонами равной длины, но у него нет осевой симметрии через середины оснований). Любое из следующих свойств выделяет равнобедренную трапецию от других трапеций:
- Диагонали имеют одинаковую длину.
- Углы при основании равны.
- Отрезок, соединяющий середины параллельных сторон, перпендикулярен им.
- Противоположные углы дополнительны (до 180º), из чего, в свою очередь, следует, что равнобедренные трапеции являются вписанными четырёхугольниками.
- Диагонали делятся точкой пересечения на попарно равные отрезки. В терминах рисунка ниже, AE = DE, BE = CE (и AE ≠ CE, если хотят исключить прямоугольники).
Если прямоугольники включаются в класс трапеций, то можно определить равнобедренную трапецию как “вписанный четырёхугольник с равными диагоналями” [5], как “вписанный четырёхугольник с парой параллельных сторон”, или как “выпуклый четырёхугольник с осью симметрии, проходящей через середины противоположных сторон”.
Углы[править | править код]
В равнобедренной трапеции углы при основаниях попарно равны. На рисунке ниже углы ∠ABC и ∠DCB являются одинаковыми тупыми углами, а углы ∠BAD и ∠CDA являются одинаковыми острыми углами.
Поскольку прямые AD и BC параллельны, углы, принадлежащие противоположным основаниям, являются дополнительными, то есть ∠ABC + ∠BAD = 180°.
Диагонали и высота[править | править код]
Другая равнобедренная трапеция.
Диагонали равнобедренной трапеции равны. То есть любая равнобедренная трапеция является равнодиагональным четырёхугольником. Однако диагонали равнобедренной трапеции делятся в одной и той же пропорции. На рисунке диагонали AC и BD имеют одинаковую длину (AC = BD) и делят друг друга на отрезки той же длины (AE = DE и BE = CE).
Отношение, в котором делятся диагонали, равно отношению длин параллельных сторон, то есть
Длина каждой диагонали, согласно следствию из теоремы Птолемея, задаётся формулой
,
где a и b — длины параллельных сторон AD и BC, а c — длина каждой боковой стороны AB и CD.
Высота, согласно теореме Пифагора, задаётся формулой
Расстояние от точки E до основания AD задаётся формулой
,
где a и b — длины оснований AD и BC, а h — высота трапеции.
Площадь[править | править код]
Площадь равнобедренной (а также любой) трапеции равна половине произведения суммы оснований на высоту. На рисунке, если мы примем AD = a, BC = b, а высота h равна длине отрезка между прямыми AD и BC (перпендикулярного им), то площадь K задаётся формулой:
Если вместо высоты трапеции известны длины боковых сторон AB =CD = c, то площадь можно вычислить по формуле Брахмагупты площади вписанных четырёхугольников. Равенство двух боковых сторон упрощает формулу до
где 
Радиус описанной окружности[править | править код]
Радиус описанной окружности задаётся формулой[6]
Для прямоугольника, в котором a = b, формула упрощается до 
См. также[править | править код]
- Равнобедренная описанная трапеция
Литература[править | править код]
- George Bruce Halsted. Elementary Synthetic Geometry. — J. Wiley & sons, 1896..
- William Dwight Whitney, Benjamin Eli Smith. The Century Dictionary and Cyclopedia. — The Century co., 1911..
Примечания[править | править код]
- ↑ Michael de Villiers, Hierarchical Quadrilateral Tree [1] Архивная копия от 22 декабря 2014 на Wayback Machine
- ↑ isosceles trapezoid. Дата обращения: 25 сентября 2016. Архивировано 26 августа 2016 года.
- ↑ 1 2 Halsted, 1896, с. 49–53.
- ↑ Whitney, Smith, 1911, с. 1547.
- ↑ Mzone.mweb.co.za. Дата обращения: 25 сентября 2016. Архивировано 19 июля 2011 года.
- ↑ Trapezoid at Math24.net: Formulas and Tables [2] Архивная копия от 28 июня 2018 на Wayback Machine Accessed 1 July 2014.
Ссылки[править | править код]
- Some engineering formulas involving isosceles trapezoids