Как посчитать высоту равнобедренного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать высоту равнобедренного треугольника
Чтобы посчитать чему равна высота равнобедренного треугольника просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы вычислить высоту равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
- длину двух равных сторон (a) и длину основания (b)
- длину двух равных сторон (a) и угол α
- длину двух равных сторон (a) и угол β
- длину основания (b) и угол α
- длину основания (b) и угол β
Введите их в соответствующие поля и получите результат.
Если известны длина стороны а и основания b
Чему равна высота h равнобедренного треугольника если длина сторон
a =
, а длина основания
b =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и длина основания b?
Формула
h = √a2 – (b/2)2
Пример
Если сторона a = 10 см, а сторона b = 5 см, то:
h = √102 – (5/2)2 = √100 – 6.25 ≈ 9.68 см
Если известны длина стороны а и угол α
Чему равна высота h равнобедренного треугольника если длина сторон
a =
, а угол
α =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол α?
Формула
h = a⋅sin α
Пример
Если сторона a = 5 см, а ∠α = 45°, то:
h = 5⋅sin 45 ≈ 3,53 см
Если известны длина стороны а и угол β
Чему равна высота h равнобедренного треугольника если длина сторон
a =
, а угол
β =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол β?
Формула
h = a⋅cos β/2
Пример
Если сторона a = 5 см, а ∠β = 30°, то:
h = 5⋅cos 30/2 ≈ 4.83 см
Если известны длина стороны b и угол α
Чему равна высота h равнобедренного треугольника если длина основания
b =
, а угол
α =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол α?
Формула
h = b/2⋅tg α
Пример
Если сторона b = 20 см, а ∠α = 35°, то:
h = 20/2⋅tg 35 = 10⋅0.7 = 7 см
Если известны длина стороны b и угол β
Чему равна высота h равнобедренного треугольника если длина основания
b =
, а угол
β =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол β?
Формула
h = b/2⋅ctg β/2
Пример
Если сторона b = 15 см, а ∠β = 40°, то:
h = 15/2⋅ctg 40/2 = 7.5⋅2.7474 ≈ 20.6 см
См. также
Равнобедренным треугольником называется такой треугольник, у которого две из трех сторон равны между собой. Равные стороны считаются боковыми сторонами а, а третья сторона в называется основанием равнобедренного треугольника.
Соответственно, в таком треугольнике можно провести три высоты, две из которых будут равны между собой, аналогично сторонам – это высоты, опущенные на боковую сторону треугольника а, а третья высота опускается на основание. Высота треугольника проводится из угла треугольника к противолежащей стороне под прямым углом. Большинство задач с высотой треугольника решаются через прямоугольные треугольники, которые она образует.
Рассмотрим каждый случай по отдельности.
Высота равнобедренного треугольника, опущенная на основание, обладает рядом индивидуальных свойств, присущих только ей и не распространяющихся на другие высоты в таком треугольнике. В частности, высота, проведенная к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой, проведенным к основанию, следовательно, она не только образует прямой угол с основанием, но и делит его на две равные части, как медиана, и аналогично делит угол пополам, как биссектриса. В итоге, высота является своеобразной осью симметрии треугольника и разделяет его на два конгруэнтных прямоугольных треугольника. В таком треугольнике высота является катетом, и чтобы найти ее длину необходимо соотнести стороны равнобедренного треугольника со сторонами прямоугольного. Боковая сторона равнобедренного треугольника становится гипотенузой, а чтобы определить второй катет, основание равнобедренного треугольника нужно разделить пополам, по свойству медианы.
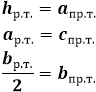
Длина высоты равнобедренного треугольника равна по теореме Пифагора квадратному корню из суммы квадрата боковой стороны равнобедренного треугольника и четверти квадрата основания равнобедренного треугольника:
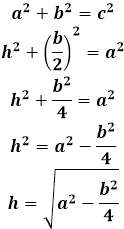
Второй случай, когда условиями задачи нужно найти высоту, опущенную на боковую сторону равнобедренного треугольника, раскрывается проще всего через площадь треугольника.
Площадь любого треугольника можно найти несколькими способами – например, через три стороны треугольника по формуле Герона, или через высоту, умножив ее на половину стороны, на которую она опущена. И тем, и другим способом получаются одинаковые значения площади, следовательно обе эти формулы можно друг к другу приравнять и отсюда вывести окончательную формулу высоты, опущенную на боковую сторону равнобедренного треугольника.
Формула Герона для равнобедренного треугольника будет иметь несколько упрощенный вид за счет того, что значения боковых сторон повторяются:
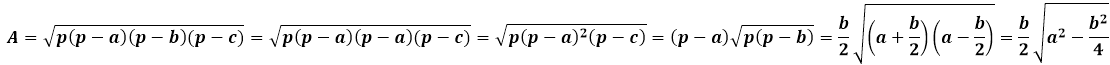
Площадь равнобедренного треугольника через высоту, опущенную к боковой стороне
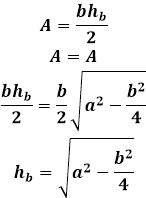
Эту же формулу можно применять для нахождения любой высоты в равнобедренном треугольнике, если поменять в формуле соответствующие стороны местами.
Формула высоты равнобедренного треугольника через боковую сторону и угол при основании α: h=a sinα
Формула через боковую сторону и угол напротив основания β:
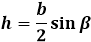
Формула через основание и угол при нем α:
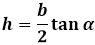
через основание и угол противолежащий ему β:
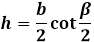
Высота равнобедренного треугольника, формула
Высота равнобедренного треугольника из теоремы Пифагора, формула
[
h^2+Big(frac{b}{2}Big)^2=a^2 \
h^2=a^2-Big(frac{b}{2}Big)^2
]
[
h=sqrt{a^2-frac{b^2}{4}}
]
Высота равнобедренного треугольника по формуле Герона, формула
[
h = frac{ 2 sqrt{p(p-a)(p-b)(p-a)}}{b}
]
где
[
p=frac{1}{2}(a+b+a)=a+frac{b}{2}
]
после подстановки коэффициента p в формулу получим
[
h = frac{ 2 sqrt{(a+frac{b}{2})(a+frac{b}{2}-a)(a+frac{b}{2}-b)(a+frac{b}{2}-a)}}{b}
]
[
h = frac{ 2 sqrt{(a+frac{b}{2})(frac{b}{2})(a-frac{b}{2})(frac{b}{2})}}{b}
]
по формулам сокращенного умножения, разность квадратов получим
[
Big(a+frac{b}{2}Big)Big(a-frac{b}{2}Big)=a^2-Big(frac{b}{2}Big)^2
]
далее вносим под корень 2 и знаменатель b
[
h = sqrt{frac{2^2(a^2-(frac{b}{2})^2)(frac{b}{2})^2}{b^2}}
]
после сокращений получим
[
h=sqrt{a^2-frac{b^2}{4}}
]
Вычислить, найти высоту равнобедренного треугольника по формуле (9)
Высота равнобедренного треугольника |
стр. 232 |
|---|
Высота равнобедренного треугольника


4.4
Средняя оценка: 4.4
Всего получено оценок: 96.
4.4
Средняя оценка: 4.4
Всего получено оценок: 96.
Из-за двух равных сторон, равнобедренный треугольник обладает рядом специфических свойств, за которые его очень любят составители задач. Рассмотрим, чем же выделяется высота равнобедренного треугольника и как ее лучше найти.

Материал подготовлен совместно с учителем первой категории Камушковой Натальей Владимировной.
Опыт работы учителем математики – 27 лет.
Определение
В общем случае, высота – это перпендикуляр, опущенный из вершины фигуры на противолежащую сторону. В равнобедренном треугольнике под высотой обычно подразумевают высоту, опущенную на основание.
Если по условию задачи нужно найти значение высоты равнобедренного треугольника без уточнений, какую именно требуется найти, то имеется в виду высота, опущенная на основание.
Необходимые теоремы
Для решения задач на определение высоты равнобедренного треугольника, нужно знать теорему Пифагора и свойство высоты равнобедренного треугольника.
Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Свойство: в равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
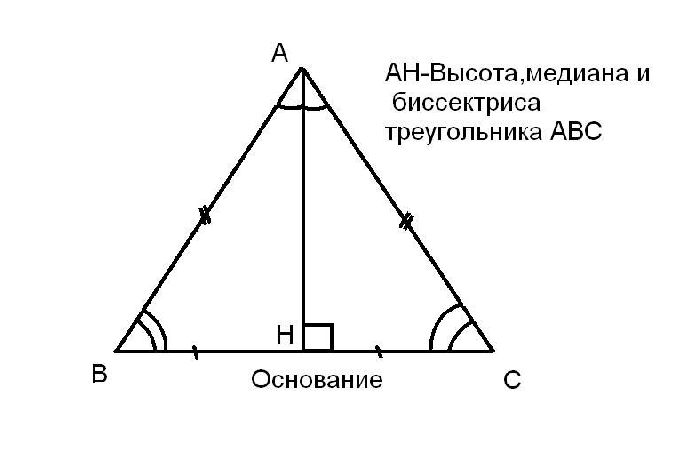
Из теоремы и свойства следует основная формула высоты равнобедренного треугольника. Рассмотрим равнобедренный треугольник АВС с высотой АН и основанием ВС. Тогда треугольник АВН является прямоугольным. Запишем значение высоты через теорему Пифагора, так как в треугольнике АВН высота АН является катетом.
$$АН=sqrt{АВ^2-BH^2}=sqrt{AB^2-({BCover{2}})^2}$$
$$ВН={1over2}*ВС$$, так как по свойству высоты равнобедренного треугольника АН является медианой. Это и есть формула высоты равнобедренного треугольника.
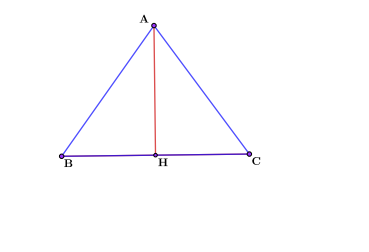
Задача
Решим задачу, где будет задействована не только высота, проведенная к основанию, но и другая высота. В равнобедренном треугольнике, как и в любом другом, их три. В задаче также будет применен способ нахождения высоты, который можно использовать для любого треугольника, а не только для равнобедренного.
В Равнобедренном треугольнике АВС с основанием ВС проведены высоты АН и ВР. Синус угла АСВ равен 0,6, а боковая сторона 5. Найти высоту ВР.
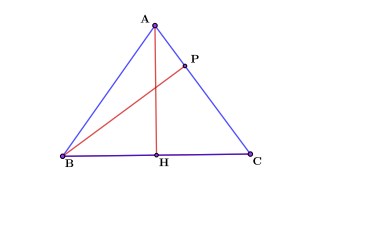
Для начала, необходимо найти значение высоты, проведенной к основанию и основание. Для этого обратим внимание на прямоугольный треугольник АСН. Воспользуемся определением синуса.
Синус угла это отношение противолежащего катета к гипотенузе. Нам известно значение синуса, значит:
$${АНover{АС}}=0,6$$ – из этого отношения выразим значение АН.
$$АН=0,6 *АС=0,6*5=3$$
Через теорему Пифагора найдем значение НС:
$$НС=sqrt{АС^2-AH^2}=sqrt{25-9}=sqrt{16}=4$$
Тогда основание равно:
$$ВС=ВН+НС=2*НС=2*4=8$$
Теперь найдем площадь треугольника:
$$S={1over2}*АН*ВС={1over2}*3*8=12$$
С другой стороны площадь можно найти и через высоту ВР.
$$S={1over2}*ВР*АС$$ – так как ВР это высота, проведенная к стороне АС.
Значит верно равенство:
$${1over2} *АН*ВС={1over2}*ВР*АС$$
$$АН*ВС=ВР*АС$$
$$ВР={{АН*ВС}over{АС}}={{3*8}over5}={24over5}=4,8$$

Что мы узнали?
Мы вывели формулу высоты прямоугольного треугольника. Определили, что высота в прямоугольном треугольнике может находиться любым способом, связанным с произвольным треугольником и решили интересную задачу на нахождение высоты треугольника.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 96.
А какая ваша оценка?
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
-
Нахождение высоты треугольника
- Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
- Высота в прямоугольном треугольнике
- Высота в равностороннем треугольнике
- Примеры задач
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны
![]()
где S – площадь треугольника.
2. Через длины всех сторон
![]()
где p – это полупериметр треугольника, который рассчитывается так:
![]()
3. Через длину прилежащей стороны и синус угла
![]()
4. Через стороны и радиус описанной окружности
![]()

где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:


Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
![]()
2. Через стороны треугольника
![]()
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
![]()

Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
![]()
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
![]()
