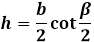Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.
2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности


где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:


Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:


Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Равнобедренный прямоугольный треугольник


Средняя оценка: 4.1
Всего получено оценок: 274.
Средняя оценка: 4.1
Всего получено оценок: 274.
И равнобедренный, и прямоугольный треугольник достаточно привычны любому, кто знаком с геометрией. Сочетание этих признаков встречается довольно редко и плохо поддается визуальному восприятию. Не всегда можно представить полный набор свойств такого треугольника, поэтому поговорим о нем более подробно.

Определение
Равнобедренный треугольник – это треугольник, боковые стороны которого равны. Прямоугольный треугольник содержит в себе прямой угол. Значит равнобедренный прямоугольный треугольник – это прямоугольный треугольник, катеты которого равны.
Гипотенуза прямоугольного треугольника всегда больше катета. Это следует из теоремы о соотношениях сторон и углов треугольника. Значит, в прямоугольном треугольнике только гипотенуза может быть основанием, а величина гипотенузы будет соответствовать длине основания.
Свойства
Поговорим подробнее о свойствах и формулах. Не совсем ясно, как будут проходить высоты в таком треугольнике, все привыкли пользоваться свойством, которое говорит о том, что в равнобедренном треугольнике высота, проведенная к основанию, совпадает с медианой и биссектрисой.
В равнобедренном прямоугольном треугольнике такая высота всегда будет направлена из прямого угла к гипотенузе. А две другие высоты будут совпадать с катетами.
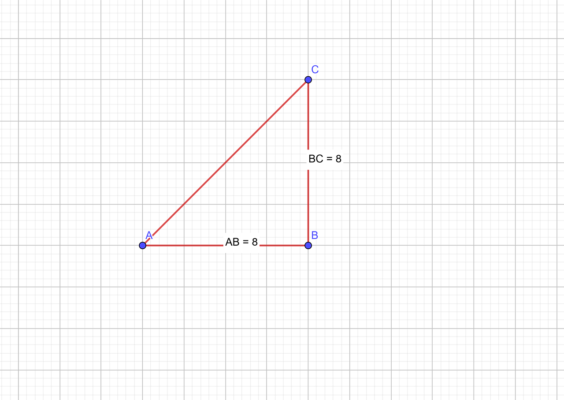 Рис. 2. Высота прямоугольного равнобедренного треугольника
Рис. 2. Высота прямоугольного равнобедренного треугольника
Если к гипотенузе прямоугольного равнобедренного треугольника провести высоту, то она разделит треугольник на два, равных между собой, равнобедренных прямоугольных треугольника.
Теорема Пифагора для равнобедренного треугольника выглядит немного упрощенной:
Квадрат гипотенузы равен удвоенному квадрату катета. Это значительно упрощает решение.
Вообще, любые задачи, связанные с прямоугольными равнобедренными треугольниками, решаются очень просто. Любого значения достаточно, чтобы определить все остальное. Значения любого из катетов достаточно, чтобы определить гипотенузу через упрощенную теорему Пифагора, а затем найти периметр и площадь прямоугольного равнобедренного треугольника.
Через гипотенузу можно найти катет и через тригонометрическую функцию, так как все углы прямоугольного равнобедренного треугольника заранее известны: один угол 90 градусов и два по 45.
 Рис. 3. Углы прямоугольного равнобедренного треугольника
Рис. 3. Углы прямоугольного равнобедренного треугольника
Разберем подробно, почему известны все углы. В любом прямоугольном треугольнике сумма острых углов равна 90 градусам. Это следует из общей суммы углов в треугольнике, которая всегда равна 180 градусам.
При этом углы при основании равнобедренного треугольника, а в нашем случае это всегда гипотенуза, всегда равны. Значит, чтобы найти каждый из острых углов при гипотенузе, нужно их сумму, т.е. 90 градусов, разделить пополам. Получается, что каждый из углов при гипотенузе прямоугольного равнобедренного треугольника будет равен 45 градусам.
Можно рассмотреть это свойство и с другой стороны: если сумма двух углов треугольника равняется 90 градусам и эти углы равны между собой, то этот треугольник является равнобедренным и прямоугольным.
Из этого же свойства вытекает равенство синусов и косинусов острых углов прямоугольного равнобедренного треугольника между собой, а также равенство их тангенсов и котангенсов.
То есть, синус любого острого угла прямоугольного равнобедренного треугольника равен косинусу любого острого угла данного треугольника и равен $$<sqrt<2>over2>$$. Тангенс любого острого угла прямоугольного равнобедренного треугольника равен котангенсу любого острого угла данного треугольника и равен 1.

Что мы узнали?
Мы подробно поговорили о всех взаимосвязях свойств прямоугольного и равнобедренного треугольника. А также о том, как эти связи проявляются в равнобедренном прямоугольном треугольнике. Разобрали в подробностях, почему любые задачи на нахождение параметров прямоугольного равнобедренного треугольника легко решаются и выделили основную и единственную проблему в решениях таких задач: трудность визуального восприятия.
Способы нахождения высоты треугольника: теорема и формула
Определение высоты треугольника
Геометрия, являющаяся разделом математики, изучает структуры в пространстве и на плоскости. Одним из типов таких фигур являются геометрические фигуры. К ним можно отнести квадрат, прямоугольник, круг, пятиугольник, треугольник и другие. Из них можно делать более сложные фигуры или оставлять в первоначальном виде.
Треугольником является фигура, относящаяся к классу простых фигур, которая образована тремя точками, находящимися не на одной прямой, и соединенными между собой тремя отрезками.
Треугольники могут быть:
- разными по величине углов: прямоугольными, тупоугольными и остроугольными;
- разными по числу равных сторон: равносторонними, равнобедренными и разносторонними.
Помимо трех сторон, важными элементами треугольников являются медианы, высоты и биссектрисы.
Высотой треугольника является перпендикуляр, опущенный из угла треугольника вниз, на противоположную сторону.
В геометрии высота треугольника обозначается буквой h.
В зависимости от типа треугольника высота может:
- падать на противоположную сторону — у остроугольного треугольника;
- находиться вне треугольника — у тупоугольного треугольника;
- совпадать с одной из сторон — у прямоугольного треугольника.
Чтобы сделать высоту графически явной и понятной на рисунке, ее нередко выделяют красной линией.
Для того чтобы определить графическое начертание высоты треугольника, необходимо:
- Найти вершину фигуры.
- Опустить вниз перпендикулярную линию к противоположной стороне.
- Продлить противоположную сторону до пересечения с высотой, если требуется.
Любой треугольник имеет 3 высоты — по числу углов. Их пересечение находится в точке ортоцентра, которая, в зависимости от типа треугольника, может находиться внутри треугольника, снаружи на пересечении продолжений высот или совпадать с вершиной прямого угла.
Все три высоты треугольника обратно пропорциональны сторонам, к которым опущены. Доказательством будет соотношение:
A × H A ÷ B × H B ÷ C × H C = 1 B C ÷ 1 A C ÷ 1 A B
Выглядеть графически это будет так:
Существует множество способов нахождения высоты треугольника в зависимости от имеющихся данных.
Через площадь и длину стороны, к которой опущена высота:
где S — уже известная площадь треугольника,
Через длины всех сторон:
h = 2 p p × a p × b p × c a
где a, b и c — стороны треугольника,
p — его полупериметр.
Данная формула подходит только для нахождения высоты разностороннего треугольника.
Через длину прилежащей стороны и синус угла:
s i n a — синус угла прилежащей стороны.
Данная формула подходит только для нахождения высоты разностороннего треугольника.
Через стороны и радиус описанной окружности.
Решать задачи с треугольником и описанной окружностью для нахождения высоты можно следующим образом:
где b, c — стороны разностороннего треугольника, к которым не опущена высота,
R — радиус описанной окружности.
Данная формула подходит только для нахождения высоты разностороннего треугольника.
Через длины отрезков, образованных на гипотенузе при проведении к ней высоты треугольника:
где C 1 и С 2 — длины отрезков, образованных на гипотенузе, проведенной к ней высотой.
Данная формула подходит только для нахождения высоты прямоугольного треугольника.
Нахождение высоты равнобедренного треугольника через основание и боковые стороны
Равнобедренным треугольником называют треугольник, имеющий одинаковые по длине катеты, которые образуют равные углы с основанием. В таком треугольнике высота будет опускаться ровно в середину основания, образуя с ним прямой угол.
Помимо высоты, проведенная линия будет являться также осью симметрии, биссектрисой вершинного угла и медианой.
Формула для нахождения высоты в этом случае:
где a — основание,
b — равные боковые стороны.
Свойства высоты в равностороннем треугольнике
Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.
Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.
Высоту в таком треугольнике можно найти с помощью следующей формулы:
где а — сторона равностороннего треугольника.
Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:
а — сторона правильного равностороннего треугольника.
Нахождение высоты прямоугольного треугольника через его катеты
Прямоугольным считается треугольник, у которого один из углов является прямым, то есть равным 90°. Высота, опущенная из такого угла, падает на гипотенузу треугольника и делит его на два прямоугольных треугольника, которые пропорциональны по отношению к большому треугольнику и друг к другу.
Важно отметить, что две другие высоты будут совпадать с катетами треугольника.
Найти высоту в прямоугольном треугольнике, можно через два его катета (a и b) и гипотенузу (c).
Причем гипотенуза также легко находится через катеты по теореме Пифагора:
Расчет высоты идет следующим образом:
где a, b и c — вышеупомянутые стороны треугольника.
[spoiler title=”источники:”]
http://obrazovaka.ru/matematika/ravnobedrennyy-pryamougolnyy-treugolnik-ploschad.html
http://wika.tutoronline.ru/geometriya/class/7/sposoby-nahozhdeniya-vysoty-treugolnika-teorema-i-formula
[/spoiler]
Как посчитать высоту равнобедренного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать высоту равнобедренного треугольника
Чтобы посчитать чему равна высота равнобедренного треугольника просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы вычислить высоту равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
- длину двух равных сторон (a) и длину основания (b)
- длину двух равных сторон (a) и угол α
- длину двух равных сторон (a) и угол β
- длину основания (b) и угол α
- длину основания (b) и угол β
Введите их в соответствующие поля и получите результат.
Если известны длина стороны а и основания b
Чему равна высота h равнобедренного треугольника если длина сторон
a =
, а длина основания
b =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и длина основания b?
Формула
h = √a2 – (b/2)2
Пример
Если сторона a = 10 см, а сторона b = 5 см, то:
h = √102 – (5/2)2 = √100 – 6.25 ≈ 9.68 см
Если известны длина стороны а и угол α
Чему равна высота h равнобедренного треугольника если длина сторон
a =
, а угол
α =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол α?
Формула
h = a⋅sin α
Пример
Если сторона a = 5 см, а ∠α = 45°, то:
h = 5⋅sin 45 ≈ 3,53 см
Если известны длина стороны а и угол β
Чему равна высота h равнобедренного треугольника если длина сторон
a =
, а угол
β =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол β?
Формула
h = a⋅cos β/2
Пример
Если сторона a = 5 см, а ∠β = 30°, то:
h = 5⋅cos 30/2 ≈ 4.83 см
Если известны длина стороны b и угол α
Чему равна высота h равнобедренного треугольника если длина основания
b =
, а угол
α =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол α?
Формула
h = b/2⋅tg α
Пример
Если сторона b = 20 см, а ∠α = 35°, то:
h = 20/2⋅tg 35 = 10⋅0.7 = 7 см
Если известны длина стороны b и угол β
Чему равна высота h равнобедренного треугольника если длина основания
b =
, а угол
β =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол β?
Формула
h = b/2⋅ctg β/2
Пример
Если сторона b = 15 см, а ∠β = 40°, то:
h = 15/2⋅ctg 40/2 = 7.5⋅2.7474 ≈ 20.6 см
См. также
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
-
Нахождение высоты треугольника
- Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
- Высота в прямоугольном треугольнике
- Высота в равностороннем треугольнике
- Примеры задач
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны
![]()
где S – площадь треугольника.
2. Через длины всех сторон
![]()
где p – это полупериметр треугольника, который рассчитывается так:
![]()
3. Через длину прилежащей стороны и синус угла
![]()
4. Через стороны и радиус описанной окружности
![]()

где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:


Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
![]()
2. Через стороны треугольника
![]()
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
![]()

Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
![]()
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
![]()
как найти высоту в равнобедренном прямоугольном треугольнике???
Виктория Ермоленко
Ученик
(172),
на голосовании
7 лет назад
Голосование за лучший ответ
Александр Лысенко
Ученик
(180)
7 лет назад
https://www.fxyz.ru/формулы_по_геометрии/плоские_фигуры/треугольник/высота_треугольника/высота_равнобедренного_треугольника/
hugo
Искусственный Интеллект
(193169)
7 лет назад
а чё дано?
Наталия Тузина
Просветленный
(49644)
7 лет назад
В прямоугольном треугольнике катет является высотой.
А если имеется ввиду высота к гипотенузе, то как в любом треугольнике.
Ольга Рыжова
Просветленный
(28669)
7 лет назад
В равнобедренном прямоугольном треугольнике высота, опущенная из прямого угла равна половине гипотенузы
Похожие вопросы
Равнобедренным треугольником называется такой треугольник, у которого две из трех сторон равны между собой. Равные стороны считаются боковыми сторонами а, а третья сторона в называется основанием равнобедренного треугольника.
Соответственно, в таком треугольнике можно провести три высоты, две из которых будут равны между собой, аналогично сторонам – это высоты, опущенные на боковую сторону треугольника а, а третья высота опускается на основание. Высота треугольника проводится из угла треугольника к противолежащей стороне под прямым углом. Большинство задач с высотой треугольника решаются через прямоугольные треугольники, которые она образует.
Рассмотрим каждый случай по отдельности.
Высота равнобедренного треугольника, опущенная на основание, обладает рядом индивидуальных свойств, присущих только ей и не распространяющихся на другие высоты в таком треугольнике. В частности, высота, проведенная к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой, проведенным к основанию, следовательно, она не только образует прямой угол с основанием, но и делит его на две равные части, как медиана, и аналогично делит угол пополам, как биссектриса. В итоге, высота является своеобразной осью симметрии треугольника и разделяет его на два конгруэнтных прямоугольных треугольника. В таком треугольнике высота является катетом, и чтобы найти ее длину необходимо соотнести стороны равнобедренного треугольника со сторонами прямоугольного. Боковая сторона равнобедренного треугольника становится гипотенузой, а чтобы определить второй катет, основание равнобедренного треугольника нужно разделить пополам, по свойству медианы.
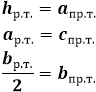
Длина высоты равнобедренного треугольника равна по теореме Пифагора квадратному корню из суммы квадрата боковой стороны равнобедренного треугольника и четверти квадрата основания равнобедренного треугольника:
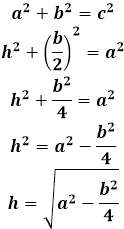
Второй случай, когда условиями задачи нужно найти высоту, опущенную на боковую сторону равнобедренного треугольника, раскрывается проще всего через площадь треугольника.
Площадь любого треугольника можно найти несколькими способами – например, через три стороны треугольника по формуле Герона, или через высоту, умножив ее на половину стороны, на которую она опущена. И тем, и другим способом получаются одинаковые значения площади, следовательно обе эти формулы можно друг к другу приравнять и отсюда вывести окончательную формулу высоты, опущенную на боковую сторону равнобедренного треугольника.
Формула Герона для равнобедренного треугольника будет иметь несколько упрощенный вид за счет того, что значения боковых сторон повторяются:
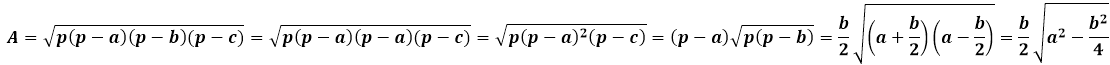
Площадь равнобедренного треугольника через высоту, опущенную к боковой стороне
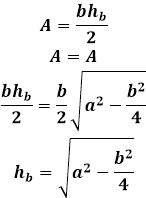
Эту же формулу можно применять для нахождения любой высоты в равнобедренном треугольнике, если поменять в формуле соответствующие стороны местами.
Формула высоты равнобедренного треугольника через боковую сторону и угол при основании α: h=a sinα
Формула через боковую сторону и угол напротив основания β:
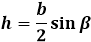
Формула через основание и угол при нем α:
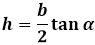
через основание и угол противолежащий ему β: