пусть высоты ромба будут А и В, а сторона ромба – С.
тогда:
периметр ромба равен 4С,
площадь ромба равна АВ/2.
также, по теореме Пифагора, квадрат стороны ромба равен сумме квадратов половин высот:
C^2 = (A/2)^2 + (B/2)^2
вам надо найти А и В.
у вас есть система уравнений
АВ/2 = “площади”,
(A/2)^2 + (B/2)^2 = (“периметр делёный на четыре”)^2.
решаете систему – получаете значение высот.
NaumenkoВысший разум (856096)
7 лет назад
тамор…. фи
удручающе нерациональное решение. слишком сложно.
но мбэто ваше хобби- не сделать простого- своей страницы.
и так накрутить в простой 2-х шаговой задаче…
незачет.
Tamop
Мыслитель
(5479)
это не решение, потому что оно выведено из ошибочного представления о вопросе задачи – я искал диагонали, а не высоту.
Высота ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти высоту ромба по известным элементам. Для нахождения высоты ромба введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.
Содержание
- Высота ромба через сторону и площадь
- Высота ромба через сторону и угол
- Высота ромба через диагонали
- Высота ромба через угол и противолежащую диагональ
- Высота ромба через угол и диагональ из данного угла
- Высота ромба через радиус вписанной в ромб окружности
1. Высота ромба через сторону и площадь
Пусть задан ромб (Рис.1).
Формула площади ромба через сторону и высоту имеет следующий вид:
Откуда легко вывести формулу высоты ромба через сторону и площадь:
2. Высота ромба через сторону и угол
Рассмотрим ромб со стороной a и углом α между сторонами (Рис.2). Выведем формулу вычисления высоты ромба через сторону и угол.
Проведем высоту AH. Для прямоугольного треугольника AHB применим теорему синусов:
Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:
Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого угла. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: (small angle C=180°-alpha.) Следовательно (small sin angle C=sin(180°-alpha)=sin alpha.) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.
3. Высота ромба через диагонали
Выведем формулу вычисления высоты ромба через диагонали. Плошадь ромба через диагонали вычисляется формулой (см. статью Площадь ромба):
а через сторону и высоту, формулой
Из формул (3) и (4) следует:
Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).
Применим к прямоугольному треугольнику AOB теорему Пифагора:
Откуда:
Подставим (7) в (5) и найдем h:
4. Высота ромба через угол и противолежащую диагональ
Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления высоты ромба.
Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Применим теорему синусов для прямоугольного треугольника AOB:
Откуда получим:
С другой стороны (см. параграф 2):
Подставим (9) в (10):
Применяя формулу двойного угла для (small sin alpha, ) имеем: (small sin alpha=2 cdot sin frac{alpha}{2} cdot cos frac{alpha}{2} . ) Подставляя это равенство в формулу (11), получим формулу высоты ромба через угол и противолежащую диагональ:
5. Высота ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.
Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Для прямоугольного треугольника AOB, имеем:
Учитывая, что ( small BO=frac{large d}{large 2}) и ( small angle ABO=frac{large alpha}{large 2}), формулу (13) можно записать так:
или
Подставим (14) в (2):
или, учитывая что (small sin alpha=2 cdot sin frac{alpha}{2} cdot cos frac{alpha}{2} , ) получим:
6. Высота ромба через радиус вписанной в ромб окружности
Покажем, что высота ромба через радиус вписанной окружности вычисляется по формуле:
В статье Площадь ромба показали, что площадь ромба через сторону и высоту вычисляется формулой
а площадь ромба через сторону и радиус вписанной окружности − формулой:
Тогда из формул (16) и (17) следует:
или:
Как найти высоту ромба, если известны диагонали?
Зная диагонали, найти высоту ромба легко. В этом нам поможет теорема Пифагора. И хоть она касается прямоугольных треугольников, в ромбе они тоже есть – их образует пересечение двух диагоналей d1 и d2:
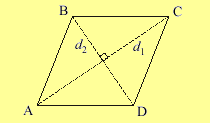
Вообразим, что диагональ 1 равна 30 сантиметрам, а диагональ 2 – 40 см.
Чтобы вычислить высоту, нам придется посчитать площадь ромба и размер одного катета (в ромбе, как известно, они одинаковые).
Итак, наши действия:
Подсчитываем величину стороны по теореме Пифагора. Сторона BC – это гипотенуза (потому что лежит напротив тупого угла) треугольника BXD (X – это пересечение диагоналей d1 и d2). А значит размер этой стороны в квадрате равен сумме квадратов сторон BX и XC. Их размер нам тоже известен (диагонали ромба пересечением делятся пополам) – это 20 и 15 сантиметров. Выходит, что длина стороны BC равняется корню от 20 в квадрате и 15 в квадрате. Сумма квадратов диагоналей равняется 625, а если извлечь это число из корня, получаем размер катета, равный 25 сантиметрам.
Вычисляем площадь ромба при помощи двух диагоналей. Для этого умножаем d1 на d2 и делим результат на 2. Получается: 30 умножить на 40 (= 1200) и поделить на 2 – выходит 600 см кв. – это и есть площадь ромба.
Теперь вычисляем высоту, зная длину стороны и площадь ромба. Для этого нужно площадь поделить на длину катета (это и есть формула вычисления высоты ромба): 1200 делим на 25 – выходит 48 сантиметров. Это окончательный ответ.
Как найти высоту ромба, если известна площадь и периметр (какая формула)?
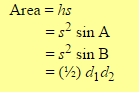
Ознакомьтесь со всеми формулами расчета площади ромба:
Чтобы узнать высоту, нам нужна самая первая формула (Площадь = Высота умножить на Длину стороны).
Допустим, что периметр равен 124 см, а площадь – 155 см кв.
Нам играет на руку то, что у ромба все стороны одинаковые, потому его периметр – это 4 умножить на длину одного катета.
Чтобы подсчитать высоту ромба, нужно узнать размер катета. Вот какие действия помогут в решение задачи:
- Найдем длину стороны ромба через известный периметр. Для этого значение периметра (124) делим на 4, и получаем значение 31 сантиметр – длина катета.
- Подсчитываем высоту через формулу площади. Делим площадь (155 см кв.) на размер катета (31 см) и получаем 5 сантиметров – это размер высоты данной геометрической фигуры.
Как найти высоту ромба, если известна сторона и угол?
Задача кажется сложной, но это не так. Представим, что размер катета ромба равен корню из трех, а угол – 90 градусам.
Чтобы посчитать размер высоты, используем формулу площади ромба (сторона в квадрате умножить на синус угла). Чтобы узнать синус любого градуса, воспользуйтесь таблицей в моем ответе. Синус 90 градусов равняется 1, потому найти высоту будет очень просто. Получается, что площадь равна квадрату длины стороны (3) умножить на синус 90 гр. (1), что в итоге дает ответ- 3 см кв.
А потом делим полученную площадь на размер катета: 3 поделить на корень из 3, и получаем высоту ромба – √3.
Как посчитать высоту ромба, если известна сторона и диагональ?
В этой задаче нужно использовать прямоугольный треугольник, который образован пересечением диагоналей.
Допустим, что сторона равна 10 см, а диагональ – 12 см.
Наши действия:
Находим размер половины второй диагонали при помощи теоремы Пифагора. Гипотенуза в нашем случае – это сторона, потому величина половины диагонали будет равна разнице квадрата катета (10 в квадрате) и квадрата половины известной диагонали (6 в квадрате). Выходит, что нужно от 100 отнять 36 – имеем 64 сантиметра. Добываем корень из этого числа и получаем длину половины второй диагонали – 8 см. А полная длина равна 16 сантиметрам.
Подсчитываем площадь ромба при помощи двух диагоналей. Умножаем длину первой диагонали (12 см) на длину второй (16 см) и делим это на 2 – получаем 96 см кв. (это площадь ромба).
Вычисляем высоту, зная размер стороны и площадь. Для этого 96 поделите на 10 – выходит 9,6 сантиметров – это окончательный ответ.
Рекомендую еще почитать о способах подсчета площади ромба.
Содержание:
- Формулы площади ромба:
- Формула периметра ромба:
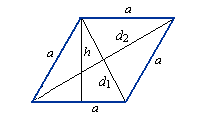
Ромб – это четырёхугольник, у которого все стороны равны.
Ромб можно рассматривать как частный случай параллелограмма, у которого или две смежные стороны равны, или диагонали
взаимно перпендикулярны, или диагональ делит угол пополам. Ромб с прямыми углами называется квадратом.
Формулы площади ромба:
Площадь геометрической фигуры – часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади ромба выражается числом заключающихся в него квадратных единиц.
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
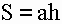
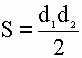
S – площадь ромба
a – длина основания ромба
h – длина высоты ромба
d1 – длина 1-ой диагонали
d2 – длина 2-ой диагонали
См. также: Программа для расчета площади ромба.
Формула периметра ромба:
Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры.
Периметр имеет ту же размерность величин, что и длина.
1) Периметр ромба равен сумме 4-х длин его сторон или произведению
длины любой его стороны на четыре (так как у ромба длины всех сторон равны).
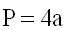
P – периметр ромба
a – длина стороны ромба
Остались вопросы?
Здесь вы найдете ответы.
Что понимается под высотой ромба?
Высота ромба представляет собой перпендикуляр, который опущен из одного из
его углов на сторону, противоположную данному углу.
Высота ромба, опущенная из одного его угла, делит противолежащую сторону
пополам. Как найти величины углов этого ромба?
Обозначим имеющийся ромб как ABCD. Из его угла В проведем высоту ВН, после
чего получим треугольник АВН с прямым углом. Известно, что длина всех
сторон ромба одинаковая, а длина АН равна половине длины АВ. Зная это и
используя теорему, которая является обратной теореме о 30-градусном угле,
можно провести доказательство того, что угол АВН равен 30 градусам.
Учитывая то, что сумма всех углов треугольника равна 180 градусом, можно
найти неизвестную величину третьего угла треугольника:
BAH=180-30-90=60 градусов.
Так, угол АВС равен:
ABC=180-60=120 градусов.
Как найти высоту ромба, если единственной величиной, которая известна,
является длина одной его стороны?
Известна формула площади (S) ромба, которая представляет собой
произведение длины его стороны (а) на высоту (h), проведенную к ней:
S = a*h.
Есть возможность выразить высоту из приведенной выше формулы. Она будет
равна отношению площади ромба к длине его стороны:
h = S/a.
Имеется треугольник с прямым углом и катетами длиной 3 см. и 4 см. Его
площадь аналогична площади ромба со стороной 5 см. Как найти высоту ромба?
Площадь (S) треугольника с прямым углом рассчитывается путем деления
пополам произведения длин его катетов. В данном случае она будет равна:
SΔ = 4*3/2 = 6 см.кв.
Площадь ромба определяется умножением длины его стороны на высоту,
проведенную к ней. Если принять высоту за х, и учесть, что площадь ромба
равна площади прямоугольного треугольника (6 см.кв.), то:
S = 5*x = 6 см.кв.
Отсюда можно найти значение х:
х = 6/5 = 1,2 см.
Ответ: высота ромба составляет 1,2 см.
Как найти высоту ромба при условии, что длины его диагоналей равны 6 см. и 8
см.?
Диагонали, проведенные в ромбе, делят эту фигуру на четыре треугольника,
которые являются равными. Длины катетов этих треугольников составляют 3
см. и 4 см. Такой вывод можно сделать на основании того, что в точке
пересечения диагоналей они делятся пополам. Гипотенуза (с) треугольников
представляет собой сторону ромба. Ее длина равна:
с = √(9+16) = √25 = 5 см.
Следовательно, сторона ромба также равна 5 см.
Площадь ромба высчитывается как произведение длин его диагоналей, деленное
пополам:
S = d1*d2/2 = 6*8/2 = 24 см. кв.
Известна также другая формула, используемая для вычисления площади ромба,
в которой длина его стороны (а) умножается на высоту(h):
S = a*h
Из данной формулы выражаем высоту:
h = S/a = 24/5 = 4,8 см.
Ответ: Высота ромба составляет 4,8 см.
Как найти высоту ромба при условии, что его диагонали равны d1 и d2, а длина
стороны – а?
Высоту ромба можно рассчитать, если его диагонали (d1 и d2)и сторона (а) –
известные величинами. В этом случае для определения неизвестной высоты
следует пользоваться приведенной ниже формулой:
h = (d1 * d2)/a
Площадь ромба составляет 60 см.кв., а его периметр равен 48 см. Как найти
высоту ромба в конкретном случае?
Периметр (Р) ромба равен сумме длин всех его сторон (а) и вычисляется по
следующей формуле:
Р = а+а+а+а
В данном случае периметр ромба равен 48 см., это значит, что:
а+а+а+а = 48 см.
Находим значение а:
а = 48/4 = 12 см.
Площадь ромба (S) является произведением длины его стороны (а) и высоты
(h), проведенной к этой стороне:
S = а*h
В задании сказано, что площадь ромба – 60 см.кв. Значит:
а*h=60
Находим неизвестную высоту:
h=60/а=60/12=5 см.
Ответ: Высота ромба – 5 см.
Как найти высоту ромба, зная о том, что его площадь составляет 48 см.кв., а
периметр – 32 см.?
Согласно формуле расчета периметра (Р) ромба, он равен сумме длин всех его
сторон (а) (Р=а+а+а+а). Известно, что все стороны ромба имеет одинаковую
длину. Из этого следует, что длина одной стороны будет равна ¼ части его
периметра:
а = Р/4 = 32/4 = 8 см.
Площадь (S) ромба можно высчитать путем умножения длины его стороны (а) на
высоту (h), проведенную к ней:
S = а* h
В конкретном случае:
48 = 8* h
Отсюда можем найти высоту (h), разделив площадь на длину стороны ромба:
H = 48/8 = 6 см.
Ответ: Высота ромба составляет 6 см.
Отношение длин диагоналей ромба выглядит как 10/24. Его периметр равен 52
см. Как найти высоту ромба в данном случае?
Периметр (Р) ромба равен сумме длин всех его сторон (а), длины которых
равны. Это значит:
Р = 4*а
По условию задачи:
52 = 4*а
Следовательно:
а = 52/13 = 13 см.
Предположим, что длина одной из диагоналей ромба равна 10х, тогда длина
второй его диагонали будет выглядеть как 24х. Отношение их длин можно
записать в следующем виде:
10х:24х=10:24
Доказано, что диагонали ромба взаимно перпендикулярны и в точке
пересечения они делятся пополам, при этом образуя четыре равных
треугольника с прямым углом.
Теорема Пифагора гласит, что сумма длин его катетов, возведенных во вторую
степень, равна длине гипотенузы, которая также возведена в квадрат:
с2 = а2 + b2
Для данной задачи это равенство записывается так:
(5х)²+(12х)²=13²
Отсюда видно, что:
169х²=169; следовательно, х2 = 1. Значит х тоже будет равен 1.
Длина диаметра, обозначенного как 10х, равна 10 см. (10*1), а длина
второго диаметра, который обозначен как 24х, равна 24 см. (24*1).
Площадь (S) ромба рассчитывается как:
S = d₁*d₂/2 или a·h
Из этого можно составить следующее уравнение:
d₁*d₂=2a*h
Выражаем h и получаем:
h= d₁*d₂/2*а=10·24:26=240/26=120/13 см.
Какая формула используется с целью вычисления высоты ромба?
Ромб имеет четыре высоты. Все они имеют равные длины. Вывод об этом можно
сделать, рассмотрев все треугольные фигуры, элементами которых являются
эти высоты. Есть возожность высчитать высоту ромба при помощи различных
параметров, которые могут быть указаны в условии конкретной задачи.
Предположим, что нам известна площадь (S) ромба и длина его стороны (а). В
этом случае высота ромба будет равна отношению его площади к длине высоты:
h = S/a.
Если же по условию задачи известны длины диагоналей ромба d1 и d2, а также
его сторона а, то высоту можно рассчитать так: h = (d1*d2 )/a.
В случае, когда известна длина стороны (а) ромба и угол А, находящийся
между смежными сторонами, то для расчета высоты ромба используется
следующая формула:
h = a*a*sin A /a = a*sin A.
Существуют также и другие варианты вычисления длины высоты ромба на
основании того, какие величины будут известны по условию задания. Однако
ключевыми параметрами, используя которые можно вычислить высоту ромба,
являются диагонали, длина любой его стороны и угол, образованный между
смежными сторонами.
В каком виде записываются формулы, используемые для определения площади
ромба?
Площадь ромба можно рассчитать одним из трех способов:
1. S = a² sin a, в которой α — образованный двумя сторонами угол, a —
сторона.
2. S = ah, или Длина стороны ромба, умноженная на его высоту.
3. S = (d1*d2)/2, в которой d1 и d2 – длины диагоналей фигуры.
На сторону ромба опущена высота, которая на 1,7 см. меньше ее длины.
Периметр фигуры составляет 32 см. Как в данном случае вычислить площадь
ромба?
Зная, чему равен периметр ромба, можно вычислить длину его стороны:
Р/4 = 8 см.
Известно, что высота данной фигуры меньше ее стороны на 1,7 см. Теперь
можем определить длину высоты:
h = 8-1,7 = 6,3 см.
Площадь ромба можно найти, умножив его сторону на высоту, которая на нее
опущена:
8 * 6,3 = 50,4 см².кв.
Ответ: S = 50,4 см. кв.
Известно, что диагонали ромба относятся как 4/3, а его сторона составляет 10
см. Как найти площадь ромба?
Если длины диагоналей фигуры относятся как 4/3, то их половины будут
относиться также:
(4d)²+(3d)²=10² = 16d²+9d² = 100
Отсюда:
25d²=100
d =2,
Значит:
d¹/2 = 4d = 8 см.
d²/2 = 3d = 6 см.
Теперь можно найти площадь:
S= 2*d¹/2*d²/2=2*8*6 = 96 см.кв.
Ответ: S ромба = 96 см.кв.
Как записывается формула расчета площади ромба через длины его диагоналей d1
и d2?
Площадь ромба можно описать как сумму площадей 2-х треугольных фигур,
основанием которых является одна диагональ, а вторая диагональ ромба
представляет собой сумму длин высот этих фигур. Диагонали ромба при
пересечении образуют угол в 90 градусов. На основании этого можно найти
площадь ромба следующим образом:
S = ½ d1*d2.
Как записать формулу вычисления площади ромба через диагонали?
Известно, что, пересекаясь, диагонали ромба образуют угол в 90 градусов и
в точке пересечения делятся пополам.
Для расчета площади ромба через диагонали нужно перемножить их длины, а
затем разделить полученное число на два:
S = ½ d1*d2.
Для примера можно рассмотреть ромб, одна диагональ которого равна 5 см., а
вторая – 4 см. Тогда его площадь будет равна:
S=1/2*5*4=10 см. кв.
Как выглядит формула для определения площади ромба?
S ромба возможно вычислить, перемножив длину одной из его сторон (а) и
высоту (h). Формула записывается так:
S=a*h.
См. также: Программа для расчета периметра ромба.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Информация по назначению калькулятора
Ромб – это четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу. Все ромбы являются параллелограммами, но не все параллелограммы являются ромбами. Все квадраты являются ромбами, но не все ромбы являются квадратами. Противоположные внутренние углы ромбов совпадают. Диагонали ромба всегда делят пополам друг друга под прямым углом.
Четыре внутренних угла ромба всегда составляют в сумме 360°, а его диагонали всегда перпендикулярны друг другу
Одной из двух характеристик, которые делают ромб уникальным, является то, что его четыре стороны равны по длине или конгруэнтны. Другое идентифицирующее свойство состоит в том, что противоположные стороны параллельны.
Онлайн калькулятор предназначен для нахождения параметров ромба, таких как:
- Длины сторон
- Высота
- Периметр
- Площадь
- Диагонали
- Углы
- Радиус Вписанной окружности
- Диаметр Вписанной окружности
- Длина Вписанной окружности
- Площадь Вписанной окружности
– равны между собой (AB=BC=CD=DA)
– что бы найти высоту ромба, необходимо его площадь поделить на сторону (h=S/AB)
– равен сумме всех сторон, или стороне ромба умноженной на 4 (P=AB+BC+CD+DA=AB*4)
– равна произведению стороны и высоты (S=AB*h)
– всегда перпендикулярны
– всегда составляют в сумме 360°
