Как найти высоту ромба с рисунком

Здравствуйте, уважаемые читатели. В этой статье продолжим разбор задач из 23 задания ОГЭ по математике.

Задача

Высота AH ромба ABCD делит сторону CD на отрезки DH = 15 и CH = 2. Найдите высоту ромба.

К задаче построим рисунок и напишем условие

Решение

1) Так как ABCD ромб, то все стороны равны. Найдем CD

2) Рассмотрим треугольник AHD – прямоугольны. По теореме Пифагора найдем AH

Ответ 8

Вам понравился материал? Поблагодарить легко! Будем весьма признательны, если поделитесь этой статьей в социальных сетях, поставите лайк и подпишитесь на мой блог

Высота ромба онлайн

1. Высота ромба через сторону и площадь

Пусть задан ромб (Рис.1).

Формула площади ромба через сторону и высоту имеет следующий вид:

Откуда легко вывести формулу высоты ромба через сторону и площадь:

2. Высота ромба через сторону и угол

Рассмотрим ромб со стороной a и углом α между сторонами (Рис.2). Выведем формулу вычисления высоты ромба через сторону и угол.

Проведем высоту AH. Для прямоугольного треугольника AHB применим теорему синусов:

Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:

Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого угла. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: (small angle C=180°-alpha.) Следовательно (small sin angle C=sin(180°-alpha)=sin alpha.) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.

3. Высота ромба через диагонали

Выведем формулу вычисления высоты ромба через диагонали. Плошадь ромба через диагонали вычисляется формулой (см. статью Площадь ромба):

а через сторону и высоту, формулой

Из формул (3) и (4) следует:

Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).

Применим к прямоугольному треугольнику AOB теорему Пифагора:

Откуда:

Подставим (7) в (5) и найдем h:

4. Высота ромба через угол и противолежащую диагональ

Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления высоты ромба.

Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Применим теорему синусов для прямоугольного треугольника AOB:

Откуда получим:

С другой стороны (см. параграф 2):

Подставим (9) в (10):

Применяя формулу двойного угла для (small sin alpha, ) имеем: (small sin alpha=2 cdot sin frac{alpha}{2} cdot cos frac{alpha}{2} . ) Подставляя это равенство в формулу (11), получим формулу высоты ромба через угол и противолежащую диагональ:

5. Высота ромба через угол и диагональ из данного угла

Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.

Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Для прямоугольного треугольника AOB, имеем:

Учитывая, что ( small BO=frac{large d}{large 2}) и ( small angle ABO=frac{large alpha}{large 2}), формулу (13) можно записать так:

или

Подставим (14) в (2):

или, учитывая что (small sin alpha=2 cdot sin frac{alpha}{2} cdot cos frac{alpha}{2} , ) получим:

6. Высота ромба через радиус вписанной в ромб окружности

Покажем, что высота ромба через радиус вписанной окружности вычисляется по формуле:

В статье Площадь ромба показали, что площадь ромба через сторону и высоту вычисляется формулой

а площадь ромба через сторону и радиус вписанной окружности − формулой:

Тогда из формул (16) и (17) следует:

или:

Для получения максимального балла задание нужно оформлять разборчивым почерком с подробным решением. Обязательно должны присутствовать чертёж, дано и решение.

Высота ромба онлайн

С помощю этого онлайн калькулятора ромба можно найти высоту ромба по известным элементам. Для нахождения высоты ромба введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.

Открыть онлайн калькулятор

1. Высота ромба через сторону и площадь

Пусть задан ромб (Рис.1).

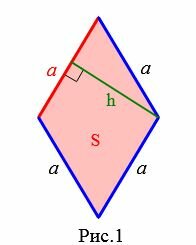
Формула площади ромба через сторону и высоту имеет следующий вид:

Откуда легко вывести формулу высоты ромба через сторону и площадь:

(small h=frac<large S><large a>.)

2. Высота ромба через сторону и угол

Рассмотрим ромб со стороной a и углом α между сторонами (Рис.2). Выведем формулу вычисления высоты ромба через сторону и угол.

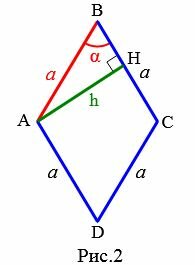
Проведем высоту AH. Для прямоугольного треугольника AHB применим теорему синусов:

(small frac<large a><large sin 90°>=frac<large h><large sin alpha>.)

(1)

Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:

(small h=a cdot sin alpha.)

(2)

Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого угла. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: (small angle C=180°-alpha.) Следовательно (small sin angle C=sin(180°-alpha)=sin alpha.) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.

3. Высота ромба через диагонали

Выведем формулу вычисления высоты ромба через диагонали. Плошадь ромба через диагонали вычисляется формулой (см. статью Площадь ромба):

(small S= frac<large d_1d_2><large 2>,)

(3)

а через сторону и высоту, формулой

(small S= a cdot h.)

(4)

Из формул (3) и (4) следует:

(small frac<large d_1d_2><large 2>=a cdot h.)

(5)

Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).

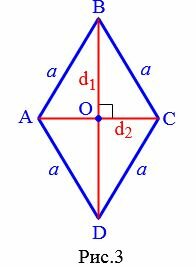
Применим к прямоугольному треугольнику AOB теорему Пифагора:

(small a^2= left( frac<large d_1> <large 2>right)^2+left( frac<large d_2> <large 2>right)^2.)

(6)

(small a= frac<sqrt<large d_1^2+d_2^2>> <large 2>)

(7)

Подставим (7) в (5) и найдем h:

(small frac<large d_1d_2><large 2>=frac<sqrt<large d_1^2+d_2^2>> <large 2>cdot h,)

(small h= frac<large d_1d_2> <sqrt<large d_1^2+d_2^2>>.)

(8)

4. Высота ромба через угол и противолежащую диагональ

Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления высоты ромба.

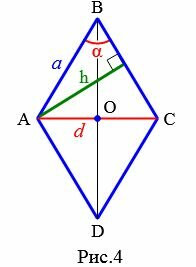
Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Применим теорему синусов для прямоугольного треугольника AOB:

(small a=frac<large d><large 2 cdot sin frac< alpha>< 2>>.)

(9)

С другой стороны (см. параграф 2):

(small h=a cdot sin alpha.)

(10)

Подставим (9) в (10):

(small h=frac<large d cdot sin alpha><large 2 cdot sin frac<large alpha><large 2>>.)

(11)

Применяя формулу двойного угла для (small sin alpha, ) имеем: (small sin alpha=2 cdot sin frac<alpha> <2>cdot cos frac<alpha> <2>. ) Подставляя это равенство в формулу (11), получим формулу высоты ромба через угол и противолежащую диагональ:

(small h=d cdot cos frac<large alpha><large 2>.)

(12)

5. Высота ромба через угол и диагональ из данного угла

Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.

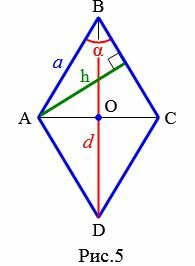
Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Для прямоугольного треугольника AOB, имеем:

(small frac<large OB > <large a>=cos angle ABO.)

(13)

Учитывая, что ( small BO=frac<large d><large 2>) и ( small angle ABO=frac<large alpha><large 2>), формулу (13) можно записать так:

(small frac< large frac<large d > <large 2>><large a>= cos frac<large alpha> <large 2>.)

(small a=frac<large d><large 2 cdot cos large frac< alpha>< 2>>.)

(14)

Подставим (14) в (2):

(small h= frac<large d cdot sin alpha ><large 2 cdot cos frac<large alpha><large 2>> .)

или, учитывая что (small sin alpha=2 cdot sin frac<alpha> <2>cdot cos frac<alpha> <2>, ) получим:

(small h= d cdot sin frac<large alpha><large 2>.)

(15)

6. Высота ромба через радиус вписанной в ромб окружности

Покажем, что высота ромба через радиус вписанной окружности вычисляется по формуле:

В статье Площадь ромба показали, что площадь ромба через сторону и высоту вычисляется формулой

(small S= a cdot h.)

(16)

а площадь ромба через сторону и радиус вписанной окружности − формулой:

Ромб. Свойства и признаки ромба

Ромб – это параллелограмм, у которого все стороны равны.

Если у ромба – прямые углы, то он называется квадратом.

Свойства ромба

1. Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.

Помимо этого:

2. Диагонали ромба перпендикулярны.

3. Диагонали ромба являются биссектрисами его углов.

4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.

Признаки ромба

Чтобы параллелограмм оказался ромбом, необходимо выполнение одного из следующих условий:

1. Все стороны параллелограмма равны между собой ().

2. Диагонали пересекаются под прямым углом ().

3. Диагонали параллелограмма являются биссектрисами его углов.

Площадь ромба

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Ромб. Формулы, признаки и свойства ромба

Признаки ромба

∠BAC = ∠CAD или ∠BDA = ∠BDC

Δ ABO = Δ BCO = Δ CDO = Δ ADO

Основные свойства ромба

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

AC 2 + BD 2 = 4AB 2

Сторона ромба

Формулы определения длины стороны ромба:

1. Формула стороны ромба через площадь и высоту:

2. Формула стороны ромба через площадь и синус угла:

3. Формула стороны ромба через площадь и радиус вписанной окружности:

4. Формула стороны ромба через две диагонали:

5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):

6. Формула стороны ромба через большую диагональ и половинный угол:

7. Формула стороны ромба через малую диагональ и половинный угол:

8. Формула стороны ромба через периметр:

Диагонали ромба

Формулы определения длины диагонали ромба:

d ₁ = a √ 2 + 2 · cosα

d ₁ = a √ 2 – 2 · cosβ

d ₂ = a √ 2 + 2 · cosβ

d ₂ = a √ 2 – 2 · cosα

d ₁ = 2 a · cos ( α /2)

d ₁ = 2 a · sin ( β /2)

d ₂ = 2 a · sin ( α /2)

d ₂ = 2 a · cos ( β /2)

7. Формулы диагоналей через площадь и другую диагональ:

8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:

Периметр ромба

Периметром ромба называется сумма длин всех сторон ромба.

Длину стороны ромба можно найти за формулами указанными выше.

Формула определения длины периметра ромба:

Площадь ромба

Формулы определения площади ромба:

4. Формула площади ромба через две диагонали:

5. Формула площади ромба через синус угла и радиус вписанной окружности:

6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):

S =	1	d 1 2 · tg ( α /2)
2

S =	1	d 2 2 · tg ( β /2)
2

Окружность вписанная в ромб

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

6. Формула радиуса круга вписанного в ромб через две диагонали:

r =	d 1 · d 2
2√ d 1 2 + d 2 2

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

[spoiler title=”источники:”]

http://ru.onlinemschool.com/math/formula/rhombus/

[/spoiler]

Всего: 40    1–20 | 21–40

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 40    1–20 | 21–40