В курсовом проекте
необходимо назначить высоту главной
балки большого
![]() и малого
и малого![]() пролётов.
пролётов.
Главная балка
может рассчитываться на прочность как
в пределах упругих деформаций, так и с
учётом развития пластических деформаций.
Максимальная
высота балки определяется исходя из
заданной высоты перекрытия
![]() и его конструкции. При поэтажном
и его конструкции. При поэтажном
сопряжении балок:
![]() ,
,
(6.3)
где
![]() – толщина настила;
– толщина настила;
![]() – высота балки
– высота балки
настила;
![]() – высота вспомогательной
– высота вспомогательной
балки;
![]() (табл. Е.1 [2]) –
(табл. Е.1 [2]) –
отношение пролёта главной балки к её
предельному прогибу.
Минимальная высота
балки рассчитывается из условия
обеспечения жёсткости при полном
использовании расчётного сопротивления
стали:
![]() .
.
(6.4)
Для первоначальных
прикидок оптимальная высота сварной
балки переменного сечения вычисляется
по формуле
![]() ,
,
(6.5)
где
![]() – требуемый момент сопротивления сечения
– требуемый момент сопротивления сечения
балки:
![]() .
.
(6.6)
Задавшись толщиной
стенки
![]() по табл. 2 с учётом сортамента на листовую
по табл. 2 с учётом сортамента на листовую
сталь (прил. табл. 1), уточняется значение
оптимальной высоты балки:
![]() ,
,
(6.7)
где
![]() – коэффициент, зависящий от конструктивного
– коэффициент, зависящий от конструктивного
оформления балки, принимаемый для
сварных балок равным 1,15…1,2.
В случае, если
![]() ,
,
рекомендуется снизить расчётное
сопротивление материала, приняв менее
прочную сталь.
Окончательно
высота балки
![]() назначается близкой к оптимальной
назначается близкой к оптимальной![]() и кратной 100мм
и кратной 100мм
при соблюдении условия
![]() .
.
Таблица 2
Рекомендуемые
соотношения высоты балки и толщины
стенки
|
|
1 |
1,5 |
2 |
3 |
4 |
5 |
|
|
8…10 |
10…12 |
12…14 |
16…18 |
20…22 |
22…24 |
6.3. Подбор сечения балки
В курсовом проекте
требуется рассчитать и законструировать
только главную балку пролета
![]() .
.
Минимальная
толщина стенки
![]() определяется из условия работы её на
определяется из условия работы её на
касательные напряжения на опоре по
формуле
![]() ,
,
(6.8)
где
![]() – при работе на срез только стенки (без
– при работе на срез только стенки (без
учета поясов).
Для балок высотой
1…2 м
рациональное значение толщины стенки
определяется по эмпирической формуле,
мм:
![]() ,
,
(6.9)
где
![]() – высота главной балки,мм.
– высота главной балки,мм.
Если назначенная
в п. 6.2 толщина стенки отличается от
полученных по формулам (6.8) и (6.9) более
чем на 2 мм,
необходимо принять новое её значение
(![]() ),
),
затем вновь вычислить оптимальную
высоту балки![]() и скорректировать её высоту
и скорректировать её высоту![]() .
.
После назначения
толщины стенки определяются размеры
горизонтальных поясных листов, исходя
из необходимой несущей способности и
жёсткости балки. Для этого вычисляется
требуемый момент инерции сечения балки
![]() .
.
Находится момент
инерции стенки балки
![]() ,
,
где
![]() – высота стенки балки, предварительно
– высота стенки балки, предварительно
принимаемая![]()
см.
Тогда момент
инерции, приходящийся на поясные листы,
будет равен
![]() .
.
Определяется
требуемая площадь сечения одного
поясного листа
![]() ,
,
где
![]()
см – расстояние
между центрами тяжести поясов.
Задавшись по
сортаменту (прил. табл. 1) толщиной пояса
![]()
(![]() ),
),
находится его требуемая ширина![]() .
.
При назначении
ширины пояса
![]() необходимо учитывать следующие
необходимо учитывать следующие
рекомендации:
а) из условия
обеспечения общей устойчивости балки
![]() ;
;
б) по конструктивным
соображениям
![]() мм;
мм;
в) по расчёту
![]() ;
;
г) из условия
равномерного распределения напряжений
по ширине пояса
![]() ;
;
д )
)
из условия обеспечения местной
устойчивости пояса
![]() .
.
Ширина пояса
принимается с учётом стандартной ширины
листов универсальной стали в соответствии
с сортаментом (прил. табл. 1).
После назначения
размеров поясов и стенки определяются
геометрические характеристики сечения
(рис. 3):
– площадь пояса
![]() ;
;
–
Рис.
3. Сечение балки
площадь стенки![]() ,
,
где![]() ;
;
– момент инерции
стенки
![]() ;
;
– момент инерции
балки
![]() ,
,
где![]() ;
;
– момент сопротивления
![]() .
.
производится
проверка прочности принятого сечения:
![]() .
.
(6.10)
Недонапряжение,
определяемое по формуле
![]() ,
,
должно составлять
не более
![]() .
.
Соседние файлы в папке металконструкции
- #
- #
26.03.2015760.9 Кб37МК КП-1(студентам).dwg
3.6. Расчет и конструирование составной сварной главной балки
Применяют сечение главной балки двутавровое симметричное, сваренное из трех металлопрокатных листов, так как прокатные балки из-за ограниченности размеров профиля не могут удовлетворить требования по несущей способности и жесткости (большой пролет и значительные нагрузки на балку).
Пример 3.4. Подобрать сечение составной сварной главной балки пролетом l = 18 м. Шаг балок b в составе балочной клетки нормального типа равен шагу колонн B = 6 м (рис. 3.7). Шаг балок настила 3 м, вес балок настила из I40 gn,бн = 0,19 кН/м2. Настил железобетонный толщиной 12 см, весом 30 кН/м2 под полезную нагрузку pn = 12,55 кН/м2. Коэффициент надежности по нагрузке для железобетонного настила γfgb = 1,1. Сталь для климатического района строительства II4 C255 c расчетным сопротивлением Ry = 24 кН/см2 для листового и фасонного проката толщиной до 20 мм включительно и Ry = 23 кН/см2 для проката толщиной свыше 20 мм.

Рис. 3.7. Балочная клетка с железобетонным настилом
3.6.1. Определение усилий
При частом расположении балок настила (а1 = 3 м) < (l/5 = 18/5 = 3,6 м) сосредоточенную нагрузку, передаваемую на главную балку от балок настила, заменяют равномерно распределенной нагрузкой, собираемой с соответствующей грузовой площади (см. рис. 3.4).
Расчетная схема главной балки представлена на рис. 3.8.
Нормативная нагрузка
Рекомендуемые материалы

Расчетная нагрузка

Расчетный изгибающий момент в середине пролета

Нормативный изгибающий момент
Mn,max = αqnl2/8 = 1,04 · 94,44 · 182 / 8 = 3824,82 кН∙м.

Рис. 3.8. Расчетная схема главной балки
Расчетная поперечная сила в опорном сечении

где a = 1,04 – коэффициент, учитывающий собственный вес главной балки (предварительно принимается a = 1,02 – 1,05).
3.6.2. Компоновка сечения
Балку рассчитываем в упругой стадии работы (рис. 3.9).

Рис. 3.9. Сечение главной балки и эпюры напряжений σ и τ
Из условия прочности требуемый момент сопротивления балки

где Ry = 23 кН/см2 при толщине проката более 20 мм.
Назначаем высоту сечения балки h, которая определяется максимально допустимым прогибом балки, экономическими соображениями и строительными габаритами площадки.
Наименьшая рекомендуемая высота балки hmin определяется из условия жесткости балки (второе предельное состояние) при равномерно распределенной по длине балки нагрузке:

где qn – суммарная погонная нормативная нагрузка на балку.
Минимальная высота балки

где fu = 7,4 см – предельный прогиб главной балки пролетом l = 18 м, определенный интерполяцией по табл. 1.4.
Высоту разрезной главной балки принимают в пределах (1/10 – 1/13)l =
= (1,8 – 1,4 м). Предварительно принимаем высоту балки h = 1,5 м.
Оптимальная высота балки по металлоемкости

где tw –толщина стенки балки, определяемая по эмпирической зависимости: tw = 7 + 3h/1000 = 7 + 3 · 1500 / 1000 = 11,5 мм.
Принимаем tw = 12 мм.
Допускается отклонение оптимальной высоты балки в меньшую или большую сторону на 10 – 15%, так как это мало отражается на весе балки.
Максимально возможная высота балки определяется строительной высотой перекрытия H (разницей в отметках верха настила рабочей площадки и верха габарита помещения, расположенного под площадкой) и зависит от сопряжения балок между собой по высоте.
Сопряжение балок может быть поэтажное, в одном уровне и пониженное (рис. 3.10).
При поэтажном сопряжении балки, непосредственно поддерживающие настил, укладывают на главные или вспомогательные балки сверху. Это наиболее простой и удобный в монтажном отношении способ сопряжения балок, но он требует большой строительной высоты. Чтобы увеличить высоту главной балки, необходимо применять сопряжение балок в одном уровне, при котором верхние полки балок настила и главных балок располагаются на одной отметке.

Рис. 3.10. Сопряжения балок:
а – поэтажное; б – в одном уровне; в – пониженное
Строительная высота балки
hстр = H – (tн + hбн + Δ) = (1300 – 1000) – (12 + 40 + 13) = 235 см,
где Δ = fu + (30 …100 мм) = 7,4 + 5,6 = 13 см – размер, учитывающий пре- дельный прогиб балки fu = 7,4 см и выступающие части, расположенные ниже нижнего пояса балки (стыковые накладки, болты, элементы связей и т.п.);
1300 и 1000 – отметки верха настила и габарита под площадкой.
Таблица 3.7
Сортамент горячекатаных полос по ГОСТ 103-76*
|
Толщина полос, мм |
4; 5; 6; 7; 8; 9; 10; 11; 12; 14; 16; 18; 20; 22; 25; 28; 30; 32; 36; 40 |
|
Ширина полос, мм |
40; 45; 50; 55; 60; 63; 65; 70; 75; 80; 85; 90; 95; 100; 105; 110; 120; 125; 130; 140; 150; 160; 170; 180; 190; 200 |
Высота стенки hw приблизительно равна высоте балки h, ее размеры рекомендуется увязать со стандартными размерами листов, выпускаемых заводами (табл. 3.8 и 3.9). Сравнивая полученные данные, назначаем стенку высотой hw = 1500 мм и толщиной tw = 12 мм (минимальная толщина стенки принимается 8 мм, при отсутствии локальных напряжений ее можно принять 6 мм).
Таблица 3.8
Сталь листовая горячекатаная (выборка из ГОСТ 19903-74*)
|
Ширина, мм |
500; 510; 600; 650; 670; 700; 710; 750; 800; 850; 900; 950; 1000; 1100; 1250; 1400; 1420; 1500 и далее до 3000 мм кратно 100 мм |
|
Толщина, мм |
6; 7; 8; 9; 10; 11; 12; 14; 16; 18; 20; 22; 25; 28; 30; 32; 36; 40 |
Таблица 3.9
Сталь широкополосная универсальная по (по ГОСТ 82-70*)
|
Ширина, мм |
180 (по заказу); 200; 210; 220; 240; 250; 260; 280; 300; 320; 340; 360; 380; 400; 420; 450; 460; 480; 500; 520; 530; 560; 600; 630; 650; 670; 700; 750; 800; 850; 900; 950; 1000; 1050 |
|
Толщина, мм |
6; 7; 8; 9; 10; 11; 12; 14; 16; 18; 20; 22; 25; 28; 30; 32; 36; 40 |
В строительных конструкциях рекомендуется применять листовую сталь толщиной от 6 до 22 мм с градацией 2 мм, далее – по сортаменту.
Толщиной поясов задаются в пределах от 10 до 40 мм, увязывая ее с толщиной стенки: не менее толщины стенки tw и не более 3tw = 36 мм (в поясных швах при приварке толстых поясных листов к тонкой стенке развиваются значительные усадочные растягивающие напряжения). Приняв предварительно толщину поясов tf = 25 мм, назначаем высоту балки h = 1550 мм. При высоте балки менее 1100 мм рекомендуется принимать стенку из широкополосной универсальной стали по ГОСТ 82-70*.
Определяем требуемую толщину стенки из условия прочности на срез в опорном сечении:
tw = kQmax/(hwRsγc) = 1,5 · 1042,3 / (150 · 13,92 · 1) = 0,75 см = 7,5 мм,
что меньше предварительно принятой толщины tw = 12 мм (здесь k = 1,5 – для разрезных балок, опирающихся на колонну с помощью опорного ребра, приваренного к торцу балки). Считается, что в опорном сечении балки на касательные напряжения от поперечной силы работает только стенка. При передаче давления на колонну через опорные ребра, торцы которых совмещаются с осью полок сплошной колонны или стенок ветвей сквозной колонны, включаются в работу и пояса балки, коэффициент принимается k = 1,2.
Если толщина стенки tw будет изменена и принята из условия прочности на срез, при этом будет отличаться на 2 мм и более от предварительно принятой толщины (при определении оптимальной высоты балки), следует произвести перерасчет hopt с вновь принятой толщиной стенки.
Проверяем необходимость постановки продольных ребер жесткости для исключения образования волн выпучивания в верхней сжатой части стенки от нормальных напряжений. Постановка продольных ребер жесткости усложняет конструкцию балки, поэтому они целесообразны только в высоких балках (более двух метров), имеющих тонкую стенку с гибкостью 
Условная гибкость стенки

Оставляем без изменений принятую толщину стенки tw = 12 мм, так как она удовлетворяет условиям прочности на действие касательных напряжений
и не требует укрепления ее продольным ребром жесткости.
Размеры горизонтальных поясных листов находим, исходя из необходимой несущей способности балки. Вычисляем требуемый момент инерции сечения балки:

Находим момент инерции стенки балки:

Момент инерции, приходящийся на поясные листы:

Момент инерции поясных листов балки относительно ее нейтральной оси х-х (пренебрегая моментом инерции поясов относительно собственной оси 1-1 ввиду его малости) можно расписать: If ≈ 2Af(hf/2)2,
где Af – площадь сечения одного пояса;
hf = h – tf = 155 – 2,5 = 152,5 см – расстояние между центрами тяжести поясов.
Находим требуемую площадь одного пояса:

Ширина пояса

Ширина пояса должна отвечать следующим требованиям:
– bf = (1/3 – 1/5)h = 51,7 – 31 см при h = 155 см;
– bf ≥ 180 мм.
По сортаменту принимаем пояса из горячекатаного широкополочного универсального проката по табл. 3.9 сечением 450´25 мм, для которых ширина bf находится в рекомендуемых пределах.
Необходимо проверить местную устойчивость сжатого пояса, для чего отношение свеса пояса  = (450 – 12) / 2 = 219 мм к его толщине tf должно быть не более предельного, определяемого по табл. 3.10.
= (450 – 12) / 2 = 219 мм к его толщине tf должно быть не более предельного, определяемого по табл. 3.10.
Проверяем:

Условие выполняется.
3.6.3. Проверка прочности балки
По назначенным размерам вычисляем фактические характеристики сечения балки:
– момент инерции

– момент сопротивления

– статический момент половины сечения относительно нейтральной оси

– площадь сечения

По найденной площади A и плотности стального проката ρ = 7850 кг/м3 определяем вес 1 м пог. балки:

где k = 1,1 – конструктивный коэффициент, учитывающий увеличение веса балки за счет ребер жесткости, накладок и т.п.
Таблица 3.10
Наибольшие значения отношения ширины свеса сжатого пояса bef
к толщине tf
|
Расчет изгибаемых элементов |
Характеристика свеса |
Наибольшие значения отношения |
|
В пределах упругих деформаций |
Неокаймленный |
|
|
Окаймленный ребром |
|
|
|
С учетом развития пластических деформаций1 |
Неокаймленный |
но не более
|
|
Окаймленный ребром |
но не более
|
1При  наибольшее значение отношения
наибольшее значение отношения  следует принимать:
следует принимать:
для неокаймленного свеса 
для окаймленного ребром свеса 
Обозначения, принятые в табл. 3.10:
hef – расчетная высота стенки;
tw – толщина стенки балки.
Уточняем расчетные значения изгибающего момента M и поперечной силы Q с учетом собственного веса главной балки, для этого определяем:
– нормативную нагрузку
 qn′ = qn + qn,гб = 94,44 + 3,5 = 97,94 кН/м;
qn′ = qn + qn,гб = 94,44 + 3,5 = 97,94 кН/м;
– расчетную нагрузку
 q′ = q + qn,гб γfg = 111,36 + 3,5 ∙ 1,05 = 115,03 кН/м;
q′ = q + qn,гб γfg = 111,36 + 3,5 ∙ 1,05 = 115,03 кН/м;
– расчетный изгибающий момент
Mmax = q′ l2/8 = 115,03 ∙ 182 / 8 = 4658,72 кН·м;
– нормативный изгибающий момент

– поперечную силу
Qmax = q′l/2 = 115,03 · 18/2 = 1033,59 кН.
Проверка прочности балки по нормальным напряжениям:

Недонапряжение в балке составляет

что допустимо в составном сечении согласно СНиП [6].
Проверка прочности балки на срез по касательным напряжениям производится по формуле


Рис. 3.11. Схема распределения сосредоточенной нагрузки
на стенку сварной балки при поэтажном сопряжении балок
При наличии местных напряжений σloc, возникающих в местах приложения сосредоточенной нагрузки к верхнему поясу при поэтажном сопряжении балок (рис. 3.11) (балки настила попадают между поперечными ребрами жесткости, укрепляющими стенку от потери устойчивости), необходима проверка прочности стенки на местные сминающие напряжения по формуле

где σloc = F/(lef tw) = 334,08 / (20,5 · 1,2) = 13,58 кН/см2,
здесь F = 2Q = 2 · 167,04 = 334,08 кН – расчетное значение сосредоточенной силы, равное двум реакциям от балок настила;
 условная длина распределения сосредоточенной нагрузки на стенку главной балки;
условная длина распределения сосредоточенной нагрузки на стенку главной балки;
b = 155 мм – ширина пояса балки настила;
tf = 25 мм – толщина верхнего пояса главной балки.
Прочность балки обеспечена.
3.6.4. Изменение сечения балки по длине
Сечение составной балки, подобранное по максимальному изгибающему моменту в середине пролета, можно уменьшить в местах снижения моментов. Наибольший эффект дает симметричное изменение сечения на расстоянии x = l/6 от опор. Наиболее простым является изменение сечения за счет уменьшения ширины пояса (рис. 3.12).

Рис. 3.12. Изменение сечения балки по длине
Стыкуем сжатый и растянутый пояса прямым сварным швом с выводом концов шва на технологические подкладки с применением механизированной сварки без использования физических способов контроля качества швов. Расчетное сопротивление таких сварных соединений при растяжении принимается пониженным:
Rwy = 0,85Ry = 0,85 ∙ 23 = 19,55 кН/см2.
Для снижения концентрации напряжений при сварке встык элементов разной ширины на элементе большей ширины делаем скосы с уклоном 1:5.
Определяем расчетный момент и перерезывающую силу на расстоянии  от опоры:
от опоры:


Определяем требуемые:
– момент сопротивления измененного сечения, исходя из прочности сварного стыкового шва, работающего на растяжение:

– момент инерции измененного сечения

– момент инерции пояса

– площадь пояса

– ширину пояса

По конструктивным требованиям ширина пояса должна отвечать условиям:
– 
– 
– 
По сортаменту принимаем измененный пояс из универсальной стали сечением 240´25 мм с площадью 
Вычисляем геометрические характеристики измененного сечения балки:
– момент инерции

– момент сопротивления
W1 = 2I1/h = 2∙1035188 / 155 = 13357 см3;
– статический момент пояса относительно оси х-х

Производим проверку прочности балки в месте изменения сечения в краевом участке стенки на уровне поясных швов (рис. 3.13) на наиболее неблагоприятное совместное действие нормальных и касательных напряжений, для чего определяем:
– нормальное напряжение

– касательное напряжение


Рис. 3.13. Распределение напряжений в месте изменения сечения балки
Проверяем прочность стенки балки по формуле

где 1,15– коэффициент, учитывающий локальное развитие пластических де-
формаций в стенке балки.
В случае невыполнения условия необходимо увеличить толщину стенки tw.
При наличии местной нагрузки Fb (см. рис. 3.11) и отсутствия поперечного ребра жесткости в рассматриваемом сечении проверка прочности стенки производится с учетом локальных напряжений σloc по формуле

Если эта проверка не выполняется, то стенку балки под сосредоточенной нагрузкой можно укрепить поперечным ребром жесткости. Это ребро через пригнанный торец воспримет сосредоточенное давление и через сварные швы, соединяющие ребро со стенкой, распределит его на всю высоту стенки. При наличии таких ребер стенка балки с учетом действия местных напряжений на прочность не проверяется.
3.6.5. Проверка общей устойчивости балки
Общая устойчивость балки считается обеспеченной при передаче нагрузки через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный, а также, если соблюдается условие: отношение расчетной длины участка балки lef между связями, препятствующими поперечным смещениям сжатого пояса балки, к его ширине bf не превышает критическое значение, определяемое по формуле

где lef = 3 м – расстояние между точками закрепления сжатого пояса от поперечных смещений, равное шагу балок настила a1.
Проверяем:
– в середине пролета балки

– в измененном сечении балки

Общая устойчивость балки обеспечена.
В случае невыполнения условий необходимо проверить устойчивость балки по формуле

где φb – коэффициент устойчивости при изгибе, определяемый по [6, прил.7*];
Wc – момент сопротивления сечения относительно оси x–x, вычисленный для сжатого пояса;
 gс = 0,95 – коэффициент условий работы при расчетах на общую устойчивость при jb < 1 (см. табл. 1.3).
gс = 0,95 – коэффициент условий работы при расчетах на общую устойчивость при jb < 1 (см. табл. 1.3).
3.6.6. Проверка местной устойчивости элементов балки
Проверка местной устойчивости сжатого пояса не требуется, так как она была обеспечена надлежащим назначением отношения свеса пояса к толщине (см. п. 3.6.2).
Проверка местной устойчивости стенки балки. Под действием нормальных и касательных напряжений стенка балки может потерять местную устойчивость, т.е. может произойти ее местное выпучивание. Это произойдет в том случае, если действующие в балке отдельные виды напряжений или их совместное воздействие превысят критические напряжения потери устойчивости. Устойчивость стенки обычно обеспечивают не за счет увеличения ее толщины, что привело бы к повышенному перерасходу материала из-за большого размера стенки, а за счет укрепления ее ребрами жесткости.
Стенку балки следует укреплять поперечными ребрами жесткости, если значение условной гибкости  превышает 3,2 при отсутствии местной нагрузки на пояс балки и 2,2 – при наличии местной нагрузки.
превышает 3,2 при отсутствии местной нагрузки на пояс балки и 2,2 – при наличии местной нагрузки.
Определяем условную гибкость стенки:

следовательно, поперечные ребра жесткости необходимы (рис. 3.14). Расстояние между основными поперечными ребрами a не должно превышать 2hw при lw > 3,2 и 2,5hw при `lw £ 3,2. Для балок, рассчитываемых в упругой стадии, допускается превышать указанные выше расстояния между ребрами до значения 3hw при условии передачи нагрузки через сплошной жесткий настил или при значении гибкости сжатого пояса балки λb = lef /bf, не превышающем ее предельного значения λub (в рассматриваемом примере это условие соблюдается: в середине пролета балки λb = 6,67 < λub = 15,64 и в измененном сечении λb = 12,56 < λub = 14,3), и при обязательном обеспечении местной устойчивости элементов балки.

Рис. 3.14. Схема балки, укрепленной поперечными ребрами жесткости
Расстояние между ребрами назначаем  , что увязывается с шагом балок настила
, что увязывается с шагом балок настила  При шаге а = 3 м поперечное ребро жесткости попадает на монтажный стык в середине пролета балки, поэтому первое и последующие за ним ребра смещаем к опоре на расстояние а/2 = 1,5 м.
При шаге а = 3 м поперечное ребро жесткости попадает на монтажный стык в середине пролета балки, поэтому первое и последующие за ним ребра смещаем к опоре на расстояние а/2 = 1,5 м.
Ширина выступающей части парного ребра должна быть не менее
br = hw/30 + 40 = 1500 / 30 + 40 = 90 мм.
для одностороннего – br = hw/24 + 50 = 1500 / 24 + 50 = 112,5 мм.
Толщина ребра

Принимаем ребро жесткости по ГОСТ 103–76* (табл. 3.7) из двух стальных полос 90´7 мм. Ребра жесткости привариваются к стенке непрерывными угловыми швами минимальной толщины. Торцы ребер должны иметь скосы с размерами не менее 40´40 мм для снижения концентрации сварочных напряжений в зоне пересечения сварных швов и пропуска поясных швов балки.
Поперечное ребро жесткости, расположенное в месте приложения сосредоточенной нагрузки Fb = 334,08 кН к верхнему поясу балки проверяют расчетом на устойчивость: двустороннее ребро – как центрально-сжатую стойку, одностороннее – как стойку, сжатую с эксцентриситетом, равным расстоянию от срединной плоскости стенки до центра тяжести расчетного сечения стойки. При этом в расчетное сечение стойки включают сечение ребра жесткости и устойчивые полосы стенки шириной
c = 0,65tw = 0,65 · 1,2
= 0,65 · 1,2  = 22,85 см
= 22,85 см
с каждой стороны ребра, а расчетную длину принимают равной высоте стенки hw = 1500 мм (рис. 3.15).

Рис. 3.15. Расчетное сечение условной стойки
Расчетная площадь стойки при двустороннем ребре
As = (2br+ tw)tr+ 2ctw = (2 · 9 + 1,2) 0,7 + 2 ∙ 22,85 ∙ 1,2) = 68,28 см2.
Момент инерции сечения стойки
Iz = tr3/12 + 2ctw3/12 = 0,7 (2 ∙ 9 +1,2)3 / 12 + 2 ∙ 22,85 ∙ 1,23 / 12 = 412,88 см4.
Радиус инерции
iz =  =
=  = 2,46 см.
= 2,46 см.
Гибкость стойки
λz = lef /iz = 150 / 2,46 = 60,98.
Условная гибкость

Производим проверку устойчивости стойки:

где φ = 0,813 – коэффициент устойчивости при центральном сжатии, принимаемый по табл. 3.11 в зависимости от условной гибкости λz для типа кривой устойчивости ״b״; тип кривой устойчивости зависит от формы сечений и толщины проката (табл. 3.12), при условной гибкости λz ≤ 0,4 коэффициент φ принимается равным единице.
Условие выполняется.
Таблица 3.11
Коэффициенты устойчивости при центральном сжатии
|
Условная гибкость |
Коэффициент j для типов кривых устойчивости |
Условная гибкость |
Коэффициент j для типов кривых устойчивости |
||||
|
a |
b |
c |
a |
b |
c |
||
|
0,4 |
999 |
998 |
992 |
3,2 |
660 |
602 |
526 |
|
0,6 |
994 |
986 |
950 |
3,4 |
615 |
562 |
492 |
|
0,8 |
981 |
967 |
929 |
3,6 |
572 |
524 |
460 |
|
1,0 |
968 |
948 |
901 |
3,8 |
530 |
487 |
430 |
|
1,2 |
954 |
927 |
878 |
4,0 |
475 |
453 |
401 |
|
1,4 |
938 |
905 |
842 |
4,2 |
431 |
421 |
375 |
|
1,6 |
920 |
881 |
811 |
4,4 |
393 |
392 |
351 |
|
1,8 |
900 |
855 |
778 |
4,6 |
359 |
359 |
328 |
|
2,0 |
877 |
826 |
744 |
4,8 |
330 |
330 |
308 |
|
2,2 |
851 |
794 |
709 |
5,0 |
304 |
304 |
289 |
|
2,4 |
820 |
760 |
672 |
5,2 |
281 |
281 |
271 |
|
2,6 |
785 |
722 |
635 |
5,4 |
261 |
261 |
255 |
|
2,8 |
747 |
683 |
598 |
5,6 |
242 |
242 |
240 |
|
3,0 |
704 |
643 |
562 |
5,8 |
226 |
226 |
226 |
П р и м е ч а н и е. Значения коэффициента j в таблице увеличены в 1000 раз.
Устойчивость стенок балок не требуется проверять, если условная гибкость стенки  w не превышает значений:
w не превышает значений:
3,5 – для балок с двухсторонними поясными швами при отсутствии местной нагрузки на пояс балки;
3,2 – для таких же балок с односторонними поясными швами;
2,5 – для балок с двухсторонними поясными швами при наличии местной нагрузки на пояс.
Таблица 3.12
Характеристики кривых устойчивости
|
Тип сечения |
Тип кривой устойчивости |
Значение коэффициентов |
||||
|
α |
β |
λmax |
||||
|
|
a |
0,03 |
0,06 |
3,8 |
||
|
|
b |
0,04 |
0,09 |
4,4 |
||
|
|
c |
0,04 |
0,14 |
5,8 |
||
В нашем примере  следовательно, требуется проверка стенки на местную устойчивость.
следовательно, требуется проверка стенки на местную устойчивость.
Расчет на устойчивость стенки балки симметричного сечения, укрепленной только поперечными основными ребрами жесткости, при отсутствии местных напряжений смятия  и условной гибкости стенки
и условной гибкости стенки  выполняется по формуле
выполняется по формуле

при наличии местного напряжения (см. рис. 3.11) – по формуле

где σ, t и σloc – действующие нормальные, касательные и локальные напряжения в месте соединения стенки с поясом от средних значений M, Q и Fb в пределах отсека; если длина отсека больше его расчетной высоты (a > hw), то M и Q определяются для наиболее напряженного участка отсека с длиной, равной высоте отсека hw; если в пределах отсека M и Q меняют знак, то их средние значения следует вычислять на участке отсека с одним знаком;
σсr , σ loc,сr, τсr – критические напряжения, определяемые по СНиП [6].
Проверку местной устойчивости стенки производят в наиболее нагруженных отсеках: первом от опоры; среднем и, при наличии изменения сечения балки по длине, в отсеке с измененным сечением.
Проверка местной устойчивости стенки в среднем отсеке балки (рис. 3.16).

Рис. 3.16. Распределение изгибающих моментов и поперечных сил
в среднем отсеке
Так как а = 3 м > hw = 1,5 м, определяем Mср и Qср по середине условного отсека шириной, равной половине высоты стенки hw, для чего вычисляем величины моментов и поперечных сил на границах расчетного участка (х1 = 7,5 м; х2 = 9 м):
M1 = qx1(l – x1)/2 = 115,03 · 7,5 (18 – 7,5) / 2 = 4529,31 кН∙м;
M2 = Mmax = 4658,72 кН∙м;
 Q2 = 0;
Q2 = 0;
Mср = (M1 + M2)/2 = (4529,31 + 4658,72) / 2 = 4594,02 кН·м;
Qср = (Q1 + Q2)/2 = 172,55 / 2 = 86,28 кН.
Краевое напряжение сжатия в стенке
σ = Mср(hw/h)/Wx = 4594,02 (150 / 155) /21234 = 20,09 кН/см2.
Среднее касательное напряжение в отсеке
τ = Qср/(hwtw) = 86,28 / (150 ∙ 1,2) = 0,48 кН/см2.
Локальное напряжение σloc = 0.
Критическое нормальное напряжение

где cсr = 33,4 – коэффициент, определяемый по табл. 3.13 в зависимости от значения коэффициента δ, учитывающего степень упругого защемления стенки в поясах,

здесь β = ∞ – при непрерывном опирании плит;
β = 0,8 – в прочих случаях.
Таблица 3.13
Значения коэффициента ссr в зависимости от значения δ
|
d |
£ 0,8 |
1,0 |
2,0 |
4,0 |
6,0 |
10,0 |
³30 |
|
ссr |
30,0 |
31,5 |
33,3 |
34,6 |
34,8 |
35,1 |
35,5 |
Критическое касательное напряжение определяется по формуле

где  – отношение большей стороны отсека a или hw к меньшей d;
– отношение большей стороны отсека a или hw к меньшей d;

здесь d = hw = 1,5 м < a = 3 м.
Проверяем местную устойчивость стенки:

Устойчивость стенки в середине балки обеспечена.
Проверка местной устойчивости стенки в месте изменения сечения балки на расстоянии х = 3 м от опоры.
Расчетные усилия равны:
М1 = 2588,18 кН·м; Q1 = 690,18 кН.
Краевое напряжение сжатия в стенке
σ = M1(hw/h)/W1 = 258818 (150 / 155) /13357 = 18,75 кН/см2.
Среднее касательное напряжение в отсеке
τ = Q1/(hwtw) = 690,18 / (150 ∙ 1,2) = 3,83 кН/см2.
Локальное напряжение σloc = 0.
Критическое нормальное напряжение

где cсr = 31,8 – по табл. 3.13 в зависимости от

Критическое касательное напряжение (см. проверку местной устойчивости стенки в среднем отсеке).
(см. проверку местной устойчивости стенки в среднем отсеке).
Производим проверку:

Стенка в отсеке балки с измененным сечением устойчива.
Проверка местной устойчивости стенки в первом отсеке в сечении на расстоянии от опоры x1 = a1/2 = 1,5 / 2 = 0,75 м (рис. 3.17),
где a1= hw = 1,5 м.

Рис. 3.17. К проверке местной устойчивости стенки балки у опоры
Определяем усилия:
M1 = qx1(l – x1)/2 = 115,03 · 0,75 (18 – 0,75) / 2 = 744,1 кН∙м;

Краевое напряжение сжатия в стенке
σ = M1(hw/h)/W1 = 74410 (150 / 155) /13357 = 5,39 кН/см2.
Среднее касательное напряжение в отсеке
τ = Q1/(hwtw) = 949 / (150 ∙ 1,2) = 5,27 кН/см2.
Локальное напряжение 
Критическое нормальное напряжение
 при d = 1,16.
при d = 1,16.
Критическое касательное напряжение определяется по формуле

где  ;
;

здесь d = hw = a1 = 1,5 м – меньшая из сторон отсека.
Производим проверку:

Стенка в первом от опоры отсеке устойчива.
В случае невыполнения условий устойчивости стенки необходимо увеличить толщину стенки tw или уменьшить расстояние между поперечными ребрами жесткости а, затем повторно произвести проверку ее устойчивости.
Проверка местной устойчивости стенки балки при наличии местных напряжений (σloc ¹ 0). При наличии местных напряжений проверку стенки на местную устойчивость следует выполнять в зависимости от значения a/hw, при этом значения M и Q определяют в одном сечении балки.
Значения критических напряжений определяются в предположении выпучивания стенки между ребрами жесткости при ее потере устойчивости по одной полуволне при частом расположении ребер (a/hw £ 0,8) и при более редкой расстановке ребер жесткости (a/hw > 0,8) – по одной или двум полуволнам.
Значение критического нормального напряжения σcr при a/hw £ 0,8 определяется так же, как и при отсутствии местных напряжений по формуле

где ccr находится по табл. 3.13;
Критическое напряжение потери устойчивости от действия местных напряжений определяется по формуле

где с1 – коэффициент, принимаемый по табл. 3.14 в зависимости от a/hw – соотношения сторон проверяемой пластины и значения, ρ = 1,04lef /hw – относительной длины загружения пластины местной нагрузкой lef к высоте стенки hw (см. рис. 3.11), здесь lef = b + 2tf ;
с2 – коэффициент, принимаемый по табл. 3.15 в зависимости от отношения a/hw и значения δ.
Таблица 3.14
Значения коэффициента c1
|
ρ |
При a/hef или a1/hef, равном |
|||||||||
|
≤0,50 |
0,60 |
0,67 |
0,80 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
≥2,0 |
|
|
0,10 |
56,7 |
46,6 |
41,8 |
34,9 |
28,5 |
24,5 |
21,7 |
19,5 |
17,7 |
16,2 |
|
0,15 |
38,9 |
31,3 |
27,9 |
23,0 |
18,6 |
16,2 |
14,6 |
13,6 |
12,7 |
12,0 |
|
0,20 |
33,9 |
26,7 |
23,5 |
19,2 |
15,4 |
13,3 |
12,1 |
11,3 |
10,7 |
10,2 |
|
0,25 |
30,6 |
24,9 |
20,3 |
16,2 |
12,9 |
11,1 |
10,0 |
9,4 |
9,0 |
8,7 |
|
0,30 |
28,9 |
21,6 |
18,5 |
14,5 |
11,3 |
9,6 |
8,7 |
8,1 |
7,8 |
7,6 |
|
0,35 |
28,0 |
20,6 |
18,1 |
13,4 |
10,2 |
8,6 |
7,7 |
7,2 |
6,9 |
6,7 |
|
0,40 |
27,4 |
20,0 |
16,8 |
12,7 |
9,5 |
7,9 |
7,0 |
6,6 |
6,3 |
6,1 |
Таблица 3.15
Значения коэффициента c2
|
d |
При a/hef или a1/hef, равном |
|||||||
|
0,50 |
0,60 |
0,67 |
0,80 |
1,00 |
1,20 |
1,40 |
≥1,60 |
|
|
≤1 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
|
2 |
1,64 |
1,64 |
1,64 |
1,67 |
1,76 |
1,82 |
1,84 |
1,85 |
|
4 |
1,66 |
1,67 |
1,69 |
1,75 |
1,87 |
2,01 |
2,09 |
2,12 |
|
6 |
1,67 |
1,68 |
1,70 |
1,77 |
1,92 |
2,08 |
2,19 |
2,26 |
|
10 |
1,68 |
1,69 |
1,71 |
1,78 |
1,96 |
2,14 |
2,28 |
2,38 |
|
≥30 |
1,68 |
1,70 |
1,72 |
1,80 |
1,99 |
2,20 |
2,38 |
2,52 |
При отношении a/hw > 0,8 рассматривают два случая проверки устойчивости стенки:
В первом случае вычисляются критическое нормальное σcr и локальное σloc,cr напряжения по следующим формулам:

где ccr определяется по табл. 3.13;

где для его вычисления при определении коэффициентов c1 и c2 по табл. 3.14 и 3.15 вместо a необходимо принять a1 = 0,5a при 0,8 ≤ a/hw ≤ 1,33 и a1 = 0,67 hw при a/hw > 1,33.
Во втором случае их определяют так:
– критическое нормальное напряжение

где ccr определяется по табл. 3.16;
– критическое локальное напряжение потери устойчивости

где коэффициенты c1 и c2 определяют по фактическому отношению сторон a/hw (если a/hw > 2, в расчете принимают a/hw = 2).
Таблица 3.16
Значения коэффициента ccr в зависимости
от отношения a/hw
|
a/hw |
≤ 0,8 |
0,9 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
≥2,0 |
|
cсr |
По табл. 3.13 |
37,0 |
39,2 |
45,2 |
52,8 |
62,0 |
72,6 |
84,7 |
Значение критического касательного напряжения τcr во всех случаях вычисляют по фактическим размерам отсека.
Проверка местной устойчивости стенки при наличии местных напряжений в среднем отсеке (в качестве примера).
При принятом шаге поперечных ребер жесткости а = 3 м отношение 
Первая проверка. Локальное напряжение от сосредоточенной нагрузки sloc = 13,58 кН/см2.
Нормальное напряжение в среднем отсеке s = 20,9 кН/см2.
Среднее касательное напряжение τ = 0,48 кН/см2.
Значение критического нормального напряжения
 44,38 кН/см2,
44,38 кН/см2,
где ccr = 33,4, определенное по табл. 3.13 при δ = 2,16.
Значение критического локального напряжения

где при вычислении коэффициентов с1 и с2 при a/hw = 2 > 1,33 вместо а принимаем а1 = 0,67hw = 0,67 · 150 = 100,5 см, следовательно,
a1/hw = 100,5 / 150 = 0,67;
ρ = 1,04lef /hw = 1,04 ∙ 20,5 / 150 = 0,14 (здесь lef = b + 2tf = 15,5 + 2∙2,5 = = 20,5 см – условная длина распределения сосредоточенной нагрузки);
с1 = 30,68 – коэффициент, определяемый по табл. 3.14 в зависимости от a1/hw = 0,67 и ρ = 0,14;
с2 = 1,64 – коэффициент, определяемый по табл. 3.15 в зависимости от a1/hw = 0,67 и δ = 2,16.
Значение критического касательного напряжения τcr = 9,36 кН/см2.
Проверяем местную устойчивость стенки:
 .
.
Стенка устойчива.
Вторая проверка. Значение критического нормального напряжения

где ccr = 84,7 – коэффициент, определяемый по табл. 3.16 в зависимости от a/hw = 300 / 150 = 2.
Значение критического локального напряжения

где с1 = 12,84 – коэффициент, определяемый по табл. 3.14 в зависимости от a1/hw = 2 и ρ = 0,14;
с2 = 1,87 – коэффициент, определяемый по табл. 3.15 в зависимости от a/hw = 2 и δ = 2,16;
Значение критического касательного напряжения τcr = 9,36 кН/см2.
Проверяем местную устойчивость стенки:
 .
.
Стенка устойчива.
В балках большой высоты (h > 2 м) с тонкой стенкой при условной гибкости  w > 5,5 для обеспечения ее устойчивости рационально, помимо поперечных ребер жесткости, ставить продольные ребра, опирающиеся на поперечные и располагаемые на расстоянии (0,2…0,3)hw от сжатой кромки отсека. Наличие продольного ребра разбивает стенку по высоте на верхнюю и нижнюю пластинки, устойчивость которых проверяется раздельно по СНиП [6].
w > 5,5 для обеспечения ее устойчивости рационально, помимо поперечных ребер жесткости, ставить продольные ребра, опирающиеся на поперечные и располагаемые на расстоянии (0,2…0,3)hw от сжатой кромки отсека. Наличие продольного ребра разбивает стенку по высоте на верхнюю и нижнюю пластинки, устойчивость которых проверяется раздельно по СНиП [6].
3.6.7. Проверка жесткости балки
При равномерно распределенной нагрузке на балку проверка производится по формуле

где α = 1,03 – коэффициент, учитывающий увеличение прогиба балки за счет уменьшения ее жесткости у опор, вызванного изменением сечения балки по длине.
3.6.8. Расчет соединения поясов балки со стенкой
Соединение поясов составной балки со стенкой осуществляется в сварных балках поясными швами, обеспечивающими совместную работу поясов и стенки, тем самым предотвращается при изгибе балки их взаимный сдвиг. Кроме работы на сдвиг при наличии местной нагрузки, действующей на пояс от балок настила в месте, не укрепленном поперечным ребром жесткости, поясные швы испытывают дополнительно срез от местного вертикального давления (рис. 3.18). Соединение выполняется автоматической сваркой угловыми непрерывными швами одинаковой толщины по всей длине балки.

Рис. 3.18. К расчету поясных соединений
Расчет сварного шва производится на усилие, приходящееся на 1 см длины балки, и длина шва соответственно принимается в расчет равной 1 см.
Сравниваем:

где  – при расчете по металлу шва (см. табл. 3.4);
– при расчете по металлу шва (см. табл. 3.4);
βz = 1,15 – при расчете по металлу границы сплавления;
γwf и gwz – коэффициенты условий работы шва, равные 1 во всех случаях, кроме конструкций, возводимых в климатических районах I1, I2, II2 и II3, для которых γwf = 0,85 для металла шва с нормативным сопротивлением  и gwz = 0,85 – для всех сталей;
и gwz = 0,85 – для всех сталей;
Rwf = 180 МПа = 18 кН/см2 – расчетное сопротивление сварного соединения при расчете по металлу шва, принимаемое по табл. 2.7 в зависимости от марки сварочной проволоки, которую выбирают по табл. 2.5 для автоматической сварки стали принятого класса;
 – расчетное сопротивление сварного соединения при расчете по границе сплавления;
– расчетное сопротивление сварного соединения при расчете по границе сплавления;
 – нормативное сопротивление основного металла, принимаемое по табл. 2.3.
– нормативное сопротивление основного металла, принимаемое по табл. 2.3.
Поясные швы при  рассчитываются по металлу границы сплавления по формуле
рассчитываются по металлу границы сплавления по формуле

где  – усилие на единицу длины шва от поперечной силы на опоре Qmax, сдвигающее пояс относительно стенки;
– усилие на единицу длины шва от поперечной силы на опоре Qmax, сдвигающее пояс относительно стенки;
Sf1 = 4575 см3, I1 =1035188 см4 – статический момент пояса и момент инерции относительно нейтральной оси сечения балки на опоре (см стр. 72);
 – давление от сосредоточенной силы Fb на единицу длины шва.
– давление от сосредоточенной силы Fb на единицу длины шва.
Следует иметь в виду, что T и V вычисляются в одном и том же сечении, т.е. там, где σloc ≠ 0. При отсутствии сосредоточенной силы Fb (σloc = 0) второй член под знаком радикала исключается.
Вычисляем усилие:
T = QmaxSf1/I1 = 1033,59 · 4575 / 1035188 = 4,57 кН.
Определяем требуемый катет сварного шва:

где n = 1 при одностороннем шве, n = 2 при двустороннем.
При толщине tf = 25 мм (более толстого из свариваемых элементов) конструктивно принимаем для автоматической сварки минимальный катет шва kf,min = 7 мм (см. табл. 3.5).
3.6.9. Конструирование и расчет опорной части главной балки
Передача нагрузки от главной балки, установленной сверху на колонну, осуществляется через торцевое опорное ребро. Торец ребра рассчитывается на смятие, для чего он строгается. Выступающая часть а не должна быть больше 1,5tr (рис. 3.19) и обычно принимается 15 – 20 мм.

Рис. 3.19. К расчету опорной части балки
Расчет ребра производится на усилие Fb, равное опорной реакции балки:

Определяем площадь смятия торца ребра:
Ar = brtr = Fb/(Rpγc) = 1033,59 / (33,6 · 1) = 30,76 см2,
где  – расчетное сопротивление стали смятию торцевой поверхности (при наличии пригонки), принимаемое по табл. 2.4 для класса стали С255 с Run = 370 МПа.
– расчетное сопротивление стали смятию торцевой поверхности (при наличии пригонки), принимаемое по табл. 2.4 для класса стали С255 с Run = 370 МПа.
Принимая ширину ребра равной ширине пояса балки у опоры bh = bf1 = 240 мм, определяем толщину ребра:

По конструктивным соображениям рекомендуется размеры опорного ребра принимать:  ;
; 
Принимаем ребро из листа 240´16 мм с площадью Ar = 38,4 см2.
Толщина опорного ребра должна быть не менее 
где br,ef = br/2 = 240 / 2 = 120 мм – ширина выступающей части:
tr = 1,6 см > 3 · 12
Опорная часть главной балки из своей плоскости (относительно оси z–z) проверяется на устойчивость как условная центрально-сжатая стойка с расчетной длиной, равной высоте стенки  . Расчет на устойчивость стойки сплошного сечения при центральном сжатии выполняют по формуле
. Расчет на устойчивость стойки сплошного сечения при центральном сжатии выполняют по формуле

где φ – коэффициент устойчивости при центральном сжатии, принимаемый в зависимости от условной гибкости  по табл. 3.11 для типа кривой устойчивости “с” (см. табл. 3.12).
по табл. 3.11 для типа кривой устойчивости “с” (см. табл. 3.12).
Расчетное сечение условной стойки включает в себя площадь опорного ребра Ar и площадь устойчивого участка стенки, примыкающего к ребру, шириной

Определяем геометрические характеристики стойки:
– площадь
As = Ar + ctw = 38,4 + 22,85 ∙ 1,2 = 65,82 см2;
– момент инерции

– радиус инерции

– гибкость
λz = hw/iz = 150 / 5,3 = 28,3;
– условная гибкость

Коэффициент устойчивости φ = 0,907.
Производим проверку:


Опорная часть балки устойчива.
Прикрепление опорного ребра к стенке балки осуществляем механизированной сваркой в среде углекислого газа проволокой Св-08Г2С по ГОСТ 2246-70* для сварки стали класса С255 (см. табл. 2.5; 2.7 и 3.4):
Rwf = 21,5 кН/см2 ; Rwz = 16,65 кН/см2 ; βz = 1,05
βz = 1,05
Сравниваем:

следовательно, расчетным является сечение по металлу границы сплавления.
Условие прочности сварных угловых швов, работающих на срез:

откуда катет шва

Принимаем шов с kf = 7 мм, что больше kf,min = 5 мм по табл. 3.5.
Проверяем максимальную длину расчетной части шва:

укладывается в конструктивную длину шва, равную высоте стенки.
Ребро привариваем к стенке по всей высоте непрерывными швами.
Главные балки скрепляют на опоре между собой через прокладку толщиной, равной конструктивному зазору, и с колонной монтажными болтами диаметром 16 – 20 мм, фиксирующими проектное положение балок. Болты взаимного сопряжения балок размещают в нижней зоне балки, что позволяет считать его шарнирным, так как допускается некоторый поворот опорного сечения балок за счет податливости болтового соединения.
3.6.10. Проектирование монтажного стыка главной балки
По условиям перевозки (ограничение массы и габаритов) балка расчленяется по возможности на одинаковые отправочные элементы (марки). В разрезной балке монтажный стык выполняется в одном сечении (универсальный стык) и чаще располагается в середине пролета, где Mmax и соответственно максимальные нормальные напряжения σ близки к расчетному сопротивлению основного металла Ry.
Монтажный стык на сварке. Стык элементов балки осуществляется стыковыми швами (рис. 3.20). Расчетные сопротивления сварных соединений для любого вида сварки принимаются (см. табл. 2.6): при сжатии соединения независимо от методов контроля качества швов Rwy = Ry; при растяжении и изгибе с физическим контролем качества швов Rwy = Ry и Rwy = 0,85Ry, если физические методы контроля не используются.

Рис. 3.20. Монтажный стык главной балки на сварке
На монтаже применение физических способов контроля затруднено, поэтому расчет растянутого стыкового соединения производится по его пониженному расчетному сопротивлению. Сжатый верхний пояс и стенка соединяются прямым швом, растянутый пояс – косым швом для увеличения длины шва, так как действительное напряжение в поясе σ превышает Rwy. Для обеспечения равнопрочности сварного стыка и основного сечения нижнего пояса достаточен скос с наклоном реза 2:1.
Монтажный стык выполняется ручной сваркой, материалы для сварки выбираются по табл. 2.5. Для сварки монтажного стыка применяют электроды с индексом А (Э42А), обеспечивающие повышенную пластичность наплавленного металла.
Для обеспечения качественного соединения при ручной сварке элементов толщиной более 8 – 10 мм производится V-образная разделка кромок, начало и конец шва выводятся на специальные технологические планки.
Для уменьшения сварочных напряжений соблюдается определенный порядок сварки (см. рис. 3.20): сначала сваривают поперечные стыковые швы стенки 1, поясов 2 и 3, имеющие наибольшую поперечную усадку, последними заваривают угловые швы 4 и 5, имеющие небольшую продольную усадку. Оставленные незаверенными на заводе участки поясных швов длиной около 500 мм дают возможность поясным листам несколько вытянуться при усадке швов 2. Это также позволяет при монтаже совместить торцы свариваемых элементов отправочных марок, имеющих отклонение в размерах в пределах технологических допусков.
Монтажный стык на высокопрочных болтах. Монтажные стыки на высокопрочных болтах выполняются с накладками (по три на каждом поясе и по две на стенке, рис. 3.21).

Рис. 3.21. Монтажный стык главной балки на высокопрочных болтах
Усилие с одного элемента на другой передается за счет сил трения, возникающих между соприкасающимися плоскостями, стянутыми высокопрочными болтами. Площади сечения накладок должны быть не меньше площади сечения перекрываемого ими элемента. Рекомендуемые к применению в конструкциях средней мощности высокопрочные болты и их площади сечения приведены в табл. 3.17.
Таблица 3.17
Площади сечения болтов
|
Площадь, см2 |
Диаметр db, мм |
|||
|
16 |
20 |
24 |
30 |
|
|
Ab |
2,01 |
3,14 |
4,52 |
7,06 |
|
Abn |
1,57 |
2,45 |
3,52 |
5,60 |
Принимаем болты db = 24 мм. Диаметр отверстия d под болт делается на 2 – 3 мм больше db. Назначаем отверстие d = 26 мм.
Размещение болтов производится согласно требованиям, приведенным в табл. 3.18.
Минимальное расстояние между центрами болтов (шаг болтов) в расчетных соединениях определяется условиями прочности основного металла и принимается в любом направлении равным amin = 2,5d = 2,5 · 26 = 65 мм. Принимаем а = 70 мм.
Максимальное расстояние между болтами определяется устойчивостью сжатых частей элементов в промежутках между болтами (в крайних рядах при отсутствии окаймляющих уголков amax ≤ 12tmin = 12 · 10 = 120 мм, где tmin – толщина наиболее тонкого наружного элемента) и обеспечением плотности соединения:  Минимальное расстояние от центра болта до края элемента для высокопрочных болтов в любом направлении усилия сmin ≥ 1,3d = 1,3 · 26 = 33,8 мм.
Минимальное расстояние от центра болта до края элемента для высокопрочных болтов в любом направлении усилия сmin ≥ 1,3d = 1,3 · 26 = 33,8 мм.
Принимаем с = 50 мм. Ширина верхней накладки пояса назначается равной ширине пояса балки bnf = bf = 450 мм.
Ширина каждой нижней накладки пояса определяется:
b′nf = [bf – (tw + 2kf + 2Δ)] / 2 = [450 – (12 + 2 ∙ 7 + 2 ∙ 10)] / 2 = 202 мм,
где Δ = 10…15 мм – конструктивный зазор.
Толщина каждой накладки пояса
tnf = tf/2 + 2 = 25 / 2 + 2 = 14,5 мм.
Принимаем верхнюю накладку из листа 450´14 мм с площадью сечения Аnf = 63 см2 и две нижних накладки из листа 200´14 мм с площадью сечения А′ nf = 28 см2.
Таблица 3.18
Нормы расстановки болтов в болтовых соединениях
|
Характеристика расстояния |
Расстояние при размещении болтов |
|
1. Расстояния между центрами болтов в любом направлении: а) минимальное б) максимальное в крайних рядах при отсутствии окаймляющих уголков при растяжении и сжатии в) максимальное в средних рядах, а также в крайних рядах при наличии окаймляющих уголков: при растяжении при сжатии |
2,5d* 8d или 12t 16d или 24t 12d или 18t |
|
2. Расстояния от центра болта до края элемента: а) минимальное вдоль усилия б) то же, поперек усилия: при обрезных кромках при прокатных кромках в) максимальное г) минимальное для высокопрочных болтов при любой кромке и любом направлении усилия |
2d 1,5d 1,2d 4d или 8t 1,3d |
* В соединяемых элементах из стали с пределом текучести свыше 380 МПа минимальное расстояние между болтами следует принимать равным 3d.
Обозначения, принятые в таблице:
d – диаметр отверстия для болта;
t – толщина наиболее тонкого наружного элемента.
Суммарная площадь накладок
Аn = Аnf + 2А′nf = 63 + 2 ∙ 28 = 119 см2 > Аf = 112,5 см2.
Горизонтальные болты располагаем в 4 ряда на одной полунакладке.
Определяем длину двух вертикальных накладок:
lnw = hw – 2(tnf + Δ) = 1500 – 2 (14 + 10) = 1450 мм.
Ширина вертикальных накладок
bnw = 2а + δ + 4c = 2 · 70 + 10 + 4 · 50 = 350 мм,
где δ = 10 мм – зазор между элементами.
Толщину одной вертикальной накладки tnw принимаем равной толщине стенки tw за вычетом 2 мм (tnw = 10 мм).
Максимальное расстояние между крайними горизонтальными рядами болтов (с учетом расстояния до края элемента с = 50 мм)
а1= 1450 – 2 ∙ 50 = 1350 мм.
Стык осуществляем высокопрочными болтами db = 24 мм из стали 40Х «селект», имеющей наименьшее временное сопротивление
Rbun = 1100 МПа = 110 кН/см2 (табл. 3.19).
Таблица 3.19
Механические свойства высокопрочных болтов по ГОСТ 22356–77*
|
Номинальный диаметр резьбы d, мм |
Сталь по ГОСТ 4543-71* |
Наименьшее временное сопротивление Rbun, МПа |
|
От 16 до 27 |
40Х “селект” |
1100 |
|
З0Х3МФ 30Х2НМФА |
1350 |
|
|
30 |
40Х “селект” |
950 |
|
30Х3МФ, 35Х2АФ |
1200 |
|
|
36 |
40Х “селект” |
750 |
|
30Х3МФ |
1100 |
Способ регулирования натяжения высокопрочных болтов принимаем по M (моменту закручивания). Расчетное усилие Qbh, которое может быть воспринято каждой поверхностью трения соединяемых элементов, стянутых одним высокопрочным болтом, определяется по формуле

где  – расчетное сопротивление растяжению высокопрочного болта;
– расчетное сопротивление растяжению высокопрочного болта;
Abn = 3,52 см2 – площадь сечения нетто болта db = 24 мм, принимаемая по табл. 3.17;
 – коэффициент трения, принимаемый в зависимости от обработки поверхностей по табл. 3.20 (принят газопламенный способ обработки поверхностей);
– коэффициент трения, принимаемый в зависимости от обработки поверхностей по табл. 3.20 (принят газопламенный способ обработки поверхностей);
 – коэффициент надежности, принимаемый при статической нагрузке и разности номинальных диаметров отверстий и болтов δ = (d – db) = 1 – 4 мм с использованием регулирования натяжения болтов по М при газопламенном способе обработки поверхностей;
– коэффициент надежности, принимаемый при статической нагрузке и разности номинальных диаметров отверстий и болтов δ = (d – db) = 1 – 4 мм с использованием регулирования натяжения болтов по М при газопламенном способе обработки поверхностей;
gb – коэффициент условий работы соединения, зависящий от количества болтов n, необходимых для восприятия расчетного усилия, и принимаемый равным:
0,8 при n < 5; 0,9 при 5 £ n < 10; 1,0 при n ³ 10.
Таблица 3.20
Коэффициенты трения m и надежности gh
|
Способ обработки (очистки) соединяемых поверхностей |
Способ регулирования натяжения болтов по: |
Коэффициент трения m |
Коэффициенты gh при нагрузке и при разности номинальных диаметров отверстий и болтов d, мм |
|
|
динамической и при d = 3 – 6; статической и при d = 5 – 6 |
динамической и при d = 1; статической и при d = 1 – 4 |
|||
|
Дробеметный или дробеструйный двух поверхностей без консервации |
М a |
0,58 0,58 |
1,35 1,20 |
1,12 1,02 |
|
То же, с консервацией (металлизацией распылением цинка или алюминия) |
М a |
0,50 0,50 |
1,35 1,20 |
1,12 1,02 |
|
Дробью одной поверхности с консервацией полимерным клеем и посыпкой карборундовым порошком, стальными щетками другой поверхности без консервации |
М a |
0,50 0,50 |
1,35 1,20 |
1,12 1,02 |
|
Газопламенный двух поверхностей без консервации |
М a |
0,42 0,42 |
1,35 1,20 |
1,12 1,02 |
|
Стальными щетками двух поверхностей без консервации |
М a |
0,35 0,35 |
1,35 1,25 |
1,17 1,06 |
|
Без обработки |
М a |
0,25 0,25 |
1,70 1,50 |
1,30 1,20 |
П р и м е ч а н и я: 1. Способ регулирования натяжения болтов по М означает регулирование по моменту закручивания, а по a – по углу поворота гайки.
2. Допускаются другие способы обработки соединяемых поверхностей, обеспечивающие значения коэффициентов трения m не ниже указанных в таблице.
Определяем:

Расчет стыков поясов и стенки производим раздельно. Приравнивая кривизну балки в целом  (здесь r – радиус кривизны) кривизне ее составляющих – стенки Mw /(EIw) и поясов Mf /(EIf), находим изгибающие моменты, приходящиеся на стенку Mw и пояса Mf, которые распределяются пропорционально их жесткостям, соответственно EIw и ЕIf.
(здесь r – радиус кривизны) кривизне ее составляющих – стенки Mw /(EIw) и поясов Mf /(EIf), находим изгибающие моменты, приходящиеся на стенку Mw и пояса Mf, которые распределяются пропорционально их жесткостям, соответственно EIw и ЕIf.
Момент инерции стенки Iw = 337500 см4.
Момент инерции поясов

Изгибающий момент, приходящийся на стенку:
Mw = Mmax(Iw/Ix) = 4658,72 (337500 / 1645664) = 955,43 кН/м.
Изгибающий момент, приходящийся на пояса:
Mf = Mmax(If /Ix) = 4658,72 (1308164 / 1645664) = 3703,29 кН/м.
Расчет стыка пояса. Раскладывая изгибающий момент Mf на пару сил, определяем расчетное усилие в поясе:
Nf = Mf //hf = 3703,29 / 152,5 = 2428,39 кН.
Количество болтов n на каждую сторону от центра стыка балки для прикрепления накладок пояса определяем по формуле

где ks = 2 – количество поверхностей трения соединяемых элементов.
Принимаем 12 болтов и размещаем их согласно рис. 3.21.
Длину горизонтальных накладок назначаем конструктивно из условия размещения болтов:
lnf = 2(n1a + 2c) + δ = 2 (2 ∙ 70 +2 ∙ 50) + 10 = 490 мм,
где n1 = (3 – 1) – количество рядов болтов на полунакладке за минусом 1.
Расчет стыка стенки. Расчетный момент, приходящийся на стенку, уравновешивается суммой внутренних пар усилий, действующих на болты. Максимальное горизонтальное усилие Nmax от изгибающего момента, действующее на каждый крайний наиболее напряженный болт, не должно быть больше несущей способности Qbhks.
Условие прочности соединения:
Nmax = Mw amax/(mΣai2) ≤ Qbhks,
где аi – соответствующее расстояние между парами сил в болтах;
m – число вертикальных рядов болтов на полунакладке.
Для определения числа рядов болтов по вертикали k и назначения их шага а вычисляем коэффициент стыка:
a = Mw/(mamaxQbhks) = 95543 / (2 × 135 × 101,64 × 2) = 1,74.
Принимаем по табл. 3.21 число горизонтальных рядов болтов k = 8.
Таблица 3.21
Коэффициенты стыка стенки балок a
|
Число рядов по вертикали k |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
a |
1,4 |
1,55 |
1,71 |
1,87 |
2,04 |
2,20 |
2,36 |
2,52 |
2,69 |
2,86 |
Определяем шаг болтов по вертикали:
a = amax/(k – 1) = 135 / (8 – 1) = 19,29 см.
Шаг a округляется до 5 мм и должен укладываться целое число раз в расстояние между крайними рядами болтов a1. Окончательно принимаем по высоте накладки 8 рядов болтов с шагом а = 200 мм, что меньше amax = 208 мм. Максимальное расстояние между крайними горизонталь- ными рядами болтов а1 = (8 – 1) 200 = 1400 мм и а2 = 1000 мм, а3 = 600 мм, а4 = 200 мм (см. рис. 3.21).
Длина вертикальных накладок (при с = 35мм > сmin = 33,8 мм)
lnw = (k – 1)a + 2c = (8 – 1) 200 + 2 ∙ 35= 1470 мм.
Проверяем стык стенки по прочности наиболее нагруженного болта:
Nmax = 955,43 · 1,4 / [2 (1,42 + 12 + 0,62 + 0,22)] =
= 199,05 кН < Qbhksγс = 101,64 · 2 · 1 = 203,28 кН.
Условие выполняется.
При наличии в месте стыка поперечной силы Q стык стенки рассчитывается на совместное действие поперечной силы Q и части изгибающего момента, воспринимаемого стенкой Mw. Наиболее напряженный крайний болт рассчитывается на равнодействующую усилий по формуле

где V = Q/n – вертикальная составляющая усилия, действующая на один
болт в предположении, что поперечная сила Q полностью передается на стенку и принимается распределенной равномерно на все болты n, расположенные на полунакладке с одной стороны стыка.
Проверяем элементы, ослабленные отверстиями под болты d = 26 мм.
Расчет на прочность соединяемых элементов, ослабленных отверстиями под высокопрочные болты, следует выполнять с учетом того, что половина усилия, приходящаяся на каждый болт, в рассматриваемом сечении уже передана силами трения. При этом проверку ослабленных сечений следует производить: при динамических нагрузках – по площади сечения нетто An, при статических нагрузках – по площади сечения брутто A при An ≥ 0,85A либо по условной площади Ac = 1,18An при An < 0,85A.
Пояс ослаблен по краю стыка четырьмя отверстиями (nas = 4) сечением
Adf = nasdtf = 4 · 2,6 · 2,5 = 26 см2.
Площадь сечения нетто пояса определится:
An,f = Af – Adf = 45 · 2,5 – 26 = 86,5 см2 < 0,85Af = 0,85 ∙ 112,5 = 95,63 см2.
Проверку ослабленного сечения пояса производим по условной площади Ac,f = 1,18An,f = 1,18 ∙ 86,5 = 102,07 см2.
Полагая, что половина усилия, приходящаяся на каждый болт, воспринимается силами трения, расчетное усилие в поясе и накладках, ослабленных четырьмя болтами в крайнем ряду, определяется по формуле

Производим проверку прочности ослабленного пояса:

Прочность пояса в месте монтажного стыка обеспечена.
Ослабление накладок четырьмя отверстиями (nas = 4) по крайнему ряду
Adn = nasnndtnf = 4 · 2 · 2,6 · 1,4 = 29,12 см2.
Площадь сечения нетто накладок

“Патофизиология обмена витаминов и микроэлементов” – тут тоже много полезного для Вас.
Условная площадь
Ac,n = 1,18An,nf = 1,18 ∙ 89,88 = 106,06см2.
Производим проверку прочности накладок:

Прочность накладок обеспечена.
При необходимости увеличивается толщина накладок tnf.

Пример решения задачи по подбору минимальных размеров балки прямоугольного поперечного сечения, обеспечивающих её необходимую прочность.
Задача
Для заданной стальной балки подобрать размеры прямоугольного поперечного сечения по условию прочности.
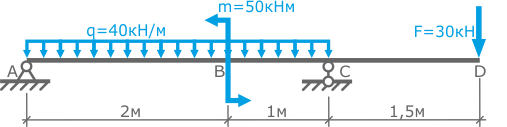
Соотношение сторон сечения h=2b (h – высота, b – ширина).
Полученные размеры принять согласно ГОСТ 6636.
Допустимые напряжения для материала балки [σ]=160МПа.
Другие примеры решений >
Помощь с решением задач >
Решение
Предыдущие пункты решения задачи:
- Определение опорных реакций
- Построение эпюр внутренних поперечных сил и изгибающих моментов
- Расчет момента сопротивления сечения балки по условию прочности
Минимально необходимый расчетный момент сопротивления сечения балки составил
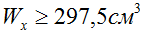
В случаях, когда система изгибающих нагрузок действующих на балку расположена в вертикальной плоскости сечение тоже следует располагать вертикально.
По справочнику находим формулу осевого момента сопротивления прямоугольного сечения
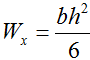
Используя заданное соотношение сторон (h=2b), уменьшим количество переменных в выражении
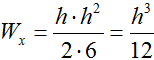
и запишем необходимое неравенство
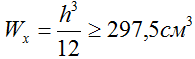
откуда находим расчетную высоту прямоугольного сечения
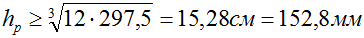
Из заданного соотношения сторон определяем расчетную ширину сечения
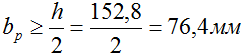
Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки.
При отсутствии дополнительных условий расчетные размеры можно округлить до целого значения в миллиметрах исключительно в большую сторону (h=153мм, b=77мм).
По ГОСТ 6636 нормальных линейных размеров выбираются ближайшие значения в сторону увеличения.
Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=155мм, b=80мм.
После принятия размеров согласно ГОСТ заданное соотношение сторон может несколько измениться. Это нормально.
Оценка экономичности сечений >
Построение эпюры нормальных напряжений >
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Для того, чтобы соорудить надежное деревянное перекрытие, необходимо правильно подобрать размеры балок, а для этого необходимо сделать их расчет. Деревянные балки перекрытия имеют следующие основные размеры: длину и сечение. Их длина определяется шириной пролета, который требуется перекрыть, а сечение зависит как от нагрузки, которая будет на них действовать, от длины пролета и шага установки, то есть расстояния между ними. В данной статье мы рассмотрим, как самостоятельно сделать такой расчет и правильно подобрать размеры балок.
Содержание статьи:
Расчет балок деревянного перекрытия
Для того, чтобы определить какое количество деревянных балок и каких размеров потребуется для устройства перекрытия необходимо:
- замерить пролет, который они будут перекрывать;
- определиться со способами их закрепления на стенах (на какую глубину они будут заходить в стены);
- сделать расчет нагрузки, которая будет на них действовать при эксплуатации;
- с помощью таблиц или программы-калькулятора подобрать подходящие шаг и сечение.
Теперь рассмотрим, как это можно сделать.
Длина деревянных балок перекрытия
Необходимая длина балок перекрытия определяется размерами того пролета, который они будут перекрывать и запасом необходимым для заделывания их в стены. Длину пролета несложно замерить с помощью рулетки, а глубина заделывания в стены, во многом, зависит от их материала.
В домах со стенами из кирпича или блоков балки обычно заделываются в «гнезда» на глубину не менее 100 мм (доска) или 150 мм (брус). В деревянных домах их, как правило, укладываютс в специальные зарубки на глубину не меньше чем 70 мм. При использовании специального металлического крепления (хомутов, уголков, кронштейнов) длина балок будет равна пролету — расстоянию между противоположными стенами, на которых они крепятся. Иногда, при монтаже стропильных ног крыши непосредственно на деревянные балки, их выпускают наружу, за пределы стен на 30-50 см, формируя, таким образом, свес крыши.
Оптимальный пролет, которые могут перекрывать деревянные балки 2,5-4 м. Максимальная длина балки из обрезной доски или бруса, то есть пролет, который она может перекрывать — 6 м. При большей длине пролета (6-12 м) необходимо использовать современные деревянные балки из клееного бруса или двутавровые, а также можно опирать их на промежуточные опоры (стены, колонны). Кроме этого для перекрытия пролетов, длиной более 6 м, вместо балок можно использовать деревянные фермы.
Определение нагрузки, действующей на перекрытие
Нагрузка, действующая на перекрытие по деревянным балкам состоит из нагрузки от собственного веса элементов перекрытия (балок, межбалочного заполнения, зашивки) и постоянной или временной эксплуатационной нагрузки (мебели, различных бытовых устройств, материалов, вес людей). Она, как правило, зависит от вида перекрытия и условий его эксплуатации. Точный расчет таких нагрузок довольно громоздкий и выполняется специалистами при проектировании перекрытия, но при желании выполнить его самостоятельно, можно использовать упрощенный его вариант, приведенный ниже.
Для чердачного деревянного перекрытия, которое не используется для складирования вещей или материалов, с легкими утеплителем (минеральная вата или др.) и подшивкой постоянная нагрузка (от собственного веса — Рсобств.) обычно принимается в пределах 50 кг/м2.
Эксплуатационная нагрузка (Рэкспл.)для такого перекрытия (согласно СНиП 2.01.07-85) составит:
70х1,3 = 90 кг/м 2 , где 70 – нормативное значение нагрузки для такого вида чердака, кг/м2, 1,3 – коэффициент запаса.
Общая расчетная нагрузка, которая будет действовать на данное чердачное перекрытие составит:
Робщ.=Рсобств.+Рэкспл. = 50+90=130 кгм 2 . Округляя в большую сторону принимаем 150 кг/м 2 .
В случае, если в конструкции чердачного помещения будет использоваться более тяжелый утеплитель, материал для межбалочного заполнения или подшивка, а также если предполагается его использовать для хранения вещей или материалов, то есть оно будет интенсивно эксплуатироваться, то нормативное значение нагрузки следует увеличить до 150 кг/м2. В этом случае, общая нагрузка на перекрытие составит:
50+150х1,3 = 245 кг/м 2 , округляем до 250 кг/м 2 .
При использовании чердачного пространства для устройства мансарды, необходимо учесть вес полов, перегородок, мебели. В этом случае общую расчетную нагрузку необходимо увеличить до 300-350 кг/м 2 .
В связи с тем, что междуэтажное деревянное перекрытие, как правило, включает в свою конструкцию полы, а временная эксплуатационная нагрузка включает в себя вес большого количества предметов быта и максимальное присутствие людей, то оно должно быть рассчитано на общую нагрузку 350 — 400 кг/м 2 .
Сечение и шаг балок деревянного перекрытия
Зная необходимую длину балок деревянного перекрытия (L) и определив общую расчетную нагрузку можно определить необходимое их сечение (или диаметр) и шаг укладки, которые связаны между собой. Считается, что лучшим является прямоугольное сечение балки деревянного перекрытия, с соотношением высоты (h) и ширины (s) как 1,4:1. Ширина балок, при этом, может быть в пределах 40-200 мм, а высота 100-300 мм. Высоту балок часто выбирают такой, чтобы она соответствовала необходимой толщине утеплителя. При использовании в качестве балок бревен их диаметр может быть в пределах 11-30 см.
В зависимости от вида и сечения используемого материала, шаг балок деревянного перекрытия может быть от 30 см до 1,2 м, но чаще всего он выбирается в пределах 0,6-1,0 м. Иногда его выбирают таким, чтобы он соответствовал размеру плит утеплителя, укладываемых в межбалочное пространство, или листов подшивки потолка . Кроме этого, в каркасных зданиях, желательно, чтобы шаг укладки балок соответствовал шагу стоек каркаса — в этом случае будет обеспечена наибольшая жесткость и надежность конструкции.
Сделать расчет или проверку уже выбранных размеров деревянных балок перекрытия можно по справочным таблицам (некоторые приведены ниже) или используя онлайн калькулятор “расчет деревянных балок перекрытия”, который легко найти в интернете, «забив» соответствующий запрос в поисковике. При этом необходимо учесть, что относительный их прогиб для чердачных перекрытий не должен быть более 1/250, а для междуэтажных – 1/350.
Таблица 1
Рекомендуемое сечение балок из бруса (s x h), в зависимости от шага их укладки и перекрываемого пролета, при общей расчетной нагрузке 350-400 кг/м 2 (междуэтажные перекрытия), мм:
Шаг,м Пролет,м












