Вы уже знакомы с пирамидой, т. е. многогранником, одна грань которого является многоугольником, а остальные грани-треугольники имеют общую вершину.
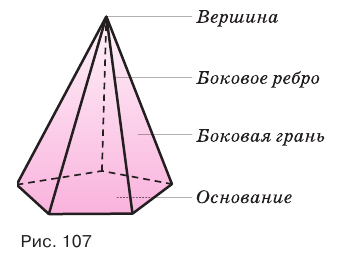
Треугольные грани пирамиды, имеющие общую вершину, называют боковыми гранями, а эту общую вершину — вершиной пирамиды. Ребра боковых граней, сходящиеся в вершине пирамиды, называют боковыми ребрами пирамиды. Многоугольник, которому не принадлежит вершина пирамиды, называют основанием пирамиды (рис. 107).
Пирамиды разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Пирамида, изображенная на рисунке 107, — пятиугольная, а на рисунке 108, — восьмиугольная. Треугольную пирамиду называют еще тетраэдром. У тетраэдра все грани являются треугольниками (рис. 109).
Перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания, называется высотой пирамиды. На рисунке 108 показана высота 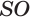
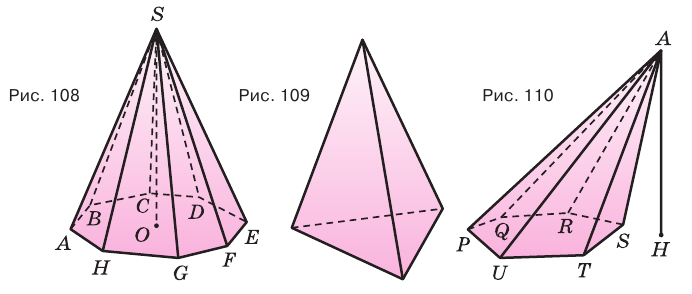
Плоскость, проходящая через два боковых ребра пирамиды, не принадлежащие одной грани, называется диагональной плоскостью, а сечение пирамиды диагональной плоскостью — диагональным сечением. На рисунке 111 показано диагональное сечение шестиугольной пирамиды.
Пирамида, основанием которой является правильный многоугольник, а основание ее высоты совпадает с центром этого многоугольника, называется правильной пирамидой (рис. 112).
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды.
Отметим, что в правильной пирамиде:
- боковые ребра равны;
- боковые грани равны;
- апофемы, равны;
- двугранные углы при основании равны;
- двугранные углы при боковых ребрах равны;
- каждая точка высоты равноудалена от вершин основания;
- каждая точка высоты равноудалена от ребер основания;
- каждая точка высоты равноудалена от боковых граней.
Отметим, что если в пирамиде равны все:
- боковые ребра, то около ее основания можно описать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 113);
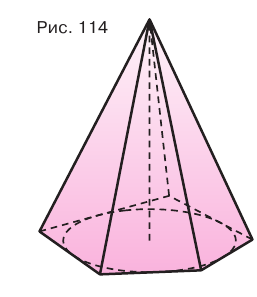
- двугранные углы при основании, то в это основание можно вписать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 114).
Боковые грани составляют боковую поверхность пирамиды, а боковые грани вместе с основанием — полную поверхность пирамиды.
Вы знаете, что боковая поверхность правильной пирамиды равна произведению полупериметра ее основания и апофемы.
Теорема 1.
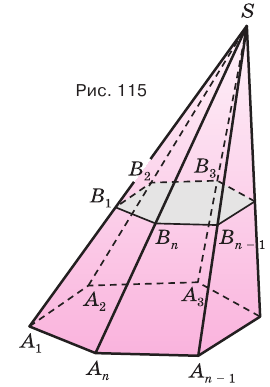
Если пирамиду пересечь плоскостью, параллельной основанию, то:
- а) боковые ребра и высота разделяются на пропорциональные части;
- б) в сечении получается многоугольник, подобный основанию;
- в) площади сечения и основания относятся как квадраты их расстояний от вершины пирамиды.
Используя рисунок 115, докажите эту теорему самостоятельно.
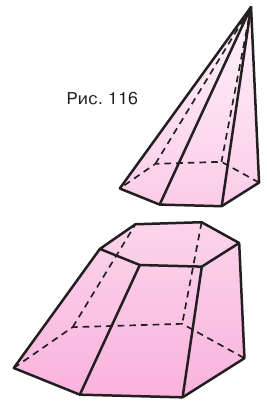
Секущая плоскость, параллельная основанию пирамиды, разделяет ее на две части (рис. 116). Одна из этих частей также является пирамидой, а другая — многогранником, который называется усеченной пирамидой.
Параллельные грани усеченной пирамиды называются ее основаниями (рис. 117). Основания усеченной пирамиды — подобные многоугольники, стороны которых попарно параллельны, поэтому ее боковые грани являются трапециями.
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-либо точки одного основания пирамиды к плоскости другого основания.
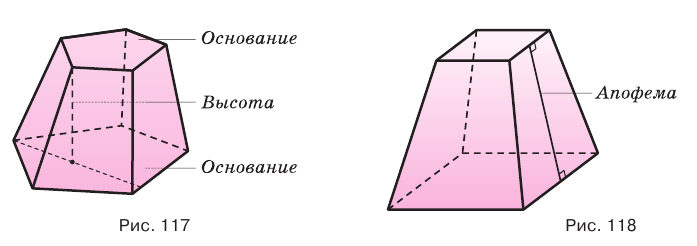
Усеченная пирамида называется правильной, если она является частью правильной пирамиды. Высота боковой грани правильной усеченной пирамиды называется апофемой усеченной пирамиды. На рисунке 118 показана четырехугольная правильная усеченная пирамида и одна из ее апофем.
Теорема 2.
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований и апофемы:
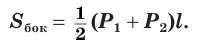
Доказательство:
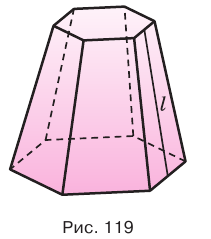
Пусть есть правильная 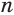 -угольная усеченная пирамида (рис. 119). Пусть
-угольная усеченная пирамида (рис. 119). Пусть 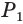 и
и 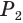 — соответственно периметры нижнего и верхнего оснований и
— соответственно периметры нижнего и верхнего оснований и 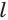 — апофема пирамиды.
— апофема пирамиды.
Боковая поверхность данной пирамиды состоит из 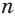 равных трапеций. Пусть
равных трапеций. Пусть 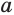 и
и 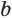 — основания одной из этих трапеций, тогда ее площадь равна
— основания одной из этих трапеций, тогда ее площадь равна 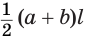 . Учитывая, что боковая поверхность пирамиды состоит из
. Учитывая, что боковая поверхность пирамиды состоит из 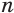 таких трапеций, получим, что
таких трапеций, получим, что
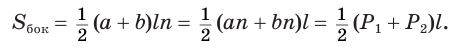
Теперь установим формулу для вычисления объема пирамиды.
Тела, имеющие равные объемы, называются равновеликими.
Теорема 3.
Треугольные пирамиды с равновеликими основаниями и равными высотами равновелики.
Доказательство:
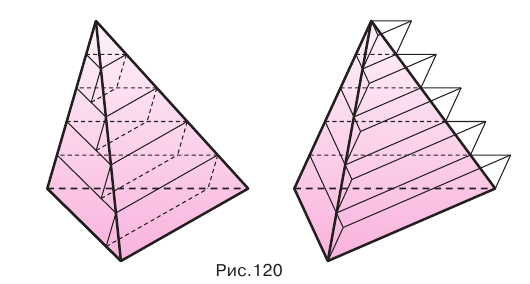
Пусть есть две треугольные пирамиды с равновеликими основаниями и равными высотами (рис. 120). Разделим высоты одной и другой пирамид на 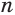 долей и через точки деления проведем плоскости, параллельные основаниям. Этим самым пирамиды разделяются на
долей и через точки деления проведем плоскости, параллельные основаниям. Этим самым пирамиды разделяются на 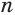 частей. Для каждой части первой пирамиды построим наибольшие по объему призмы, целиком содержащиеся в пирамиде, а для каждой части другой пирамиды — наименьшие по объему призмы, целиком содержащие эту часть.
частей. Для каждой части первой пирамиды построим наибольшие по объему призмы, целиком содержащиеся в пирамиде, а для каждой части другой пирамиды — наименьшие по объему призмы, целиком содержащие эту часть.
Пусть 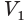 и
и 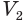 — объемы первой и второй пирамид, a
— объемы первой и второй пирамид, a  и
и  — суммарные объемы призм, построенных для этих пирамид. При счете от оснований пирамид призма в
— суммарные объемы призм, построенных для этих пирамид. При счете от оснований пирамид призма в 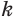 -й части первой пирамиды равновелика призме для
-й части первой пирамиды равновелика призме для 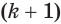 -й части второй пирамиды, так как у этих призм равновелики основания и равные высоты. Поэтому объем
-й части второй пирамиды, так как у этих призм равновелики основания и равные высоты. Поэтому объем  больше объема
больше объема  на объем первой призмы, у которой основанием является основание второй пирамиды, а высота равна
на объем первой призмы, у которой основанием является основание второй пирамиды, а высота равна 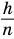 , где
, где 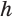 — высота пирамиды (см. рис. 120), т.е.
— высота пирамиды (см. рис. 120), т.е. 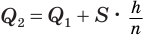 , или
, или 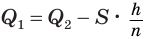 , где
, где 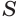 — площадь основания пирамиды. Теперь учтем, что
— площадь основания пирамиды. Теперь учтем, что 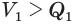 , a
, a 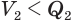 . Поэтому
. Поэтому 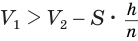 , или
, или 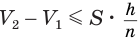 . При увеличении значения переменной
. При увеличении значения переменной 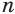 значение выражения
значение выражения 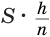 стремится к нулю, а это означает, что
стремится к нулю, а это означает, что 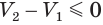 , или
, или

Такие же рассуждения можно провести, если первую и вторую пирамиды поменять ролями. В результате получим неравенство

Из неравенств (1) и (2) следует, что 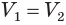 .
.
Теорема 4.
Объем пирамиды равен третьей доле произведения площади ее основания и высоты:
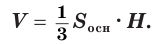
Доказательство:
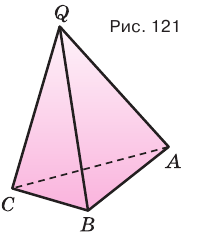
Пусть есть треугольная пирамида  (рис. 121). Достроим ее до призмы
(рис. 121). Достроим ее до призмы  с основанием
с основанием 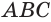 (рис. 122). Отделим от призмы данную пирамиду, получится четырехугольная пирамида
(рис. 122). Отделим от призмы данную пирамиду, получится четырехугольная пирамида 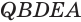 (рис. 122 и 123). Диагональная плоскость
(рис. 122 и 123). Диагональная плоскость 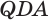 разделяет ее на две пирамиды
разделяет ее на две пирамиды  и
и  , у которых одна и та же высота, проведенная из вершины
, у которых одна и та же высота, проведенная из вершины 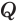 , и равные основания
, и равные основания 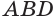 и
и 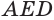 . Поэтому, в соответствии с теоремой 3, пирамиды
. Поэтому, в соответствии с теоремой 3, пирамиды  и
и  равновелики. Сравним пирамиду
равновелики. Сравним пирамиду  с данной пирамидой
с данной пирамидой  . У них равные основания
. У них равные основания 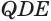 и
и  и высоты, проведенные из вершин
и высоты, проведенные из вершин 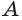 и
и 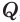 , поэтому эти пирамиды также равновелики. Получается, что все три пирамиды
, поэтому эти пирамиды также равновелики. Получается, что все три пирамиды  ,
,  и
и  равновелики. Поскольку объем призмы
равновелики. Поскольку объем призмы  равен произведению
равен произведению  площади
площади 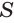 основания
основания  и высоты призмы
и высоты призмы 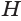 , которая равна высоте пирамиды
, которая равна высоте пирамиды  , то объем пирамиды
, то объем пирамиды  , т. е. третьей части призмы
, т. е. третьей части призмы  , равен третьей доле этого объема, т. е.
, равен третьей доле этого объема, т. е. 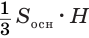 .
.
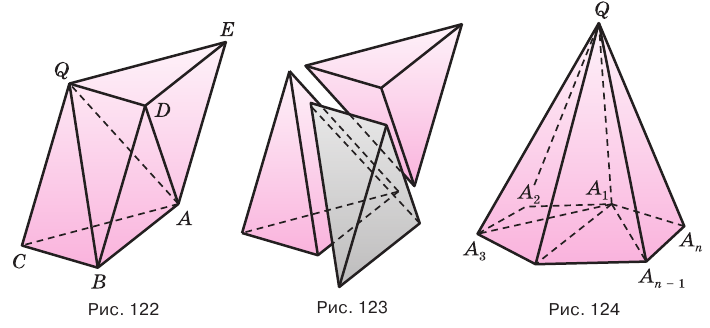
Пусть теперь есть произвольная пирамида 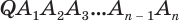 (рис. 124). Через диагонали
(рис. 124). Через диагонали 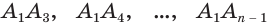 основания
основания 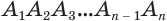 , выходящие из одной вершины
, выходящие из одной вершины 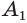 , проведем диагональные сечения, они разделят данную пирамиду на треугольные пирамиды
, проведем диагональные сечения, они разделят данную пирамиду на треугольные пирамиды 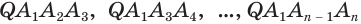 . Поскольку все они имеют общую высоту
. Поскольку все они имеют общую высоту  , то
, то
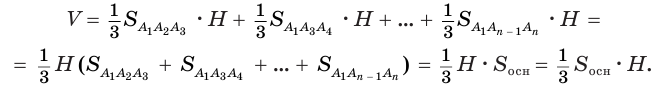
Пример:
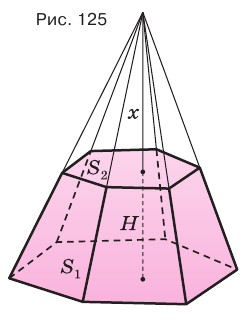
Найдем объем усеченной пирамиды, нижнее и верхнее основания которой имеют площади 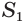 и
и 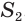 , а высота равна
, а высота равна  (рис. 125).
(рис. 125).
Для этого достроим данную усеченную пирамиду до полной. Пусть высота дополнительной пирамиды равна 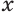 . Искомый объем
. Искомый объем 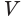 можно найти как разность объемов полной и дополнительной пирамид:
можно найти как разность объемов полной и дополнительной пирамид:
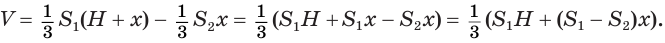
Чтобы найти высоту 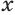 , используем установленное в теореме 1 утверждение о том, что площади сечений пирамиды относятся как квадраты их расстояний от вершины:
, используем установленное в теореме 1 утверждение о том, что площади сечений пирамиды относятся как квадраты их расстояний от вершины:
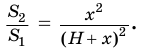
Решим это уравнение, учитывая, что  и
и  — положительные числа:
— положительные числа:
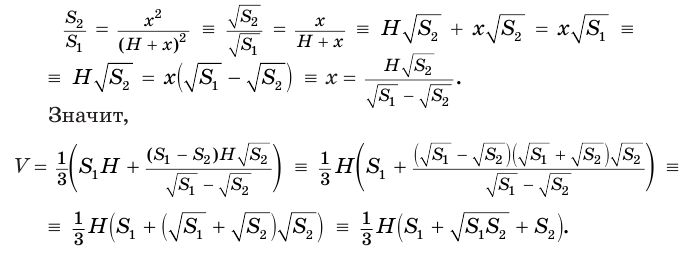
Таким образом, объем 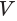 усеченной пирамиды равен третьей доле произведения высоты
усеченной пирамиды равен третьей доле произведения высоты 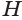 пирамиды и суммы площадей
пирамиды и суммы площадей  и
и  оснований пирамиды и их среднего геометрического
оснований пирамиды и их среднего геометрического 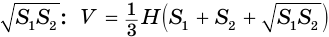 .
.
- Конус в геометрии
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Возникновение геометрии
- Призма в геометрии
- Цилиндр в геометрии
- Стереометрия – формулы, определение и вычисление
Главная » Образование » Школа » Как найти высоту в пирамиде: треугольной, четырехугольной, правильной
Как найти высоту в пирамиде: треугольной, четырехугольной, правильной
![]()
33774 Просмотров 0

Высота основания в пирамиде – тема, на которую часто попадаются задачи на экзаменах и в старших классах. Решать такие задачи просто, если понимать принцип решения и знать формулы.
В нашей статье, вы без лишних формул и теории сможете понять, как решать задачи на нахождение высоты в пирамиде. Обратите внимание, что в разделе «формулы» отсутствуют все формулы правильной пирамиды, так как наша цель – научить решать задачи на нахождение высоты.
Содержание этой статьи:
- Теория
- Часто задаваемые вопросы
- Типичные ошибки на ЕГЭ
- Полезные советы
Теория
Это интересно: Как оформлять реферат в школе по ГОСТу + образец титульного листа 2019
Правильная пирамида
Правильная пирамида имеет в основании многоугольник, а высота проходит через центр основания. Боковые грани – равнобедренные треугольники. Напомним, что в равнобедренном треугольнике две стороны равны, следовательно, боковые ребра в правильной пирамиде тоже равны. Многоугольник в основании правильный, т.е. его стороны равны.
Для решения задач понадобится знать теоремы равнобедренного треугольника:
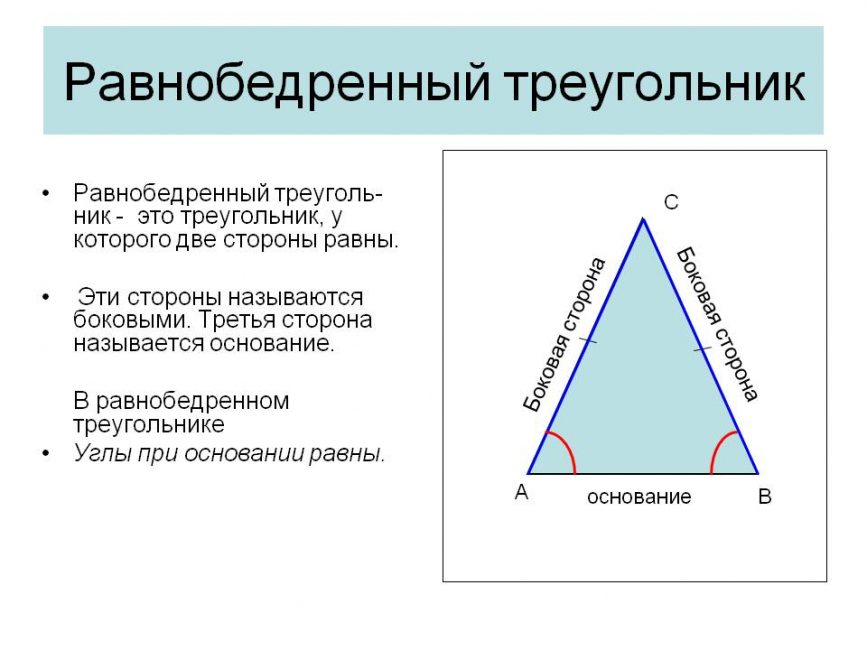
Равнобедренный треугольник
Основные свойства
1В правильную пирамиду можно вписать и описать сферу, так как при пересечении диагоналей, основание делится на равные части. Сферу нельзя вписать в любую фигуру.
2Площадь боковой поверхности – половина произведения периметра основания на апофему. Апофема есть на каждой грани, а не только на одной.
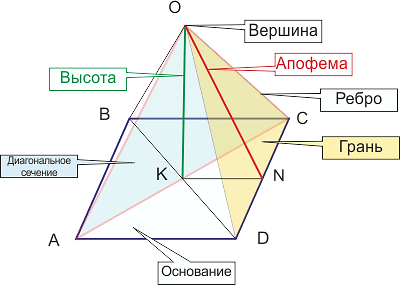
Пирамида
Четырехугольная пирамида
В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.

Четырехугольная пирамида
Треугольная пирамида
Читайте также: Как решать задачи по математике 5 класс
В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.
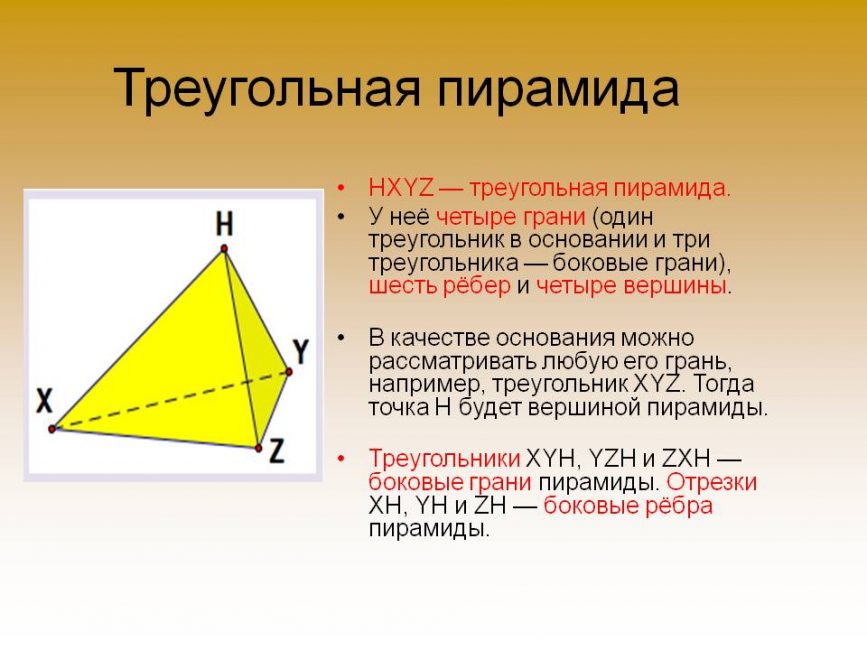
Треугольная пирамида
Необходимые знания для нахождения высоты
1Нужно понимать, что из себя представляют треугольники: свойства, формулы, определение. Большинство задач решается через треугольники (боковые грани).
2Понимать, что такое сечение и как оно влияет на геометрическую фигуру.
3Что такое правильные многоугольники: виды, свойства, формулы.
Когда теория закреплена, можно переходить к формулам.
Формулы для нахождения высоты
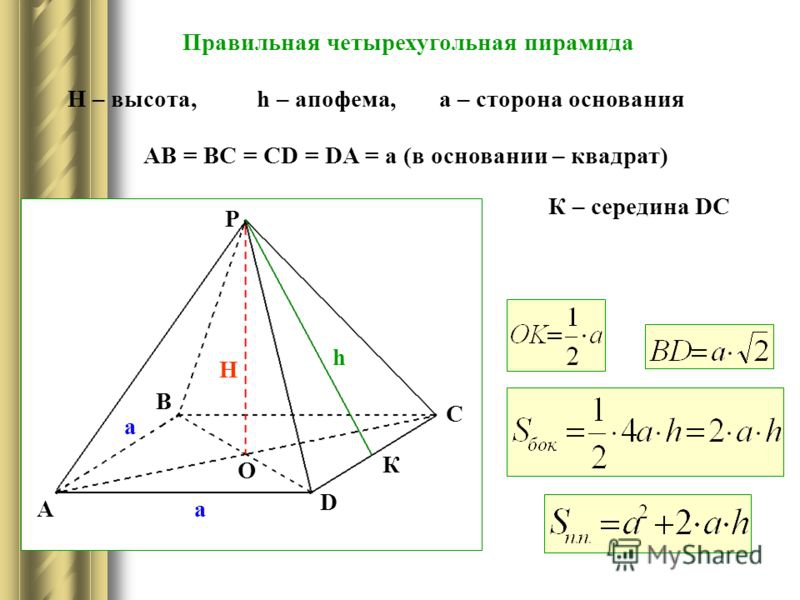
Формулы
Запомните, что маленькая буква h – это апофема, а большая H – высота.
В некоторых задачах, высоту можно найти через объем:
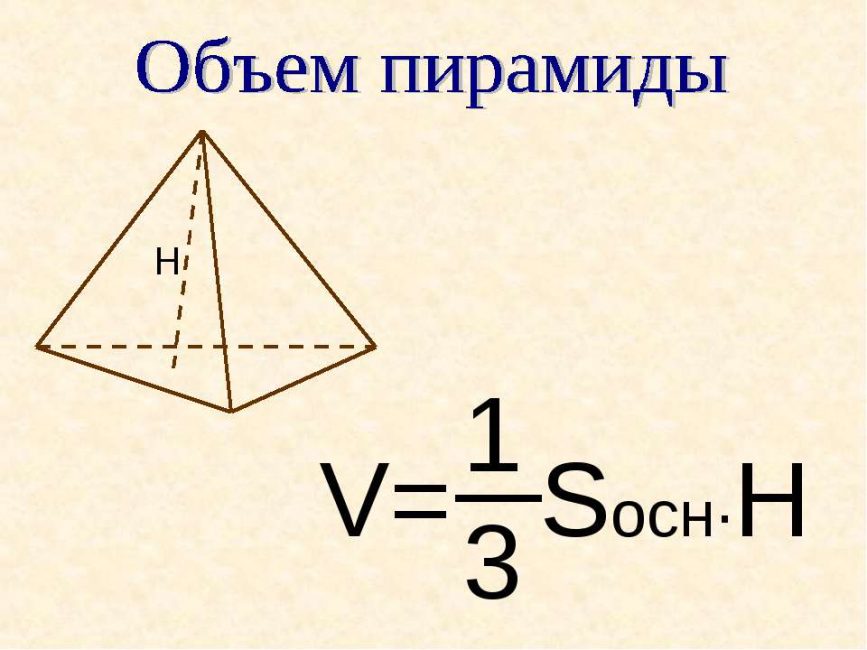
Объем пирамиды
ВИДЕО: Примеры решения задач
Нахождение высоты в правильной пирамиде
Нахождение высоты в правильной пирамиде
Ниже будут представлены текстовые решения часто встречающихся задач.
Треугольная пирамида
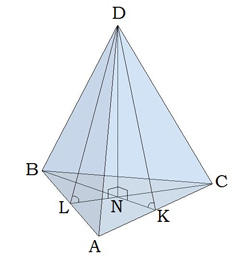
Треугольная пирамида
Задача 1
В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.
DN – высота, следовательно, объем фигуры можно выразить по формуле:
DN = 3V/S основания = 3*12/4 = 9
Ответ: 9
Задача 2
DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.
Пользуясь формулой объема, получается:
DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6
Ответ: 6
Четырехугольная пирамида
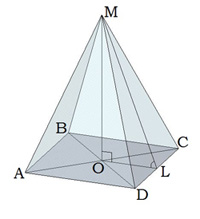
Четырехугольная пирамида
Задача 1
Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.
ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:
OL = ½*12 = 6
Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:
MO ² = √ML ² — √OL ² = √100- √36 = √64
MO = 8
Задача 2
Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.
Найдем OL
В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).
Пользуясь теоремой Пифагора, находим OL:
OL² = √OC² — √LC² = √100 – √36 = √64 = 8
Задача 3
Ищем MO
Пользуясь той же теоремой, находим высоту:
MO² = √ML² – √OL² = 100 – 64 = 36
Ответ: 36
Задача 4
Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.
Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.
Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема. Пользуясь формулами, найдем высоту.
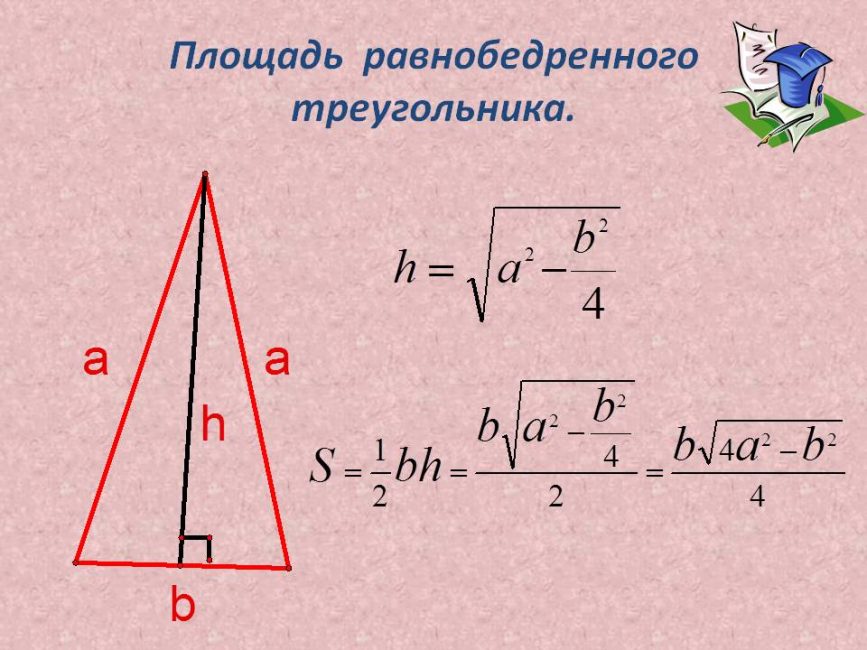
Площадь равнобедренного треугольника
36 = ½ * 4 *h
36 = 2h
H = 18
Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.
MO = ML – OL = 18 – 6 = 12
Ответ: 12
Часто задаваемые вопросы
1Как понять, что пирамида правильная, если в условии это не указано?
Часто в задании не указывают какой тип фигуры, чтобы человек сам догадался и применил нужные формулы. Понять какой тип фигуры легко – начните решение задачи с рассмотрения основания и заучивания свойств фигуры.
Зная определения и свойства, определить тип фигуры очень легко.
2Могут ли быть указаны в задании лишние данные?
Чтобы решать задачи, человек должен включать логику, а не подставлять исходные числа в знакомые формулы. С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.
3Обязательно ли оформлять высоту большой буквой H? Нужно ли выделять апофему?
Для удобства, человек может не выделять отдельно высоту, а сразу писать, например, BE (если B – вершина, а E – основание). То же с апофемой. Важно, чтобы сам человек осознавал, что это за линия и как ее использовать в решении.
4Как можно быстро изучить стереометрию?
Ключ к пониманию стереометрии – умение визуализировать объекты в пространстве. Если в дополнение к этому умению, знать формулы, свойства и теорию – задачи будут решаться быстро и безошибочно.
4Как искать высоту, если известен объем?
Если выразить высоту через формулу объема, то получится следующее:
H = (3*V)/ S;
Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²
H = 3*70/30 = 7см
Типичные ошибки на ЕГЭ
Незнание темы
Когда человек не знает, где находится апофема и что для нее есть определенные формулы, задачу может и можно решить, но тогда необходимо выполнить в 2 раза большей действий.То же обстоит с теорией – если человек не знает свойства многоугольников, то и решить задание он не сможет. Для того, чтобы понимать геометрию, не нужно обладать особенными способностями. Даже при отсутствии способностей к математике, зная теорию, вы будете понимать геометрию.
Отсутствие проверки
Хотите потерять балл на ЕГЭ? – не перепроверяйте решения. Часто, задания решаются хаотично и на листе бумаге разные решения намешаны в кучу. Когда приходит время написать ответ, человек по невнимательности либо забывает выполнить последнее действие, либо вписывает не тот ответ.Решайте задачи по действиям, проставляйте пункты и делайте проверку ответа, каким бы он ни был.
Задачи под копирку
Решая сотни аналогичных задач, человек настолько привыкает, что теряет бдительность, игнорируя многие исходные данные. Придя на экзамен, в задании может быть вопрос с подвохом и человек ошибается в теме, которую он знал идеально. Помните, к каждой задаче нужен индивидуальный подход, как бы хорошо вы в ней не разбирались.
Запись
Структурируйте решения, прописывая каждое действие и каждый полученный вывод. Это необходимо для того, чтобы не запутаться. Решая задания хаотично, можно легко записать неправильное число, не тот ответ, подставить не те числа, и задача уже решена неверно. Обидно получать низкий балл из-за невнимательности.
Подсчеты в уме
На экзамене все нервничают и переживают, а потому зарабатывают баллы ниже, чем планировалось изначально. Когда человек нервничает, уровень концентрации и внимания резко снижается. Он может упустить что-то важное, не поставить запятую или запутаться в ходе размышлений.Считая примеры в столбик, вы обезопасите себя от глупых ошибок.
Незнание структуры экзамена
Очень обидные ошибки допускают люди, пересдающие ЕГЭ через несколько лет, либо обучающиеся в экстернате. Как правило, они плохо знакомы с процедурой заполнения бланков и внесения ответов.Заполнение бланков для части А и С – различно. Внимательно посмотрите, как необходимо их заполнять, так как неправильное внесение ответа (например, запятая и число в одной клетке) будет приравниваться к ошибке и ответ будет не засчитан.Также, если вы самостоятельно готовитесь к экзамену, учитесь рассчитывать время на каждое задание.
Поспешные решения
В случае, если ответ был записан с ошибкой, его можно внести в графе ниже, заменив неправильный ответ на правильный. Однако, клетки для внесения результатов ограничены в количестве, а заданий в общей сложности 19!Несколько раз перепроверьте ответы, прежде чем внести их в бланк ответов.
Незнание степеней числа
В теореме Пифагора будут использованы не только маленькие числа (до 10). В профильной математике, могут быть крупные числа, которые тяжело посчитать в столбик.Также, степени числа могут понадобиться для других заданий. Выучите значение чисел в квадрате и кубе от 1 до 20. Помните, что на профильном экзамене, пользовать методической таблицей нельзя!
Полезные советы
- Если в задаче указан объем – ищите высоту через него.
- Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
- Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
- Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.
- Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.
6.5 Total Score
Чтобы успешно решить задачу для нахождения высоты пирамиды, достаточно знать теорию и формулы. Добавив к своим знаниям немного практики и внимательности, вы легко и быстро будете решать подобные задачи!
Если вы не согласны с рейтингом статьи, то просто поставьте свои оценки и аргументируйте их в комментариях. Ваше мнение очень важно для наших читателей. Спасибо!
Достоверность информации
8.5
Актуальность информации
7.5
ПЛЮСЫ
- Благодаря доступной информации можно легко научиться решать задачи по геометрии
МИНУСЫ
- Необходимы знания математики
Добавить отзыв
Как найти высоту в правильной пирамиде
Пирамида представляет собой многогранник, в основании которого лежит многоугольник, а грани его представляют собой треугольники, обладающие общей вершиной. Для правильной пирамиды справедливо то же определение, но в основании ее лежит правильный многоугольник. Под высотой пирамиды подразумевается отрезок, который проведен от вершины пирамиды к основанию, и этот отрезок перпендикулярен ему. Найти высоту в правильной пирамиде очень легко.
Вам понадобится
- В зависимости от ситуации, знать объем пирамиды, площадь боковых граней пирамиды, длину ребра, длину диаметра многоугольника в основании.
Инструкция
Одним из способов найти высоту пирамиды, и не только правильной – это выразить ее через объем пирамиды. Формула, с помощью которой можно узнать ее объем, выглядит так:
V = (S*h)/3, где S – площадь всех боковых граней пирамиды в сумме, h – высота данной пирамиды.
Тогда из этой формулы можно вывести другую, для нахождения высоты пирамиды:
h = (3*V)/S
К примеру, известно, что площадь боковых граней пирамиды 84 см², а объем пирамиды равен 336 куб.см. Тогда найти высоту можно так:
h = (3*336)/84 = 12 см
Ответ: высота данной пирамиды 12 см
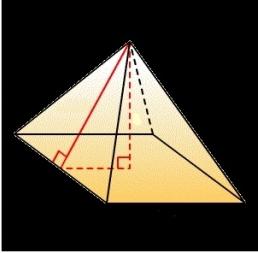
Рассматривая правильную пирамиду, в основании которой лежит правильный многоугольник, можно прийти к выводу, что треугольник, образованный высотой, половиной диагонали и одной из граней пирамиды, представляет из себя прямоугольный треугольник (например, это треугольник АEG на рисунке выше). Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов (a² = b² + c²). В случае с правильной пирамидой, гипотенуза – это грань пирамиды, один из катетов – половина диагонали многоугольника в основании, а другой катет – высота пирамиды. В таком случае, зная длину грани и диагонали, можно вычислить и высоту. В качестве примера можно рассмотреть треугольник AEG:
AE² = EG²+GA²
Отсюда высоту пирамиды GA можно выразить так:
GA = √(AE²-EG²).
Чтобы было более понятно, как находить высоту правильной пирамиды, можно рассмотреть пример: в правильной пирамиде длина грани 12 см, длина диагонали многоугольника в основании – 8 см. Исходя из этих данных, требуется найти длину высоты этой пирамиды.Решение: 12² = 4² + c², где с – неизвестный катет (высота) данной пирамиды (прямоугольного треугольника).
144 = 16 + 128
Таким образом, высота данной пирамиды √128 или, приблизительно, 11.3 см
Источники:
- правильная четырехугольная пирамида найти высоту
- Решение заданий С2 ЕГЭ по математике
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Пирамида – это многогранник, в основании которого лежит многоугольник. Все грани в свою очередь образуют треугольники, которые сходятся в одной вершине. Пирамиды бывают треугольными, четырехугольными и так далее. Для того чтобы определить, какая пирамида перед вами, достаточно посчитать количество углов в ее основании. Определение “высота пирамиды” очень часто встречается в задачах по геометрии в школьной программе. В статье попробуем рассмотреть разные способы ее нахождения.
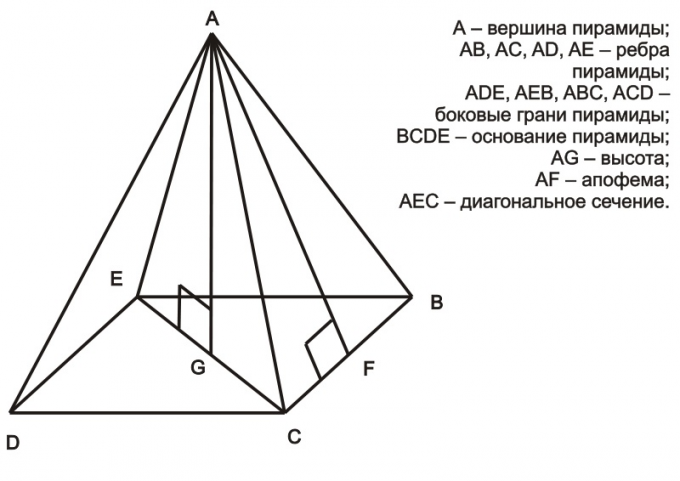
Части пирамиды
Каждая пирамида состоит из следующих элементов:
- боковые грани, которые имеют по три угла и сходятся в вершине;
- апофема представляет собой высоту, которая опускается из ее вершины;
- вершина пирамиды – это точка, которая соединяет боковые ребра, но при этом не лежит в плоскости основания;
- основание – это многоугольник, на котором не лежит вершина;
- высота пирамиды представляет собой отрезок, который пересекает вершину пирамиды и образует с ее основанием прямой угол.
Как найти высоту пирамиды, если известен ее объем
Через формулу объема пирамиды V = (S*h)/3 (в формуле V – объем, S – площадь основания, h – высота пирамиды) находим, что h = (3*V)/S. Для закрепления материала давайте сразу же решим задачу. В треугольной пирамиде площадь основания равна 50 см2, тогда как ее объем составляет 125 см3. Неизвестна высота треугольной пирамиды, которую нам и необходимо найти. Здесь все просто: вставляем данные в нашу формулу. Получаем h = (3*125)/50 = 7,5 см.
Как найти высоту пирамиды, если известна длина диагонали и ее ребра
Как мы помним, высота пирамиды образует с ее основанием прямой угол. А это значит что высота, ребро и половина диагонали вместе образуют прямоугольный треугольник. Многие, конечно же, помнят теорему Пифагора. Зная два измерения, третью величину найти будет несложно. Вспомним известную теорему a² = b² + c², где а – гипотенуза, а в нашем случае ребро пирамиды; b – первый катет или половина диагонали и с – соответственно, второй катет, или высота пирамиды. Из этой формулы c² = a² – b².
Теперь задачка: в правильной пирамиде диагональ равна 20 см, когда как длина ребра – 30 см. Необходимо найти высоту. Решаем: c² = 30² – 20² = 900-400 = 500. Отсюда с = √ 500 = около 22,4.
Как найти высоту усеченной пирамиды
Она представляет собой многоугольник, который имеет сечение параллельно ее основанию. Высота усеченной пирамиды – это отрезок, который соединяет два ее основания. Высоту можно найти у правильной пирамиды, если будут известны длины диагоналей обоих оснований, а также ребро пирамиды. Пусть диагональ большего основания равна d1, в то время как диагональ меньшего основания – d2, а ребро имеет длину – l. Чтобы найти высоту, можно с двух верхних противоположных точек диаграммы опустить высоты на ее основание. Мы видим, что у нас получились два прямоугольных треугольника, остается найти длины их катетов. Для этого из большей диагонали вычитаем меньшую и делим на 2. Так мы найдем один катет: а = (d1-d2)/2. После чего по теореме Пифагора нам остается лишь найти второй катет, который и является высотой пирамиды.
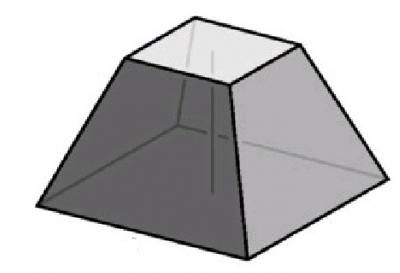
Теперь рассмотрим все это дело на практике. Перед нами задача. Усеченная пирамида имеет в основании квадрат, длина диагонали большего основания равняется 10 см, в то время как меньшего – 6 см, а ребро равняется 4 см. Требуется найти высоту. Для начала находим один катет: а = (10-6)/2 = 2 см. Один катет равен 2 см, а гипотенуза – 4 см. Получается, что второй катет или высота будет равна 16-4 = 12, то есть h = √12 = около 3,5 см.
§ 14. Пирамида
14.1. Определение пирамиды и её элементов
Определение. Пирамидой называется многогранник, у которого одна грань — многоугольник, а остальные грани — треугольники с общей вершиной (рис. 95, 96).

Рис. 95

Рис. 96
Многоугольник называется основанием пирамиды, остальные грани — боковыми гранями пирамиды, их общая вершина — вершиной пирамиды. Отрезки, соединяющие вершину пирамиды с вершинами её основания, называются боковыми рёбрами пирамиды.
Пирамиду с основанием АВСDЕ и вершиной Р обозначают PABCDE.
Перпендикуляр, опущенный из вершины пирамиды на плоскость её основания, называется высотой пирамиды. Длину этого перпендикуляра также называют высотой пирамиды.
Пирамида называется n-угольной, если её основанием является n-угольник.
На рисунке 96 изображена четырёхугольная пирамида PABCD, у которой: четырёхугольник ABCD — основание пирамиды; точка Р — вершина пирамиды; отрезки РA, РВ, PC, PD — боковые рёбра пирамиды; отрезки АВ, ВС, CD, DA — стороны (рёбра) основания пирамиды; отрезок РО — высота пирамиды; треугольники РАВ, РВС, PCD, PDA — боковые грани пирамиды.

Рис. 97
У n-угольной пирамиды имеется (n + 1) вершин, 2n рёбер и (n + 1) граней. Диагоналей пирамида не имеет. В пирамиде различают плоские углы при её вершине и двугранные углы при её рёбрах. Двугранным углом при ребре пирамиды называют содержащий пирамиду двугранный угол, образованный плоскостями граней, проходящими через данное ребро.
Треугольную пирамиду (рис. 97) называют также тетраэдром («тетраэдр» по-гречески означает «четырёхгранник»). Тетраэдр — это многогранник с наименьшим числом граней. Любая грань тетраэдра может быть принята за его основание; это отличает тетраэдр от всех остальных пирамид.
Любую пирамиду можно разбить на некоторое число тетраэдров, а любой выпуклый многогранник — на некоторое число пирамид. Для этого достаточно, например, взять любую точку внутри данного многогранника и соединить её отрезками со всеми его вершинами. Такое разбиение часто используется при нахождении объёмов многогранников.
14.2. Некоторые виды пирамид
Если все боковые рёбра пирамиды составляют с плоскостью основания равные углы, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые рёбра пирамиды равны между собой.

Рис. 98
Доказательство. а) Пусть отрезок РО — высота пирамиды PABCDEF, все рёбра которой составляют с плоскостью основания угол ϕ (рис. 98). Тогда прямоугольные треугольники РОА, POB, POC, POD, РОЕ и POF, имея общий катет РО, равны между собой (по катету и острому углу ϕ). Из равенства этих треугольников следует: ОА = OВ = ОС = OD = OE = OF, т. е. вершины основания пирамиды равноудалены от основания О её высоты РО. Это означает, что точка О — центр окружности, описанной около основания ABCDEF данной пирамиды.
б) Из ОА = OВ = ОС = OD = ОЕ = OF следует, что боковые рёбра РА, РВ, PC, PD, РЕ, PF пирамиды равны, как наклонные, имеющие равные проекции, т. е. РА = РВ = PC = PD = РЕ = PF. Что и требовалось доказать. ▼
Вы самостоятельно можете доказать обратные утверждения.
1. Если основание высоты пирамиды совпадает с центром окружности, описанной около её основания, то: а) все боковые рёбра пирамиды образуют с плоскостью основания равные углы; б) все боковые рёбра пирамиды равны между собой.
2. Если все боковые рёбра пирамиды равны, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые рёбра пирамиды составляют с плоскостью её основания равные между собой углы.
Также имеет место следующее утверждение.
Если высота пирамиды пересекает её основание и все боковые грани пирамиды образуют с плоскостью основания равные двугранные углы, то основание высоты пирамиды совпадает с центром окружности, вписанной в её основание.
Доказательство. Пусть РО — высота пирамиды PABCDE, боковые грани которой образуют с плоскостью основания пирамиды двугранные углы, равные ϕ (рис. 99).

Рис. 99
Проведём высоты РН1, РH2, РН3, PH4, РH5 боковых граней.
Тогда по теореме о трёх перпендикулярах получаем OH1 ⟂ AB, OH2 ⟂ BC, OH3 ⟂ CD, OH4 ⟂ DE, OH5 ⟂ EA, следовательно, ∠ OH1P = ∠ OH2P = ∠ OH3P = ∠ OH4P = ∠ OH5P = ϕ. Поэтому △ OH1P = △ OH2P = △ OH3P = △ OH4P = △ OH5P (как прямоугольные с общим катетом OP и острым углом ϕ). Из равенства этих треугольников следует ОН1 = OH2 = OH3 = ОН4 = ОН5, т. е. точка О — основание высоты РО пирамиды — равноудалена от всех сторон многоугольника ABCDE. Это означает, что точка O является центром окружности, вписанной в основание ABCDE данной пирамиды. Теорема доказана. ▼
Самостоятельно докажите обратное утверждение.
Если вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды, то боковые грани пирамиды образуют с плоскостью основания равные двугранные углы.
Перечислим ещё несколько часто встречающихся в задачах видов пирамид.

Рис. 100

Рис. 101

Рис. 102
• Пирамида, ровно одна боковая грань которой перпендикулярна плоскости основания. Высота такой пирамиды лежит в этой, перпендикулярной основанию, грани (рис. 100).
• Пирамида, две соседние боковые грани которой перпендикулярны плоскости основания. Высотой такой пирамиды служит боковое ребро, общее для этих граней (рис. 101).
• Пирамида, две не соседние боковые грани которой перпендикулярны плоскости основания. Высота такой пирамиды лежит на прямой пересечения плоскостей этих граней (рис. 102).
14.3. Правильная пирамида
Определение. Пирамида называется правильной, если её основание — правильный многоугольник и вершина пирамиды проектируется в центр этого основания.

Рис. 103
Из определения следует алгоритм построения изображения правильных пирамид, что, в свою очередь, доказывает существование таких пирамид.
Для построения изображения правильной пирамиды достаточно построить изображение соответствующего правильного многоугольника (основания пирамиды) и его центра. Затем из построенного центра провести перпендикуляр к плоскости многоугольника и выбрать на этом перпендикуляре (в качестве вершины пирамиды) любую точку, отличную от центра многоугольника. Соединив отрезками прямых эту точку со всеми вершинами многоугольника, получим изображение правильной пирамиды.
На рисунке 103, а, б, в построены изображения правильных пирамид: а) треугольной; б) четырёхугольной; в) шестиугольной.
Правильные пирамиды обладают замечательным свойством.
В правильной пирамиде все боковые рёбра равны, а все боковые грани — равные равнобедренные треугольники.

Рис. 104
Доказательство. Рассмотрим правильную n-угольную пирамиду РА1А2…An. Пусть точка O — центр n-угольника A1A2A3…An; отрезок РО — перпендикуляр к плоскости основания пирамиды (рис. 104).
Так как центр правильного многоугольника является центром окружности, описанной около этого многоугольника, то ОА1 = OA2 = OA3 = … = OAn (как радиусы описанной окружности). Тогда равны боковые рёбра пирамиды, как наклонные к плоскости её основания, имеющие равные проекции, т. е. PA1 = PA2 = PA3 = … = PAn.
Таким образом, имеем:
РА1 = РA2 = … = PAn (как боковые рёбра);
A1A2 = A2A3 = … = AnA1 (как стороны правильного n-угольника).
Следовательно, треугольники PA1A2, РA2A3, …, PAnA1 являются равнобедренными и по третьему признаку равенства треугольников равны между собой.
Это свойство правильной пирамиды можно доказать при помощи поворота пирамиды вокруг оси, содержащей её высоту.
Так как точка О — центр правильного n-угольника A1A2A3…An, лежащего в основании правильной пирамиды PA1A2…An, РО — перпендикуляр к плоскости её основания, то при вращении данной пирамиды вокруг оси ОР на угол, равный  (где k = 1, 2, 3, …, n), происходит самосовмещение этой пирамиды: вершины основания пирамиды отображаются на его же вершины (основание совмещается с самим собой); вершина Р (как точка оси вращения) отображается на себя. Следовательно, боковые рёбра пирамиды отображаются на боковые рёбра, а боковые грани пирамиды — на её боковые грани. А так как вращение вокруг прямой — движение, то все боковые рёбра правильной пирамиды равны между собой, а грани являются равными равнобедренными (почему?) треугольниками. Утверждение доказано. ▼
(где k = 1, 2, 3, …, n), происходит самосовмещение этой пирамиды: вершины основания пирамиды отображаются на его же вершины (основание совмещается с самим собой); вершина Р (как точка оси вращения) отображается на себя. Следовательно, боковые рёбра пирамиды отображаются на боковые рёбра, а боковые грани пирамиды — на её боковые грани. А так как вращение вокруг прямой — движение, то все боковые рёбра правильной пирамиды равны между собой, а грани являются равными равнобедренными (почему?) треугольниками. Утверждение доказано. ▼
Следствием доказанного выше является утверждение.
Все боковые рёбра правильной пирамиды образуют с плоскостью основания равные углы, а все боковые грани — равные двугранные углы.
Докажите это предложение самостоятельно.
Высота боковой грани правильной пирамиды, проведённая к ребру её основания, называется апофемой пирамиды. На рисунке 104 отрезок РН — одна из апофем пирамиды.
Все апофемы правильной пирамиды равны вследствие равенства всех её боковых граней.
Имеют место признаки правильной пирамиды:
Пирамида, в основании которой лежит правильный многоугольник, является правильной, если: а) все её боковые рёбра равны; б) все её боковые рёбра образуют с плоскостью основания равные углы; в) все её боковые грани — равные равнобедренные треугольники.
Докажите это самостоятельно.
ЗАДАЧА (2.245). Высота правильной четырёхугольной пирамиды равна h и образует с боковой гранью угол α. Через сторону основания пирамиды проведена плоскость, перпендикулярная противоположной грани и пересекающая её. Найти площадь сечения.
Дано: PABCD — правильная пирамида (рис. 105); РО — высота пирамиды, РО = h; ∠ OPF = α.
Найти: SADKM.
Решение. Первый способ. Пусть отрезок EF — средняя линия основания пирамиды. Тогда AD ⟂ EF, AD ⟂ PF ⇒ АD ⟂ (РEF) ⇒ (PEF) ⟂ (ADP) (по признаку перпендикулярности двух плоскостей). Поэтому прямая PF является ортогональной проекцией прямой РO на плоскость ADP. Значит, ∠ OPF — угол между высотой PO и боковой гранью ADP пирамиды: ∠ OPF = α.

Рис. 105
Далее имеем: AD ⟂ (PEF), ВС || AD ⇒ ВC ⟂ (PEF) ⇒ прямая ВС перпендикулярна любой прямой плоскости PEF. Поэтому если FL ⟂ РЕ (в плоскости PEF), то BС ⟂ FL. Тогда FL ⟂ ВС, FL ⟂ PE ⇒ FL ⟂ (BCP) ⇒ (ADL) ⟂ (ВCР) (по признаку перпендикулярности двух плоскостей); при этом (ADL) ∩ (ВСР) = МK, МK || AD, так как плоскости ВСР и АDL проходят через параллельные прямые ВС и AD. Значит, сечение ADKM — трапеция, у которой FL — высота (почему?), откуда
Sсеч =  •FL.
•FL.
Найдём AD, МK и FL.
В △ OPF (∠ POF = 90°):
OF = OP•tg α = h•tg α; PF =  =
=  = PE.
= PE.
Поэтому
EF = 2FO = 2h•tg α = ВС.
В плоскости PEF получаем:
FL ⟂ РЕ, РО ⟂ EF ⇒ ∠ EFL = ∠ OPE = α.
Тогда в △ ЕFL: FL = ЕF•cos α = 2h•tg α•cos α = 2hsin α;
в △ PLF (∠ PLF = 90°, ∠ PFL = 90° – 2α):
PL = PF•sin (90° – 2α) = PF•cos 2α =  .
.
Так как MK | | BC, то △ МKР ∾ △ ВСР, откуда
 =
=  ⇒ MK =
⇒ MK =  =
=  =
=
= 2htg α•cos 2α.
Таким образом,
AD = EF = 2h•tg α, FL = 2h•sin α, MK = 2h•tg α•cos 2α.
Тогда
Sсеч =  •FL =
•FL =  •2h•sin α =
•2h•sin α =
=  = 4h2•sin2 α•cos α.
= 4h2•sin2 α•cos α.

Замечание. Отрезок MK можно найти следующим образом. Сечением данной пирамиды плоскостью, проходящей через прямую MK параллельно основанию пирамиды, является квадрат MKD1A1 (см. рис. 105). F1 = A1D1 ∩ PF. У этого квадрата LF1 = MK. Найдём F1L.
В треугольнике LFF1 имеем ∠ FLF1 = α (LF1 || EF),
∠ F1FL = ∠ OFP – ∠ OFL = (90° – α) – α = 90° – 2α;
∠ FF1L = 180° – ∠ OFF1 = 90° + α. Тогда по теореме синусов

Рис. 106
Значит, MK = LF1 = 2h•tg α•cos 2α.
Второй способ. Пусть точки M1, K1, L1 — ортогональные проекции на плоскость основания соответственно точек М, K, L (рис. 105, 106). Так как плоскости АСР, BDP и EFP перпендикулярны плоскости основания пирамиды, то ортогональными проекциями прямых PC, РВ и РЕ на эту плоскость являются соответственно прямые АС, BD и EF. Следовательно, M1 ∈ BD, K1 ∈ AC, L1 ∈ EF, причём четырёхугольник ADK1M1 — равнобедренная трапеция.
Таким образом, трапеция ADK1M1 — ортогональная проекция сечения ADKM. Это означает, что SADKM =  . Найдём
. Найдём  . Так как диагонали квадрата взаимно перпендикулярны и M1K1 || AD, то OL1 = L1K1, OF = FD. Значит,
. Так как диагонали квадрата взаимно перпендикулярны и M1K1 || AD, то OL1 = L1K1, OF = FD. Значит,
 =
=  •L1F =
•L1F =  •FL1 =
•FL1 =  .
.
Тогда
SADKM =  =
=  = 4h2•sin2 α•cos α.
= 4h2•sin2 α•cos α.
Ответ: 4h2•sin2 α•cos α.
14.4.Площади боковой и полной поверхностей пирамиды
Поверхность пирамиды состоит из основания и боковых граней. В этой связи различают боковую и полную поверхности пирамиды, а также их площади.
Площадью боковой поверхности пирамиды (обозначают Sбок) называется сумма площадей всех её боковых граней: Sбок = S1 + S2 + … + Sn, где S1, S2, …, Sn — площади боковых граней пирамиды.
Площадью полной поверхности пирамиды (обозначают Sполн) называется сумма площадей всех её граней, т. е. сумма площади основания пирамиды и площади её боковой поверхности.
Из определения следует: Sполн = Sбок + Sосн.
О площади боковой поверхности правильной пирамиды имеет место следующая теорема.

Теорема 18. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему пирамиды.

Рис. 107
Доказательство. PA1A2…An — правильная пирамида, a — длина её апофемы (рис. 107).
Боковые грани правильной пирамиды — равные равнобедренные треугольники, у которых основаниями являются стороны правильного n-угольника A1A2…An, а высоты равны апофеме пирамиды, т. е.
РE1 = РE2 = PE3 = … = PEn = a.
Тогда
Sбок = S△PA1A2 + S△PA2A3 + … + S△PAnA1 =
=  A1A2•PE1 +
A1A2•PE1 +  A2A3•PE2 + … +
A2A3•PE2 + … +  An A1•PEn =
An A1•PEn =
=  a•(A1A2 + A2A3 + … + AnA1) =
a•(A1A2 + A2A3 + … + AnA1) =  P•a,
P•a,
где Р — периметр основания пирамиды. Теорема доказана. ▼

Теорема 19. Если все боковые грани пирамиды наклонены к плоскости основания под углом ϕ и высота пересекает основание, то Sбок =  .
.

Рис. 108
Доказательство. Пусть отрезок PO — высота пирамиды РA1A2A3…An, все боковые грани которой образуют с плоскостью основания углы, равные ϕ (рис. 108); отрезки PH1, PH2, …, PHn — высоты боковых граней. Тогда (по теореме о трёх перпендикулярах) OH1 ⟂ A1A2, OH2 ⟂ A2A3, …, OHn ⟂ AnA1. Значит,
∠ OH1P = ∠ OH2P = ∠ OH3P = …
… = ∠ OHnP = ϕ.
Так как точка О является центром круга, вписанного в основание пирамиды (почему?), то эта точка лежит внутри n-угольника A1A2A3…An. Поэтому n-угольник A1A2…An является объединением непересекающихся треугольников A1OA2, A2OA3, …, AnOA1. Эти треугольники являются ортогональными проекциями на плоскость основания пирамиды её соответствующих боковых граней. По теореме о площади ортогональной проекции многоугольника имеем:
S△ A1OA2 = S△ A1PA2•cos ϕ,
S△ A2OA3 = S△ A2PA3•cos ϕ,
…………………………….
S△ AnOA1 = S△ AnPA1•cos ϕ.
Сложив почленно эти равенства, получим Sосн = Sбок•cos ϕ, откуда Sбок =  . Теорема доказана. ▼
. Теорема доказана. ▼
Так как все боковые грани правильной пирамиды образуют с плоскостью основания равные двугранные углы (пусть величина этих углов равна ϕ, см. рис. 107), то для площади боковой поверхности и площади основания правильной пирамиды также справедлива формула
Sбок =  .
.
14.5. Свойства параллельных сечений пирамиды
Если плоскость α параллельна основанию пирамиды и пересекает её, то в сечении пирамиды получается некоторый многоугольник (рис. 109).

Теорема 20. Если пирамида пересечена плоскостью, параллельной основанию, то: 1) боковые рёбра и высота делятся этой плоскостью на пропорциональные части; 2) в сечении получается многоугольник, подобный основанию; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Доказательство. 1) Пусть сечением пирамиды PABCD плоскостью α, параллельной плоскости β её основания, является четырёхугольник A1B1C1D1 (см. рис. 109).

Рис. 109
Проведём высоту РО данной пирамиды и обозначим O1 = РО ∩ α.
Рассмотрим гомотетию  с центром Р, при которой плоскость основания данной пирамиды отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).
с центром Р, при которой плоскость основания данной пирамиды отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия  отображает основание ABCD пирамиды на её параллельное сечение — многоугольник А1В1С1D1, при этом вершины А, В, С, D основания пирамиды — на вершины соответственно A1, B1, C1, D1, а точку O — на точку O1 (почему?).
отображает основание ABCD пирамиды на её параллельное сечение — многоугольник А1В1С1D1, при этом вершины А, В, С, D основания пирамиды — на вершины соответственно A1, B1, C1, D1, а точку O — на точку O1 (почему?).
Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:
 =
=  =
=  =
=  =
=  = k, (*)
= k, (*)
где k — коэффициент гомотетии  . Это означает, что параллельное сечение пирамиды делит её рёбра и высоту на пропорциональные части. А поскольку гомотетия является подобием, то многоугольник A1B1C1D1, являющийся параллельным сечением пирамиды, подобен её основанию ABCD.
. Это означает, что параллельное сечение пирамиды делит её рёбра и высоту на пропорциональные части. А поскольку гомотетия является подобием, то многоугольник A1B1C1D1, являющийся параллельным сечением пирамиды, подобен её основанию ABCD.
Вследствие того, что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии, а k = РO1 : РО, где РO1 и РО — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
SA1B1C1D1 : SABCD = k2 =  : PO2.
: PO2.
Теорема доказана. ▼


Следствие. Плоскость, параллельная основанию пирамиды и пересекающая её, отсекает пирамиду, подобную данной.
14.6. Усечённая пирамида
Плоскость α, параллельная основанию пирамиды PABCD и пересекающая её, делит эту пирамиду на два многогранника: пирамиду РA1B1C1D1 и многогранник ABCDA1B1C1D1 (см. рис. 109).

Рис. 110
Многогранник ABCDA1B1C1D1 (рис. 110) называют усечённой пирамидой. Грани ABCD и A1B1C1D1, лежащие в параллельных плоскостях, называются соответственно нижним и верхним основаниями усечённой пирамиды, остальные грани — её боковыми гранями. Так как нижнее и верхнее основания усечённой пирамиды гомотетичны (т. 20), то все её боковые грани — трапеции.
Таким образом, усечённой пирамидой называется часть полной пирамиды, заключённая между её основанием и параллельным ему сечением.
У n-угольной усечённой пирамиды 2n вершин, 3n рёбер, (n + 2) грани и n(n – 3) диагоналей.
Высотой усечённой пирамиды называется перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённой пирамиды. На рисунке 110 отрезки О1О, B1K — высоты усечённой пирамиды.

Рис. 111
Усечённая пирамида называется правильной, если она получена из правильной пирамиды (рис. 111).
Из теоремы 20 следует, что основания правильной усечённой пирамиды — подобные правильные многоугольники, а боковые грани — равные равнобедренные трапеции.
Высоты этих трапеций, соединяющие середины их оснований, называются апофемами усечённой пирамиды. Все её апофемы равны между собой.
Отрезок OO1, соединяющий центры оснований правильной усечённой пирамиды, является её высотой.
Площадью боковой поверхности усечённой пирамиды называется сумма площадей всех её боковых граней.
Для правильной усечённой пирамиды имеет место

Теорема 21. Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров её оснований на апофему.
Для доказательства теоремы достаточно площадь одной из боковых граней пирамиды умножить на их число. В результате получим формулу Sбок =  •h, где Р1, P2 — периметры нижнего и верхнего оснований усечённой пирамиды, h — её апофема.
•h, где Р1, P2 — периметры нижнего и верхнего оснований усечённой пирамиды, h — её апофема.
Проведите доказательство теоремы самостоятельно.
Полная поверхность усечённой пирамиды — это объединение её оснований и боковой поверхности, поэтому для усечённой пирамиды
Sполн = Sбок + S1 + S2,
где S1 и S2 — площади большего и меньшего оснований этой пирамиды.
Для усечённой пирамиды, у которой все двугранные углы при рёбрах большего основания равны ϕ, справедливо: Sбок =  . (Для вывода этой формулы достаточно учесть следующий факт: если R и r — радиусы окружностей, вписанных соответственно в большее и меньшее основания данной пирамиды, то S1 = 0,5•P1•R, S2 = 0,5•P2•r, cos ϕ =
. (Для вывода этой формулы достаточно учесть следующий факт: если R и r — радиусы окружностей, вписанных соответственно в большее и меньшее основания данной пирамиды, то S1 = 0,5•P1•R, S2 = 0,5•P2•r, cos ϕ =  , где h — высота боковой грани этой пирамиды.)
, где h — высота боковой грани этой пирамиды.)
14.7. Объём пирамиды

Лемма. Две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики.
Доказательство. Пусть пирамиды РАВС и P1A1B1C1 имеют высоты, равные H, и равновеликие основания с площадью S; их объёмы — соответственно V1 и V2. Докажем, что V1 = V2.
Расположим пирамиды РАВС и P1A1B1C1 так, чтобы их основания лежали в одной плоскости, а сами пирамиды были расположены по одну сторону от этой плоскости (рис. 112). Тогда любая плоскость, параллельная плоскости оснований и пересекающая первую пирамиду, пересекает и вторую, причём по теореме о параллельных сечениях пирамиды площади этих сечений равны. Следовательно, на основании принципа Кавальери равны и объёмы этих пирамид. Лемма доказана. ▼

Рис. 112

Теорема 22. Объём любой треугольной пирамиды равен одной трети произведения площади основания на высоту.

Рис. 113
Доказательство. Пусть А1AВC — данная треугольная пирамида с вершиной A1 и основанием ABC (рис. 113). Дополним эту пирамиду до треугольной призмы ABCA1B1C1 с тем же основанием, одним из боковых рёбер которой является боковое ребро АA1 данной пирамиды. Это означает, что высота призмы равна высоте данной пирамиды.
Призма АВCA1B1C1 является объединением трёх треугольных пирамид с общей вершиной A1: A1ABC, A1BB1C1 и A1BCC1. Основания BB1C1 и BCC1 пирамид A1BB1C1 и A1BCC1 равны, а высота у них общая. Значит, по лемме эти пирамиды имеют равные объёмы.
Будем считать точку В вершиной пирамиды A1BB1C1, a △ A1B1C1 — её основанием. Тогда эта пирамида равновелика пирамиде А1AВС, так как у них общая высота, а основания АВС и A1B1C1 равновелики (как основания призмы). Таким образом, призма ABCA1B1C1 является объединением трёх равновеликих пирамид, одной из которых является данная пирамида A1ABC. Это означает, что объём V пирамиды A1АВС составляет одну треть объёма призмы ABCA1B1C1, т. е. V =  Socн•Н, где Н — длина высоты призмы. Но построенная призма и данная пирамида имеют общую высоту, длина которой равна Н, следовательно, объём треугольной пирамиды вычисляется по формуле
Socн•Н, где Н — длина высоты призмы. Но построенная призма и данная пирамида имеют общую высоту, длина которой равна Н, следовательно, объём треугольной пирамиды вычисляется по формуле
V =  Sосн•H,
Sосн•H,
где Н — длина высоты данной пирамиды. Теорема доказана. ▼

Рис. 114
На рисунке 114 изображены треугольная призма ABCDEF и составляющие её три равновеликие треугольные пирамиды ABDF, ABCF и BDEF.

Рис. 115
Для вычисления объёма n-угольной пирамиды PA1A2…An (рис. 115) разобьём её основание A1A2…An диагоналями A1A3, A1A4, …, A1An – 1 на треугольники с общей вершиной A1. Тогда данная пирамида разбивается в объединение пирамид PA1A2A3, PA1A3A4, …, PA1An – 1An с общей вершиной Р и общей высотой, которая равна высоте данной пирамиды. Основаниями этих пирамид являются треугольники разбиения основания данной пирамиды. Это означает (свойство 2 объёмов), что объём V пирамиды PA1A2…An равен сумме объёмов V1, V2, …, Vn – 2 треугольных пирамид соответственно PA1A2A3, PA1A3A4, …, PA1An – 1An.
Пусть длина высоты пирамиды равна Н, площадь её основания — S, а площади треугольников разбиения этого основания равны S1, S2, …, Sn – 2. Это означает, что S1 + S2 + … + Sn – 2 = S. Тогда получаем:
V = V1 + V2 + … + Vn – 2 =  H(S1 + S2 + … + Sn – 2) =
H(S1 + S2 + … + Sn – 2) =  S•H.
S•H.
Таким образом, объём любой пирамиды вычисляется по формуле
V =  Sосн•H,
Sосн•H,
где Sосн — площадь основания, Н — длина высоты пирамиды.

Итак, доказана теорема.


Теорема 23. Объём любой пирамиды равен одной трети произведения площади основания на высоту. ▼
14.8. Об объёме тетраэдра
У тетраэдра за основание можно принять любую его грань, на каждую из которых можно провести высоту тетраэдра из вершины, противоположной этой грани. Поэтому для объёма V одного и того же тетраэдра имеют место соотношения
V =  S1•h1 =
S1•h1 =  S2•h2 =
S2•h2 =  S3•h3 =
S3•h3 =  S4•h4,
S4•h4,
где Sk и hk (k = 1, 2, 3, 4) — площадь грани и длина опущенной на неё высоты. Эти соотношения часто используют при решении задач.
Заметим, что не в любом тетраэдре все четыре высоты пересекаются в одной точке (для сравнения — все три высоты любого треугольника пересекаются в одной точке). Тетраэдр, все высоты которого пересекаются в одной точке, называется ортоцентрическим.
Интересен также тетраэдр (рис. 116, а), все грани которого равны. Такой тетраэдр называется равногранным. Его развёрткой является остроугольный треугольник (рис. 116, б).
Докажите самостоятельно, что в равногранном тетраэдре:
—скрещивающиеся рёбра попарно равны;
—все высоты равны;
—сумма плоских углов трёхгранного угла при каждой вершине тетраэдра равна 180°;
—двугранные углы при скрещивающихся рёбрах тетраэдра равны.

Рис. 116

Рис. 117
Не менее интересен следующий факт. Пусть дан тетраэдр A1C1BD. Проведём через каждое его ребро плоскость, параллельную скрещивающемуся с ним ребру. Проведённые шесть плоскостей при пересечении образуют некоторый параллелепипед АВСDA1В1C1D1 (рис. 117), параллельные грани ABCD и A1B1C1D1 которого содержат скрещивающиеся рёбра А1C1 и BD данного тетраэдра. Тогда расстояние между основаниями АВСD и А1В1С1D1 полученного параллелепипеда равно длине его высоты и равно расстоянию между скрещивающимися рёбрами А1C1 и BD данного тетраэдра.
Этот параллелепипед можно разбить на пять тетраэдров — данный тетраэдр A1С1ВD и ещё четыре тетраэдра: A1ABD; ВВ1A1C1; C1CBD; DD1A1C1. Объём каждого из четырёх последних тетраэдров равен одной трети высоты h параллелепипеда, умноженной на половину площади его основания ABCD, т. е. шестой части объёма V полученного параллелепипеда.
Таким образом,
где ϕ — угол между диагоналями АС и BD параллелограмма ABCD. А так как AC || A1C1, то величина угла между скрещивающимися диагоналями A1С1 и BD тетраэдра А1С1BD также равна ϕ.
Мы получили: объём тетраэдра равен одной шестой произведения длин любых двух его скрещивающихся рёбер, расстояния между ними и синуса угла между скрещивающимися прямыми, содержащими эти рёбра.
Отметим ещё несколько очевидных и менее очевидных свойств тетраэдров, связанных с их объёмами.
1. Объёмы тетраэдров с равными основаниями относятся как их высоты, опущенные на эти основания.

Рис. 118
2. Объёмы тетраэдров с равными высотами относятся как площади их оснований.
3. Объёмы тетраэдров, имеющих равные трёхгранные углы, относятся, как произведения длин рёбер, образующих эти углы.

Используя рисунок 118, вы сможете легко доказать третье утверждение.
14.9. Объём усечённой пирамиды

Теорема 24. Объём усечённой пирамиды, у которой площади оснований равны S1 и S2, а высота — Н, вычисляется по формуле
V =  H(S1 +
H(S1 +  + S2).
+ S2).

Рис. 119
Доказательство. Пусть дана усечённая пирамида (рис. 119), у которой S1 > S2, а высота OO1 = H. Дополним эту пирамиду до полной пирамиды с вершиной Р. Объём V данной усечённой пирамиды равен разности объёмов полной и дополнительной пирамид.
Если длина высоты PO1 дополнительной пирамиды равна x, то высота PO полной пирамиды равна H + x.
Выразим х через S1, S2 и Н. По теореме 20 (o площадях параллельных сечений пирамиды) имеем
S1 : S2 = (H + x)2 : x2 ⇒  :
:  = (H + x) : x ⇒
= (H + x) : x ⇒
⇒
x =  .
.
Поэтому для объёма V усечённой пирамиды находим

что и требовалось доказать. ▼
