Высота тетраэдра, формула
 |
Высота тетраэдра — равна корню квадратному из двух третьих, помноженному на длину ребра тетраэдра [ h = sqrt{frac{2}{3}} a ] (h – высота тетраэдра, a – ребро тетраэдра) |
Вывод формулы высоты тетраэдра
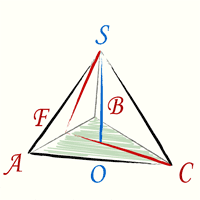
Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке
красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:
[CF = FS = frac{sqrt{3}}{2}a ; CS = a ]
Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).
[p = frac{1}{2}(a + afrac{sqrt{3}}{2} + afrac{sqrt{3}}{2}) ]
[p = frac{1}{2} a (1 + sqrt{3}) ]
[h = 2 frac{ sqrt{p(p-a)(p-(afrac{sqrt{3}}{2}))(p-(afrac{sqrt{3}}{2}))}}{afrac{sqrt{3}}{2}}]
[h = 2 frac{sqrt{(frac{a}{2})^4 (sqrt{3}+1) (sqrt{3}-1)}}{afrac{sqrt{3}}{2}} = sqrt{frac{2}{3}} a ]
Вычислить, найти высоту тетраэдра по формуле(1)
Высота тетраэдра |
стр. 283 |
|---|
Высота тетраэдра — равна корню квадратному из двух третих, помноженному на длину ребра тетраэдра
(h — высота тетраэдра, a — ребро тетраэдра)
Вывод формулы высоты тетраэдра
Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:
Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).
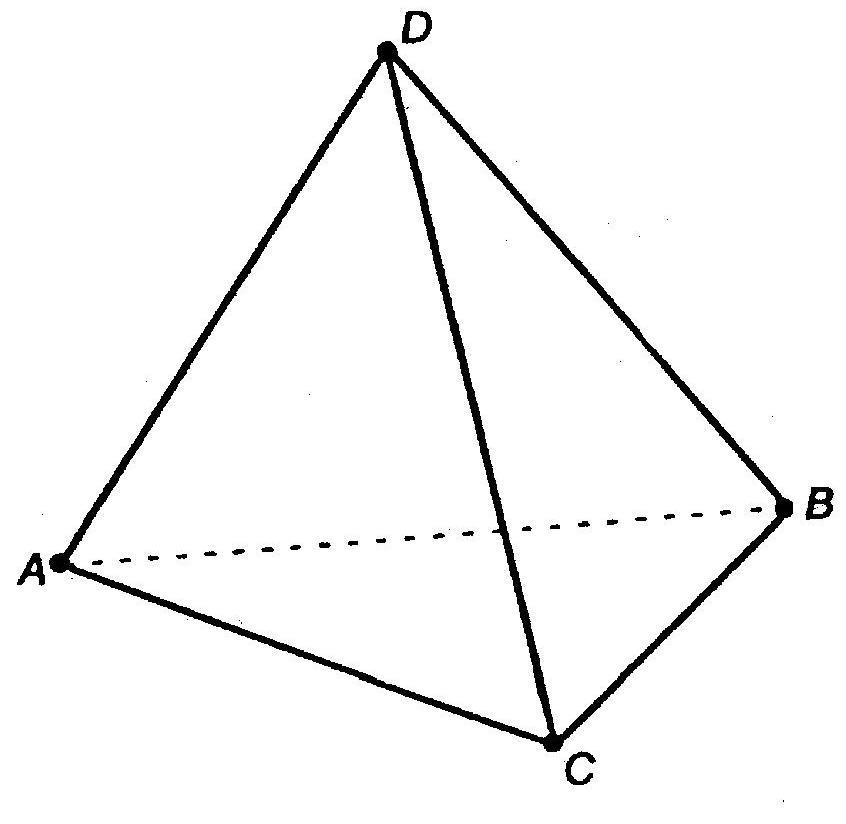
Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC . 
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра
Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.
Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле
- S – площадь любой грани,
- H – высота, опущенная на эту грань
Правильный тетраэдр – частный вид тетраэдра
Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:
- Все грани равны.
- Все плоские углы правильного тетраэдра равны 60°
- Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
- Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).
Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD .
Высота BM равна BM и равна 
Рассмотрим треугольник BDM , где DH , являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой

BM=

p=1/2 (BM+BD+DM)= 
Подставим эти значения в формулу высоты. Получим 
Вынесем 1/2a. Получим


Применим формулу разность квадратов

После небольших преобразований получим


Объем любого тетраэдра можно рассчитать по формуле 
где 

Подставив эти значения, получим
Таким образом формула объема для правильного тетраэдра
где a –ребро тетраэдра
Вычисление объема тетраэдра, если известны координаты его вершин
Пусть нам даны координаты вершин тетраэдра 
Из вершины 



Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим


Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула
Свойства
Зная высоту тетраэдра, можно вычислить его ребро, перевернув формулу так, чтобы ребро было равно корню из трех вторых, умноженному на высоту. a=√(3/2) h
Выразив таким образом ребро тетраэдра через его высоту, можно найти периметр тетраэдра, то есть длину всех его ребер, площадь одной грани и площадь полной поверхности тетраэдра. Периметр тетраэдра будет равен шести длинам его ребер, площадь одной грани – ребру в квадрате, умноженному на корень из трех, деленный на четыре, а площадь полной поверхности – четырем площадям одной грани. P=6a=6√(3/2) h S_1=(√3 a^2)/4=(3√3 h^2)/8 S_(п.п.)=4S_1=(3√3 h^2)/2
Через высоту, подставленную вместо ребра в определенном соотношении можно найти соответственно и радиусы вписанной и описанной окружностей в основание тетраэдра. r=h/(2√2) R=h/√2
Апофема тетраэдра проходит из вершины к противоположной стороне грани под прямым углом и рассчитать ее можно как из прямоугольного треугольника с боковым ребром по той же грани, так и из прямоугольного треугольника во внутреннем пространстве тетраэдра с высотой. l=3h/(2√2)
Чтобы вычислить объем тетраэдра, необходимо возвести в куб ребро и разделить полученное значение на шесть корней из двух, либо подставить вместо ребра корень из трех вторых, умноженный на высоту и преобразовать формулу объема для высоты. V=(√3 h^3)/8
В тетраэдр можно вписать сферу или описать сферу около него, тогда, зная высоту, чтобы вычислить радиусы вписанной и описанной сфер, необходимо воспользоваться следующими, уже готовыми формулами. (рис.60.2, 60.3) r_1=h/4 R_1=3h/4
Высота тетраэдра, формула
Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:
Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).
Свойства тетраэдра, виды и формулы
Тетраэдр в переводе с греческого означает «четырехгранник». Эта геометрическая фигура обладает четырьмя гранями, четырьмя вершинами и шестью ребрами. Грани представляют собой треугольники. По сути, тетраэдр — это треугольная пирамида. Первые упоминания о многогранниках появились еще задолго до существования Платона.
Сегодня поговорим об элементах и свойствах тетраэдра, а также узнаем формулы нахождения у этих элементов площади, объема и других параметров.
Элементы четырехгранника

Отрезок, выпущенный из любой вершины тетраэдра и опущенный на точку пересечения медиан грани, являющейся противоположной, называется медианой.
Высота многоугольника представляет собой нормальный отрезок, опущенный из вершины напротив.
Бимедианой называется отрезок, соединяющий центры скрещивающихся ребер.
Свойства тетраэдра
1) Параллельные плоскости, которые проходят через два скрещивающихся ребра, образуют описанный параллелепипед.
2) Отличительным свойством тетраэдра является то, что медианы и бимедианы фигуры встречаются в одной точке. Важно, что последняя делит медианы в отношении 3:1, а бимедианы — пополам.
3) Плоскость разделяет тетраэдр на две равные по объему части, если проходит через середину двух скрещивающихся ребер.
Виды тетраэдра
Видовое разнообразие фигуры достаточно широко. Тетраэдр может быть:
- правильным, то есть в основании равносторонний треугольник;
- равногранным, у которого все грани одинаковы по длине;
- ортоцентрическим, когда высоты имеют общую точку пересечения;
- прямоугольным, если плоские углы при вершине нормальные;
- соразмерным, все би высоты равны;
- каркасным, если присутствует сфера, которая касается ребер;
- инцентрическим, то есть отрезки, опущенные из вершины в центр вписанной окружности противоположной грани, имеют общую точку пересечения; эту точку именуют центром тяжести тетраэдра.
Остановимся подробно на правильном тетраэдре, свойства которого практически не отличаются.
Исходя из названия, можно понять, что так он называется потому, что грани являют собой правильные треугольники. Все ребра этой фигуры конгруэнтны по длине, а грани — по площади. Правильный тетраэдр — это один из пяти аналогичных многогранников.
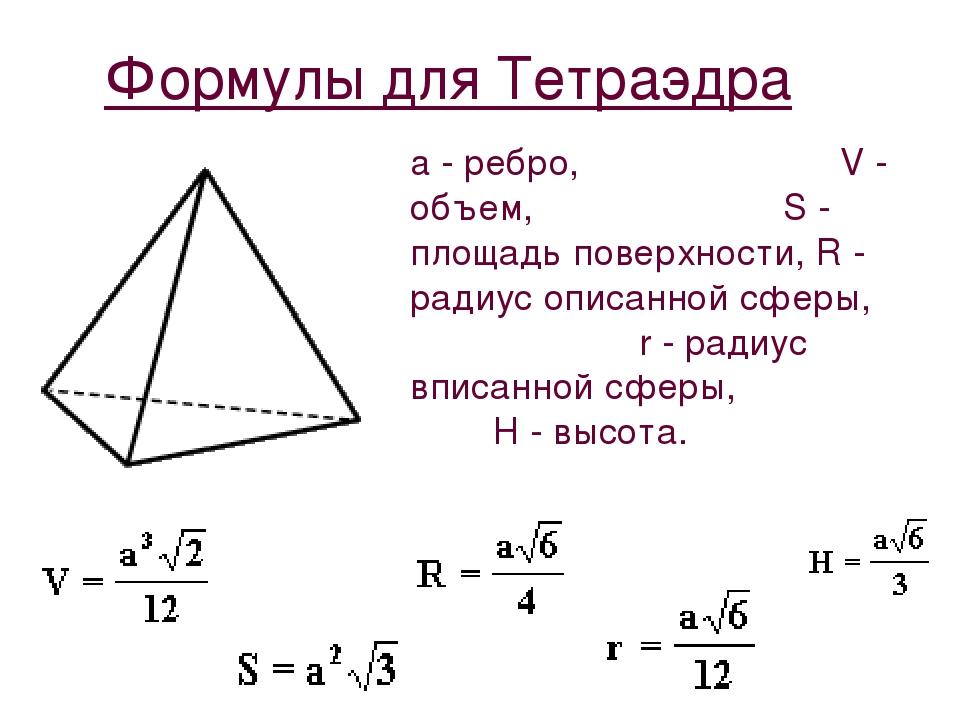
Формулы четырехгранника
Высота тетраэдра равна произведению корня из 2/3 и длины ребра.
Объем тетраэдра находится так же, как объем пирамиды: корень квадратный из 2 разделить на 12 и умножить на длину ребра в кубе.
Остальные формулы для расчета площади и радиусов окружностей представлены выше.
Как найти высоту тетраэдра
Основание можно изобразить любым треугольником ABC. Центр основания изображается точкой О пересечения медиан. (Затем две из этих медиан, как не имеющие значения для решения задачи, можно стереть, оставив только точку О на медиане АЕ).
Решение. Имеем V = 1 /3 • Socн. • Н = 1 /3 • 1 /4a 2 √ 3H . Связь между а и Н найдем из треугольника AOD, где AD = a, а АО есть радиус R, круга, описанного около основания, так что a = R√ 3 .
Подставляя a 2 = 3 /2 H 2 в выражение V, получаем V = √ 3 /8 H 3 .
I’d like to offer a slightly simpler approach to part of the 1st answer above. We know that the equilateral triangle of the base of the tetrahedron has sides of 1, 1, and 1, and we know we can split that in half, creating two right triangles having sides of hypotenuse=1, base=1/2, and perpendicular=√3/2, along with angles of 30, 60, and 90 degrees.
Now consider the 2nd diagram of the 1st answer, which shows a solid-line triangle having angles of 30, 30, and 120 degrees. That triangle could be divided in half, creating two right triangles having angles of 30, 60, and 90 degrees. If we consider the base of each triangle to be its shortest side, then the perpendicular of either one of those triangles has a length of 1/2. We can now use the power of ratios to compute the other two sides:
(1/2):(√3/2):(1) –triangle 1: half of tetrahedral face, angles of 30, 60 & 90 degrees.
( ):( 1/2):( ) –triangle 2: has unknown base & hypotenuse, but is proportionate to triangle 1.
We really only need to compute the hypotenuse of triangle 2, because that is the desired distance from the corner to the center of the tetrahedron’s base:
Multiply triangle-1-hypotenuse by triangle-2-perpendicular; divide by triangle-1-perpendicular.
[(1/2)(1)]/(√3/2) = (1/2)(2/√3) = 1/√3, as the 1st answer also computes in a more complicated way.
For the sake of completeness, since in any 30-60-90-degree triangle the base is simply half the length of the hypotenuse, the second unknown is 1/(2√3) or √3/6 (although it could also have been figured by using ratios, as above). The reader is invited to verify that the square of (√3/6) plus the square of 1/2 equals the square of (1/√3).
Как найти высоту тетраэдра
Тетраэдр является частным случаем пирамиды. Все его грани представляют собой треугольники. Кроме правильного тетраэдра, у которого все грани представляют собой равносторонние треугольники, есть еще несколько видов этого геометрического тела. Различают равногранный, прямоугольный, ортоцентрический и каркасный тетраэдры. Для того чтобы найти его высоту, нужно прежде всего определить его вид.

Вам понадобится
- – чертеж тетраэдра;
- – карандаш;
- – линейка.
Инструкция
Постройте тетраэдр с заданными параметрами. В условиях задачи должны быть даны вид тетраэдра, размеры ребер и углы между гранями. Для правильного тетраэдра достаточно знать длину ребра. Как правило, речь идет о правильных равносторонних тетраэдрах.
Повторите свойства равносторонних треугольников. У них равны все углы и составляют по 60°. Под таким же углом наклонены все грани к основанию. За основание можно принять любую сторону.
Выполните необходимые геометрические построения. Начертите тетраэдр с заданной стороной. Одну из граней его расположите строго горизонтально. Обозначьте треугольник основания как ABC, а вершину тетраэдра — как S. Из угла S проведите к основанию высоту. Точку пересечения обозначьте О. Поскольку все треугольники, из которых состоит данное геометрическое тело, равны между собой, то и высоты, проведенные из разных вершин к граням, тоже будут равны.
Из той же точки S опустите высоту и к противолежащему ребру АВ. Поставьте точку F. Это ребро является общим для равносторонних треугольников АВС и АВS. Соедините точку F с противолежащей данному ребру точкой С. Она будет одновременно являться высотой, медианой и биссектрисой угла С. Найдите равные стороны треугольника FSC. Сторона CS задана в условии и равняется a. Тогда FS=а√3/2. Эта сторона равна FC.
Найдите периметр треугольника FCS. Он равен половине суммы сторон треугольника. Подставив в формулу значения известной и найденных сторон данного треугольника, вы получите формулу p=1/2*(a+2а√3/2)=1/2a(1+√3), где а — заданная сторона тетраэдра, а p – полупериметр.
Вспомните, чему равна высота равнобедренного треугольника, проведенная к одной из его равных сторон. Вычислите высоту OF. Она равна корню квадратному из произведения полупериметра и его разностей с тремя сторонами, деленному на длину стороны FC, то есть на а*√3/2. Сделайте необходимые сокращения. В итоге у вас получится формула: высота равняется корню квадратному из двух третей, умноженному на a. H=a*√2/3.
Полезный совет
Для всех остальных видов тетраэдра также необходимо выполнить дополнительные построения, чтобы высота являлась одновременно стороной треугольника с известными вам параметрами. Вычислять ее можно разными способами, используя теорему Пифагора, теоремы синусов и косинусов. Способ определяется в зависимости от того, какими данными вы располагаете.
Источники:
- Правильная пирамида
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.