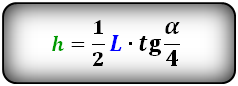Как найти высоту сегмента окружности

Как найти высоту сегмента окружности

Формула высоты сегмента круга

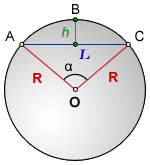
Сегмент – часть круга ABC, отсеченная хордой AC

Высота сегмента круга

h –  высота сегмента ABC

L – хорда AC

R – радиус кружности

O – центр окружности

α – центральный угол AOC

Формула высоты через радиус и центральный угол, (h):

Формула высоты сегмента круга

Формула высоты через хорду и центральный угол, (h):

Формула высоты сегмента круга

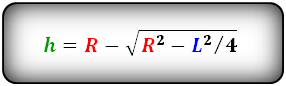
Формула высоты через радиус и хорду, (h):

Формула высоты сегмента круга

Дополнительные формулы для окружности:

Подробности

Автор: Administrator

Опубликовано: 16 октября 2011

Обновлено: 13 августа 2021

Источник

У этого термина существуют и другие значения, см. Сегмент.

Сегмент круга закрашен зелёным цветом

Сегме́нт кру́га, кругово́й сегмент — часть круга, ограниченная дугой окружности и её хордой или секущей.

Соотношения[править | править код]

Пусть R — радиус круга, c — длина хорды сегмента, s — длина дуги сегмента, h — высота сегмента, также называемая стрелкой сегмента, theta — угол дуги сегмента выраженный в радианах. Размер сегмента круга однозначно задаётся любой парой этих величин и любая величина выражается через любую другую пару. Тогда:

{displaystyle R={frac {s}{theta }}={frac {h}{1-cos {frac {theta }{2}}}}={frac {d}{cos {tfrac {theta }{2}}}}={frac {c}{2sin {tfrac {theta }{2}}}}=h+d={frac {c^{2}+4h^{2}}{8h}}={frac {1}{2}}{sqrt {4d^{2}+c^{2}}};}
{displaystyle s=theta cdot R=2Rarccos left(1-{tfrac {h}{R}}right)=2Rarccos {tfrac {d}{R}}=2Rarcsin {frac {c}{2R}}=}

{displaystyle ={frac {theta }{h}}}{1-cos {frac {theta }{2}}={frac {theta d}{cos {tfrac {theta }{2}}}}={frac {theta c}{2sin {tfrac {theta }{2}}}}=}
{displaystyle =2(h+d)arccos {tfrac {d}{h+d}}={frac {c^{2}+4h^{2}}{4h}}}arcsin {{tfrac {4hc}{c^{2}+4h^{2}}}=}
{displaystyle ={sqrt {4d^{2}+c^{2}}}}arcsin {{frac {c}{sqrt {4d^{2}+c^{2}}}};}
{displaystyle c=2Rsin {tfrac {theta }{2}}=R{sqrt {2-2cos theta }}=2{sqrt {h(2R-h)}};}
{displaystyle h=R(1-cos {tfrac {theta }{2}})=R-{sqrt {R^{2}-{tfrac {c^{2}}{4}}}};}
{displaystyle theta =2arccos {frac {d}{R}}={frac {s}{R}}=2arccos {frac {R-h}{R}}=2arcsin {frac {c}{2R}}.}

Площадь кругового сегмента вычисляется по формуле:

{displaystyle S={frac {1}{2}}R^{2}(theta -sin theta )={frac {1}{2}}R^{2}left({frac {s}{R}}-sin {tfrac {s}{R}}right).}

См. также[править | править код]

Логотип Викисловаря В Викисловаре есть статья «сегмент»
  • Сектор круга
  • Шаровой сегмент
  • Шаровой слой
  • Коническое сечение
  • Дуга окружности
  • Разрез

Формула

Это статья-заготовка по математике. Помогите Википедии, дополнив эту статью, как и любую другую.

В статье не хватает ссылок на источники (см. рекомендации по поиску).

Информация должна быть проверяема, иначе она может быть удалена. Вы можете отредактировать статью, добавив ссылки на авторитетные источники в виде сносок. (3 марта 2023)
Источник
Сегмент круга
Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
S=frac{1}{2}R^2(alpha-sin{alpha}) [1]
Длина дуги:
L={alpha}R
Длина хорды:
c=2{R}{sin{frac{alpha}{2}}}
Высота сегмента:
h={R}left(1-{cos{frac{alpha}{2}}}right)

PLANETCALC, Сегмент

Сегмент

Угол в градусах, образуемый радиусами сектора

Точность вычисления

Знаков после запятой: 2

Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

PLANETCALC, Параметры сегмента по хорде и высоте

Параметры сегмента по хорде и высоте

Точность вычисления

Знаков после запятой: 2

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
R=frac{h}{2}+frac{c^2}{8h}

Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
alpha=2arcsin{ frac{c}{2R} }
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

PLANETCALC, Площадь сегмента круга по радиусу и высоте

Площадь сегмента круга по радиусу и высоте

Точность вычисления

Знаков после запятой: 2

Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:
alpha=2arccosleft(1-frac{h}{R}right)
далее используется формула [1] для получения площади.

15 вычислений по сегменту круга в одной программе

Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:

  • длина дуги
  • угол
  • хорда
  • высота
  • радиус
  • площадь

Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.

PLANETCALC, Круговой сегмент - все варианты расчета

Круговой сегмент – все варианты расчета

Точность вычисления

Знаков после запятой: 2

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Источник

Формула высоты сегмента круга

Сегмент – часть круга ABC, отсеченная хордой AC

h – высота сегмента ABC

L – хорда AC

R – радиус кружности

O – центр окружности

α – центральный угол AOC

Формула высоты через радиус и центральный угол, ( h ):

Формула высоты через хорду и центральный угол, ( h ):

Формула высоты через радиус и хорду, ( h ):

Дополнительные формулы для окружности:

Радиус и высота сегмента круга

Свойства

Зная радиус и высоту сегмента, можно найти центральный угол α, через который становится возможным рассчитать все остальные измерения сегмента, такие как длина дуги, длина хорды и площадь сегмента круга. Из формулы высоты следует, что косинус половинного угла равен разности единицы и отношения высоты к радиусу. cos⁡〖α/2〗=1-h/r

Вычислив таким образом центральный угол сегмента круга, подставляем его в следующие формулы для длины дуги и длины хорды. Длина дуги вычисляется как произведение угла на радиус, а длина хорды находится из прямоугольного треугольника как удвоенное произведение радиуса на синус половинного угла (рис.141). P=αr c=2r sin⁡〖α/2〗

Площадь сегмента круга наряду с площадью равнобедренного треугольника, образованного двумя радиусами и хордой, является составляющей площади сектора круга. Поэтому, чтобы найти площадь сегмента необходимо вычесть из последней площадь треугольника. Упростив такое выражение, получаем половину квадрата радиуса, умноженную на разность угла α и его синуса. S=S_сек-S_тр=(r^2 α)/2-r^2 sin⁡α=1/2 r^2 (α-sin⁡α )

Длина окружности

О чем эта статья:

6 класс, 9 класс, ЕГЭ/ОГЭ

Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так – l

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Как найти длину окружности через диаметр

Хорда — это отрезок, который соединяет две точки окружности.

Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:

π— число пи — математическая константа, примерно равная 3,14

d — диаметр окружности

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

π — число пи, примерно равное 3,14

r – радиус окружности

Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

π — число пи, примерно равное 3,14

S — площадь круга

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник:

π — число пи, примерно равное 3,14

d — диагональ прямоугольника

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:

π – математическая константа, примерно равная 3,14

a – сторона квадрата

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

π — математическая константа, она примерно равна 3,14

a — первая сторона треугольника

b — вторая сторона треугольника

c — третья сторона треугольника

S — площадь треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.

Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

π — математическая константа, примерно равная 3,14

S — площадь треугольника

p — полупериметр треугольника

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.

Формула вычисления длины окружности:

π — математическая константа, примерно равная 3,14

a — сторона многоугольника

N — количество сторон многоугольника

Задачи для решения

Давайте тренироваться! Двигаемся от простого к сложному:

Задача 1. Найти длину окружности, диаметр которой равен 5 см.

Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:

Подставляем туда известные переменные и получается, что длина окружности равна

Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм

Решение. Радиус окружности равен Подставим туда наши переменные и получим

Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.

Обучение на курсах по математике поможет закрепить полученные знания на практике.

[spoiler title=”источники:”]

http://geleot.ru/education/math/geometry/calc/circular_segment/radius_and_height

http://skysmart.ru/articles/mathematic/dlina-okruzhnosti

[/spoiler]

Источник

Геометрия круга

Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..

Давайте сначала рассмотрим, какие у круга бывают части и как они называются.Круг и его части

  • Окружность — линия, ограничивающая круг.
  • Дуга — часть окружности.
  • Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
  • Хорда — отрезок, соединяющий две точки окружности.
  • Сегмент — часть круга, ограниченная хордой и дугой.
  • Сектор — часть круга, ограниченная двумя радиусами и дугой.

Интересующие нас величины и их обозначения:

Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.

  • Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
  • Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
  • Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.

Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.

Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).

И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.

И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.

1. Даны диаметр D и длина дуги L

alpha~=~L/D;     длина хорды X~=~D~*~sin alpha;
высота сегмента H~=~D~*~{1~-~cos alpha}/2;    центральный угол varphi~=~alpha~*~{360/pi}.

2. Даны диаметр D и длина хорды X

alpha~=~arcsin X/D;     длина дуги L~=~D~*~alpha;
высота сегмента H~=~D~*~{1~-~cos alpha}/2;    центральный угол varphi~=~alpha~*~ {360/pi}.

Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол alpha_1~=~pi~-~alpha.

3. Даны диаметр D и центральный угол φ

alpha~=~varphi~*~{pi/360};     длина дуги L~=~D~*~alpha;
длина хорды X~=~D~*~sin alpha;    высота сегмента H~=~D~*~{1~-~cos alpha}/2.

4. Даны диаметр D и высота сегмента H

alpha~=~arccos(1~-~{{2H}/D});     длина дуги L~=~D~*~alpha;
длина хорды X~=~D~*~sin alpha;    центральный угол varphi~=~alpha~*~{360/pi}.

6. Даны длина дуги L и центральный угол φ

alpha~=~varphi~*~{pi/360};     диаметр D~=~L/alpha;
длина хорды X~=~D~*~sin alpha;    высота сегмента H~=~D~*~{1~-~cos alpha}/2.

8. Даны длина хорды X и центральный угол φ

alpha~=~varphi~*~{pi/360};     длина дуги L~=~X~*~alpha/{sin alpha};
диаметр D~=~L/alpha;    высота сегмента H~=~D~*~{1~-~cos alpha}/2.

9. Даны длина хорды X и высота сегмента H

alpha~=~2~*~arctg~{2H}/X;     длина дуги L~=~X~*~alpha/{sin alpha};
диаметр D~=~L/alpha;    центральный угол varphi~=~alpha~*~{360/pi}.

10. Даны центральный угол φ и высота сегмента H

alpha~=~varphi~*~{pi/360};     диаметр D~=~{2 H}/{1~-~cos alpha};
длина дуги L~=~D~*~alpha;    длина хорды X~=~D~*~sin alpha.

Внимательный читатель не мог не заметить, что я пропустил два варианта:

5. Даны длина дуги L и длина хорды X
7. Даны длина дуги L и высота сегмента H

Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?

Задача эта сводится к решению уравнений:
L~*~sin alpha~=~X~*~alpha; — в варианте 5
L~*~(1~-~cos alpha)~=~2 H~*~alpha; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем Segment. Всё то, что я тут длинно рассказываю, она делает за микросекунды.

Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:

длина окружности C~=~pi~*~D;
площадь круга S~=~pi~*~D^2/4;
площадь сектора S_sect~=~S~*~{varphi/360};
площадь сегмента S_segm~=~S_sect~-~{X~*~D~*~cos alpha}/4;

И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.

Программа Segment

Источник

Добавить комментарий