В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить объем сегмента шара, а также разберем пример решения задачи для закрепления теоретического материала.
- Определение сегмента шара
-
Формулы для нахождения объема шарового сегмента
- Через радиус шара и высоту сегмента
-
Через радиус основания сегмента и его высоту
- Пример задачи
Определение сегмента шара
Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.

- R – радиус шара;
- r – радиус основания сегмента;
- h – высота сегмента; это длина перпендикуляра от центра его основания (точка O2) до точки на поверхности шара.
Формулы для нахождения объема шарового сегмента
Пояснения:
- В формулах ниже используется радиус шара (R) или радиус основания сегмента (r). Поэтому, если изначально дан их диаметр (d), то чтобы найти требуемый радиус, нужно соответствующий диаметр разделить на два.
- Число π округленно равняется до 3,14.
Через радиус шара и высоту сегмента
Чтобы найти объем (V) сегмента шара, необходимо знать радиус шара и высоту сегмента.
![]()
Через радиус основания сегмента и его высоту
Вычислить объем (V) шарового сегмента можно, зная его высоту и радиус основания (круга).
![]()
Данная формула получена следующим образом:
Радиус шара можно выразить через радиус основания сегмента и его высоту:
![]()
Таким образом, заменив R в первой формуле для расчета объема на выражение выше, получаем:
![]()
Пример задачи
Найдите объем сегмента шара, если известно, что его высота равняется 4 см, а радиус шара – 9 см.
Решение
В данном случае с учетом известных значений нам подходит первая формула:
![]()
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d2570bfec2516e3 • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.
2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности


где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:


Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:


Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Высота треугольника онлайн
С помощю этого онлайн калькулятора можно найти высоту треугольника. Для нахождения высоты треугольника введите известные элементы треугольника и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.
Открыть онлайн калькулятор
Высота треугольника. Определение
Определение 1. Отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
Высота треугольника может содержаться внутри треугольника (Рис.1), совпадать со стороной треугольника (при прямоугольном треугольнике высота совпадает с катетом (Рис.2) ), проходить вне треугольника (при тупоугольном треугольнике(Рис.3)).
Теорема о пересечении высот треугольника
Теорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.
Доказательство. Рассмотрим произвольный треугольник ABC (Рис.4). Докажем, что высоты ( small AA_1 ,) ( small BB_1 ,) ( small CC_1 ) пересекаются в одной точке. Из каждой вершины треугольника проведем прямую, параллельно противоположной стороне. Получим треугольник ( small A_2B_2C_2. ) Покажем, что точки ( small A, B, C ) являются серединами сторон треугольника ( small A_2B_2C_2. ) ( small AB=A_2C ) так как они являются противоположными сторонами параллелограмма ( small ABA_2C. ) ( small AB=CB_2 ) так как они являются противоположными сторонами параллелограмма ( small ABCB_2. ) Тогда ( small CB_2=CA_2, ) то есть точка ( small C ) является серединой стороны ( small A_2B_2 ) треугольника ( small A_2B_2C_2. ) Аналогично доказывается, что точки ( small A ) и ( small B ) являются серединами сторон ( small B_2C_2 ) и ( small A_2C_2, ) соответственно.
Далее из ( small AA_1⊥BC ) следует, что ( small AA_1⊥B_2C_2 ) поскольку ( small BC ǁ B_2C_2 ). Аналогично, ( small BB_1⊥A_2C_2, ) ( small CC_1⊥A_2B_2. ) Получили, что ( small AA_1,) ( small BB_1, ) ( small CC_1) являются серединными перпендикулярами сторон ( small B_2C_2, ) ( small A_2C_2, ) ( small A_2B_2, ) соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке.
Точка пересечения высот треугольника называется ортоцентром.
Высота треугольника по основанию и площади
Пусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).
Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:
Пример 1. Сторона треугольника равна ( small a=5 ) а площадь ( small S=7. ) Найти высоту треугольника.
Применим формулу (1). Подставляя значения ( small a ) и ( small S ) в (1), получим:
Ответ:
Высота треугольника по трем сторонам
Формула площади треугольника по трем сторонам имеет следующий вид (см. статью на странице Площадь треугольника онлайн):
где ( small a, b, c ) стороны треугольника а полупериод ( small p ) вычисляется из формулы:
Высота треугольника, отпущенная на сторону ( small a) вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления высоты треугольника по трем сторонам:
Пример 2. Известны стороны треугольника: ( small a=5, ) ( small b= 4, ) ( small c=7. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Найдем, сначала полупериод ( small p ) треугольника из формулы (3):
Подставляя значения ( small a , b, c ) и ( small p ) в (4), получим:
Ответ:
Высота треугольника по двум сторонам и радиусу описанной окружности
Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:
Далее, из теоремы синусов имеем:
Подставляя (6) в (7), получим:
Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:
(small max (b,c) ≤2R Пример 3. Известны стороны треугольника: ( small b=7, ) ( small c= 3 ) и радиус описанной окружности ( small R=4. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Проверим сначала условие (9):
(small max (7,3) ≤2 cdot 4 Ответ: ( small 2frac<5><8>. )
Высота треугольника по стороне и прилежащему к ней углу
Найдем высоту ( small h_a ) треугольника на рисунке 7. Из теоремы синусов имеем:
( small frac<large h_a><large sin angle B>=frac<large c><large sin 90°>, )
| ( small h_a=c cdot sin angle B. ) | (11) |
Пример 4. Известны сторона ( small c=12 ) треугольника и прилежащий угол ( small angle B=30°. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Для нахождения высоты треугольника подставим значения ( small c=12 ) и ( small angle B=30° ) в (11). Имеем:
[spoiler title=”источники:”]
http://matworld.ru/geometry/vysota-treugolnika.php
[/spoiler]
Автор вопроса: Марат Новиков
Опубликовано: 02/04/2023
Как найти высоту в шаре?
У нас есть 18 ответов на вопрос Как найти высоту в шаре? Скорее всего, этого будет достаточно, чтобы вы получили ответ на ваш вопрос.
- Как найти сегмент шара?
- Как найти объем шарового сектора?
- Как найти высоту в шаре? Ответы пользователей
- Как найти высоту в шаре? Видео-ответы
Отвечает Артём Дадашов
Как найти высоту сегмента в шаре? … Есть две основные формулы: h= R-√(R^2-r^2); h= Sсгм/(2pi*R). Здесь R – радиус сферы, r – радиус основания сегмента, Sсгм – …
Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара. Как можно получить шар?
Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
Как найти сегмент шара?
Вычисляется по формуле: V = πh²(3R − h)/3. (R — радиус шара, h — высота шарового сегмента, π — число Пи).
Как найти объем шарового сектора?
Формула для расчета объема шарового сектора : V = 2 / 3 * п * R2 * h. п – число п = 3,14. R – радиус шара. h – высота сектора.
Отвечает Анатолий Иванов
V(сегм.) = π H 2 · ( R − H 3 ) , где R — радиус шара, H — высота шарового сегмента.
Отвечает Андрей Вилков
Шар – радиус, объем, площадь, диаметр, окружность … Найти площадь поверхности шарового сегмента, зная радиус и высоту, можно, умножив длину окружности, …
Отвечает Роман Садыков
Через радиус основания сегмента и его высоту
Отвечает Рома Кредо
h – высота сегмента; перпендикуляр от центра основания сегмента до точки на сфере. Формула для нахождения объема сектора шара. Чтобы найти объем шарового …
Отвечает Александр Прямиков
Площадь поверхности шарового сегмента S = 2πRh, в которой R – радиус круга, а h – высота шарового сегмента. Для шарового сегмента также …
Отвечает Ильнар Логинов
дано два шара одинаковой массы один лежит а второй мы сбрасываем на первый (со скоростью Vo) с высоты h, как найти высоту на которую …
Отвечает Даниил Халиков
Основания шарового слоя – это сечения шара плоскостями. ∙ Высота …
7 класс, 17 урок, Медианы, биссектрисы и высоты треугольника
По вопросам размещения рекламы на наших видеороликах – https://api.whatsapp.com/send?phone=77072132054. Решаем …

Как найти высоту трапеции, зная все стороны?
Рассказываю о том, как искать высоту в трапеции, все стороны которой даны. Использую дополнительное построение …

Объем и площадь поверхности шара
Еще все выражение на четыре третьих вот предложили это число на множители чтобы легче найти радиус ну а теперь …

Построение высоты в треугольнике
Created by InShot:https://inshotapp.com/share/youtube.html.

19. Геометрия на ЕГЭ по математике. Высота в прямоугольном треугольнике и ее свойства
7 (495) 984 09 27, +7 (800) 775 06 82 (бесплатный звонок по России) Наш адрес: г. Москва, м. Пушкинская, Страстной …

Скачать материал
без ожидания

Скачать материал
без ожидания


- Сейчас обучается 27 человек из 17 регионов


- Сейчас обучается 20 человек из 16 регионов


- Сейчас обучается 120 человек из 40 регионов


Описание презентации по отдельным слайдам:
-

1 слайд
Сфера и шар.
Сш №12 п. Осакаровка -

2 слайд
Сферой называется поверхность, которая состоит из всех точек пространства, находящихся на заданном расстоянии от данной точки. Эта точка называется центром, а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой. Шар состоит из всех точек пространства, находящихся на расстоянии не более заданного от данной точки.
-

3 слайд
Отрезок, соединяющий центр шара с точкой на его поверхности, называется радиусом шара. Отрезок, соединяющий две точки на поверхности шара и проходящий через центр, называется диаметром шара, а концы этого отрезка – диаметрально противоположными точками шара.
-

4 слайд
Чему равно расстояние между диаметрально противоположными точками шара, если известна удаленность точки, лежащей на поверхности шара от центра?
?
18 -

5 слайд
Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси.
-

6 слайд
Пусть известна площадь полукруга. Найдите радиус шара, который получается вращением этого полукруга вокруг диаметра.
?
4 -

7 слайд
Теорема. Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра шара на секущую плоскость, попадает в центр этого круга.
Дано:Доказать:
-

8 слайд
Доказательство:
Рассмотрим прямоугольный треугольник, вершинами которого являются центр шара, основание перпендикуляра, опущенного из центра на плоскость, и произвольная точка сечения. -

9 слайд
Следствие. Если известны радиус шара и расстояние от центра шара до плоскости сечения, то радиус сечения вычисляется по теореме Пифагора.
-

10 слайд
Пусть известны диаметр шара и расстояние от центра шара до секущей плоскости. Найдите радиус круга, получившегося сечения.
?
10 -

11 слайд
Чем меньше расстояние от центра шара до плоскости, тем больше радиус сечения.
-

12 слайд
В шаре радиуса пять проведен диаметр и два сечения, перпендикулярных этому диаметру. Одно из сечений находится на расстоянии три от центра шара, а второе – на таком же расстоянии от ближайшего конца диаметра. Отметьте то сечение, радиус которого больше.
? -

13 слайд
Задача.
На сфере радиуса R взяты три точки, являющиеся вершинами правильного треугольника со стороной а. На каком расстоянии от центра сферы расположена плоскость, проходящая через эти три точки?
Дано:Найти:
-

14 слайд
Рассмотрим пирамиду с вершиной в центре шара и основанием – данным треугольником.
Решение: -

15 слайд
Найдем радиус описанной окружности, а затем рассмотрим один из треугольников, образованных радиусом, боковым ребром пирамиды и высотой,. Найдем высоту по теореме Пифагора.
Решение: -

16 слайд
Наибольший радиус сечения получается, когда плоскость проходит через центр шара. Круг, получаемый в этом случае, называется большим кругом. Большой круг делит шар на два полушара.
-

17 слайд
В шаре, радиус которого известен, проведены два больших круга. Какова длина их общего отрезка?
?
12 -

18 слайд
Плоскость и прямая, касательные к сфере.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью. Касательная плоскость перпендикулярна радиусу, проведенному в точку касания. -

19 слайд
Пусть шар, радиус которого известен, лежит на горизонтальной плоскости. В этой плоскости через точку касания и точку В проведен отрезок, длина которого известна. Чему равно расстояние от центра шара до противоположного конца отрезка?
?
6 -

20 слайд
Прямая называется касательной, если она имеет со сферой ровно одну общую точку. Такая прямая перпендикулярна радиусу, проведенному в точку касания. Через любую точку сферы можно провести бесчисленное множество касательных прямых.
-

21 слайд
Дан шар, радиус которого известен. Вне шара взята точка, и через нее проведена касательная к шару. Длина отрезка касательной от точки вне шара до точки касания также известна. На каком расстоянии от центра шара расположена внешняя точка?
?
4 -

22 слайд
Стороны треугольника 13см, 14см и 15см. Найти расстояние от плоскости треугольника до центра шара, касающегося сторон треугольника. Радиус шара равен 5 см.
Задача.
Дано:Найти:
-

23 слайд
Сечение сферы, проходящее через точки касания, – это вписанная в треугольник АВС окружность.
Решение: -

24 слайд
Вычислим радиус окружности, вписанной в треугольник.
Решение: -

25 слайд
Зная радиус сечения и радиус шара, найдем искомое расстояние.
Решение: -

26 слайд
Через точку на сфере, радиус которой задан, проведен большой круг и сечение, пересекающее плоскость большого круга под углом шестьдесят градусов. Найдите площадь сечения.
?
π -

27 слайд
Взаимное расположение двух шаров.
Если два шара или сферы имеют только одну общую точку, то говорят, что они касаются. Их общая касательная плоскость перпендикулярна линии центров (прямой, соединяющей центры обоих шаров). -

28 слайд
Касание шаров может быть внутренним и внешним.
-

29 слайд
Расстояние между центрами двух касающихся шаров равно пяти, а радиус одного из шаров равен трем. Найдите те значения, которые может принимать радиус второго шара.
?
2
8 -

30 слайд
Две сферы пересекаются по окружности. Линия центров перпендикулярна плоскости этой окружности и проходит через ее центр.
-

31 слайд
Две сферы одного радиуса, равного пяти, пересекаются, а их центры находятся на расстоянии восьми. Найдите радиус окружности, по которой сферы пересекаются. Для этого необходимо рассмотреть сечение, проходящее через центры сфер.
?
3 -

32 слайд
Вписанная и описанная сферы.
Сфера (шар) называется описанной около многогранника, если все вершины многогранника лежат на сфере. -

33 слайд
Какой четырехугольник может лежать в основании пирамиды, вписанной в сферу?
? -

34 слайд
Сфера называется вписанной в многогранник, в частности, в пирамиду, если она касается всех граней этого многогранника (пирамиды).
-

35 слайд
В основании треугольной пирамиды лежит равнобедренный треугольник, основание и боковые стороны известны. Все боковые ребра пирамиды равны 13. Найти радиусы описанного и вписанного шаров.
Задача.
Дано:Найти:
-

36 слайд
I этап.
Нахождение радиуса вписанного шара.
1) Центр описанного шара удален от всех вершин пирамиды на одинаковое расстояние, равное радиусу шара, и в частности, от вершин треугольника АВС. Поэтому он лежит на перпендикуляре к плоскости основания этого треугольника, который восстановлен из центра описанной окружности. В данном случае этот перпендикуляр совпадает с высотой пирамиды, поскольку ее боковые ребра равны.
Решение: -

37 слайд
2) Вычислим радиус описанной около основания окружности.
Решение: -

38 слайд
3) Найдем высоту пирамиды.
Решение: -

39 слайд
4) Радиус описанного шара найдем из треугольника, образованного радиусом шара и частью высоты, прилежащей к основанию пирамиды.
Решение: -

40 слайд
Соединим центр вписанного шара со всеми вершинами пирамиды, тем самым мы разделим ее на несколько меньших пирамид. В данном случае их четыре. Высоты всех пирамид одинаковы и равны радиусу вписанного шара, а основания – это грани исходной пирамиды.
Решение:
II этап.
Нахождение радиуса вписанного шара. -

41 слайд
1) Найдем площадь каждой грани пирамиды и ее полную поверхность.
Решение: -

42 слайд
2) Вычислим объем пирамиды
и радиус вписанного шара.
Решение: -

43 слайд
Второй способ вычисления радиуса вписанной сферы основан на том, что центр шара, вписанного в двугранный угол, равноудален от его сторон, и, следовательно, лежит на биссекторной плоскости.
-

44 слайд
Сторона основания правильной четырехугольной пирамиды равна 6, а угол между основанием и боковой гранью равен 600. Определить радиус вписанной сферы.
Задача.
Дано:Найти:
-

45 слайд
Проведем сечение через вершину пирамиды и середины двух противоположных сторон основания.
Отрезок, соединяющий центр сферы с серединой стороны основания, делит пополам двугранный угол при основании.
Решение: -

46 слайд
Рассмотрим треугольник, полученный в сечении, и найдем искомый радиус из тригонометрических соотношений.
Решение:
Краткое описание документа:
Сферой называется поверхность, которая состоит из всех точек
пространства, находящихся на заданном расстоянии от данной точки. Эта точка называется центром,
а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой.
Шарсостоит из всех точек пространства, находящихся на расстоянии не более заданного от данной точки.
Чему равно расстояние между диаметрально противоположными точками шара, если известна удаленность точки, лежащей на поверхности шара от центра?
Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси.
Пусть известна площадь полукруга. Найдите радиус шара, который получается вращением этого полукруга вокруг диаметра.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 251 905 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 14.01.2015
- 1171
- 2
- 14.01.2015
- 615
- 0
Рейтинг:
5 из 5
- 14.01.2015
- 6297
- 110
Рейтинг:
5 из 5
- 14.01.2015
- 1898
- 1
- 14.01.2015
- 974
- 0
Рейтинг:
1 из 5
- 14.01.2015
- 2398
- 7
- 14.01.2015
- 585
- 0
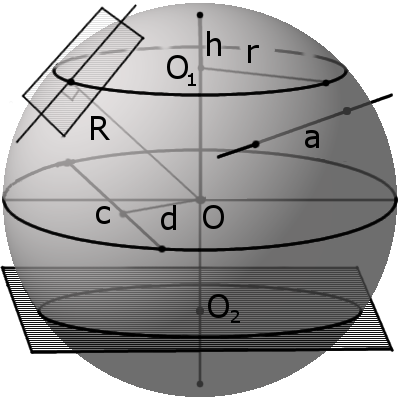
Сфера, шар, сегмент и сектор. Формулы и свойства сферы
Определение.
Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение. Радиус сферы (шара) (R) – это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) – это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула. Объём шара:
| V = | 4 | πR3 = | 1 | πD3 |
| 3 | 6 |
Формула. Площадь поверхности сферы через радиус или диаметр:
S = 4πR2 = πD2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:
x2 + y2 + z2 = R2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x0, y0, z0) в декартовой системе координат:
(x – x0)2 + (y – y0)2 + (z – z0)2 = R2
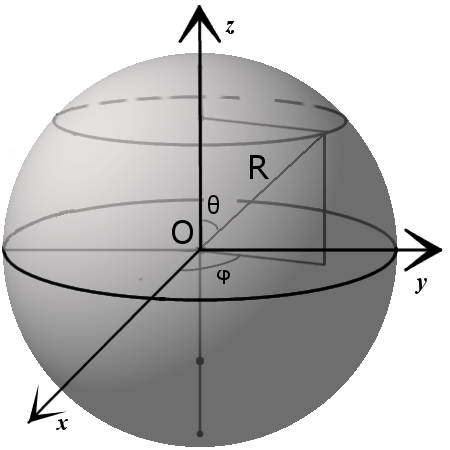
3. Параметрическое уравнение сферы с центром в точке (x0, y0, z0):
x = x0 + R · sin θ · cos φ
y = y0 + R · sin θ · sin φ
z = z0 + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].
Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы – это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Определение. Хорда сферы (шара) – это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость – это плоскость, которая пересекает сферу.
Определение. Диаметральная плоскость – это секущая плоскость, проходящая через центр сферы или шара, сечение образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d < R
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m < R
Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:
r = √R2 – m2,
где R – радиус сферы (шара), m – расстояние от центра шара до секущей плоскости.
Определение. Полусфера (полушар) – это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение.Касательная к сфере – это прямая, которая касается сферы только в одной точке.
Определение.Касательная плоскость к сфере – это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
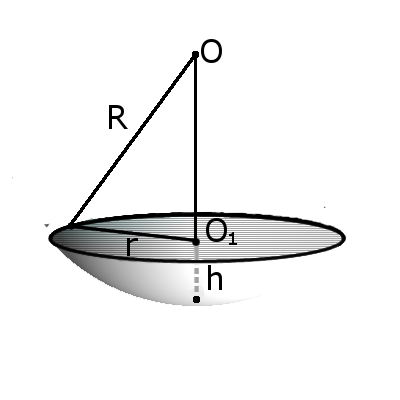
Определение. Сегмент шара – это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2πRh
Формула. Объём сегмента сферы с высотой h через радиус сферы R:

Определение. Срез шара – это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.
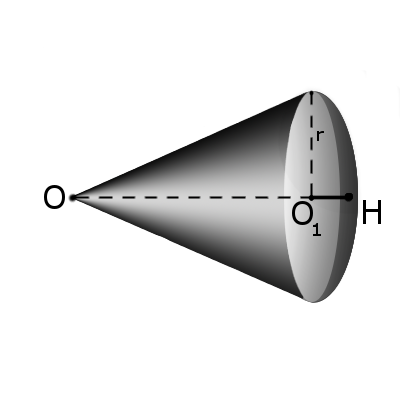
Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.
Формула. Площадь поверхности сектора S с высотой O1H (h) через радиус шара OH (R):
S = πR(2h + √2hR – h2)
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.
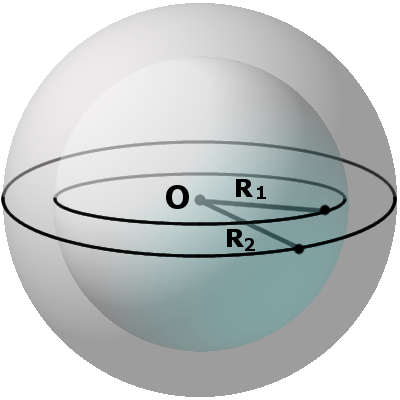
Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.
