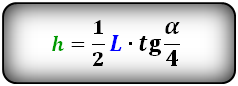В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить объем сегмента шара, а также разберем пример решения задачи для закрепления теоретического материала.
- Определение сегмента шара
-
Формулы для нахождения объема шарового сегмента
- Через радиус шара и высоту сегмента
-
Через радиус основания сегмента и его высоту
- Пример задачи
Определение сегмента шара
Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.
- R – радиус шара;
- r – радиус основания сегмента;
- h – высота сегмента; это длина перпендикуляра от центра его основания (точка O2) до точки на поверхности шара.
Формулы для нахождения объема шарового сегмента
Пояснения:
- В формулах ниже используется радиус шара (R) или радиус основания сегмента (r). Поэтому, если изначально дан их диаметр (d), то чтобы найти требуемый радиус, нужно соответствующий диаметр разделить на два.
- Число π округленно равняется до 3,14.
Через радиус шара и высоту сегмента
Чтобы найти объем (V) сегмента шара, необходимо знать радиус шара и высоту сегмента.
Через радиус основания сегмента и его высоту
Вычислить объем (V) шарового сегмента можно, зная его высоту и радиус основания (круга).
Данная формула получена следующим образом:
Радиус шара можно выразить через радиус основания сегмента и его высоту:
Таким образом, заменив R в первой формуле для расчета объема на выражение выше, получаем:
Пример задачи
Найдите объем сегмента шара, если известно, что его высота равняется 4 см, а радиус шара – 9 см.
Решение
В данном случае с учетом известных значений нам подходит первая формула:
Объёмы шарового сегмента, шарового слоя и шарового сектора. Площадь сферы
План урока
- Объём шарового сегмента;
- Объём шарового слоя;
- Объём шарового сектора;
- Площадь сферы.
Цели урока
- Знать формулы нахождения объёмов шарового сегмента, слоя и сектора, площади сферы;
- Уметь находить объёмы шаровых сегмента, слоя, сектора, площадь сферы.
Разминка
- Как найти объём шара?
- Во сколько раз уменьшится объём шара, если его диаметр уменьшить в 5 раз?
Рис. 1. Шаровой сегмент
Объём шарового сегмента
Для пирамиды и конуса помимо формул объёмов этих фигур, вы изучили формулы для нахождения объёмов усеченных пирамид и конуса. Для шара есть формулы объёмов его частей.
Мы рассмотрим шаровой сегмент, шаровой слой и шаровой сектор.
Начнем с шарового сегмента (рис. 1).
Шаровым сегментом
называется часть шара, отсекаемая от него какой-нибудь плоскостью.
Рис. 2. Шаровой сегмент
Круг, получающийся в сечении, называется
основанием
каждого из этих сегментов, а длины отрезков диаметра, перпендикулярного к секущей плоскости, называются
высотами сегмента
(на рис. 2 высоты сегментов обозначены h и h1).
Если радиус шара равен R, а высота сегмента равна h, то объём шарового сегмента вычисляется по формуле
Vсегмента=πh2R-13h.
Докажем эту формулу.
Пусть x – расстояние от центра шара до точки, принадлежащей высоте сегмента (рис. 2). При этом x может принимать значения от (R-h) до R.
Площадь сечения, проведенного на расстоянии x от центра шара перпендикулярно высоте сегмента, обозначим S(x). Так как сечение – это круг радиуса r1, причём r12=R2-x2, тогда площадь сечения можно вычислить по формуле S(x)=πr12=πR2-x2.
Используя основную формулу для вычисления объёма тел с помощью определенного интеграла, получаем:
V=∫R-hRS(x)dx=∫R-hRπR2-x2dx=πR2∫R-hRdx-π∫R-hRx2dx=
=πR2·xR-hR-π·x33R-hR=πh2R-13h.
Пример 1
Найдите объем шарового сегмента, если радиус шара равен 6 см, а высота сегмента, составляет треть диаметра шара.
Решение
Найдем высоту сегмента
h=13 D=13·2R=23·6=4 (см).
По формуле найдем объём сегмента
V=πh2R-13h=π·42·6-43=224π3 см3.
Ответ: 224π3 см3.
Упражнение 1
1. Найдите объем шарового сегмента, если радиус шара равен 12 см, а высота сегмента составляет четверть диаметра шара.
2. Найдите высоту шарового сегмента, если радиус шара равен 4, а объём шарового сегмента равен 27π.
Объём шарового слоя
Следующая часть шара, которую мы рассмотрим, – это шаровой слой (рис. 3). Его можно получить, если разрезать шар двумя параллельными плоскостями. Сделав это действие, получим два сегмента и один слой.
Дадим определение шарового слоя.
Шаровым слоем
называется часть шара, заключенная между двумя параллельными секущими плоскостями.
Рис. 3. Шаровой слой
Расстояние h между сечениями называется
высотой слоя
, а сами сечения –
основаниями слоя
.
Объем шарового слоя можно вычислить как разность объемов двух шаровых сегментов. Например, объем шарового слоя, изображенного на рисунке 3, равен разности объемов шаровых сегментов с высотами AC и BC:
Vслоя=VсегмAC-VсегмBC.
Пример 2
Диаметр шара разделен на три равные части и через точки деления проведены плоскости, перпендикулярные к диаметру (рис. 4). Найдите объем получившегося шарового слоя, если радиус шара равен R=3.
Рис. 4. Шаровой слой
Решение
Объём слоя найдем как разность объёмов сегмента с высотой AD и сегмента с высотой AC.
По условию AC=CD=13 D=2. Тогда h1=AD=4, h2=AC=2.
Найдем объём
Vслоя=Vсегм AD-VсегмAC=
=πh12R-13h1-πh22R-13h2=
=π·423-43-π·223-23=52π3.
Ответ: 52π3.
Упражнение 2
На диаметре шара AB отмечены точки C, D причём AC=14 D, AD=34 D, где D – диаметр шара. Через точки деления проведены плоскости, перпендикулярные к диаметру. Найдите объем получившегося шарового слоя, если радиус шара равен R=6.
Объём шарового сектора
Дадим определение шарового сектора (рис. 5).
Шаровым сектором
называется тело полученное вращением кругового сектора с углом, меньшим 90°, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.
Рис. 5. Шаровой сектор
Шаровой сектор состоит из сегмента и конуса (рис. 5).
Если радиус шара равен R, а высота сегмента равна h, то высота конуса равна (R-h), а площадь основания конуса равна:
Sосн=πr2=πR2-(R-h)2=πh(2R-h).
Вычислим объём шарового сектора.
Vсектора=Vсегмента+Vконуса,
Vсектора=πh2R-13h+13πh(2R-h)·(R-h)=23πR2h.
Если радиус шара равен R, а высота шарового сегмента равна h, то объём шарового сектора вычисляется по формуле
Vсектора=23πR2h.
Пример 3
Найдите объем шарового сектора, если радиус окружности основания соответствующего шарового сегмента равен 4, а радиус шара равен 5 (рис. 6).
Рис. 6. Шаровой сектор
Решение
Найдем высоту сегмента. В прямоугольном треугольнике ACO по теореме Пифагора найдем OC:
OC=R2-r2=52-42=3.
Тогда h=BC=BO-OC=5-3=2.
По формуле найдем объём сектора:
V=23πR2h=23π·52·2=100π3.
Ответ: 100π3.
Упражнение 3
1. Найдите объем шарового сектора, если радиус окружности основания соответствующего шарового сегмента равен 5 см, а радиус шара равен 13 см.
2. Найти объем шарового сегмента, если радиус окружности основания соответствующего шарового сегмента 8 см, а его высота – 4 см.
Площадь сферы
Некоторое время назад мы определили без доказательства, что площадь сферы радиуса R можно вычислить по формуле S=4πR2. Также мы выяснили, что объём тела можно рассчитать по формуле V=43πR3.
Эти формулы, конечно, связаны некоторым соотношением. Дело в том, что площадь сферы радиуса R – это производная объёма шара, ограниченного этой сферой, по радиусу.
Действительно,
V'(R)=43πR3’=43π·R3’=43π·3R2=4πR2.
Контрольные вопросы
1. Чем шаровой сегмент отличается от шарового сектора?
2. Как можно получить шаровой слой?
3. Как найти объём этих частей шара?
Ответы
Упражнение 1
1. 360π см3.
2. 3.
Упражнение 2
198π.
Упражнение 3
1. 338π3 см3.
2. 800π3 см3.
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.
Рисуется большой круг.
|
|
|
Круг с центром (A) — основание шарового сегмента. (AC = r) — радиус основания шарового сегмента,
(AB = H) — высота шарового сегмента,
(OC = R) — радиус шара.
Площадь сферического сегмента вычисляется по формуле
Объём шарового сегмента вычисляется по формуле
(V(сегм.) =)
πH2
·(R
−H3)
, где (R) — радиус шара, (H) — высота шарового сегмента.
В формулах для сегмента не используется радиус основания сегмента, а используется радиус шара.
Источники:
Рисунки © Якласс
Формула высоты сегмента круга
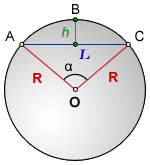
Сегмент – часть круга ABC, отсеченная хордой AC
h – высота сегмента ABC
L – хорда AC
R – радиус кружности
O – центр окружности
α – центральный угол AOC
Формула высоты через радиус и центральный угол, (h):
Формула высоты через хорду и центральный угол, (h):
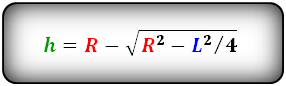
Формула высоты через радиус и хорду, (h):
Дополнительные формулы для окружности:
- Подробности
-
Автор: Administrator
-
Опубликовано: 16 октября 2011
-
Обновлено: 13 августа 2021
Поскольку шаровой сегмент представляет собой часть сферы, сечение которой находится под прямым углом к оси вращения, следовательно, становится возможным найти объем шарового сегмента, площадь поверхности, периметр сечения сферы и его диаметр, зная радиус и высоту шарового сегмента.
Диаметр шарового сегмента, также как и диаметр сферы, равен удвоенному радиусу тела.
d=2r
Периметр сечения сферы, образующего шаровой сегмент, является длиной окружности с заданным радиусом, и равен удвоенному произведению радиуса на число π.
P=2πr
Чтобы вычислить объем шарового сегмента через радиус и высоту, нужно найти треть произведения числа π и квадрата радиуса на разность утроенного радиуса и высоты.
V=(πh^2 (3R-h))/3
Найти площадь поверхности шарового сегмента, зная радиус и высоту, можно, умножив длину окружности, являющуюся периметром сечения сферы, на высоту шарового сегмента. Так как периметр сечения равен удвоенному произведению числа π и радиуса шарового сегмента, то формула площади поверхности шарового сегмента выглядит следующим образом:
S=2πrh