Как найти высоту шарового слоя - Сайт, где вы сможете решить свои вопросы

({color{red}{{small{textbf{Факт 1. Про шаровой сегмент}}}}})
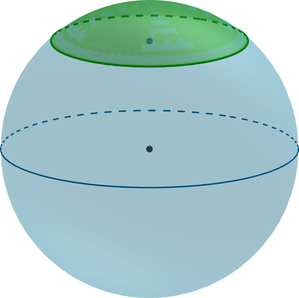
(bullet) Шаровой сегмент – шасть шара, отсекаемая от него плоскостью ((alpha)).

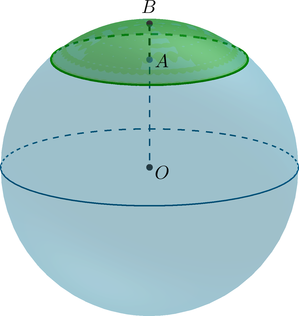
(bullet) Если (O) – центр шара, (OB=R) – радиус шара, перпендикулярный плоскости (alpha), (A) – центр круга (основания шарового сегмента), а также точка пересечения радиуса (OB) c этим кругом, то
(H=AB) – высота шарового сегмента.
(bullet) Площадь сферического сегмента (часть сферы, отсекаемая от нее плоскостью (alpha)) вычисляется по формуле [S=2pi cdot RH] (bullet) Объем шарового сегмента вычисляется по формуле [V=pi H^2cdot left(R-frac13Hright)]

({color{red}{{small{textbf{Факт 2. Про шаровой слой}}}}})
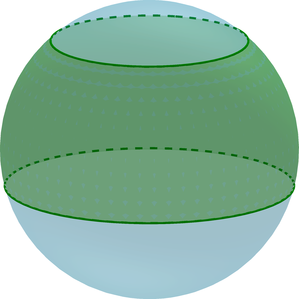
(bullet) Шаровой слой – часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.

(bullet) Основания шарового слоя – это сечения шара плоскостями.
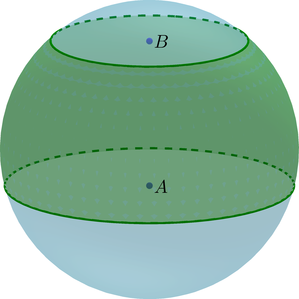
(bullet) Высота (H=AB) шарового слоя – это расстояние между основаниями.
(bullet) Площадь сферической части шарового слоя равна [S=2pi RH] где (R) – радиус шара.
(bullet) Объем шарового слоя равен разности объемов двух шаровых сегментов: [V=V_{A}-V_{B}]

({color{red}{{small{textbf{Факт 3. Про шаровой сектор}}}}})
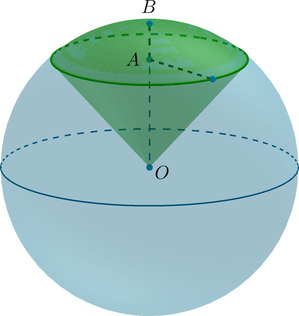
(bullet) Шаровой сектор – часть шара, ограниченная сферической частью шарового сегмента и боковой поверхностью конуса, имеющего то же основание, что и шаровой сегмент.

(bullet) Если (H=AB), то объем шарового сектора равен [V=dfrac23pi R^2cdot H]

Источник

Помогите найти высоту слоя шара

Тимур Ильясов

Ученик

(95),
на голосовании

10 месяцев назад

В шаровом слое радиусы оснований 7 см, 12 см, радиус шара 15 см. Найти высоту шара

Голосование за лучший ответ

Владимир Костюк

Искусственный Интеллект

(120344)

11 месяцев назад

Решай всё по Пифагору, 2 раза. 15см – это гипотенуза. 12 и 7 – катеты. Оба они меньше 15, а это значит, что лежат (находятся по одну ) сторону “полушария”. Разность найденных катетов = высота слоя. Картинка “чужая”, смени девятку на семерку.

Похожие вопросы

Источник

Шаровой слой

Шар пересеченный двумя параллельными плоскостями

Шаровой слой — часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар^[1].

Содержание

1 Связанные определения
2 Свойства
3 Вариации и обобщения
4 См. также
5 Примечания

Связанные определения[править | править код]

Основания шарового слоя — это сечения шара, образовавшиеся в результате пересечения шара двумя параллельными плоскостями.
Высота шарового слоя — это расстояние между основаниями слоя.

Свойства[править | править код]

Объём шарового слоя можно найти как разность объёма двух шаровых сегментов:
$V=pi left[H_{1}^{2}left(R-{frac {1}{3}}H_{1}right)-H_{2}^{2}left(R-{frac {1}{3}}H_{2}right)right],$
где — объём шарового слоя, — высота большего шарового сегмента, — высота меньшего шарового сегмента, — радиус шара.
Площадь сферической части поверхности шарового слоя (так называемый сферический пояс) зависит только от высоты слоя и радиуса шара^[2]:

где

— площадь сферического пояса,

— высота шарового слоя,

— радиус шара.

Вариации и обобщения[править | править код]

В физике под шаровым слоем часто понимают слой, ограниченный сферами радиуса и , для маленького . Объем шарового слоя в этом случае с точностью до O ${displaystyle (dr^{2})}$ равен $dV=4pi r^{2}dr$ .

См. также[править | править код]

Сферический слой

Примечания[править | править код]

↑ Мантуров О. В. и др. Словарь математических терминов. — М.: Просвещение, 1965. — С. 512.
↑ Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров. — М.: Советская энциклопедия, 1988. — С. 638.

Источник

На этом уроке мы введём понятия шарового сегмента,
шарового слоя и шарового сектора. А также выведем формулы для вычисления их объёмов.

Прежде чем приступить к рассмотрению данной темы,
давайте вспомним, что такое шар.

Определение:

Итак, шар
– это совокупность всех точек пространства, находящихся от данной точки на
расстоянии, не больше данного. Причём, данная точка называется центром
шара, а данное расстояние – радиусом шара.

Самой простой фигурой, которую можно начертить,
используя шар, является шаровой сегмент.

Определение:

Шаровым сегментом
называется часть шара, отсекаемая от него какой-нибудь плоскостью.

На экране вы видите, как секущая плоскость ,
проходящая через точку ,
разделяет шар на два шаровых сегмента. Круг, получившийся в сечении, называется
основанием каждого из этих сегментов, а длины отрезков и
диаметра
,
перпендикулярного к секущей плоскости, называются высотами
сегментов.

Верно следующее утверждение: если радиус шара равен ,
а высота сегмента равна ,
то объем шарового
сегмента можно вычислить по формуле:

Докажем это утверждение. Доказывать
будем с помощью определённого интеграла.

Проведём ось перпендикулярно
к плоскости .
Тогда площадь ,

при .

Вычислим объём шарового сегмента с помощью основной
формулы объёма тела. Вспомним её: .

Итак, применим основную формулу для вычисления объёмов
тел получаем, что объём шарового сегмента равен .

Что и требовалось доказать.

Заметим, что если высоту в
формуле объема шарового сегмента заменить
на ,
то получим формулу для нахождения объёма шара:

А если заменить высоту на
радиус ,
то получим формулу для нахождения объёма полушара.

Кстати, в жизни нас также окружают некоторые объекты,
имеющие форму очень близкую к форме шарового сегмента.

В современной авиации наиболее популярны парашюты в
виде сегмента.

Форму шарового сегмента нередко используют и в
архитектуре, интерьере, декоре.

Перейдём к шаровому слою.

Определение:

Шаровым слоем
называется часть шара, заключённая между двумя параллельными секущими плоскостями.

На экране вы видите изображение шарового слоя.

Круги, получившиеся в сечении шара плоскостями,
называются основаниями шарового слоя, а расстояние между
плоскостями – высотой шарового слоя.

Нетрудно заметить, что объём шарового слоя можно
вычислить, как разность объёмов двух шаровых сегментов.

Объём шарового слоя, изображённого на экране, равен
разности объёмов шаровых сегментов, высоты которых равны и
.

Если высота шарового слоя равна ,
а радиусы и
–
радиусы оснований шарового слоя соответственно, то объем шарового слоя можно
вычислить по формуле:

Декоративная свеча может служить примером шарового
слоя в жизни.

И теперь перейдём к шаровому сектору.

Определение:

Шаровым сектором
называется тело, которое получается при вращении кругового сектора с углом,
меньшим 90^о, вокруг прямой, содержащей один из ограничивающих круговой
сектор радиусов.

Обратите внимание, шаровой сектор состоит из шарового
сегмента и конуса. Причём шаровой сегмент имеет высоту ,
а конус высоту ,
где –
радиус шара.

Понятно, что шаровая поверхность пересекается с
конусом по окружности. Радиус этой окружности равен .

Если радиус шара равен ,
а высота шарового сегмента равна ,
то объем шарового
сектора можно найти по формуле:

Для того чтобы получить данную формулу необходимо
сложить объём конуса (с вершиной O), лежащего под плоскостью, и объём шарового сегмента,
лежащего над плоскостью.

Большой воздушный шар имеет форму близкую к форме
шарового сектора в жизни.

Перейдём к задачам.

Задача: радиус
шара равен см.
Вычислите объем шарового сегмента, если его высота равна см.

Решение: запишем
формулу для вычисления объёма шарового сегмента.

И подставим в неё радиус шара и высоту шарового
сегмента.

Запишем ответ.

Задача: по
разные стороны от центра шара проведены два параллельных сечения с площадью и
см².
Расстояние между сечениями равно см.
Определите объём получившегося шарового слоя.

Решение: запишем
формулу для вычисления объема шарового слоя.

Чтобы найти объём шарового слоя нам необходимо знать
его высоту и радиусы двух его оснований.

По условию задачи нам дано расстояние между сечениями,
как раз-таки это расстояние и есть высота данного шарового слоя, и она равна .

Теперь найдём чему равны радиусы оснований шарового
слоя. Напомню, что сечением шара плоскостью является круг. Площадь круга
вычисляется по формуле .
Отсюда найдём радиусы оснований шарового слоя. Тогда имеем, радиус одного основания
равен (см),
радиус второго основания равен (см).

Подставим радиусы оснований и высоту шарового слоя в
формулу его объёма. Посчитаем. Получаем, что объём данного шарового слоя равен .

Не забудем записать ответ

Задача: радиус
шара равен см.
Найдите объем шарового сектора, если высота шарового сегмента равна см.

Решение: запишем
формулу для вычисления объёма шарового сектора.

Подставим в неё радиус шара и высоту шарового
сегмента. Посчитаем. Получим, что объём данного шарового сектора равен .

Запишем ответ.

Итоги:

На этом уроке мы ввели понятия шарового сегмента,
шарового слоя и шарового сектора. Узнали, что шаровым сегментом называется
часть шара, отсекаемая от него какой-нибудь плоскостью. Шаровым слоем
называется часть шара, заключённая между двумя параллельными секущими плоскостями.
Шаровым сектором называется тело, которое получается при вращении кругового
сектора с углом, меньшим 90^о, вокруг прямой, содержащей один из ограничивающих
круговой сектор радиусов. А также вывели формулы для вычисления объёмов этих
тел.

Источник

Геометрия, 11 класс

Урок №14. Объем шара и его частей

Перечень вопросов, рассматриваемых в теме

Доказательство теорем об объемах шара и его частей и площади сферы
Определение частей шара
Решение задач на нахождение объемов шара, его частей и площади сферы

Основная литература:

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 10-11 учебник для общеобразов. учрежд.: база и профильн. М: Просвещение.2009

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни и др. – М.: Просвещение, 2014. – 255, сс. 121-126.

Дополнительная литература:

Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.

Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не больше данного R.

Радиусом шара называют всякий отрезок, соединяющий центр шара с точкой шаровой поверхности.

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара.

Концы любого диаметра шара называются диаметрально противоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара.

Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями

Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями

Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость.

Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.

Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы

Объем шара равен .

Объем шарового сегмента равен .

Объем шарового сектора равен .

Объем шарового слоя равен .

Площадь сферы равна S=4 πR².

Примеры и разбор решения заданий тренировочного модуля

№1. Круговой сектор радиуса R с центральным углом 60 градусов вращается вокруг одного из радиусов, образующих этот угол. Найдите объем тела вращения.

Решение:

При вращении кругового сектора АОВ вокруг радиуса ОА получается тело вращения – шаровой сектор радиуса R=ОА и высотой сектора h=DA. Объем его вычисляется по формуле: V= (2/3)*πR²*h. Рассмотрим сечение этого сектора (смотри рисунок): в прямоугольном треугольнике ОВD (радиус круга ОА перпендикулярен хорде ВС) угол ВОD равен 60° (дано). Значит Тогда высота шарового сектора равна h=DA=OA-OD=R-R/2=R/2.
V=(2/3)*π*R²*R/2=(1/3)πR³.

№2. Найдите объем шарового сектора, если радиус шара равен 6 см, а высота конуса, образующего сектор, составляет треть диаметра шара.

Решение:

Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной — центр шара. Формула объема шарового сектора: V = (2/3)*πR²*h, где h – высота сегмента. В нашем случае R=H+h, где Н – высота конуса, а h- высота сегмента. Тогда h = R-H = 6-4 =2, так как Н = (1/3)*2*R (дано). Значит V = (2/3)*π*36*2 = 48π.
Ответ: объем шарового сектора равен 48π

№3.По разные стороны от центра шара проведены два параллельных сечения с площадью и см². Расстояние между сечениями равно см. Определите объём получившегося шарового слоя.

Решение: запишем формулу для вычисления объема шарового слоя.

Чтобы найти объём шарового слоя нам необходимо знать его высоту и радиусы двух его оснований.

По условию задачи нам дано расстояние между сечениями, как раз-таки это расстояние и есть высота данного шарового слоя, и она равна .

Теперь найдём чему равны радиусы оснований шарового слоя. Напомню, что сечением шара плоскостью является круг. Площадь круга вычисляется по формуле . Отсюда найдём радиусы оснований шарового слоя. Тогда имеем, радиус одного основания равен (см), радиус второго основания равен (см).