Муниципальное
бюджетное общеобразовательное учреждение
«Средняя
общеобразовательная школа № 1» города Воткинска УР
Школьная
научно-практическая конференция учащихся
«Сохраним
мир потомкам»
«
Как определить высоту предмета с помощью подручных средств »
Авторы: Порсев Иван,
Захаров Влад
ученики 8 «а» класса МБОУ СОШ №1
Научный руководитель:
Колесникова Татьяна Павловна
учитель математики МБОУ СОШ №1
Воткинск, 2015г.
Содержание.
1 Введение…………………………………………………….1-3
2 Теоретическая часть………………………………………..3-4
3. Практическая часть………………………………………..4-18
4. Заключение…………………………………………………17-18
5. Использованная литература………………………………18-19
1 Введение
«Время
от времени следует производить
самые дикие эксперименты. Из них почти
никогда ничего не выходит, но если они
удаются, то результат бывает потрясающим»
Эразм Дарвин
В начале прошлого столетия великий
французский архитектор Корбюзье как-то воскликнул: «Все вокруг геометрия!».
Сегодня уже в начале 21-го столетия мы можем повторить это восклицание с еще
большим изумлением. В самом деле, посмотрите вокруг — всюду геометрия!
Современные здания и космические станции, авиалайнеры и подводные лодки,
интерьеры квартир и бытовая техника, микросхемы и даже рекламные ролики.
Воистину, современная цивилизация — это Цивилизация Геометрии. Геометрические
знания и умения, геометрическая культура и развитие являются сегодня
профессионально значимыми для многих современных специальностей, для дизайнеров
и конструкторов, для рабочих и ученых. Важно, что геометрия есть феномен
общечеловеческой культуры. Некоторые теоремы геометрии являются одними из
древнейших памятников мировой культуры. Геометрические знания широко
применяются в жизни — в быту, на производстве, в науке.
Геометрия – это целый мир, который
окружает нас с самого рождения. Ведь все, что мы видим вокруг, так или иначе
относится к геометрии, ничто не ускользает от ее внимательного взгляда.
Геометрия помогает человеку идти по миру с широко открытыми глазами, учит
внимательно смотреть вокруг и видеть красоту обычных вещей, смотреть и думать,
думать и делать выводы. Использование различных приборов, механизмов и
приспособлений в наше время значительно упрощает жизнь современных людей. Но
иногда возникают ситуации, когда нет возможности применить технические
средства. Например: довольно часто туристам требуется определить расстояния на
местности, оценить размеры предметов. Из-за отсутствия приборов это можно сделать
с помощью подручных средств или на глаз.
Актуальность исследования
1. Данная тема
является дополнением и углублением изученных в курсе математики и физики
методов измерения высоты здания.
2. Приобретенный
опыт позволит находить без каких-либо сложных технических устройств расстояние
до недоступных точек наиболее
удобным способом.
3. Изучение
данной темы помогает более глубоко подготовиться к вступительным экзаменам ЕГЭ
и ГИА.
Основная
цель нашей работы: научиться измерять недоступные высоты разными
способами, формирование математических приемов решения различных задач реальной
жизни
В связи, с чем были
поставлены следующие задачи:
1. знакомство с историческим и
теоретическим материалом по вопросу измерения высоты недосягаемого объекта;
2. решение практических задач;
3. Показать практическое применение
геометрических знаний в окружающем нас мире.
4. Показать умение проводить измерительные
работы на местности.
Гипотезы: 1.Длина шага человека равна половине его
роста.
2. Если человек знает подобие
треугольников, возникнет необходимость их применения в жизни
Методы исследования: Сравнительный, аналитический, теоретические
и экспериментальные исследования:
1. работа с литературой;
2. поиск информации во всемирной сети Интернет;
3. практические методы: измерения и сравнение;
4. математические расчеты
Объектом исследования нашей
работы является здание школы.
Предметом исследования – высота школы и способы её
измерения.
При написании данной
работы нами были использованы знания тем: “Пропорция”, “Равнобедренный
треугольник”, “Прямоугольный треугольник”, «Подобные треугольники», «Решение
треугольников» для измерений на местности, связать теорию с практикой и с
окружающим нас миром.
Для проведения экспериментов было
использовано следующее оборудование: линейка (цена деления – 1 мм), рулетка
(цена деления – 1 см), зеркало, транспортир (цена деления 1°), две рейки (их
длины будут указаны ниже), камушек, сферический груз, секундомер (цена деления
0,01 с), кусок мела, катушка светлых ниток, карандаш, маркер, ножницы,
воздушный шарик и др.
2.
Теоретическая часть.
«Природа говорит языком математики. Буквы
этого языка – круги, треугольники и иные математические фигуры.»
Галилео Галилей.
Высота пирамиды по способу Фалеса
Самый легкий и самый
древний способ – без сомнения, тот, которым греческий мудрец Фалес за шесть
веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался его
тенью. Фалес, говорит предание, избрал день и час, когда длина собственной его
тени равнялась его росту. В этот момент высота пирамиды должна равняться длине
отбрасываемой ее тени. Это, пожалуй, единственный случай, когда человек
извлекает пользу из своей тени.
Чтобы воспользоваться
тенью для решения задачи о высоте пирамиды, надо было знать некоторые
геометрические свойства треугольника, – именно следующие два:
1.
Углы при основании равнобедренного
треугольника равны, и обратно – что стороны, лежащие против равных углов
треугольника, равны между собою (открыл сам Фалес).
2.
Сумма углов всякого треугольника равна
двум прямым углам.
Вооруженный
этими знаниями Фалес вправе был заключить, что, его собственная тень равна его
росту, солнечные лучи встречают ровную почву под углом в половину прямого,
следовательно, вершина пирамиды, середина ее основания и конец ее тени должны
обозначить равнобедренный треугольник.
Этим простым способом очень удобно воспользоваться. Но в наших широтах не так
легко, как в Египте, подстеречь нужный для этого момент. Солнце у нас низко
стоит над горизонтом, и тени бывают, равны высоте отбрасывающих предметов лишь
в околополуденные часы летних месяцев.
Можно возразить, неужели без геометрии неясно, что во сколько раз дерево выше,
во столько раз и тень его длиннее?
Конечно, нет. Здесь нужно применить признак подобия треугольников по двум
углам.
Изменим
способ Фалеса: в солнечный день можно пользоваться любой тенью, какой бы длины
не была. Измерив свою тень или тень какого – либо шеста, вычисляем: АВ : ав
= ВС : вс, т.е. высота дерева во столько же раз больше собственной высоты, во
сколько раз тень дерева длиннее вашей тени.
Измерения голыми руками.
Рассматривается, что у большинства людей расстояние между концами
расставленных рук равно росту – правило, подмеченное гениальным художником и
ученым Леонардо да Винчи: оно позволяет пользоваться нашими «живыми метрами».
Исследовав учащихся нашего класса, мы убедились в этом.
Искусство мерить шагами.
Проходя 10м, и посчитав количество шагов, мы сделаем вывод, что на
самом деле длина шага человека равна половине его роста, считая до уровня глаз.
3.
Практическая часть.
Ход эксперимента.
|
Способ измерения |
Описание работы |
|||||||||||||||
|
1. |
При помощи журнала или записной книжки.
|
В качестве прибора для приблизительной оценки недоступной
|
||||||||||||||
|
2. |
Использование (или |
Оборудование: Чтобы Ход 1. 2. 3. от человека до зеркала, от школы до зеркала; рост 4. H/h=L/l, где H h L l 5. H 6. Вывод: |
||||||||||||||
|
3. |
Использование (в |
Оборудование: Необходимо Ход 1. 2. 3. 4. Вывод: |
||||||||||||||
|
4. |
Метод (ручку |
Оборудование: Этот Ход 1. 2. 3. 4. 5. 6. Вывод: |
||||||||||||||
|
5. |
Используя |
Оборудование: Для Ход 1. 2. 3. 4. H где H h l L Вывод: |
||||||||||||||
|
6. |
Используя |
Оборудование: Необходимое Ход 1. 2. H где h –рост человека l L Вывод: |
||||||||||||||
|
7. |
Используя |
Оборудование: Самый Ход 1. 2. 3. 3.
Вывод: |
||||||||||||||
|
8. |
Используя |
Оборудование: Самый Ход 1. 2. Вывод: |
||||||||||||||
|
7. |
Метод |
Прикрепим Выведем Замерим Теперь Исходя Очевидно, Наконец, Подставим Ответ |
||||||||||||||
|
10. |
Пиратский |
Возьмём Встав Ответ |
||||||||||||||
|
11. |
При |
Установим Направим Очевидно, Очевидно, Измерим Измерим Подставим Ответ: |
||||||||||||||
|
12. |
При помощи шеста, равного росту измеряющего. |
В этой задаче я использую шест, который |
Заключение.
«Правду
дополняет ясность»
–
Нильсон Бор.
В ходе нашего исследования мы применили
двенадцать методов измерения высоты объекта. Самый ненадежный – статистический
метод. Самым доступным способом является метод скаутов, т.к. он
требует минимум оборудования и всего одно измерение. Все остальные способы
связаны с применением метода сравнения, используя основы геометрии и законы
оптики.
Результаты всех измерений отражены в
таблице:
|
№ п/п |
Метод измерения |
Высота предметаH |
|
1. |
При помощи журнала или записной книжки. |
9,9 |
|
2. |
Использование зеркала |
10,1 |
|
3. |
Использование треугольника с углом 45 |
10 |
|
4. |
Метод скаутов |
10 |
|
5. |
Используя фотографию |
9,98 |
|
6. |
Используя тень предмета |
10,1 |
|
7. |
Используя статистический метод |
9,9 |
|
8. |
Используя воздушный шарик |
10 |
|
9. |
При помощи рейки известной длины |
9,9 |
|
10. |
При помощи шеста, равного росту |
10 |
|
Среднее арифметическое |
9,99 |
Видно, что разница между наименьшим и наибольшим значением высоты объекта
составляет всего 0,1 метра. Даже с учетом того, что достаточным опытом мы не
обладаем и проводили подобную работу впервые, можно утверждать – точность
наших измерений высокая.
Мы поинтересовались у заместителя
директора школы по АХЧ Мельниковой Натальи Александровны об истинной высоте
здания. По документации высота этой части школьного здания 10,12м. Так что наши
измерения достаточно верны.
Конечно, измерение высоты удаленного
предмета удобнее делать, когда в наличии имеется специальное измерительное
оборудование. Но не каждый раз удается предугадать ситуацию, которая может
возникнуть на прогулке или в туристическом походе. Вот тогда такие простые
знания пригодятся и даже помогут выйти из затруднительного положения.
Приведенные в приложении способы, подобраны так, чтобы можно было измерить
высоту здания, не имея при себе никакого сверх технологического оборудования.
Данная работа может служить хорошим пособием для подготовки к выпускным
экзаменам.
Список
литературы
1. Журнал
«Потенциал»
2. Физический
справочник
3. Учебник
физики А.А.Пинского
4. В.Н.Руденко.
Геометрия Просвещение 2009г.
5. Л.С.Атанасян.
Геметрия. Просвещение 2013г.
6. Научно-
практический и методический журнал. Математика в школе. № 2 Издательство
«Школьная пресса»
7. Газета.
Математика. Издательский дом «Первое сентября»
8. Я.И.Перельман.
Занимательная геометрия.
9. А.П.Савин
и др. Я познаю мир. Москва АСТ.2000
10. Б.В.Гнеденко
и др. Энциклопедический словарь юного математика. М. «Педагогика»1985г.
11. Г.И.Глейзер.
История математики в школе.Просвещение.1985.
12. http://taina.aib.ru/biography/nils-bor.htm
13. Газета
“Математика”№25 – 2000г., Автор Г.Душкина.
14. http://www.bajena.com/ru/?p=1004
15. http://visotki.ru/m2.php
16. http://www.mmforce.net/msu/heart
17. http://www.fizika.ru/
Тезисы выступления
Здравствуйте! Мы, учащиеся 11 класса Подовинновской школы, Листунов Лев и Тофан Татьяна представляем проект «Измерение высоты здания максимальным количеством необычных способов».Руководитель проекта Глазырина С.Н.
Однажды в интернете прочитал интересный случай о том, как один студент сдавал экзамен по физике.Преподаватель задал вопрос: “Объясните, каким образом можно измерить высоту здания с помощью барометра”.
Ответ студента был таким: “Нужно подняться с барометром на крышу здания, спустить барометр вниз на длинной веревке, а затем втянуть его обратно и измерить длину веревки, которая и покажет точную высоту здания”. После чего этот студент был выгнан из аудитории, но после подал на апелляцию, основываясь на том, что ответ был абсолютно правильным. На пересдаче студент заявил, что у него есть несколько решений проблемы, и он просто выбирал лучшее. И представил 25 решений этой задачи.
При этом признался, что и тогда знал ответ, но сыт по горло школой и колледжем, где учителя навязывают ученикам свой способ мышления. Студентом этим был Нильс Бор, впоследствии – великий датский физик, лауреат Нобелевской премии 1922г.
Тогда и пришла идея самим попытаться найти как можно больше способов измерения высоты предмета, например стены школьного здания.
Объектом исследования нашей работы является здание школы. Предметом исследования – высота школы и способы её измерения. Цель:1) Рассмотреть применение геометрии на практике. 2) Определить высоту здания школы.
Задачи: 1. Рассмотреть различные способы измерения высоты предметов. 2. Применить эти способы для измерения высоты здания школы. 3. Найти наиболее простой способ измерения высоты (с ошибкой не более 10%);
4. Сопоставить точность разных методов.
Гипотеза: Существует множество различных способов измерения высоты здания при помощи весьма незамысловатых приборов и даже без всяких приспособлений.
Способ 1. По инструкции
В интернете мы нашли инструкцию о том, как определить высоту стандартных многоэтажных зданий. Вот как она выглядит.
Посчитайте количество этажей в здании. Умножьте полученное число на 2,9 м и прибавьте к произведению 1,5 и 2 м. Но мы решили измерить высоту здания без крыши. Поэтому получаем: 2*2,9 +1,5 =7,5 м
Но здание нашей школы не является стандартным, поэтому этот способ измерение высоты нам не подходит.
Способ 2. При помощи рулетки
Сосчитаем количество ступенек лестницы с 1-го на 2-й этаж (их по 12) и измерим с помощью рулетки высоту одной ступеньки. Затем измерим высоту второго этажа. Очевидно, что высота школы равна:
Но это была высота здания изнутри!
Для проведения дальнейших экспериментов мы решили выбрать « мерку», и этой «меркой» стала я – Тофан Татьяна.
Поэтому мы измерили мой рост, расстояние до уровня глаз и длину шага.
В дальнейших исследованиях мы будем использовать именно эти измерения.
Способ 3. При помощи булавочного прибора.
Мы воспользуемся свойством равнобедренного прямоугольного треугольника, обратившись к услугам весьма простого прибора, который легко изготовить из дощечки или картонки и трех булавок. Я отошла на расстояние, чтобы продолжение гипотенузы треугольника проходило через верхний край стены здания. Расстояние получилось равно 628см. Высота школы равна 628 см плюс 150 см (уровень глаз над землей), равно 778 см = 7,78 м.
Способ 4.При помощи книги.
В качестве прибора для приблизительной оценки недоступной высоты мы использовали обычный учебник и ручку, всунутую в книжный переплёт. Она поможет вам построить в пространстве те два подобных треугольника, из которых получается искомая высота.
Расстояние от меня до школы Высота школы без уровня глаз над землёй
=
Ширина книги Высота ручки
Высота без уровня глаза над землей =
Высота стены школы =623+150=773см=7,73 м
Способ 5.
При помощи хитроумного прибора, не приближаясь к зданию.
В некоторых случаях неудобно подойти вплотную к основанию измеряемого здания. Для этого придуман хитроумный прибор, который, легко изготовить самому. Две планки скрепили под прямым углом так, чтобы планка от глаз до перпендикуляра равнялось планке от перпендикуляра до вершины. Вот и весь прибор. Чтобы измерить им высоту, держа его в руках, направили планку вертикально, и становились последовательно в двух местах: сначала в точку, где располагали прибор концом вверх, а затем в точке, подальше, где прибор держали вверх другим концом. Искомая высота стены здания равна сумме расстояния между метками и росту « мерки» до уровня глаз.
Расстояние между метками равно 6,2 м.Высота стены школы равна
6,2+1,5 = 7,7 м
Способ 6.
При помощи шеста 2 метра.
Воткнули шест в землю отвесно на некотором расстоянии от здания школы
и отошли от шеста назад, до того места, с которого, глядя на верхнюю точку стены здания видно на одной линии с ней верхнюю точку шеста.
Не меняя положения головы, смотрю по направлению горизонтальной прямой, замечая точки, в которых луч зрения встречает шест и здание, и прошу помощника сделать в этих местах пометки.
Из подобия треугольников получаем, что высота школы равна 6,37 м плюс 1,5м (уровень глаз над землей), равно = 7,87 м.
Способ 7.
При помощи шеста с вращающейся планкой.
Для этого поставим на некотором расстоянии от здания шест с вращающейся планкой и направим планку на верхнюю точку стены здания, как показано на рисунке. Из подобия треугольников следует: Высота школы равна2*6,3:1,6 = 7,88 м
Способ 8.
При помощи монеты.
Работая над проектом, я познакомилась вот с такой задачей:
Дерево высотой 15 м закрывается монетой диаметром 2 см, если ее держать на расстоянии 70 см от глаз. Найдите расстояние от дерева до наблюдателя. Меня эта задача очень заинтересовала. Мы решили попробовать измерить с помощью монеты высоту здания школы.
АВ = 750 см=7,5 м
Способ 9.
При помощи высотомера.
Из транспортира, отвеса и лазера изготовили высотомер.
Высота школы (без уровня глаз над землёй) = расстоянию от меня до школы умноженному на тангенс угла (по высотомеру).
Высота школы = 6,2+1,5 = 7,7 м.
Способ 10
При помощи тени школы и широты, на которой находится наше село.
Встанем перед школой в полдень Измерим длину тени, отбрасываемую школой L. L=5,62м. Т.к. наше село Подовинное находится на 54-й широте, =540
Ответ: H=7,73м
Способ 11.
При помощи фотографии.
Сделали несколько снимков, где я встала вплотную к зданию.
Измерили на фотографии высоту здания, и высоту мерки (меня).
Нашли отношение здания в мерках. И это отношение умножаем на рост «мерки». 4,7 *1,58 = 7,44 м
Способ 12.
При помощи тени.
Используя пропорцию:
Тень школы высота школы
=
Тень Тани рост Тани
Высота школы = 31,5*1,58:6,6=7,54 м
Способ 13.
При помощи тени шеста 1,5 м.
Используя пропорцию:
Тень школы высота школы
=
Тень рейки высота рейки
Высота школы = 31,5*1,5:6,2=7,6 м
Способ 14.
При помощи зеркала.
Узнав расстояние от «мерки» до зеркала, и от зеркала до школы – из подобия треугольников находим, что высота школы = 1789 *158 : 389 = 726,8см = 7,27м
Способ 15.
При помощи зеркала 1.
Встанем так, чтобы можно было видеть в зеркале верхний край крыши. Измерим расстояние между зеркалом и основанием стены
С помощью транспортира измерим угол. Из соотношения прямоугольного треугольника
H==3,6* 2,145 = 7,7м
Способ 16.
При помощи зеркала 2.
Используя теорему синусов:
, найдем
Ответ: H=7,7м
Способ 17.
При помощи зеркала 3.
- Установим зеркало на некотором расстоянии от стены и на произвольной высоте от земли так, чтобы в ней можно было видеть стену школы во ВСЮ высоту. Измерим с помощью линейки длину отражения стены h=0,36м.
- Установим линейку так, чтобы один ее конец почти соприкасался с глазом, а другой был направлен на отражение верхнего края стены. Измерим с помощью транспортира угол . Три отмеченных на рисунке угла равны, т.к. угол падения равен углу отражения .
- Установим линейку так, чтобы один ее конец почти соприкасался с глазом, а другой был направлен на отражение нижнего края стены. Измерим с помощью транспортира угол . Три отмеченных на рисунке угла равны, т.к. угол падения равен углу отражения .
- высоту школы вычислим по формуле
Ответ: H=7,95м.
Способ 18.
При помощи зеркала 4.
Встанем перед школой в полдень. С помощью зеркала M отбросим на верхний край стены школы солнечный зайчик. Замерим с помощью транспортира угол φ наклона зеркала к земле: φ = 45°. Мы уже применяли то соображение, что наше село Подовинное, где проводились измерения, находится на 54-ой широте, значит α, угол падения солнечных лучей, = 54°.
Способ 19.
При помощи зеркала 5.
Установим рейку длиной L (L = 1 м) перпендикулярно земле на расстоянии S от стены школы. На кончике рейки установим вертикально зеркало M. Возьмем другую рейку произвольной длины и наклоним её так, чтобы один её конец почти соприкасался с глазом, а другой был направлен на мнимое изображение в зеркале верхнего края стены. Два отмеченных на рисунке угла равны, так как угол падения равен углу отражения.
Очевидно, высота школы равна:
Способ 20.
При помощи рейки 40 см.
На уровне крыши на столбе возле здания нашей школы установлен фонарь. Данный эксперимент проводится вечером.
Дважды установим рейку перпендикулярно земле на разных расстояниях от школы и каждый раз измеряем длину тени, отбрасываемую рейкой.
Используя подобие треугольников, получим
Способ 21.
При помощи катушки ниток с грузом.
Возьмём катушку ниток, прикрепим к свободному концу мотка ниток груз, а катушку наденем на карандаш. Встав максимально близко к стене школы, бросим груз вертикально вверх. В момент достижения грузом стены школы на размотавшуюся нить наносим штрих маркером. После спуска конструкции измеряем с помощью рулетки длину нити от её кончика до ближнего к нему кончика метки. Оказалось, что H = 7,9 м.
Способ 22.
При помощи директора
Ну, а самым лёгким, доступным способом, несомненно, является наш последний способ: спросить у директора: « Какова же высота здания нашей школы по техническому паспорту?» Он то уж даст полный исчерпывающий ответ на наш вопрос. Оказалось, что высота равна 7,9 м.
Посчитав вот по этой формуле погрешность наших измерений, мы выяснили, что она составляет приблизительно 6%. А это даже меньше, чем мы предполагали вначале (10%).
Заключение
Оригинальность нашей работы была в создании лучшей модели измерения высоты здания, в интеграции предметов (физики и математики). Создав модель, и проводя эксперименты, мы более глубоко изучили подобие треугольников и применение подобия на практике; соотношения в прямоугольном треугольнике; более детально изучили некоторые физические явления (угол наклона, отвесы, механические и световые явления). То есть была доказана взаимосвязь теории с практикой.
Поэтому мы считаем, что наша гипотеза о том, что существует множество различных способов измерения высоты здания при помощи весьма незамысловатых приборов и даже без всяких приспособлений подтвердилась.
А
В
Тема «Измерение высоты здания школы различными способами»
Работу выполнили:
ученица 8 класса Филиппова Виоллета
ученица 8 класса Нильмаер Анна
Руководитель: учитель математики
Хоменко Ирина
Александровна
Цель исследования: измерить высоту здания различными способами без специальных приборов.
Задачи исследования:
- Проанализировать материал по проблеме исследования.
- Выяснить, какие существуют способы измерения высоты здания.
- Провести практические работы по измерению высоты школы разными способами.
- Оформить результаты в виде таблицы
Гипотеза исследования: предположим, что высоту здания школы, возможно, измерить без специальных приборов .
Методы исследования :
- Работа с источниками информации
- Организация практической работы
- Описание экспериментов
Способы определения высоты предмета
Метод Фалеса
Более распространенным способом является метод, с помощью которого еще Фалес, по преданию, измерил высоту египетских пирамид. Когда жрецы, желая испытать Фалеса, предложили учёному измерить высоту пирамиды, он дождался, когда длина его собственной тени стала равна его росту, и в этот момент измерил длину тени, которую отбрасывала пирамида. Эта измеренная длина тени и равна высоте пирамиды.
По шесту
- Взять шест, равный своему росту, и установить его на таком расстоянии от предмета (дерева), чтобы лёжа можно было видеть верхушку дерева на одной прямой с верхней точкой шеста. Высота дерева будет равна расстоянию от головы наблюдателя до основания дерева.
При помощи равнобедренного треугольника
Приближаясь к предмету (например, к дереву) или удаляясь от него, установить треугольник у глаза так, чтобы один из его катетов был направлен отвесно, а другой совпал с вершиной дерева. Высота дерева будет равна расстоянию до дерева (в шагах) плюс высота до глаз наблюдателя
С помощью зеркала (лужи)
На некотором расстоянии от измеряемого дерева, на ровной земле в точке кладут горизонтально зеркало и отходят от него назад в такую точку, стоя в которой наблюдатель видит в зеркальце верхушку дерева. Высота дерева, будет во столько раз больше роста человека, во сколько раз расстояние от него до зеркала больше, чем расстояние от зеркала до наблюдателя. Вместо зеркала можно использовать лужу.
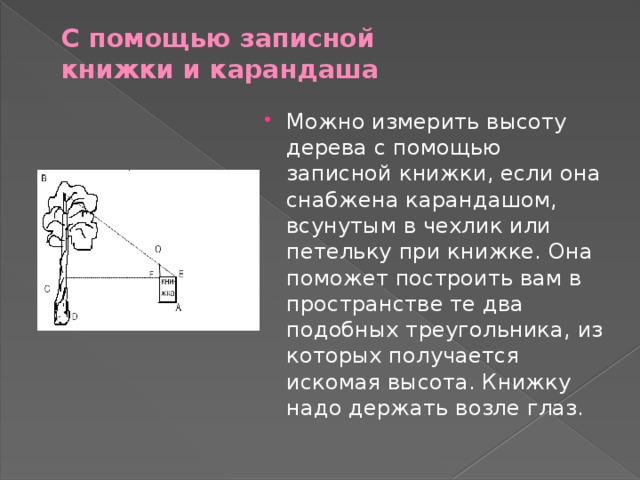
С помощью записной книжки и карандаша
- Можно измерить высоту дерева с помощью записной книжки, если она снабжена карандашом, всунутым в чехлик или петельку при книжке. Она поможет построить вам в пространстве те два подобных треугольника, из которых получается искомая высота. Книжку надо держать возле глаз.
исследование
Из всех перечисленных способов измерения высоты предмета, мы решили применить на практике – 1.Определение высоты школы по её тени;
2.По шесту 3.При помощи равнобедренного треугольника;
4.При помощи зеркала 5.Использовать фотографию здания школы.
По длине тени
Длина тени Ани – 2,3 м.
Длина тени школы равна 10,32 м.
Рост Ани – 1,56 м
Тогда высота школы :
H =
=10,32*1,56 :2,3=7, 0 м
В один из солнечных дней мы решили измерить высоту нашей школы способом Фалеса Милетского, то есть по длине тени, отбрасываемой зданием. Н – высота школы
С помощью шеста
В роли шеста была Аня ,
а в роли лежащего на земле
человека я.
Высота шеста – 1,56 м
Расстояние от макушки до школы – 8,53 м
Расстояние от макушки до шеста – 1,65 м
H =
Результат : Высота школы = 8,1 м
С помощью зеркала
Расстояние от школы до зеркала- 8,6 м
Расстояние от человека до зеркала – 1,72 м
Рост человека – 1,65 м
Рост человека до глаз -1,57 м
H =
Результат: Высота школы = 7,9 м
При помощи равнобедренного треугольника
Расстояние от школы до человека – 6,88 м
Рост человека до глаз – 1,48 м
Н = расстояние от школы до человека + рост человека до глаз
Н = 6,88+1,48=7,3 м
Результат: Высота школы = 7,3 м
С помощью фотографии
Высота школы на фото- 7,8 см
Мой рост – 1, 65 м
Мой рост на фото – 1,7 см
Н=
Результат:
Высота школы=7,6 м
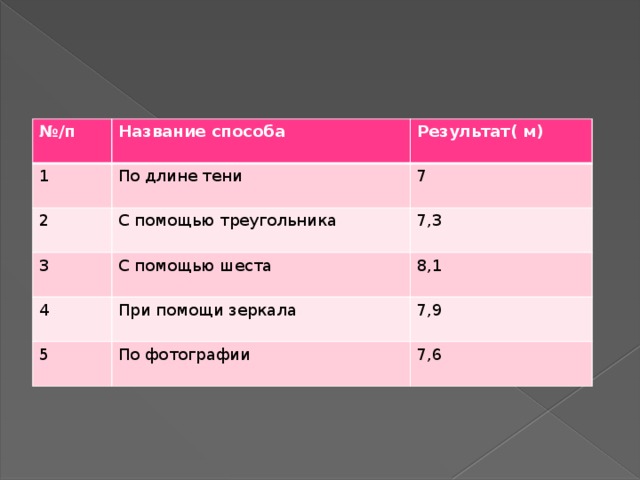
№ /п
Название способа
1
Результат( м)
По длине тени
2
С помощью треугольника
3
7
7,3
С помощью шеста
4
При помощи зеркала
8,1
5
7,9
По фотографии
7,6
Спасибо
за внимание!
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
«Кто с детских лет занимается математикой,
тот развивает внимание, тренирует свой мозг,
свою волю, воспитывает настойчивость и
упорство в достижении цели»
(А. Маркушевич)
Введение
Однажды в интернете я прочитала интересный случай о том, как один студент сдавал экзамен по физике. Преподаватель задал вопрос: “Объясните, каким образом можно измерить высоту здания с помощью барометра”.
Ответ студента был таким: “Нужно подняться с барометром на крышу здания, спустить барометр вниз на длинной веревке, а затем втянуть его обратно и измерить длину веревки, которая и покажет точную высоту здания”. После чего этот студент был выгнан из аудитории, но после подал на апелляцию, основываясь на том, что ответ был абсолютно правильным. На пересдаче студент заявил, что у него есть несколько решений проблемы, и он просто выбирал лучшее. И представил 25 решений этой задачи.
Студентом этим был Нильс Бор, впоследствии – великий датский физик, лауреат Нобелевской премии 1922г.
Актуальность темы:
В жизни иногда необходимо умение оценивать расстояние до предмета. Например, до леса, до другого берега реки, высоту скалы, дерева, здания. Каждому человеку, научившемуся писать и считать, неоднократно приходилось что-либо измерять. При этом не всегда под рукой мы имеем сантиметровую линейку или специальные приборы. Поэтому необходимо знать и косвенные методы измерения объектов, дающие неплохой результат. К тому жеповторение элементов алгебры и геометрии, таких как подобие треугольников и пропорция будет очень полезным.
Объект исследования:
высота здания Детчинской средней общеобразовательной школы
Предмет исследования: методы измерения высоты предметов
Цель – определить высоту здания средней общеобразовательной школы разными методами без специальных приборов
Задачи:
изучить интернет ресурсы и литературу по проблеме исследования;
провести анкетирование среди учащихся моего класса;
изучить различные методы измерения высоты зданий;
провести практическое исследование по измерению высоты школы разными способами;
найти наиболее точный способ измерения высоты зданий применимый на практике;
Гипотеза: предполагаю, что косвенные методы измерения дают близкие результаты к фактической высоте здания школы
На различных этапах моей исследовательской работы мною использовались следующие методы исследования: анализ литературы и материалов сети интернет, счет, измерение, сравнение.
Историческая справка:
Строительство современного здания школы начато в IV квартале 1975 года, окончено в конце 1977 года. Школа сдана в эксплуатацию с оценкой “Отлично”. Занятия в этом здании начались 11 января 1978 года.
Основная часть
1.Теоретическое исследование проблемы
1.1 Обзор литературы
Треугольники знакомы нам с детства. Эта геометрическая фигура таит в себе много интересного и загадочного. И чтобы измерить высоту школы мне пришлось повторить для своей работы такие понятиями как подобные треугольники, пропорция
Что такое подобные треугольники?
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Коэффициент подобия равен отношению сходственных сторон подобных треугольников.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобных треугольников.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Подобие треугольников в жизни.
Подобие треугольников можно применять для разных целей. Например, для измерения высоты дерева или дома.
Пропорция
Если у двух отношений одинаковое частное, то их можно соединить знаком равенства, тогда это равенство будет уже пропорцией.
Определение: Равенство двух отношений называется пропорцией.
Буквенная запись пропорции a:b = c:d — это общий вид пропорции, где:
a и d — это крайние члены пропорции; b и c — это средние члены пропорции.
Основное свойство пропорции: а*d = b*c
Правило 1. Произведение средних членов истинной пропорции равно произведению ее крайних членов.
Правило 2. Средние и крайние члены пропорции можно менять местами, от этого пропорция не изменится.
1.2 Описание методов измерения высоты предметов
При проведении исследования я познакомилась с различными методами измерения высоты зданий, их довольно много, но я выбрала наиболее простые и интересные для меня.
Метод при помощи фотографии
Надо сфотографировать человека возле здания. Человек должен стоять вплотную к измеряемому зданию. Затем надо узнать сколько раз человек может поместиться на фотографии вертикально. Это количество надо умножить на рост человека, это и будет высота здания.
Формула:
Н= Рост человека кол-во размноженных человек на фото
Метод при помощи шеста
П ри отсутствии тени в пасмурную погоду можно воспользоваться способом измерения, который был описан в книге Жюль Верна “Таинственный остров”.
Решение:
Нужно вбить в землю шест, лечь на землю так, чтобы было видно верхний конец шеста и верхушку измеряемого предмета. Измерить расстояние от шеста до предмета, измерить высоту шеста и расстояние от макушки человека до основания шеста.
Формула: H=
Припомощизеркала
Этот способ можно удачно применять после дождя, когда на земле появляются лужи.
Р ешение:
Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершина предмета. Измеряемый предмет, например, дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас. Вместо лужицы можно пользоваться положенным горизонтально зеркальцем.
Формула:
H =
Метод Фалеса (при помощи тени)
Как по длине тени, падающей от дерева в солнечный день, определить высоту дерева?
Решение: так как лучи солнца можно считать практически параллельными, то тень от дерева во столько же раз длиннее тени от какого либо шеста, во сколько раз дерево выше шеста. Поэтому, установив вертикально шестизвестной высоты и измерив отношение длины тени от дерева к длине тени от шеста, мы вычислим искомую (примерную) высоту дерева.
Формула:
H=
Более распространенным способом является метод, с помощью которого еще Фалес, по преданию, измерил высоту египетских пирамид. Когда жрецы, желая испытать Фалеса, предложили учёному измерить высоту пирамиды, он дождался, когда длина его собственной тени стала равна его росту, и в этот момент измерил длину тени, которую отбрасывала пирамида. Эта измеренная длина тени и равна высоте пирамиды.
При помощи воздушного шарика
Привязали нитку к шарику, размотали нитку до подъёма шарика до крыши школы. Смотали веревку и замерили ее длину.
Припомощи барометра
Барометр (с др.-греч. «тяжесть» и «измеряю») – прибор для измерения атмосферного давления. Ртутный барометр был изобретен итальянским математиком и физиком Торричелли в 1644 году, это была тарелка с налитой в неё ртутью и пробиркой (колбой), поставленной отверстием вниз. Когда атмосферное давление повышалось, ртуть поднималась в пробирке, когда же оно понижалось – ртуть опускалась. Из-за неудобства такая конструкция перестала применяться и уступила место барометру – анероиду, но метод, по которому такой барометр был изготовлен, стал применяться в термометрах. Барометр нужен для определения погоды и для определения высоты.
Припомощиравнобедренноготреугольника
Приближаясь к предмету (например, к дереву) или удаляясь от него, установить треугольник у глаза так, чтобы один из его катетов был направлен отвесно, а другой совпал с вершиной дерева. Высота дерева будет равна расстоянию до дерева (в шагах) плюс высота до глаз наблюдателя.
Практическое исследование проблемы
И зучив данные методы измерения я решила провести эксперимент: измерение высоты нашей школы перечисленными способами. Результаты представлены в рассчетной таблице.
Метод измерения с помощью фотографии.
Оборудование: фотоаппарат и программа Paint.
На этой фотографии я помещаюсь приблизительно 5,9 раз.
Мой рост равен 1 ,67 + 0,05=1,72
Результат: Н =5,9*1,72=10,1 м
Метод измерения с помощью шеста.
Пусть Н – это высота школы.
Оборудование: рулетка и шест.
В роли шеста была я, а в роли лежащего на земле человека мой одноклассник.
H=
Высота шеста – 1м 67 см
Расстояние от макушки до школы – 11,27м
Расстояние от макушки до шеста – 1,70 м
Высота школы-Н
Результат : Высота школы = 11м 07см
Метод измерения с помощью зеркала.
H =
Оборудование: зеркало и рулетка.
Расстояние от школы до зеркала- 23м
Мой рост – 1м 67 см
Мой рост до уровня глаз -1 м 57см
Высота школы – Н
Результат : Высота школы = 11м 64 см
Метод измерения при помощи тени.
Моя тень – 3,5м
Тень школы – 24,8м
Мой рост – 1,67м
Результат : Высота школы = 11м 83 см
Метод при помощи шарика
На мой взгляд, самый простой и веселый метод. Привязали нитку к шарику, размотали нитку до подъёма шарика до крыши школы. Смотали веревку и замерили ее размер. Высота школы получилась 11м 67 см.
Метод «Барометр»
С помощью барометра я измерила атмосферное давления на 1,2 и 3 этажах здания. Измерения высоты школы с помощью барометра – анероида не дал результатов – показания на улице и на третьем этаже школы были одинаковыми. По всей видимости, высота школы меньше 12 м.
Метод припомощиравнобедренноготреугольника
Удаляясь от здания школы, установили треугольник у глаза так, чтобы один из его катетов был направлен отвесно, а другой совпал с крышей школы. Высота школы равна расстоянию до школы плюс высота до глаз наблюдателя.
Мой рост до уровня глаз -1 м 57см
Высота школы – Н
Расстояние от меня до школы 10,5м
Результат: Высота школы 12,07м
Н=1,57+10,5=12,07м
3.Социальный опрос одноклассников
Я провела социальный опрос одноклассников по данной проблеме. Вопросы, на которые они отвечали:
Знаете ли вы, какова высота нашей школы?
Какая на ваш взгляд высота нашей школы?
Какой способ измерения высоты вы знаете?
Как, используя знания геометрии можно определить высоту удаленного предмета?
Как, используя знания физики определить высоту здания школы?
Результаты анкетирования
В опросе участвовало 20 учащихся 9б класса
Вывод:
Познакомившись с моим исследованием, многие ученики, на вопрос о необходимости изучать математику, ответят положительно. Моя работа может быть использована школьниками для повышения своего образовательного уровня, а также научит применять полученные в школе знания на практике, что сегодня очень актуально.
Заключение
В ходе исследования я изучила и проанализировала различную литературу и материалы сети интернет и выяснила, что существует много способов для измерения высоты различных предметов.
Измерение высоты школы я проводила 7 методами. Измерение высоты здания с помощью тени не всегда выполнимо, так как необходима солнечная погода. Методы дают примерно одинаковый результат.
Сравнив результат моих измерений с взятой информацией из Технического паспорта школы – 11,9м , можно прийти к выводу, что наиболее точным методом является «Метод измерения при помощи тени» и «Метод измерения при помощи равнобедренного треугольника» , но и остальные методы показали близкие результаты.
Конечно, измерение высоты удаленного предмета удобнее делать, когда в наличии имеется специальное измерительное оборудование. Но не каждый раз удается предугадать ситуацию, которая может возникнуть на прогулке или в туристическом походе. Вот тогда такие простые знания пригодятся и даже помогут выйти из затруднительного положения.
Оригинальность моей работы была в создании лучшей модели измерения высоты здания, в интеграции предметов (физики и математики). Создав модель, и проводя эксперименты, я более глубоко изучила подобие треугольников и применение подобия на практике; соотношения в прямоугольном треугольнике; более детально изучили некоторые физические явления (угол падения равен углу отражения). То есть была доказана взаимосвязь теории с практикой. По результатам измерений был проведен сравнительный анализ, составлены таблицы.
Гипотеза о том, что косвенные методы измерения высоты здания дают близкий результат подтвердилась. Таким образом, задачи исследовательской работы решены, поставленная цель достигнута, выдвинутая проблема выяснена.
Список используемой литературы
Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняков, И. И. Юдина. Геометрия. М. Просвещение. 2005г. 138с.
И. Баврин. Большой справочник школьника. Математика. М. дрофа. 2006г. 435с.
Сергеев И.Н., Олехник С.Н., Гашков С.Б. Примени математику. – М.: Наука. Гл. ред. физ.-мат. лит.,1989. – 240с.
газета: Гумеров И. Измеряем высоту // Математика №3, 2007.
газета: Каменева Т. Измерение высоты здания Пермэнерго // Физика в школе №9, 2008.
http://nsportal.ru/ap/library/drugoe/2013/03/21/izmerenie-vysoty-zdaniya-maksimalnym-kolichestvom-neobychnykh-sposobov
http://project.1september.ru/works/596940
https://ru.wikipedia.org
Приложение 1
Таблица «Измерение высоты школы»
|
Метод |
Формула |
Измерения(М) |
|
1.При помощи фото |
———————————————— |
Н= 10,1 |
|
2.При помощи шеста |
Формула: H= |
|
|
3.При помощи зеркала. |
H = |
|
|
4.При помощи тени. |
H= |
|
|
5. При помощи шарика. |
—————————————————- |
Н= 11,67м |
|
6 .При помощи барометра |
————————————————— |
Результат показал Н меньше12м |
|
7.При помощи равнобедренного треугольника |
Н=рост человека до глаз+расстояние от челов.до здания |
Н=1,57+10,5=12,07м |
|
№ |
Метод |
Результат |
Ошибка |
|
1 |
По фотографии |
11,52м |
3% |
|
2 |
При помощи шеста |
11,07м |
7% |
|
3 |
Припомощизеркала |
11,64м |
2% |
|
4 |
При помощи тени |
11,83м |
0,5 % |
|
5 |
При помощи шарика |
11,67м |
2% |
|
6 |
Припомощи барометра |
меньше 12м |
|
|
7 |
При помощи равнобедренного треугольника |
12,07 |
1,4 % |
Приложение 2
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5