Как найти высоту сооружения

Для
определения высоты сооружения, например,
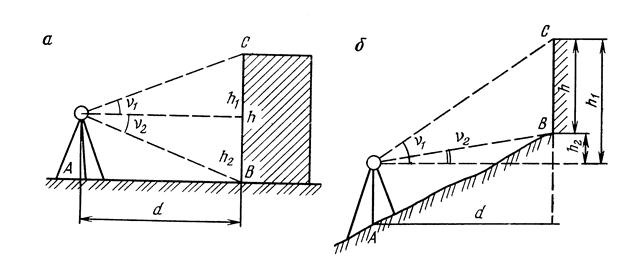
здания (рисунок 66, а) в точке А,
расположенной вблизи здания, устанавливают
теодолит и измеряют углы наклона ν₁
и ν₂
, визируя на верхнюю и нижнюю точку
здания. Измеряют расстояние АВ
= d
и определяют высоту здания

или

(66)

Рисунок
66- Схемы определения высоты сооружения

Если
линия местности АВ
наклонна (рисунок 66, б), то нужно измерить
ее наклон и вычислить горизонтальное
проложение d.

Из
рисунка 66, б следует, что высота здания
равна

или

(67)

В
формуле (67) углы наклона ν₁
и ν₂
положительные.

Если
в формуле (66) учесть знак минус угла
наклона (рисунок 66,а), то формула (66)
будет иметь вид (67) и будет универсальной.

В
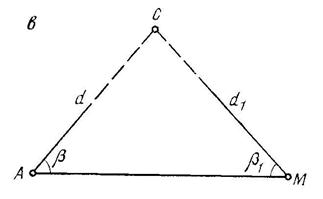
том случае, когда измерить расстояние
от теодолита до сооружения нельзя, его
определяют как неприступное расстояние,
для чего в стороне от сооружения
разбивают базис АМ
(рисунок 66, в).

Теодолитом
измеряют горизонтальные углы β
и β₁
и вычисляют длины линий

(68)

В
точках А
и М
измеряют вертикальные углы соответственно
ν₁
, ν₂
и ν₃,
ν₄.
Высоту
сооружения вычисляют дважды

(69)

В
формулах (69) следует учитывать знак
угла наклона; за окончательное значение
h
берут среднее, если расхождение не
более 1: 300 высоты измеряемого сооружения.

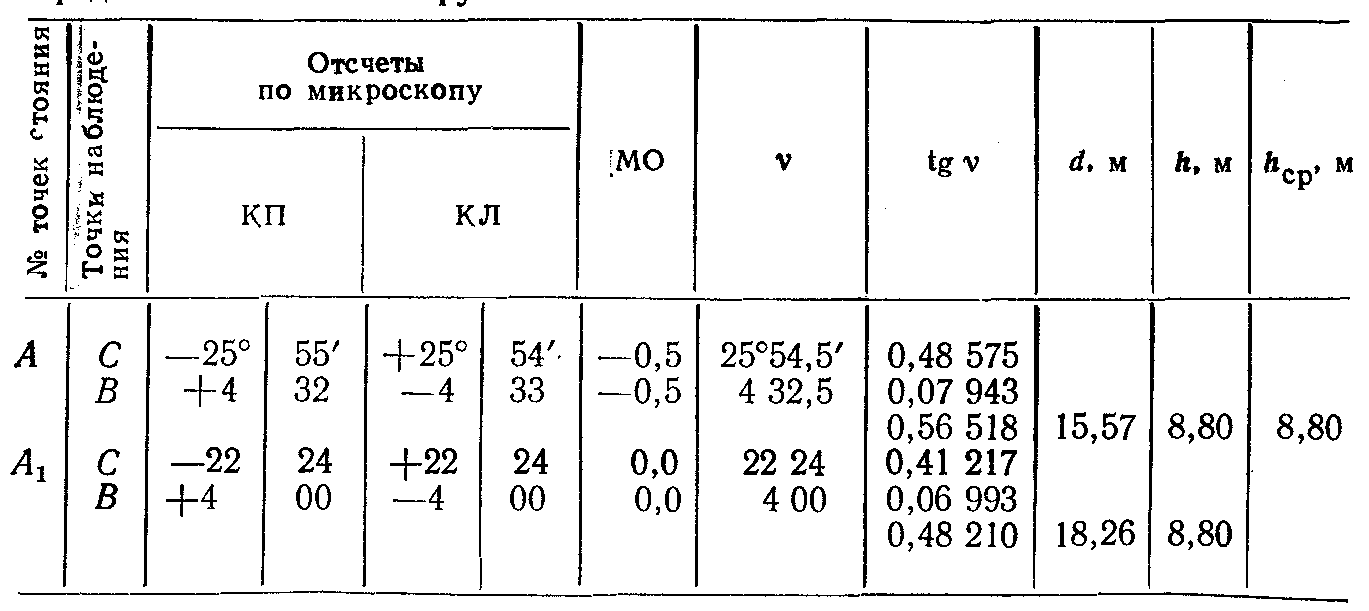
Пример
определения высоты сооружения приведен
в таблице 22. Углы наклона измерялись
теодолитом 2Т30.

Таблица
22 – Определение высоты сооружения

ЛЕКЦИЯ
20

20.1 Геодезические работы в процессе строительства. Детальная

разбивка
зданий и сооружений

Детальная
разбивка
выполняется после
вынесения
на мест­ность основных
осей зданий или
сооружений.
Основными
ви­дами
геодезических
работ
при
детальной разбивке
являются следующие:

1.
Разбивка котлованов и траншей для
проведения земля­ных работ.

2. Разбивка
осей для возведения фундаментов.

3.
Разбивка осей для монтажа строительных
конструкций и геодезический контроль
за установкой конструкций в проект­ное
положение.

Точность
выполнения геодезических работ при
детальной разбивке зависит от типа
сооружения, этажности, высоты со­оружения,
материала возведения, технологических
особенностей производства и
регламентируется строительными нормами
и правилами СНиП 3.01.03—84 «Геодезические
работы в строи­тельстве», а также
ГОСТами «Система обеспечения точности
геометрических параметров в строительстве».
Вследствие того, что оси детальной
разбивки определяют взаимное положение
различных конструкций, к точности их
разбивки предъявляют более высокие
требования, чем к разбивке основных
осей, оп­ределяющих положение всего
здания или сооружения на мест­ности.
В зависимости от требуемой точности
выбираются при­боры и способы
геодезических разбивочных работ.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как определить высоту здания

Высоту любого объекта можно довольно точно замерить прибором, называемым высотомером. Можно влезть на крышу здания и замерить его высоту рулеткой, спустив ее вниз. Однако если вам требуется узнать высоту здания лишь однажды и с невысокой точностью – например, чтобы убедиться, что соседний дом не заслоняет сигнал со спутника, который вы хотите принимать на спутниковую антенну – нет резона покупать дорогостоящий прибор или влезать на крышу. Существуют иные способы определения ориентировочной высоты зданий.

Вам понадобится

• Рулетка, калькулятор.

Инструкция

Определение высоты стандартных многоэтажных зданий
Посчитайте количество этажей в здании. Умножьте полученное число на 2,9 м и прибавьте к произведению 1,5 и 2 м. Полученное значение будет примерно равно высоте здания. Указанные цифры означают:
• 2,9 м – средняя высота этажа;
• 1,5 м – высота полуподвала;
• 2 м – высота чердака.

Определение высоты здания с помощью его тени
В солнечный день выберите на здании две контрольные точки: верхнюю (на самом верху здания) и нижнюю (на земле у основания здания). Нижняя точка должна располагаться на одной вертикали с верхней. Проще всего за контрольные точки принять верх и низ угла дома, если он отображается на тени.
Отыщите на тени дома верхнюю контрольную точку. Измерьте расстояние от нее до нижней контрольной точки здания. Обозначьте это значение буквой M.
Воткните в землю в любом освещенном солнцем месте шест длиной 1,5-2 м. Замерьте длину его тени. Обозначьте длину шеста и длину его тени как h и m соответственно.
Определите высоту здания по формуле H=(h*M)/m в метрах.
Формула основана на подобии треугольников, один из которых образуется двумя контрольными точками здания и тенью верхней контрольной точкой, а другой – шестом и его тенью.

Определение высоты здания с помощью картонного треугольника
Вырежьте из картона или ДВП прямоугольный треугольник с равными катетами (половина квадрата). Катет может быть любым, например, 0,5 м.
Глядя на верхнюю контрольную точку здания через гипотенузу треугольника (так, чтобы ваш глаз, гипотенуза треугольника и верхняя контрольная точка находились на одной линии) – отступайте от здания до тех пор, пока катет треугольника (дальний от вас) не займет вертикальное положение. Отметьте это место каким-нибудь предметом – например, камнем.
Замерьте расстояние от найденной точки до нижней контрольной точки здания. Прибавьте к этому земли. Полученное значение будет равно высоте здания.
Для удобства измерений желательно иметь помощника, который будет контролировать перпендикулярность катета треугольника отвесом. Можно также треугольник прибить к шесту таким образом, чтобы его катет был параллелен шесту. Сохранять вертикальное положение шеста, упертого в землю, намного проще, чем контролировать положение треугольника.
Как и в предыдущем случае данный способ основывается на подобии треугольников – картонного и образованного соединением трех точек – вашего глаза, верхней и нижней контрольных точек здания.

Обратите внимание

При определении высоты здания с помощью треугольника точность измерения определяется размерами треугольника, чем они больше, тем точнее получается найденное значение.

Источники:

• как найти высоту здания

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Определение высоты сооружения

Одной из распространенных и важных задач геодезии представляется задача измерения высоты здания или сооружения. На местности эти работы можно выполнить с помощью теодолита и мерной ленты. Теодолит располагают вблизи здания или сооружения так, чтобы можно было измерить расстояние от точки установки теодолита до стены здания, а также определить соответствующие углы наклона визирной оси теодолита.

Рис. Схемы определения высоты сооружения.

Определив расстояние АВ = d, с помощью тригонометрических функций определяют высоту здания по формуле:

В случае, если на местности линия АВ имеет уклон, то необходимо рассчитать горизонтальное проложение данной линии, то есть её проекцию на горизонтальную плоскость. При расчетах необходимо учитывать знак углов наклона соответствующих линий υ₁ и υ₂.

Иногда бывает невозможно непосредственное измерений расстояния от теодолита до сооружения. В этом случае соответствующее расстояние может быть определено на местности с помощью известных приемов. Например, в стороне от сооружения следует разбить базис АМ. Далее измерить горизонтальные углы β₁ и β₂, после чего рассчитать расстояния d и d₁

В точках А и М необходимо определить последовательно вертикальные углы и вычислить высоту сооружения по данным точки М и точки А. За окончательное значение высоты здания принимают среднее арифметическое из двух полученных значений, если расхождение между ними не превышает 1:300.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

51.Определение высоты недоступного сооружения.

Работа выполняется с помощью теодолита, мерной ленты или рулетки. Для этого необходимо на местности разбить базис d такой длины, чтобы его конечные точки M и N отстояли от основания определяемого предмета, примерно, в полуторной высоте этого предмета, и угол b₃ (β3)в вершине с недоступным предметом (мачты) «О» был не менее 30 0 .

Базис d измеряется дважды с относительной погрешностью 1/2000. С концов базиса M и N измеряются полным приемом горизонтальные углы b ₁ и b₂, вертикальные углы n₁ и n₂ при точке N и n₃ и n ₄ – при точке М, наведением зрительной трубы на верхнюю точку А и основание предмета (мачты) О. Отсчет по вертикальному кругу при наблюдении верхней точки и основания предмета производится при КЛ и КП.

Обработка наблюдений начинается с определения горизонтальных расстояний d1 и d2 по формулам:

,

Углы наклона определяются по известной формуле вертикального круга для теодолитов типа 2Т30, то есть

Полная высота предмета (мачты) Н определяется из формулы:

.

Вычисленные значения высоты предмета Н по обеим формулам могут различаться в пределах 2–3 см. За окончательное значение высоты предмета принимается среднее арифметическое из полученных значений.

52.Основные сведения о геодезических сетях и методах их создания.

Геодезическая сеть — это группа зафиксированных на местности точек, для которых определены плановые координаты (X и Y) в принятой двухмерной системе координат

Принцип построения геод. сетей:

от общего к частному

от больших расстояний к меньшим расстояниям

от более точных измерений к менее точным.

Методы построения геодезических сетей:

1. Триангуляция- создается путем построения на местности простых фигур, чаще всего – треугольников. Во всех треугольниках измеряются горизонтальные углы; сторону АБ измеряют светодальномером или радиодальномером. Затем по теореме синусов вычисляют стороны треугольников, после решают прямую геодезическую задачу.

2. Трилатерация –измерение всех сторон светодальномером или радиодальномерами. Вычисляют горизонт углы. Последующие вычисления смотри метод триангуляции.

Методы триангуляции и трилатерации целесообразно использовать на открытых территориях (степь, пустыня, залесенная территория (над пунктом строится сигнал)).

3.Полигонометрия –универсальный метод используется как на открытой местности, так и на закрытой (в городах). Измеряют горизонт углы и стороны. От дирекционного угла αА-Б стороны АБ переходят к дирекционному углу αА-1 стороны А1. По известному дирекционному углу и измеренным горизонтальным углам можно вычислить дирекционные углы сторон. Зная α и d (длину стороны) можно вычислить координаты искомых точек.

53.Плановое обоснование топографических съемок. Полевые работы. Требования,

предъявляемые к проложению теодолитных ходов.

Создается с целью обеспечения всех съёмок и всех стадий проектирования. Плановое обоснование может быть в виде замкнутого и разомкнутого теодолитного хода, системы теодолитных ходов с угловыми точками.

Полевые работы при создании планового съемочного обоснования: 1)Рекогносцировка местности; 2)Измерение ходов полным приемом теодолитом с технической точностью; 3)Измерение длин сторон (с относительной ошибкой не грубее 1/2000, лентами и рулетками); 4)Камеральная обработка результатов.

Согласно ГОСТу выпускают три типа реек: РН-05, РН-3, РН-10

РН-05 – штриховая трёхметровая рейка с инварной полосой, на которую нанесены основная и дополнительная шкала с делениями 5 мм., предназначены для нивелирования 1 и 2 классов и высокоточного нивелирования в прикладной геодезии.

РН-3, РН-10 – сантиметровые, шашечные, двусторонние, 3 и 4-метровые рейки, целые или складные. РН-3 используют при нивелировании 3 и 4 классов.

Источник

Решение некоторых инженерных задач

Определение неприступного расстояния

Неприступное расстояние – это расстояние до объекта, находящегося в поле зрения наблюдателя, которое не может быть измерено непосредственно. Это чаще всего связано с наличием на местности каких-то препятствий (забор, водоем и т.п.). В таком случае прибегают к косвенному способу измерений, когда измеряются какие-то дополнительные величины (линейные или угловые), а искомое расстояние вычисляется с их помощью.

Неприступное расстояние определяют, как правило, из системы двух треугольников, построенных на основе измеренных базисов. Базисы разбивают на слабопересеченной местности, длина их должна быть не менее половины измеряемого расстояния. Базисные расстояния измеряют лентой или рулеткой с точностью 1/2000–1/3000, углы – теодолитом полным приемом. Схема определения неприступного расстояния показана на рис. 1.1.

Рис. 1.1. Схема определения неприступного расстояния и высоты сооружения

Из решения треугольников ABCиADCопределяют неприступное расстояние по формулам:

; (1.1)

. (1.2)

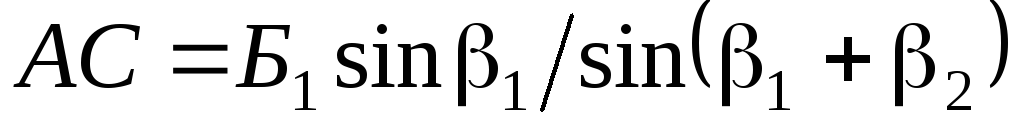
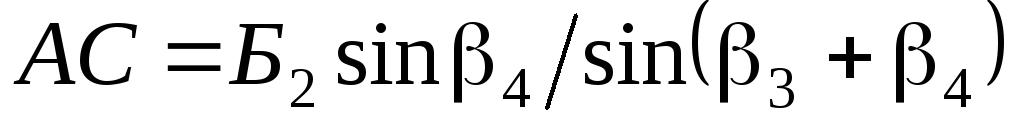
Относительная погрешность двух вычисленных значений неприступного расстояния не должна превышать 1/1000. При этом условии неприступное расстояние принимается равным среднему арифметическому двух вычисленных.

Например, м,м,,,,. Вычисляем неприступное расстоянием;м. Среднее значение неприступного расстояниям.

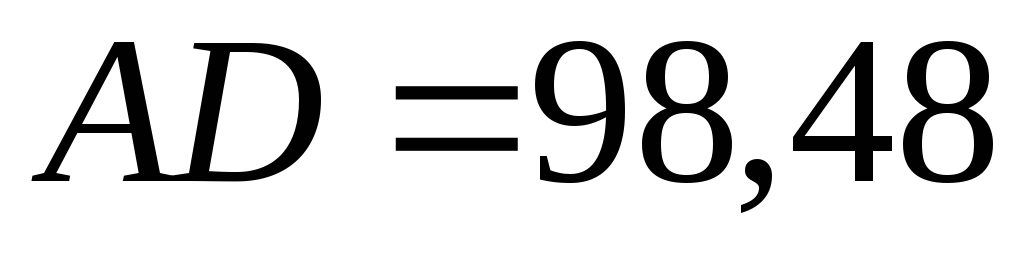
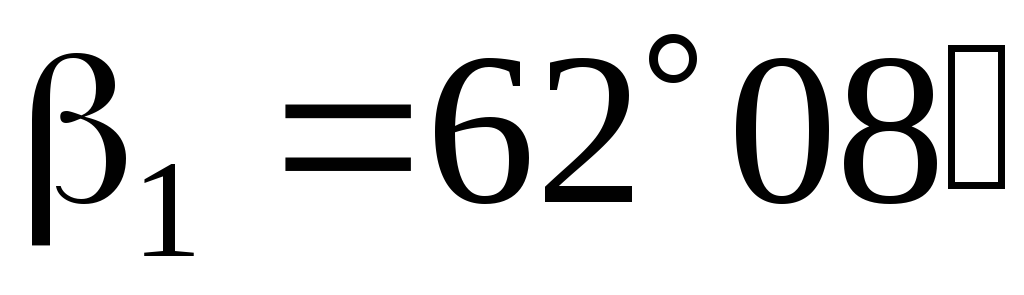
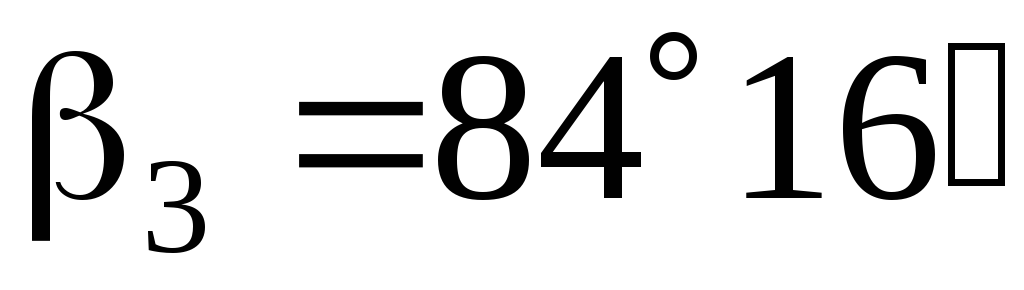
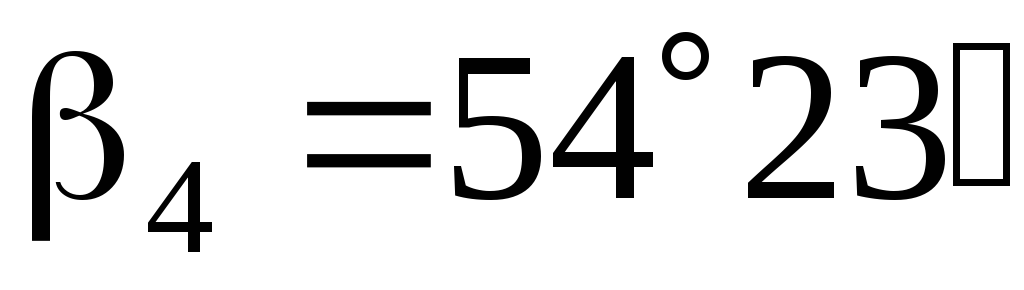
Определение высоты сооружения

Для определения высоты сооружения башенного типа на некотором расстоянии от него в точке D устанавливают теодолит и измеряют вертикальные углы ипри двух положениях вертикального круга: КЛ и КП (см. рис. 1.1).Тогда высота сооружения равна:

, (1.3)

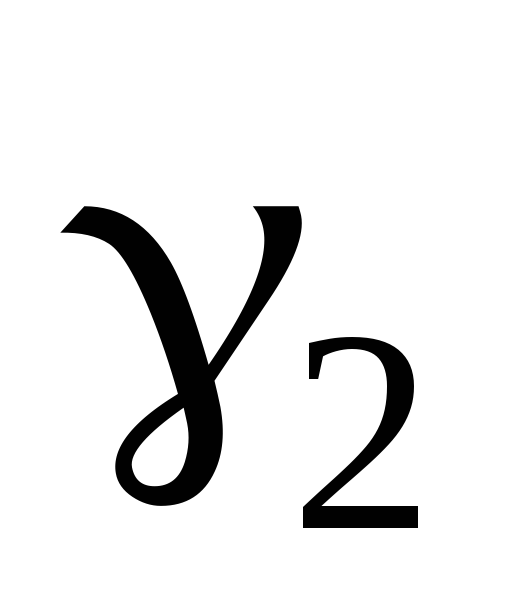
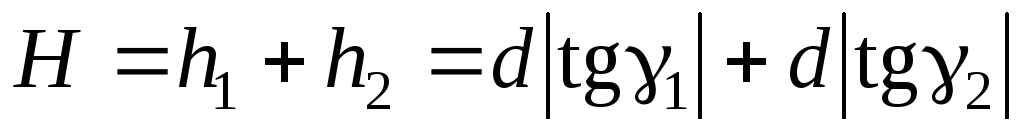
где d – горизонтальное проложение линии, которое может быть измерено лентой, рулеткой или дальномером. При невозможности непосредственного измерения линии ее вычисляют как неприступное расстояние, разбив предварительно базисы.

Для контроля проводят такие же измерения и вычисления с точки B(см. рис. 1.1). Например,

м,,.

м;

м;

м.

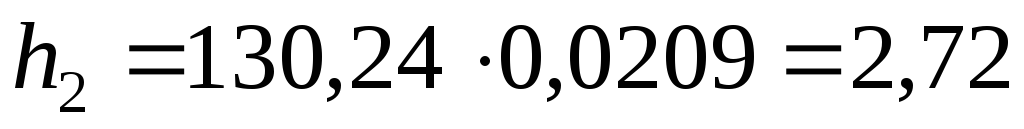
Аналогично обрабатывают результаты измерений со станции на точке B.

Наблюдения за креном сооружения

Общие сведения

Креном называется отклонение сооружения от проектного положения в вертикальной плоскости. Причиной его возникновения обычно является неравномерная осадка основания сооружения. Геометрическая сущность измерения крена сводится к определению взаимного положения двух точек сооружения (например, точки A и B на рис.1.2), которые по техническим условиям проекта должны лежать на одной отвесной линии. Наиболее простым способом полная угловая величина крена  может быть получена проецированием точки A на горизонтальную плоскость. Измерив высоту h точки A и длину проекции l, можно найти

. (1.4)

Рис. 1.2. Определение крена сооружения

Другим способом определения крена угла здания является способ горизонтальных углов, при котором с опорных пунктов, расположенных на взаимно перпендикулярных осях, измеряют горизонтальные углы между опорным направлением и направлениями на верхнюю и нижнюю точки угла здания. По разнице измеренных углов и горизонтальному проложению от станции до наблюдаемой точки находят составляющие крена по осям и полную величину крена.

Источник

19.8 Определение высоты сооружения

Для определения высоты сооружения, например, здания (рисунок 66, а) в точке А, расположенной вблизи здания, устанавливают теодолит и измеряют углы наклона ν₁ и ν₂ , визируя на верхнюю и нижнюю точку здания. Измеряют расстояние АВ = d и определяют высоту здания

или 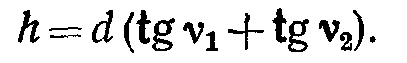(66)

Рисунок 66- Схемы определения высоты сооружения

Если линия местности АВ наклонна (рисунок 66, б), то нужно измерить ее наклон и вычислить горизонтальное проложение d.

Из рисунка 66, б следует, что высота здания равна

или (67)

Если в формуле (66) учесть знак минус угла наклона (рисунок 66,а), то формула (66) будет иметь вид (67) и будет универсальной.

В том случае, когда измерить расстояние от теодолита до сооружения нельзя, его определяют как неприступное расстояние, для чего в стороне от сооружения разбивают базис АМ (рисунок 66, в).

Теодолитом измеряют горизонтальные углы β и β₁ и вычисляют длины линий

(68)

(69)

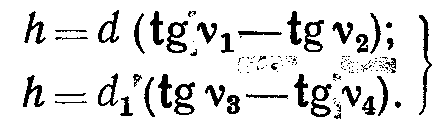
В формулах (69) следует учитывать знак угла наклона; за окончательное значение h берут среднее, если расхождение не более 1: 300 высоты измеряемого сооружения.

Пример определения высоты сооружения приведен в таблице 22. Углы наклона измерялись теодолитом 2Т30.

Таблица 22 — Определение высоты сооружения

20.1 Геодезические работы в процессе строительства. Детальная

разбивка зданий и сооружений

Детальная разбивка выполняется после вынесения на мест­ность основных осей зданий или сооружений. Основными ви­дами геодезических работ при детальной разбивке являются следующие:

1. Разбивка котлованов и траншей для проведения земля­ных работ.

2. Разбивка осей для возведения фундаментов.

3. Разбивка осей для монтажа строительных конструкций и геодезический контроль за установкой конструкций в проект­ное положение.

Точность выполнения геодезических работ при детальной разбивке зависит от типа сооружения, этажности, высоты со­оружения, материала возведения, технологических особенностей производства и регламентируется строительными нормами и правилами СНиП 3.01.03—84 «Геодезические работы в строи­тельстве», а также ГОСТами «Система обеспечения точности геометрических параметров в строительстве». Вследствие того, что оси детальной разбивки определяют взаимное положение различных конструкций, к точности их разбивки предъявляют более высокие требования, чем к разбивке основных осей, оп­ределяющих положение всего здания или сооружения на мест­ности. В зависимости от требуемой точности выбираются при­боры и способы геодезических разбивочных работ.

Источник

Приветствую Вас, уважаемый читатель!

Как-то в юности я занимался альпинизмом и ориентированием на местности, и не знаю как сейчас, но в то время нужно было обязательно знать раздел “Выживание в экстремальных условиях”, чтобы сдать экзамен и получить какой-либо разряд!

Собственно, решил поделиться с Вами и написать вкратце данную статью, полагая, что это будет очень познавательно и интересно! На самом деле способов еще гораздо больше, чем описано здесь, но они практически схожи, и вы в процессе чтения, вникнув в суть – сможете сами моделировать ситуации, и понять, что всё не так уж и сложно.

Ну что же, поехали…

Конечно не часто, но бывают в нашей жизни ситуации и обстоятельства, когда нужно знать высоту или расстояние до какого-либо объекта, например дома, дерева, да или похвастаться перед подругой))). Возможно придется строить траекторию для установки спутниковой тарелки, чтобы сигнал “стрелял” обходя высотки и не мешали кроны деревьев… ))) А мало ли, что еще…

Как ни парадоксально, но не забираясь с рулеткой на объект – расчет сделать не сложно, при том, что каждый метод может дать довольно точный результат. Конечно, с точностью до миллиметров не вычислить искомое значение, но погрешность будет точно уж небольшой.

Высота по отбрасываемой тени

Если погода солнечная и четко прослеживается тень, выбираем на объекте нижнюю контрольную точку от которой берет начало отбрасываемая тень будь-то дома, дерева, столба и пр.

Далее, ищем конец тени и производим замер длины тени.
После чего фиксируем в вертикальном положении любой предмет (на фото ниже – это обычный колышек) и аналогично замеряем длину его тени, а потом еще и высоту от точки начала тени до верхушки предмета.

Надеюсь, что у вас нет сомнения, что на фотографии треугольники с катетами Х1, Y1 и X2, Y2 подобны? Расчет строится на геометрическом свойстве подобных треугольников в которых отношения сторон равны и искомая высота объекта Y1 находится так:

Y1 (Высота столба) = (Y2*X1) / X2

Подручный предмет

Здесь требуется отойти от объекта и с помощью подручного предмета на вытянутой руке (ручки, карандаша, палки) замерить высоту. Конец предмета должен совпасть с верхней точкой объекта, а нижнюю точку требуется зафиксировать большим пальцем руки.

Разверните предмет горизонтально так, чтобы низ его по-прежнему оставался у основания объекта, а кончик касался земли и указывал на определенную точку. Важно запомнить эту точку или, если есть помощник, попросить встать на эту точку. Как раз эта точка будет являться точкой проекции верхушки на землю и теперь остается только замерить расстояние.

Угол падения и угол отражения

А если солнца нет и идет дождь, тоже не беда!

Согласно закону преломления из физики, о том что угол падения равен углу отражения – в зеркальном отражении любой лужи вы можете найти верхушку объекта и зная свой рост и расстояния соответственно, – получить искомую высоту (см.рисунок ниже).

Зафиксируйте точку О любым предметом, брошенным в лужу. Таким образом вы сможете измерить расстояния ОА, ОА1.

Зная все необходимые величины и основываясь на свойствах подобных треугольников, получите высоту, которая будет равна:

АВ = (А1В1 * ОА) / ОА1

Барометр и немного юмора

Нам понадобится немного знаний физики. Из школьного курса известно, что атмосферное давление зависит от высоты над уровнем моря и измерив давление у основания объекта и на вершине – можно вычислить расстояние подъема.

Средняя величина уменьшения атмосферного давления составляет 1 мм. рт. столба на каждые 12 м. высоты или 133,32 Па (Паскаль), что – то же самое. Поэтому, независимо от того, в каких единицах получено значение давления – вы всегда сможете посчитать высоту.А если у вас есть секундомер (он есть в каждом телефоне), то сбросьте барометр с высоты, при этом засекая время его падения )))))).

Путь, пройденный телом в свободном падении равен:

S = (g*t^2)/2, где:

g – ускорение свободного падения – 9.8 м./с^2;

t – время по секундомеру, с.

Определяем высоту объекта на расстоянии от вас

Для определения высоты нам в любом случае требуется расстояние до объекта, но основание его нам не доступно, – по-этому измерение нельзя произвести непосредственно.

Чтобы вычислить расстояние, нам нужно:

1. Остановиться напротив объекта и зафиксировать эту точку (На рисунке точка А).
2. Повернуться под прямым углом (на 90 град.) и сделать несколько шагов. Эта точка будет являться точкой О (здесь нужно воткнуть длинный предмет, например палку).
3. Пройти то же расстояние, что и от А к О, и в том же направлении. Отметить каким-либо предметом (точка В).
4. Повернуться под прямым углом (на 90 град.) и удаляться от объекта (в сторону точки Y) до тех пор, пока установленный ваш предмет в точке О не будет совмещен с объектом.
5. Расстояние от вас (Y) до точки В – это и есть расстояние от точки А до объекта (Х).

Теперь, зная расстояние до объекта, переходим к вычислению его высоты.

Для простоты построения опять же подобных треугольников – берется шест с подвижной планкой (две доски сбиваются гвоздем). Устройство фиксируется в точке А, планка настраивается (при помощи врожденного глазомера в каждого из нас) на верхнюю точку объекта (Х1) – как показано на иллюстрации, после чего фиксируется.

Далее, отмечается на земле точка С.

В итоге мы получаем два треугольника СХХ1 и САА1, которые подобны между собой. Зная расстояние ХС, АС и АА1 находим искомую высоту Н объекта!

Высота Н = (АА1 * ХС) / АС.
____________________

Если Вам было интересно, ставьте палец вверх и подписывайтесь на канал!

1. Если диагонали равны, то это не значит, что у вас ровный дом. Почему? Рассказываю историю!

2. Почему основной типоразмер изделий металлопроката составляет в длину 11,7 м.?

3. Варианты построения прямых углов при строительстве дома и проверка углов при уже возведенном сооружении.