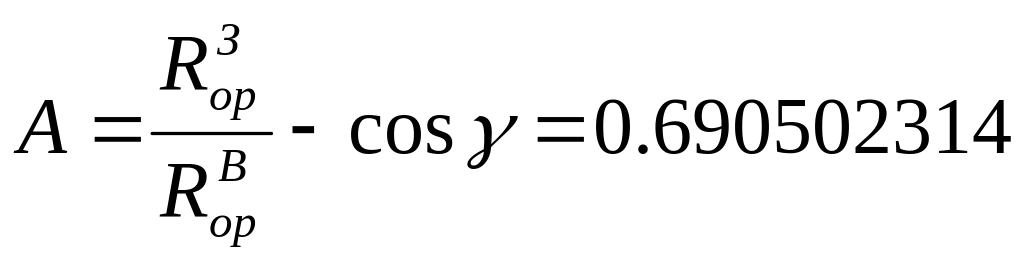Высота орбиты
спутника
Следующая
задача,
которую рассмотрим, состоит в определении высоты орбиты
спутника h над поверхностью Земли, если известны масса М≈5.96*1024 (кг) и радиус R≈6.37*106 (м) Земли, масса спутника
m, период его обращения Т.
Масса спутника в данном случае при расчете высоты орбиты не нужна, а
период обращения вводится пользователем. При решении этой задачи
воспользуемся тем, что сила гравитационного притяжения между Землей и
спутником равна F=GmM/(R+h)2, где G≈6.672*10-11(Нм2/кг2)
–
универсальная гравитационная постоянная.
С другой стороны, эту же силу по второму закону Ньютона можно записать
как F=ma, где а=ω2(R+h) есть центростремительное ускорение,
а частота ω связана с периодом Т соотношением ω=2п/Т. Из этих
соотношений получаем 4п2m(R+h)/T2=GmM/(R+h)2,
что
дает h=(GMT2)1/3*/4п2-R. Соответствующий
программный код приведен в листинге 1.12
==========>Листинг 1.12 Высота
орбиты
спутника
#include<iostream>
#include <cmath>
using namespace std;
int main(){
//Гравитационная постоянная:
const double G=6.672E-11;
//Масса Земли:
const double M=5.96E24;
//Радиус Земли:
const double R=6.37E6;
//Число pi:
const double pi=3.1415;
//Период и высота орбиты:
double T,h;
//Ввод периода (в часах):
cout<<“Введите T = “;
cin>>T;
//Перевод часов в секунды:
T=T*3600;
//Определение высоты:
h=pow(G*M*T*T/4/pi/pi,(double)1/3)- R;
//Перевод в километры:
h=h/1000;
cout<<“Высота орбиты спутника h = “<<h<<” kmn”;
cout << “Конец задания для самостоятельной работы!” << endl;
system
(“pause”);
//
ожидаем нажатия кнопки
return 0;
}
==========>Конец Листинга 1.12 Компилированный
исполняемый
файл листинга 1.12(120Кб, rar)
Результат выполнения программы может выглядеть следующим образом(жирным
выделен ввод пользователя)
Введите T = 5.4
Высота орбиты
спутника h = 9244.22 km
В программе использована встроенная функция pow() для вычисления
кубического корня. Первым аргументом функции указывается возводимое в
степень выражение, второй её аргумент – степень, в которую возводится
выражение. В данном случае степень равна 1/3.
Однако в силу автоматического преобразования типов при вычислении
выражения 1/3 используется целочисленное деление, в результате чего
получаем ноль. Чтобы избежать такой неприятности, во втором аргументе
функции
pow()
использована инструкция (double) для
выполнения явного приведения типов.
Обращаем также внимание читателя на способ ввода больших чисел: они
вводятся в формате мантиссы и показателя степени. Например,
число(литерал) 6.672*10-11 вводится
как
6.672E-11, а
число 5.96*1024 – как 5.96E24
* Математическое выражение
вида (х)1/3 –
“х
в степени одна третья” эквивалентно выражению “кубический корень из
х”, здесь применяется запись такого вида поскольку в Html нет символа
выражающего корень энной степени в привычном школьном выражении.
Гуру
(2967),
закрыт
12 лет назад
Александр Белик
Мастер
(1831)
12 лет назад
Во-первых, наверно, все же 4 км/ сек. Нет? :-)))
“Космические скорости.
Первая космическая скорость, или круговая скорость V1 – скорость, необходимая для обращения спутника по круговой орбите вокруг Земли или другого космического объекта. Если R – радиус орбиты, а G – гравитационная постоянная, то V1 = (GM/R)1/2. Для Земли V1=7.9 км/с. ..”
Тогда V1^2 / V^2 = R / R1 (здесь R – искомый радиус орбиты, R1 – радиус Земли.
Отсюда R = R1 * V1^2 / V^2 = 6,37·10^6 (м) * (7,9^2 / 4^2) = 24 846 981 (м) = 24 850 (км)
Тогда высота = 24 850 – 6 370 = 18 480 (км)
-
Определение высоты стационарного спутника.
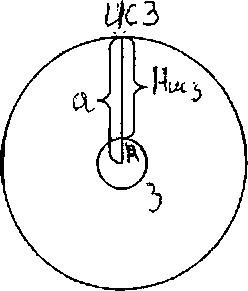
В зависимости от
J
спутники делятся на:
J=90˚
– полюсные
J=0˚
-экваториальные
0˚<J<90˚
– наклонные
Стационарным
называется спутник, который постоянно
находится над одной и той же точкой
Земли. Это возможно если орбита спутника
расположена в плоскости экватора и
период обращения спутника равен периоду
обращения Земли вокруг своей оси.
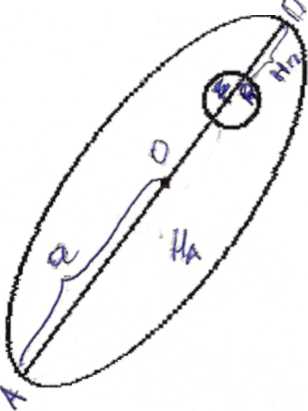
H
– высота ИСЗ над поверхностью Земли;
а – большая полуось
орбиты ИСЗ;
R=6378.211
км;
Т – период обращения
ИСЗ;
Μ = 3,9806∙105
км3/с2
км
Hисз=a-R=42221.996-6378.211=35843.785
км
-
Вычисление некоторых параметров исз.
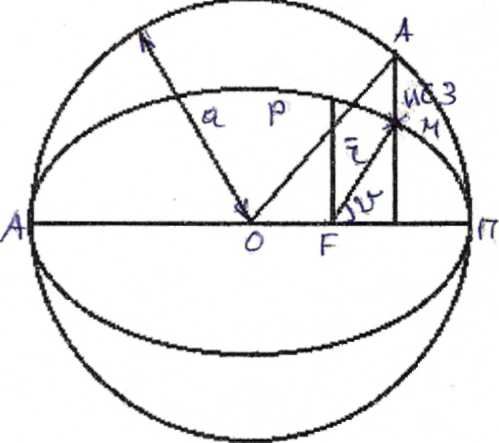
HП
– высота перигея;
E
– эксцентрическая аномалия;
HA
– высота апогея;
-радиус-вектор ИСЗ;
АП – линия апсид;
P
– фокальный параметр;
-истинная
аномалия;
R=6378211м,
радиус Земли
а – большая полуось
орбиты;
М – средняя аномалия
(дуга окружности)
НА=
1068500м
Нп=
251750м
Дано:
=32˚
Е=43˚
Вычисления:
-
Большая полуось
орбиты спутника
м
-
Эксцентриситет
орбиты ИСЗ
-
Фокальный параметр
P=a∙(1-e2)=
7015644,825м
-
Радиус-вектор ИСЗ
м
м
-
Скорость ИСЗ в
перигее:
км/с
-
Скорость ИСЗ в
апогее
км/с
-
Средняя аномалия
M=E-e∙sinE=40˚43΄58.54˝
-
Период обращения
-
Определение параметров орбиты космического корабля движущегося по орбите вокруг Солнца.
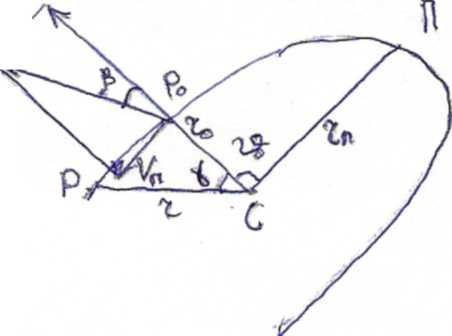
Космический корабль
совершает перелет с выключенным
двигателем в межпланетном пространстве.
Расстояния от планет таковы, что их
притяжением можно пренебречь и учитывать
только силу солнечного тяготения.
В начальный момент
времени t0,
когда корабль находился в P0
на гелиоцентрическом расстоянии
r0=1.5∙1011м,
он имел гелиоцентрическую скорость
V0=20,5
км/с, причем угол между вектором скорости
корабля и его радиус-вектором в этот
момент был равен β=50˚15΄.
Найти:
1.Истинную аномалию
корабля в начальный момент времени t0;
2.Гелиоцентрическое
расстояние rn
в момент прохождения через перигей;
3.Эксцентриситет
е и фокальный параметр P
орбиты корабля.
Решение:
Пусть k=1,32718∙1020м3/с2
– гравитационный параметр Солнца.
В момент t0
найдем:
где
откуда
Из уравнения орбиты
космического корабля получим:
С учетом этого
найдем:
1.
2.
;
3.
4.
-
Определение начальной скорости и ориентирующего угла для перехода спутника с одной орбиты на другую.
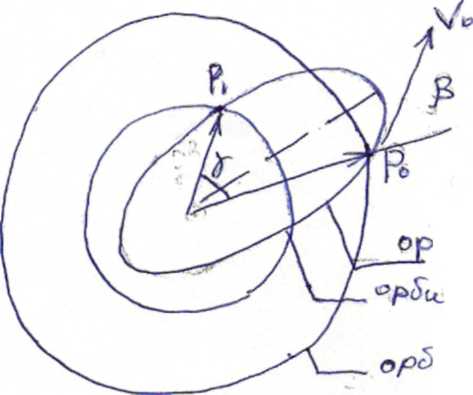
ИСЗ находится в
точке Р0
на орбите Земли (Rор
Земли =1,48∙108
км), он должен совершить перелет к орбите
Венеры и пройти через заданную точку
Р1
орбиты Венеры (Rор
Венеры = 1,08∙108
км)
Определить каким
должен быть угол β и V0min,
если γ=47˚10΄
Решение:
-
Модуль скорости
материальной точки. Движущейся по
кеплеровой орбите
где fM=1.32718∙1011
км3/с2
P=a(1-e2)
– фокальный параметр
-
Выполним
преобразование этой формулы с
использованием
а) интеграла энергии
б) интеграла площадей
в) интеграла орбиты
-
Тогда получим
следующую формулу
км/с
где
B=sin
γ=0.734322509
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
UptoLike
- « Задача 164
- Задача 166 »
40
По круговой орбите вокруг Земли обращается спутник с периодом T = 90 мин. Определить высоту спутника. Ускорение свободного падения g у поверхности Земли и ее радиус Rз считать известными.
- « Задача 164
- Задача 166 »
ОПРЕДЕЛЕНИЯ
- это универсальный коэффициент гравитационного взаимодействия, который постоянен в законе тяготения Ньютона. Он обозначается буквой G и численно равен 6,67384·10−11 (Н·м2·кг−2)
- наименьший промежуток времени, через который совершающая колебания система возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно
Дополнительные материалы
Для данной задачи нет дополнительных материалов
Похожие задачи
You should upgrade or use an alternative browser.
-
Forums
-
Homework Help
-
Introductory Physics Homework Help
Find the satellite’s altitude above the earth’s surface
-
Thread starter
whitetiger -
Start date
Nov 28, 2006 -
-
Tags -
Altitude
Surface
-
- Nov 28, 2006
- #1
Find the satellite’s altitude above the Earth’s surface.
We know that the gravitational potential energy is U = -(GMeM)/r, and it is given to be -1.49 x 10 ^11.
We also know the gravitational force to be Fg = (GMeM)/r^2
I am not sure, but can we set the two equations equal to each other and solve for r
Answers and Replies
- Nov 28, 2006
- #2
When in orbit, a communication satellite attracts the Earth with a force of 15.1 kN and the earth-satellite gravitational potential energy (relative to zero at infinite separation) is – 1.49×10^11 J. Take the radius of the Earth to be r_e = 6.38×106 m.Find the satellite’s altitude above the Earth’s surface.
We know that the gravitational potential energy is U = -(GMeM)/r, and it is given to be -1.49 x 10 ^11.
We also know the gravitational force to be Fg = (GMeM)/r^2
I am not sure, but can we set the two equations equal to each other and solve for r
Forgive me I have just started here. You might be on the right track but (and my physics is rusty) r would likely include the Earth’s radius as r should be measured from the centre of gravity.
Why not F=mg U=mgh U=Fh h=U/F
Sorry what does this (below) mean?
“”and the earth-satellite gravitational potential energy (relative to zero at infinite separation)””
i suspect this needs to be understood again as to whether the radius of Earth is included or not.
- Nov 28, 2006
- #3
Forgive me I have just started here. You might be on the right track but (and my physics is rusty) r would likely include the Earth’s radius as r should be measured from the centre of gravity.Why not F=mg U=mgh U=Fh h=U/F
Sorry what does this (below) mean?
“”and the earth-satellite gravitational potential energy (relative to zero at infinite separation)””i suspect this needs to be understood again as to whether the radius of Earth is included or not.
Yes, I have tried F=mg U=mgh U=Fh h=U/F and substituting in 1.49×10^11 J/ 15.1 kN. But I’ve got the wrong answer.
Can someone comment more on this
Thank
- Nov 28, 2006
- #4
So the above equation F = mgU = mgh U=Fh h= U/F is not correct
- Nov 29, 2006
- #5
When in orbit, a communication satellite attracts the Earth with a force of 15.1 kN and the earth-satellite gravitational potential energy (relative to zero at infinite separation) is – 1.49×10^11 J. Take the radius of the Earth to be r_e = 6.38×106 m.Find the satellite’s altitude above the Earth’s surface.
We know that the gravitational potential energy is U = -(GMeM)/r, and it is given to be -1.49 x 10 ^11.
We also know the gravitational force to be Fg = (GMeM)/r^2
I am not sure, but can we set the two equations equal to each other and solve for r
No, you can’t “set the two equations equal to each other”! They measure different things and are not equal.
Have you copied the problem correctly? You have both gravitational force and potential energy equal to -1.49 x 10^11 (one in Newtons and the other in Joules). It is possible that they happen to be the same but rather peculiar!
Assuming that is correct, you can use the fact that Fg= (GMeM)/r^2= 1.49 x 10^11 to determine that GMeM= 1.49 x 10^11 r^2. Now put that value into GMeM/r= 1.49 x 10^11 and solve for r. Hmm, you seem to have, then,
1.49 x10^11r^2/r= 1.49 x 10^11 from which we determine that r= 1 m. That satellite is “orbiting” one meter more than 10^6 m deep in the earth! Check the problem again!
Suggested for: Find the satellite’s altitude above the earth’s surface
- Mar 22, 2023
- Nov 26, 2022
- Feb 17, 2023
- Dec 21, 2021
- Mar 11, 2022
- May 7, 2023
- Dec 6, 2018
- Apr 27, 2023
- Oct 19, 2022
- Oct 25, 2020
-
Forums
-
Homework Help
-
Introductory Physics Homework Help